Binomial- und Exponentialverteilung

Fachseminar zur Stochastik
Die
Binomialverteilung
23.11.2015
Referenten: Carolin Labrzycki und Caroline Kemper
Gliederung
●
Einstieg
●
Definition der Binomialverteilung
●
Herleitung der Formel an einem Beispiel
●
Beweis
●
Beispiele
●
Zeit für Übungen
●
Approximation durch die Poisson-Verteilung
●
Zeit für Übungen
●
Ausblick
2
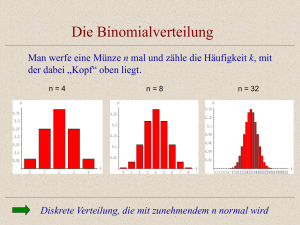
Einstieg – Das Galton-Brett
Zur Demonstration und Veranschaulichung der Binomialverteilung
entwickelte Sir Francis C. Galton (1822-1911) eine Anordnung, die man
als Galton-Brett bezeichnet. Auf einem Brett sind mehrere Nägel
befestigt, die wie gleichmäßige Dreiecke angeordnet sind und
zusammen ein gleichseitiges Dreieck bilden. Die Anordnung entspricht
einem Pascalschen Dreieck.
3
Einstieg – Das Galton-Brett
●
●
Wir wollen jetzt mit euch das Galton-Brett
simulieren!
Bitte ladet auf euer Smartphone die App: Galton
Board Simulation
4
Einstieg – Das Galton-Brett
●
Simulation auf dem Smartphone
●
●
●
●
●
●
Number of Trials: 100
Number of Trials: 500
Number of Trials: 1000
Welche Voraussetzungen sind bei dieser
Simulation gegeben?
Wie nennt man solche Experimente?
Wenn man das Experiment n-mal durchführt,
wie nennt man dieses dann?
5
Einstieg – Das Galton-Brett
●
●
Die Werte der Wahrscheinlichkeitsverteilung
ergeben sich aus den Pfadregeln: Ein Pfad mit
genau k Treffern hat nach der
Pfadmultiplikationsregel die Wahrscheinlichkeit
pk·(1-p)n-k
Zum gewünschten Ergebnis „genau k mal
Treffer“ führen alle Pfade mit genau k mal
Treffer und (n-k) mal Niete, dies entspricht (n
über k); K Kugeln auf n Plätze zu legen
6
Einstieg – Das Galton-Brett
●
●
Die Werte der Wahrscheinlichkeitsverteilung
ergeben sich aus den Pfadregeln: Ein Pfad mit
genau k Treffern hat nach der
Pfadmultiplikationsregel die Wahrscheinlichkeit
pk·(1-p)n-k
Zum gewünschten Ergebnis „genau k mal
Treffer“ führen alle Pfade mit genau k mal
Treffer und (n-k) mal Niete, dies entspricht (n
über k); K Kugeln auf n Plätze zu legen
7
Definition: Binomialverteilung
●
●
Das Galton-Brett kann man also als eine
Bernoulli-Kette der Länge n mit Parameter p
bezeichnen
Die Wahrscheinlichkeitsverteilung einer
Bernoulli-Kette der Länge n heißt
Binomialverteilung
8
Wiederholung: Binomialkoeffizient
●
●
●
●
Der Binomialkoeffizient
ist eine
mathematische Funktion, mit der sich eine
Grundaufgabe der Kombinatorik lösen lässt
Gibt an auf wie viele verschiedene Arten man k
Objekte aus einer Menge von n verschiedenen
Objekten auswählen kann
Ohne Zurücklegen, ohne Betrachtung der Reihenfolge
„49 über 6“ ist z.B die Anzahl der möglichen
Ziehungen beim Lotto (ohne Berücksichtigung der
Zusatzzahl)
9
Definition: Binomialverteilung
●
Satz: Die Wahrscheinlichkeit für genau k
Erfolge bei n unabhängigen Versuchen mit
Erfolgswahrscheinlichkeit p ist gleich
●
●
●
n= Anzahl der Versuche
p є [0,1] = Erfolgs- oder
Trefferwahrscheinlichkeit 1-p = zu p
komplementären Ausfallwahrscheinlichkeit
10
Herleitung der Formel an einem
Beispiel
●
Siehe Tafel
11
Beweis: Binomialverteilung
12
Zeit zum Üben
13
Lösungen
●
1) Ein Jäger trifft sein Ziel mit einer Wahrscheinlichkeit 40%. Mit
welcher Wahrscheinlichkeit erzielt er bei zehn Schüssen mehr
als sechs Treffer?
14
Lösungen
●
2 ) Die Wahrscheinlichkeit dafür, dass ein Bienenvolk
einen harten Winter überlebt, ist 0,4. Ein Imker besitzt 6
Völker. Wie groß ist die Wahrscheinlichkeit, dass
mindestens 2 einen harten Winter überleben?
15
Lösungen
●
3) Bei einem Automaten gewinnt man in 30% aller
Spiele. Wie groß ist die Wahrscheinlichkeit, dass man
bei 10 Spielen achtmal gewinnt?
16
Approximation durch die
Poissonverteilung
17
Approximation durch die
Poissonverteilung
●
●
●
●
Bei der praktischen Anwendung der Binomialverteilung
treten nicht selten große oder sogar sehr große Werte
von n (etwa n=10000 ) auf
Das Berechnen der Wahrscheinlichkeiten wäre dann
sehr zeitaufwendig
Deshalb versuchte man schon früh eine
Näherungsformel für die Binomialverteilung zu finden
Unter bestimmten Voraussetzungen ist es deshalb
günstig die Binomialverteilung durch die
Poissonverteilung zu approximieren
18
Approximation durch die
Poissonverteilung
●
●
●
●
Die Poissonverteilung ist eine einparametrige,
diskrete, statistische Verteilung.
Sie wird auch als „Verteilung der seltenen Ereignisse“
bezeichnet.
Die Poissonverteilung ergibt sich, wenn von einer
Binomialverteilung der Grenzwert für n gegen
unendlich und p gegen 0 gebildet wird unter
Konstanthaltung n·p (Erwartungswert λ der
Poissonverteilung)
Einziger Parameter der Poissonverteilung ist λ
(Lambda), manchmal wird für λ auch μ eingesetzt
19
Approximation durch die
Poissonverteilung
●
●
Wenn wir also große Werte von n haben, also n→∞
und kleine Werte für p, also p→0, dann wird die
Wahrscheinlichkeit für die Zufallsvariable X der
Poisson-Verteilung durch folgende Formel berechnet:
λ = ist der Erwartungswert einer binomialverteilten
Zufallsgröße (wird bei der Poisson-Verteilung auch
öfters mit dem kleinen griechischen Buchstaben μ
geschrieben und manchmal als Intensitätsparameter
bezeichnet)
●
k! ist die Fakultät der natürlichen Zahl k
●
e ist die Euler’sche Zahl (≈2,71...)
20
Approximation durch die
Poissonverteilung
●
Beispiel (Tafel):
–
Das Restaurant Fat’s Pizza führt Buch über die Anzahl an Gästen, die
das Restaurant betreten. Laut der Aufzeichnungen ist der
Erwartungswert λ = 12,1 zwischen 20:00 und 22:00 Uhr. Bestimme mit
der Poisson-Verteilung, dass die Anzahl an Gästen in Fat’s Pizza
zwischen 20:00 und 22:00 Uhr
●
genau 8 sein werden
●
höchstens 10 sein werden
●
zwischen 9 und 15 sein werden (inklusive 9 und 15)
21
Zeit zum Üben
22
Lösungen
●
4) In einer technischen Anlage sind sehr viele Module eines bestimmten
Typs verbaut. Durchschnittlich fallen 2,53 Module pro Tag aus. Die
Verteilung der Ausfälle in der Anlage kann als poissonverteilt angenommen
werden. Wie groß ist die Wahrscheinlichkeit, dass an einem Tag 3 Module
ausfallen? Das Ergebnis soll auf fünf Nachkommastellen genau angegeben
werden.
23
Lösungen
●
●
●
5) Man stelle sich den Eingang eines Kaufhauses vor, an dem ein Drehkreuz
angebracht ist, das jedes mal, wenn eine Person das Haus betritt, einen Impuls
aussendet. Langfristige Erhebungen haben gezeigt, dass durchschnittlich zwei
Kunden pro Minute eintreten. (Dabei kann es natürlich auch passieren, daß in einer
Minute niemand oder auch beispielsweise 15 Personen das Drehkreuz passieren.)
Wie hoch ist die Wahrscheinlichkeit, dass in einer Minute maximal 5 Kunden
eintreffen?
Jede mögliche Anzahl an Kunden, die innerhalb einer bestimmten Minute ankommen,
besitzt eine gewisse Wahrscheinlichkeit.Der Erwartungswert der Anzahl an Kunden,
die pro Minute eintreffen, beträgt . Wir haben also einen Poisson-Prozeß mit der
Intensität 2.
Die gesuchte Wahrscheinlichkeit beträgt also 0.9834342; es werden also mit sehr
hoher Wahrscheinlichkeit (in über 98 von 100 Fällen) maximal 5 Leute pro Minute
ankommen.
24
Zusammenfassung
●
Faustregel Binomialverteilung
–
Gegeben sei eine Situation, bei der
1. etwas gezählt und
2. bei der man das Ergebnis als unabhängige Überlagerung von sehr vielen BernoulliExperimenten interpretieren kann
–
●
dann kann man die Wahrscheinlichkeitsverteilung mit der
Binomialverteilung ausrechnen!
Faustregel Poissonverteilung
–
Gegeben sei eine Situation, bei der
1. etwas gezählt und
2. bei der man das Ergebnis als unabhängige Überlagerung von sehr vielen BernoulliExperimenten mit sehr kleiner Wahrscheinlichkeit und großen n interpretieren kann
–
Dann sagt das vorstehende Ergebnis, dass die fraglichen
Wahrscheinlichkeiten poissonverteilt zu einem Parameter λ
(Erwartungswert) sind.
25
Ausblick
●
Nächste Woche werden wir uns mit dem Thema
Exponentialverteilung beschäftigen!
Vielen Dank für Eure
Aufmerksamkeit!
26
Fachseminar zur Stochastik
Die
Exponentialverteilung
30.11.2015
Referenten: Carolin Labrzycki und Caroline Kemper
27
Gliederung
●
Einstieg
●
Gedächtnislose Wartezeiten
●
Definition
●
Satz
●
Faustregel
●
Beispiel
●
Zeit zum Üben
28
Einstieg
●
●
Es gibt zahlreiche Beispiele im täglichen Leben, in
denen wir auf etwas warten
–
Auf den nächsten Regen
–
Auf die nächste Uni-Linie
–
Darauf, dass das Telefon der Freundin nicht mehr
besetzt ist
Doch der Charakter des Wartens kann ganz
unterschiedlich sein:
29
Beispiel 1
Der zuverlässige Handwerker
Er hat zugesagt, irgendwann zwischen 5 und 6 Uhr zu
kommen. Um 5 Uhr erwarten wir ihn gleichverteilt
innerhalb der nächsten Stunde, wir kalkulieren eine
mittlere Wartezeit von 30 Minuten ein. Wenn er um
5.30 Uhr noch nicht da ist, schrumpft der
Erwartungswert der Wartezeit auf 15 Minuten.
Kurz: Die Zeitspanne, die wir schon gewartet haben,
verändert die Erwartung für das zukünftige Warten.
30
Beispiel 2
Die besetzte Telefonleitung
Sie rufen bei Ihrer Bank (oder Krankenkasse, Finanzamt, …) an,
es ist besetzt. Im Mittel wird die Leitung nach drei Minuten frei
sein, aber im Einzelfall kann man es nie genau wissen. Je
nachdem, wie aufwändig die Beratung im Einzelfall ist, kann es
auf unvorhersehbare Weise schneller oder langsamer gehen.
Kurz: Auch wenn man schon eine Weile gewartet hat,
verändert das die Prognose für die noch zu erwartende
Wartezeit nicht.
31
●
●
Die zugehörigen Wahrscheinlichkeiten können
sehr unterschiedlich sein
Eine besondere Rolle spielen Wartezeiten, bei
denen man nie genau weiß, wie lange es noch
dauern wird
32
●
●
Jede auf irgendeinem Wahrscheinlichkeitsraum
definierte Zufallsvariable T :   0,
kann als Wartezeit interpretiert werden
33
Gedächtnislose Wartezeiten
34
Definition : Gedächtnislose
Wartezeiten
Es sei T eine Wartezeit, d.h. T :   0, Ist eine
beliebige Zufallsvariable. Wir sagen, dass T
gedächtnislos ist, wenn
ℙ= T  t   ℙ ({T  s  t} | {T  s})
für beliebiges s, t  0 gilt.
1 n
● Die Folge (a )mit an  (1 
) ist konvergent.
n
n
●
●
Aufgabe: Bildet den Grenzwert für die Folge
Was fällt auf?
1 n
an  lim(1  )
n
n
Grenzwert
1 n
(
1

)
n
n
1 2
2 2,25
3 2,37037…
…
100
1.000
10.000
100.000
1.000.000
10.000.000
100.000.000
2,7048…
2,7169…
2,71814…
2,718268…
2,718280…
2,718281…
2,718281..
Ihr Grenzwert ist eine irrationale Zahl und heißt eulersche Zahl e. Es ist e  2,718281828459… .
Satz
1 n
● Satz: Die Folge (a ) mit
an  (1  )
n
n
ist konvergent. Ihr Grenzwert ist eine irrationale
Zahl und heißt eulersche Zahl e. Es ist e ≈
2,71828...
Satz:
1 n
Die Folge (an ) mit an  (1  n ) ist konvergent. Ihr
Grenzwert ist eine irrationale Zahl und heißt
eulersche Zahl e. Es ist e 2,71828…
Alle Ereignisse ��∊ ℝ
x n
e  lim (1  )
n 
n
x
Die e-Funktion
●
Funktion: f ( x)  e
●
x
f
'
(
x
)

e
1. Ableitung:
●
Stammfunktion: F ( x)  e
a
●
Integral: 
b
x
x
b
 
f ( x)dx  e x
a
 eb  e a
Satz
●
Satz:
–
(i) Es sei T eine Wartezeit für die ℙ T exponentialverteilt zu
irgendeinem Parameter λ>0 ist. Dann ist T gedächtnislos.
–
(ii) Sei umgekehrt T eine gedächtnislose Wartezeit. Wir
setzen voraus, dass T im folgenden Sinn nichttrivial ist: Es
gibt ein t0>0 mit ℙ ({T0  t0 })  0
–
T ist also nicht die Wartezeit, bei der {T=0}
Wahrscheinlichkeit Eins hat
–
–
Dann gibt es ein λ>0, so dass ℙT exponentialverteilt zum
Parameter λ ist:
Es ist ℙ ({a  T
b
 b})    e  x dx
a
Faustregel zum Arbeiten mit
gedächtnislosen Wartezeiten
Angenommen, es geht um eine Wartezeit T, und
aus irgendwelchen Gründen ist es plausibel
anzunehmen, dass sie gedächtnislos ist
(Beratung, besetztes Telefon usw.)
Wenn dann T im Mittel der Wert µ hat, so kann T
durch eine Exponentialverteilung mit Parameter
1 modelliert werden.
 :

Faustregel zum Arbeiten mit
gedächtnislosen Wartezeiten
Angenommen, es geht um eine Wartezeit T, und
aus irgendwelchen Gründen ist es plausibel
anzunehmen, dass sie gedächtnislos ist
(Beratung, besetztes Telefon usw.)
Wenn dann T im Mittel der Wert µ hat, so kann T
durch eine Exponentialverteilung mit Parameter
1 modelliert werden.
 :

Beispiel
Wenn Sie bei Ihrer besten Freundin / Freund anrufen, ist es oft besetzt,
und im Mittel dauert es 20 Minuten, bis der Anschluss wieder frei ist.
Solche Situationen, bei denen es „ungewiss lange“ dauert, können gut
durch gedächtnislose Wartezeiten modelliert werden. Aufgrund der
vorstehenden Faustregel kann man zur Modellierung eine
Exponentialverteilung mit dem Parameter  : 1 wählen.
20
Und nun können alle interessierenden Wahrscheinlichkeiten berechnet
werden.
Wie wahrscheinlich ist es zum Beispiel, dass die Leitung schon in 10
Minuten wieder frei ist?
Die Lösung: siehe Tafel
Zeit zum Üben
Lösungen
1.
F ( x)  1  e
1
   0,2
5
x  10
  x
F (10)  1  e
 0 , 210
 0,8647
Lösungen
2. F ( x)  1  e
 x
1

6
x  10
F (10)  1  (1  e
●
1
 10
6
)e

10
6
 0,1889
Die Verteilungsfunktion der Exponentialverteilung ist hier anzuwenden. Diese gibt die
Wahrscheinlichkeit an, dass eine Zeitlücke „kleiner gleich x“ auftritt. Deshalb muss
über 1-F(x) die Gegenwahrscheinlichkeit gebildet werden. Die Parameter λ ist der
Kehrwert des Mittelwertes.
Lösungen
3.
 x
F ( x)  1  e
1
   0,1
10
x 8
F (8)  1  e
 0 ,18
 0,5507
Vielen Dank für Eure
Aufmerksamkeit!