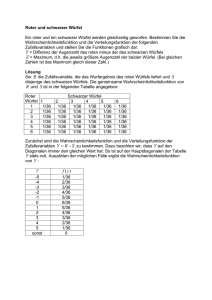
Zuverlässigkeitstheorie
Werbung

Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Zuverlässigkeitstheorie 3. Grundbegriffe der Wahrscheinlichkeitsrechnung Prof. Jochen Seitz Fachgebiet Kommunikationsnetze“ ” 20. November 2008 Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Übersicht 1 Gesetz der großen Zahlen von Bernoulli 2 Erste Grundlagen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit 3 Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Binomialverteilung Poisson-Verteilung Normalverteilung Exponentialverteilung Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Gesetz der großen Zahlen von Bernoulli Sei A ein zufälliges Ereignis, das im Ergebnis eines Zufallsexperiments auftreten kann oder nicht. Dieses Experiment werde unter konstanten Bedingungen n-fach durchgeführt. Dabei sei mit n(A) die absolute Häufigkeit des Eintretens des Ereignisses A bezeichnet, mit p(A) = n(A)/n die relative Häufigkeit. Sei p die Wahrscheinlichkeit für das Eintreten von A, dann gilt: Gesetz der großen Zahlen von Bernoulli Für eine beliebig kleine Zahl gibt es eine Experimentanzahl n, so dass mit beliebig nahe bei 1 liegender Wahrscheinlichkeit die relative Wahrscheinlichkeit p(A) nicht weiter als um von p abweicht. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Interpretation Interpretation Bei genügend großer Anzahl von Versuchen einer zufälligen Ereignisses lässt sich die Wahrscheinlichkeit für dessen Auftreten beliebig genau bestimmen. Bedeutung der Wahrscheinlichkeit Die Natur der Wahrscheinlichkeit ist derart, dass sie erlaubt, ziemlich genau (und nicht exakt) die Anzahl gewisser Ereignisse bei einer großen Zahl von Versuchen vorherzusagen. Der Ausgang eines einzelnen Versuchs kann jedoch nicht vorhergesagt werden, lediglich die Wahrscheinlichkeit des Eintretens eines besttimmten Ereignisses bei einem Einzelexperiment kann genau abgeschätzt werden. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Interpretation für technische Systeme Interpretation der Zuverlässigkeit technischer Systeme Es kann niemals exakt vorausgesagt werden, ob eine betrachtete technische Einheit einen vorgegebenen Zeitraum überlebt (oder nicht überlebt). Allerdings ist die Angabe einer Wahrscheinlichkeit für das Überleben (oder Ausfallen) der Einheit möglich. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Wahrscheinlichkeit beim Würfeln Man würfle n-mal. Die Ergebnisse sind Ai = i für i = 1, 2, 3, 4, 5, 6. Jedes Ergebnis Ai trat mit der Häufigkeit ni auf. Für jedes Ergebnis Ai kann eine relative Häufigkeit hn (Ai ) = nni angegeben werden. ni n→∞ n Es gilt lim hn (Ai ) = lim n→∞ = P(Ai ) P(Ai ) ist die Wahrscheinlichkeit für das Auftreten von Ai . Aus 0 ≤ ni ≤ n folgt 0 ≤ P(Ai ) ≤ 1. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Allgemeines In der Praxis sind Wahrscheinlichkeiten meist relative Häufigkeiten: Zahl der günstigen Ausgänge Wahrscheinlichkeit = Zahl der möglichen Ausgänge Die Wahrscheinlichkeit des unmöglichen Ereignisses: P(unmöglich) = 0 oder P(O) = 0 Die Wahrscheinlichkeit des sicheren Ereignisses: P(sicher) = 1 oder P(E ) = 1 Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Ereignisse A und Ā Sei das Auftreten eines bestimmten Ereignisses mit A beschrieben und daher das nicht-Auftreten desselben Ereignisses mit Ā. Dann gilt für die Auftretenswahrscheinlichkeiten: PA + PĀ = 1 PĀ = 1 − PA P(A∪Ā) = 1 = PA + PĀ Prof. J. Seitz Zuverlässigkeitstheorie (1) (2) (3) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Verbundwahrscheinlichkeiten sich ausschließender Ereignisse Allgemein gilt für die Verbundwahrscheinlichkeit sich gegenseitig ausschließender Ereignisse A1 , A2 : P(A1 ∪A2 ) = PA1 + PA2 (4) oder allgemein für n sich gegenseitig ausschließende Ereignisse: P(A1 ∪A2 ∪A3 ∪···∪An ) = n X PAi i=1 Prof. J. Seitz Zuverlässigkeitstheorie (5) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Verbundwahrscheinlichkeiten sich nicht ausschließender Ereignisse Für beliebige Ereignisse A und B, die sich nicht ausschließen, gilt: P(A∪B) = PA + PB − P(A∩B) (6) Dies ist verträglich zu Gleichung 4, da bei sich gegenseitig ausschließenden Ereignissen A und B die Wahrscheinlichkeit, dass beide gleichzeitig auftreten, gleich 0 ist, d. h. P(A∩B) = 0 Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Beispiel Kartenspiel – I Gegeben sei ein Kartenspiel mit 52 Karten. Gesucht sei die Wahrscheinlichkeit, dass beim Kartenziehen ein König gezogen wird (PK ). Lösung: PK = PKkreuz + PKpik + PKherz + PKkaro 1 1 1 1 + + + 52 52 52 52 = Prof. J. Seitz Zuverlässigkeitstheorie = 1 13 Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Beispiel Kartenspiel – II Gegeben sei ein Kartenspiel mit 52 Karten. Gesucht sei nun die Wahrscheinlichkeit, dass eine Herz-Karte oder eine 4 gezogen wird. Lösung: Sei PHerz die Wahrscheinlichkeit, dass eine Herz-Karte gezogen wird, und P4 die Wahrscheinlichkeit, dass eine 4 gezogen wird. Diese Ereignisse schließen sich nicht aus, da das Ereignis “eine Herz-4 wurde gezogen” in beiden Ereignissen enthalten ist! Daher muss wie folgt vorgegangen werden: Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Beispiel Kartenspiel – III 1 PHerz = 2 P4 = 1 13 3 PHerz 4 1 4 → es gibt vier Farben; → es gibt vier Karten mit 4; = 1 52 → genau die Herz-4 wird gezogen. Aus Gleichung 6 folgt: Prot∪4 = PHerz + P4 − PHerz 1 1 1 + − = 4 13 52 4 = 13 Prof. J. Seitz Zuverlässigkeitstheorie 4 Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Bedingte Wahrscheinlichkeit Die bedingte Wahrscheinlichkeit hat große Bedeutung in der Zuverlässigkeitstheorie. Es gilt: PA∩B = PB ∗ PA/B (7) PA∩B = PA ∗ PB/A PA∩B = PB PA∩B = PA (8) PA/B PB/A Prof. J. Seitz Zuverlässigkeitstheorie (9) (10) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Bedingte Wahrscheinlichkeit bei einem Kartenspiel – I Gesucht: Die Wahrscheinlichkeit, dass eine gezogene Karte die Herz-5 ist, wenn bereits bekannt ist, dass die gezogene Karte eine Herz-Karte ist. Sei dafür A das Ereignis, dass eine Herz-5 gezogen wurde und B das Ereignis, dass eine Herz-Karte gezogen wurde. Gesucht ist somit PA/B . Lösung: Es gilt 1 PA = 52 ; 1 PB = 4 ; 1 PA∩B = 52 (= PA ). Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Bedingte Wahrscheinlichkeit bei einem Kartenspiel – II Somit ist PA/B = = Prof. J. Seitz PA∩B PB PA PB = 1 52 1 4 = 1 13 Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeit als relative Häufigkeit Verbundwahrscheinlichkeiten Bedingte Wahrscheinlichkeit Bedingte Wahrscheinlichkeit bei unabhängigen Ereignissen Wenn die Ereignisse unabhängig sind, d.h. wenn gilt PA/B = PA (Interpretation: Die Auftretenswahrscheinlichkeit von A ist unabhängig davon, ob B aufgetreten ist) gilt für die Wahrscheinlichkeit für das gemeinsame Auftreten dieser Ereignisse: n Y PA1 ∩A2 ∩A3 ∩···∩An = PAi (11) i=1 Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Zufallsvariablen Zufallsvariablen, die interessierende Beobachtungsgegenstände beschreiben, können kontinuierlich oder diskret sein: Zufallsvariablen sind diskret, wenn ein zufälliges Ereignis endlich viele oder abzählbar unendlich viele Werte annehmen kann. Beispiele sind somit das Auftreten einer bestimmten Karte in einem Kartenspiel, das Erscheinen einer bestimmten Zahl bei einem Würfelspiel oder die Anzahl von defekten respektive funktionierenden Einheiten eines Ensembles. Bei stetigen Zufallsvariablen ist die Menge der möglichen Ereignisse nicht abzählbar. Hierzu können beispielhaft Zeit, Temperatur, Spannung u.s.w. genannt werden. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Beispiel: Würfeln – I Prinzipiell kann es beim Würfeln mit genau einem Würfel sechs mögliche Ereignisse geben. Der Ereignisvektor ist somit E = [x1 , x2 , x3 , x4 , x5 , x6 ] = [1, 2, 3, 4, 5, 6]. Die Wahrscheinlichkeitsdichte f (x) ist dann die Zuordnung genau eines Wahrscheinlichkeitswertes zu jedem möglichen Ereignis, d.h. zu jedem Element des Ereignisvektors: P(X = xi ) = P(xi ) = f (xi ) (12) Da die xi den gesamten Ereignisraum bilden, es also keine anderen Ereignisse geben kann, gilt immer: X P(xi ) = 1 (13) ∀i Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Beispiel: Würfeln – II Für das Beispiel des Würfelns ergibt sich 1 f (xi ) = 6 Das Auftreten der einzelnen Zahlen ist also gleich wahrscheinlich. Über die angegebene Bedingung X X P(xi ) = f (xi ) ∀i ∀i = X1 ∀i 6 1 =1 6 kann man auch die Plausibilität dieser Funktion überprüfen. = 6∗ Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Verteilungsfunktion Die Verteilungsfunktion gibt dann an, wie wahrscheinlich es ist, dass ein Ereignis innerhalb eines bestimmten Bereiches eintritt. Sie wird auf der Basis der Wahrscheinlichkeitsdichte definiert als F (xi ) = P(X ≤ xi ) X = f (xi ) (14) (15) X ≤xi Eine Verteilungsfunktion ist somit monoton wachsend und hat als Grenzwerte 0 und 1. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion beim Würfeln f(x) 1 F(x) 1/6 x 1 2 3 4 5 6 Prof. J. Seitz x 1 2 3 Zuverlässigkeitstheorie 4 5 6 Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Stetige Zufallsvariablen Betrachtet man nun Wahrscheinlichkeitsdichte und -verteilung einer stetigen Zufallsvariablen, so ist offensichtlich, dass diese ebenfalls stetig sind. Die Wahrscheinlichkeitsverteilung gibt dabei wiederum an, mit welcher Wahrscheinlichkeit ein zufälliger Wert eines Vorganges kleiner als das übergebene Argument x ist: F (x) = P(X ≤ x). Die Wahrscheinlichkeitsdichte ergibt sich aus f (x) = F 0 (x): Zk F (k) = P(X ≤ k) = f (y ) dy (16) −∞ F (−∞) = 0 (17) F (∞) = 1 (18) Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Beispiel für stetige Zufallsvariablen I Ein elektrisches Signal hat eine zufällige Spannung X im Bereich zwischen 0 und 1 V. Die Auftretenswahrscheinlichkeit ist im angegebenen Intervall gleich. Damit ergibt sich folgende Wahrscheinlichkeitsdichte: Die Fläche unter der Wahrscheinlichkeitsdichtefunktion ist gleich 1. Die Wahrscheinlichkeit für das Auftreten einer Spannung genau x ist gleich 0, da der Vorrat an möglichen Werten unendlich groß ist. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Beispiel für stetige Zufallsvariablen II Für stetige Zufallsvariablen ist die Wahrscheinlichkeit dafür, dass genau ein Wert auftritt, immer gleich 0. Es kann lediglich eine Wahrscheinlichkeit dafür angegeben werden, dass ein gemessener oder anders ermittelter Wert in einem spezifizierten Intervall liegt. Diese Wahrscheinlichkeit ergibt sich aus Zx2 P(x1 < X ≤ x2 ) = f (x) dx (19) x1 Wichtig Mit der Dichte- oder Verteilungsfunktion einer Zufallsvariablen ist damit deren vollständige Beschreibung möglich. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Wichtige Werte Oftmals sind Aussagen über das mittlere Gesamtverhalten einer Zufallsvariablen ausreichend. Die wichtigsten Aussagen, die über eine Zufallsvariable getroffen werden können, sind deren Mittelwert oder Erwartungswert; deren quadratischer Mittelwert; deren mittlere quadratische Abweichung Diese werden im Folgenden kurz behandelt. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen (Linearer) Mittelwert einer diskreten Zufallsvariablen Der Mittelwert einer diskreten Zufallsvariablen berechnet sich aus m1 = = = = = m E [X ] x̄ P xi ∗Ni ∀xi P N P(xi ) ∗ xi ∀xi Prof. J. Seitz Zuverlässigkeitstheorie (20) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen (Linearer) Mittelwert einer stetigen Zufallsvariablen Für stetige Zufallsvariablen gilt: Z∞ x ∗ f (x) dx m= −∞ Prof. J. Seitz Zuverlässigkeitstheorie (21) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Beispiel: Dreiecksverteilung I Diese ensteht bei der Summe von zwei unabhängigen, gleichverteilten R(0, 1) Zufallsvariablen [1]. Die Wahscheinlichkeitsdichte ist somit gegeben durch 0≤x <1 x, 2 − x, 1 ≤ x < 2 f (x) = 0, sonst (22) Die Verteilungsfunktion errechnet sich durch Integration, die der Übung überlassen bleibt. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Beispiel: Dreiecksverteilung II 1.2 f(x) 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -1 -0.5 0 0.5 Prof. J. Seitz 1 1.5 2 Zuverlässigkeitstheorie 2.5 3 Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Quadratischer Mittelwert Der quadratische Mittelwert gibt darüber Auskunft, wie stark die Zufallsvariable um den Wert 0 streut. Für diskrete Zufallsvariablen gilt: X m2 = E [x 2 ] = P(xi ) ∗ xi2 (23) ∀xi Der quadratische Mittelwert für stetige Zufallsvariablen dagegen berechnet sich aus Z∞ m2 = x 2 ∗ f (x) dx −∞ Prof. J. Seitz Zuverlässigkeitstheorie (24) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Mittlere quadratische Abweichung Die mittlere quadratische Abweichung, auch Zentralmoment zweiter Ordnung oder Varianz genannt, ist ein Maß dafür, wie stark eine Zufallsvariable um ihren Mittelwert streut. Im Fall einer diskreten Zufallsvariablen ergibt sich die Varianz wie folgt: X µ2 = E [(x − x̄)2 ] = (xi − x̄)2 ∗ P(xi ) (25) ∀xi Bei stetigen Zufallsvariablen gilt dann allgemein: Z∞ µ2 = (x − x̄)2 ∗ f (x) dx −∞ Prof. J. Seitz Zuverlässigkeitstheorie (26) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Zusammenhang Der Zusammenhang zwischen linearem, quadratischem Mittelwert und der mittleren quadratischen Abweichung lässt sich einfach herleiten: µ2 = m2 − m12 Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Bernoulli-Experiment Interessiert bei einem Versuch lediglich das Auftreten eines gegebenen Ereignisses A oder ¬A, so kann das Versuchsergebnis durch eine Zufallsvariable X beschrieben werden, die nur zwei Werte annimmt: X = 1, wenn das Ereignis A eintritt X = 0, wenn A nicht eintritt. Die Wahrscheinlichkeit, dass das Ereignis A eintritt, sei mit p gegeben. Daraus lassen sich ableiten: E [X ] = 1 ∗ p + 0 ∗ (1 − p) = p 2 2 2 E [X ] = 1 ∗ p + 0 ∗ (1 − p) = p 2 2 Var [X ] = E [X ] − E [X ] 2 2 = 1 ∗ p − p = p ∗ (1 − p) Prof. J. Seitz Zuverlässigkeitstheorie (27) (28) (29) (30) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Binomialverteilung Für die Wahrscheinlichkeit, dass das Ereignis A bei n Versuchen genau k-mal auftritt, gilt dann die Binomialverteilung: n Pk (X = k) = p k (1 − p)n−k (31) k Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Binomialverteilung – Erklärung Auf diese Formel kommt man ganz anschaulich, indem man sich die möglichen Kombinationen betrachtet, die zum gewünschten Ereignis führen. Eine Möglichkeit ergibt sich daraus, dass die ersten k Versuche bereits A als Resultat haben. Dann müssen die restlichen (n − k) Versuche ¬A zum Ergebnis haben. Die Wahrscheinlichkeit hierfür ist p k (1 − p)n−k , da die einzelnen Versuche unabhängig voneinander sind. n Insgesamt gibt es unabhängige Kombinationen. k Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Verteilungsfunktion der Binomialverteilung Für die Verteilungsfunktion gilt dann x X n F (x) = P(X ≤ x) = p i (1 − p)n−i i i=0 Prof. J. Seitz Zuverlässigkeitstheorie (32) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Poisson-Verteilung Die Poisson-Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die beim mehrmaligen Durchführen eines Bernoulli-Experiments entsteht. Führt man ein solches Experiment sehr oft durch und ist die Erfolgswahrscheinlichkeit gering, so ist die Poisson-Verteilung eine gute Näherung für die entsprechende Wahrscheinlichkeitsverteilung. Sie gibt somit an, mit welcher Wahrscheinlichkeit eine bestimmte Anzahl statistisch unabhängiger Ereignisse auftritt. Die Abstände, in denen die Ereignisse eintreten, sind dabei exponentiell verteilt. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Mathematische Beschreibung der Poisson-Verteilung Verteilungsdichte der Poisson-Verteilung: f (k) = Pλ (X = k) λk −λ e = k! (33) (34) Verteilungsfunktion der Poisson-Verteilung F (k) = Pλ (X ≤ k) = k X i=0 Prof. J. Seitz λi −λ e i! Zuverlässigkeitstheorie (35) (36) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Poisson-Verteilung mit λ = 6 Quelle: http://de.wikipedia.org/w/index.php?title=Bild: Poisson-lambda6.png&filetimestamp=20050723201419 Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Normalverteilung Viele quantitative Größen konzentrieren sich oft um einen bestimmten Wert und größere Abweichungen sind eher selten. ⇒ Glockenkurve Normalverteilung dient als Approximation eines solchen Verhaltens. Unter bestimmten Voraussetzungen kann man auch theoretisch zeigen, dass die Verteilung einer Summe von unabhängigen “ Zufallsvariablen gegen die Normalverteilung ” strebt. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Dichte der Normalverteilung Die Dichte der Normalverteilung – bezeichnet mit N(µ, σ 2 ) – ist gegeben durch f (x) = √ (x−µ)2 1 e − 2σ2 , µ, x ∈ (−∞, ∞), σ > 0 2πσ wobei µ einen Ortsparameter (das Mittel) und σ einen Skalierungsparameter darstellen [2]. Prof. J. Seitz Zuverlässigkeitstheorie (37) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Dichte der Normalverteilung Quelle: http://de.wikipedia.org/w/index.php?title=Bild: Normal_density.svg&filetimestamp=20080316210707 Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Verteilungsfunktion der Normalverteilung Die Verteilungsfunktion ist natürlich das Integral über f , d. h. Zx F (x) = Zx f (t)dt = −∞ −∞ √ (t−µ)2 1 e − 2σ2 dt 2πσ Ihre Berechnung ist nicht ganz einfach, entsprechende Werte werden üblicherweise Tabellen entnommen. Prof. J. Seitz Zuverlässigkeitstheorie (38) Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Standard-Normalverteilung I Betrachten wir nun die transformierte Zufallsvariable Z = X σ−µ , wobei X N(µ, σ 2 ) verteilt ist. Die Verteilungsfunktion G(z) wird zu G (z) = P(Z ≤ z) X −µ = P( ≤ z) σ = P(X ≤ zσ + µ) = F (zσ + µ) zσ+µ Z (t−µ)2 1 √ = e − 2σ2 dt 2πσ −∞ Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Standard-Normalverteilung II Die Transformation der Integrationsvariablen t → zσ + µ liefert Zz G (z) = −∞ Zz = t2 1 √ e − 2 dt 2π g (t)dt −∞ Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Standard-Normalverteilung III G und g werden dann Verteilungsfunktion bzw. Dichtefunktion der Standard-Normalverteilung N(0,1) genannt, die manchmal auch mit Φ respektive φ bezeichnet werden. Die Verteilung heißt auch Gauß’sch. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Beispiel I Ein Psychologe benutzt ein Instrument, das ihm Werte liefert, die N(500, 10.000) verteilt sind. Gesucht ist die Wahrscheinlichkeit, dass ein Wert kleiner oder gleich 600 ist. 600 − 500 X − 500 ≤ ) 100 100 = P(Z ≤ 1) P(X ≤ 600) = P( = G (1) = 0.8413 Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Beispiel II Wie groß ist die Schranke, unter der ein Wert mit 95% Wahrscheinlichkeit liegt? 0.95 = P(X ≤ x) x − 500 X − 500 ≤ ) = P( 100 100 x − 500 = G( ) 100 Aus der Tabelle folgt x = 664 ergibt. x−500 100 = 1.64, woraus sich die Schranke Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Exponentialfunktion Die Exponentialverteilung hat die Dichtefunktion f (t) = λe −λt , t ≥ 0, λ > 0 (39) und die Verteilungsfunktion F (t) = 1 − e −λt , t ≥ 0, λ > 0 (40) Diese Verteilung wird im weiteren Verlauf der Vorlesung mit anderen wichtigen Verteilungen zur Modellierung des Zuverlässigkeitsverhaltens genauer behandelt. Prof. J. Seitz Zuverlässigkeitstheorie Gesetz der großen Zahlen von Bernoulli Erste Grundlagen Diskrete und kontinuierliche Zufallsvariablen Wahrscheinlichkeitsdichte und Verteilungsfunktion Mittelwerte von Zufallsvariablen Beispiele für Verteilungen diskreter und stetiger Zufallsvariablen Literatur R. Dutter, “Einführung in die wahrscheinlichkeitsrechnung und statistik (für informatiker).” http: //pc2.statistik.tuwien.ac.at/public/dutt/inf/, Sommersemester 1998/99. Skriptum zur Vorlesung an der Technischen Universität Wien. W. Gromes, “Mathematik für biologen und humanbiologen.” http://www.mathematik.uni-marburg.de/~gromes/ biologen.html, Wintersemester 2000/2001. Skript zur Vorlesung an der Universität Marburg. Prof. J. Seitz Zuverlässigkeitstheorie