K - Unibas Chemie

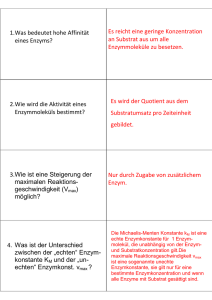
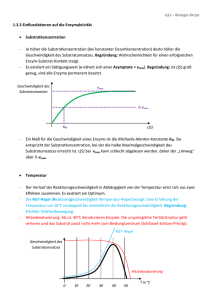
Die Kinetik zusammengesetzter Reaktionen
o Beispiele von zusammengesetzter Reaktionen
o Homogene Catalyse: Merkmale homogen-catalysierter Reaktionen
o Enzymcatalysierte Reaktionen
 P. Atkins, J. de Paula, “Physikalische Chemie”, Wiley-VCH Verlag GmbH&
Co, 2006, 23.3.
 G. Wedler, H-J. Freund, „Lehrbuch der Physikalischen Chemie“, Wiley-VCH
Verlag GmbH& Co, 2010, 6.7.2
Bilder in Skripts: von P. Atkins, J. de Paula, “Physikalische Chemie”, Wiley-VCH Verlag
GmbH& Co, 2006, 23.3
Beispiele von zusammengesetzter Reaktionen
 Kettenreaktionen ( Gasphasenreaktionen)
 Polymerisationen (Kettenreaktionan in flüssiger Phase)
 Homogene Catalyse
 Photochemische Reaktionen
Kettenreaktionen = bei einer Reaktion ensteht in einem Schritt ein
Zwischenprodukt,
welches
weiterreagiert, und so weiter.
zu
einem
nächsten
Zwischenprodukt
Wird in PC-II erklärt
Catalyse = chemische Reaktion mit Hilfe von Katalysatoren ausgeführt
-Homogene Catalyse
- Heterogene Catalyse
Katalysatoren
Katalysator
 eine Reaktion beschleunigt, ohne dass sie
(Netto)reaktion eingeht.
setz die Aktivierungenergie einer Reaktion herab
selbst
Die Wirkungsweise eines Katalysators beruht
auf seiner Möglichkeit, den Mechanismus einer
chemischen Reaktion derart zu verändern:
Einen alternativen Reaktionweg → umgeht den
langsamen,
geschwindigkeitsbestimmenden
Schritt der unkatalisierten Reaktion.
Homogener
Katalyator
=
befindet sich in der gleichen
Phase wie die Reaktionsmischung
Heterogener Katalysator =
befindet sich in einer anderen Phase wie
die Reaktionsmischung (z.B. fester
Katalysator in Gasphasenreaktion :
Hydrierung von Ethen → Ethan - man
verwendet Pt, Ni, Pd)
Katalysatoren: Beispiele (1 & 2)
Beispiel 1:
Enzyme: biologische Katalisatoren → hochspezifisch → können die
Geschwindigkeit der Reaktion dramatisch steigen
 die Aktivierungsenergie der Zersetzung von H2O2 in Lösung → 76 KJmol-1
 die Aktivierungsenergie der Zersetzung von H2O2 durch I- → 57 KJmol-1
↓
2000 x schneller !
 die Aktivierungsenergie der Zersetzung von H2O2 durch Ensyme → 8 KJmol-1
Beispiel 2:
↓
1015 x schneller (295ºK) !
 die Aktivierungsenergie der Zersetzung von Rohrzucker (Hydrolyse) → 107 kJ/mol
 die Aktivierungsenergie der Zersetzung von Rohrzucker durch Saccharase → 36 KJmol-1
↓
1012 x schneller (310ºK) !
Katalysatoren: Beispiele (3)
Mettale: Platin, Rhodium, Palladium, Braunstein katalysieren die Hydrierung
und Dehydrierung von Ethanol.
Mettaloxiden
katalysieren
ie Oxidation
von Kohlenstoffmonoxid
zu
Kohlenstoffdioxid bei T =25 C.
Fahrzeugkatalysator: Aufgabe des Fahrzeugkatalysators ist die chemische
Umwandlung der Verbrennungsschadstoffe
Kohlenwasserstoffe (CmHn),
Kohlenstoffmonixid (CO), und Stickoxide (NO2) ) in Wasser (H2O) und
Stzickstoff (N2) durch Oxidation beziehungweise Reduktion.
Der Fahrzeugkatalysator = besteht meistens aus mehreren Komponenten.
Die Kinetik zusammengesetzter Reaktionen
Katalisyerte Reaktion:
- Reaktanten A und B
- eines oder mehrerer Produkte P
k1
A+B+K
k1‘
k2
A·K + B
A·B·K
P+K
k2‘
Der Katalysator fällt aus der summarische Reaktionsgleicheung
heraus → ∆Gº : identisch für die nichtkatalysierte und katalisyerte
Reaktion
∆Gºkat = ∆Gºnichtkat
Das Thermodynanische Gleichgewicht
Das TD Gleichgewicht zwischen A und B und P (Ps) kann nicht beeinflusst
werden durch die Verwendung eines Katalysators
- eine TD nicht mögliche Reaktion kann durch die Anwendung eines
Katalysators nicht erzwungen werden !!!
Ein Katalysator hat nur Einfluss auf die Reaktionsgeschwindigkeit (V) !
Selektivität des Katalysators → der eine oder der andere Reaktionsweg
durch einen speziellen Katalysator begünstig (stark beschleunigt) wird
Merkmale homogen-katalysierter Reaktionen
Funktionsprinzip eines homogenen Katalysators:
z.Beispiel:
Br-Katalysierten Zersetzung von H2O2
2 H2O2 (aq) → 2 H2O (aq) + O2
- das folgende Gleichgewicht:
(a)
H3O+ + H2O2
H3O2+ + H2O
Aktivität H2O → 1

HO 
K
H O H O 
3

2

2
2
3
TD Eigenschaften der anderen beteiligten Substanzen → Ideal
(b)
H3O2+ + Br-
→ HOBr + H2O

Ist geschwindigkeitsbestimmend
(c)
HOBr + H2O2 → H3O+ + O2 + Br-
 
v  k H 3O2 Br 
(schnell)
Br-katalysierten Zersetzung von H2O2
Funktionsprinzip eines homogenen Katalysators:
- Geschwindigkeit der Gesamtreaktion → Geschwindigkeit des Schrittes (b)
- Konzentration des H3O2+ = f(Geschwindigkeitskonstante , Ausgangstoffe)
d O2 
 K eff H 2O2  H 3O  Br 
dt


 

 
v  k H 3O2 Br 
 

 
v  k H 3O2 Br   kKH 2O2  H 3O  Br 
Geschwindigkeitsgesetz ~ experimental
f(Br-Konzentration, pH-Wert der Lösung)
Homogene Katalyse: Beispiele
Sauerkatalyse → Ubertragung eines Proton → Substrat:
X + HA → HX+ + AHX+
→ Produkte
Primar Prozess: - Solvolyse von Estern
- Keto-Enol-Tautomerie
Basenkatalyse → Ubertragung eines Proton (vom Substrat) → Base
XH + B → X- + HB
X→ Produkte
Erste Schritt: - Isomerisierung organischen Verbindungen
- Halogenierung ...
- Claisen- und Aldolkondensation
Enzymkatalysierte Reaktionen
Enzyme: homogene Biokatalysatoren → aktive Zentrum
Bindung → Substrate
Synthese → Produkte
- bleiben unverändern (nach Beendigung der Reaktion)
züruck
→ (meistens) proteine
→ (manche) aktiven Zentrum: enthalten anorganische/organische Cofaktoren
→ (bestimmte) RNA-Moleküle: bilden Rybosyme → katalitische Aktivität
Substrat: der Ausgangstoffe der Reaktion
Aufbau der aktiven Position → auf katalysierte Reaktion abgestimmt
Gruppen des Substrats + Gruppen des Enzyms
Wechselwirkungen (Wasserstoffbrücke, Elektrostatisch, van der Waals)
Molekülardurchmesen ≈ 10 – 100 nm → Makromolekülen
Enzymkatalysierte Reaktionen: Beispiele
NADH-quinone
oxidoreductase
Oxidoreduktasen = sie katalysieren Redoxreaktionen.
Transferasen = sie übertragen funktinelle Gruppen von einem Substrat auf
ein anderes.
RNA- Polymerase
Hydrolasen = sie spalten die Bindungen unter Einsatz von Wasser.
Isomerasen = sie
beschleunigen die die Umwandlung von chemischen
Isomeren.
Ligasen = sie katalysieren die Additionsreaktion mithilfe vn ATP.
Schlüssel-Schloss Prinzip
Dreidimensionalen Strukturen von
Schlüssel-Schloss Prinzip
Substrat ↔ activer Position → perfekt ineinander
passen → ohne wesentliche Verschibungen von
Atomen oder Bindungen
Experimentelle Untersuchungen → Induced-fit-Modell
Induced-fit-Modell
Die
Bindung
des
Substrat
↔
geeignete
Konformationsänderung des aktiven Zentrum
→ perfekt ineinander passen → passt das
Substrat optimal an die Bindungsstelle
Enzymkatalysierte Reaktionen
Störungsanfällig
Möleküle → gehemmt worden: Produktbildung verhindern
(spezifische Bindungen)
Therapieansätz → ständigen Verabreichung eines Inhibitors
↓
ein Enzym hemmt
↓
kann nicht eine Protein aufbauen
Beispiel: Immunschwächekrankenheit AIDS → die Hüllenprotein umgibt
das genetische Material
des Virus
das Virus kann sich nicht vermehren
Der Michaelis-Menten-Modell (1)
Die Reaktion Untersuchung → die Anfangsgeschwindigkeit der
Produktbildung in eine Lösung (sehr geringe Konzentrationen des Enzyms)
Die Reaktion → beschleunigt
[S] >> [Enzym]
([S] > 103 [Enzym] )
Grundlegende Merkmale - Produktbildung:
1. Die Anfangsgeschwindigkeit ~ [E]0 (Gesamtkonzentration des Enzyms)
– bei gegebenen [S]0 (Anfangskonzentration des Substrats)
2. Die Geschwindigkeit ~ [S]0 – bei gegebenen [E]0 + ↓ [S]0
3. Die Geschwindigkeit ≠ [S]0 – bei gegebenen [E]0 + ↑ [S]0 (Sättigung)
4. Die Geschwindigkeit – ein Maximal Vmax – bei gegebenen [E]0 + ↑ [S]0
1. Schritt → Michaelis-Menten Mechanismus – Zwischenverbindung
Enzym ↔ Substrat
2. Schritt → Enzym freigesetzt: Unverändert / nach einer Modifikation
Der Michaelis-Menten-Modell (2)
Reaktion:
ka
E+S
ES
t0 = 0 → [E]0 , [S]0
E+P
t
ka‘
kb
ES
→ [E]0 , [P]
Wichtig: kb‘ << kb → Rückreaktion – nicht berüchsichtigt
kb E 0
v
KM
1
[ S ]0
Michaelis-Menten Gleichung
k a'  kb
KM 
ka
Michaelis-Menten Konstante
Gleichgewicht:
1. v ~ [S]0 ← [S]0 << KM
2. v ≠ f([S]0) ← [S]0 >> KM
Begrundung der Michaelis-Menten-Modell (1)
v  kb
• die Gerschwindigkeit der Produktbildung
• die Konzentration des Enzym-Substrat Komplexes:
ES 
d ES 
 ka E S   ka' ES   kb ES 
dt
In dem pro Zeiteinheit → ebenso viele ES Komplexes: gebildet ≡ zerfallt
d[I ]
0
dt
Quasistationaritätprinzip:
• die Konzentration der Intermediate (per
Induktionsperioden)von null aus zunimmt
• im Verlauf der Reaktion → kaum ändert
ES   ' ka E S 
k a  kb
[E] → Konzentration des
freien Enzyms
[S] →Konzentration des
freien Substrats
Begrundung der Michaelis-Menten-Modell (2)
• die Michaelis-Menton Konstante
• Einheit für KM → molare Konzentration einheit
E 0  E   ES 
S   S 0
← [S] >> [E]
1
ES   E 0  ES S 
KM


1
ES 1  S   1 E 0 S 
 KM
 KM
ES K M  S   E 0 S 
k a'  kb E S 
KM 

ES 
ka
ES  
1
E S 
KM
ES   E 0 S 0
K M  S 0

E 0
KM
1
S 0
Begrundung der Michaelis-Menten-Modell (3)
Die Konzentration an Zwischenverbindungen
in quasistationären Zustand → f([S]0)
Die Geschwindigkeit der Produktbildung: v  k ES 
b
v
kb E 0
K
1 M
S 0
Michaelis-Menton Gleichung
Die Abhängigkeit der Geschwindigkeit einer
enzymkatalisierte Reaktion → f([S])
ES   EK0
1 M
S 0
Der Michaelis-Menten-Modell: Eigenschaften
[S]0 << [KM]
Die Reaktionsgeschwindigkeit ~ [S]0
KM
 1
S 0
ES   1 E 0 S 0  S 
KM
v
kb
E 0 S 0
KM
[S]0 >> [KM]
Die Geschwindigkeit erreicht einen
Maximal Wert VMax ≠ f([S]0)
KM
0
S 0
ES   E 0
v  kb E 0
Das Lineweaver-Burk Diagram
Die Geschwindigkeit einer
enzymkatalysierte Reaktion
1

v
 1 

f 
 S 0 
v
vMax
K
1 M
S 0
Linear Regression
↓
Lineweaver-Burk
Diagram
Die Auftragung 1  f  1  ist eine Gerade mit:
v
 S 0 
KM
•
→ die Steigerung der Gerade
vMax
1
•
→ der y-Achsenabschnitt
vMax
1

•
K M → der x-Achsenabschnitt
1
•
→ kb berechnen:
vMax
• ka und ka‘ → sind nicht zugänglich
1
1
K
1

 M
v vMax S 0 vMax
Enzymkatalysierte Reaktionen: Beispiele
1. Carboanhydrase
CO2 + H2O → HCO3- + H+
KM = 8 mM
kcat = 6*105 s-1
2. Superoxid dismutase:
O2- + 2H + → H2 O2 + O2
Aktuelle Anwendung (2008):
SOD im Nanoreaktoren:
Decay of Superoxide at pH 8, measured photometrically @ 280 nm
70
kcat / KM = 1*109 M-1 s-1
Blank
60
125 nM SOD
SOD+Dye in A10B100A10 Vessicles
50
40
relative Absorption
M(n+1)+-SOD + O2− → Mn+-SOD + O2
Mn+-SOD + O2− + 2H+ → M(n+1)+-SOD + H2O2.
30
20
10
0
-10
0
10
20
30
40
-10
Time [ms]
F. Axthelm, O. Casse, W. Koppenol, T. Nauser, W. Meier, C.G. Palivan, C.G; J.Chem.Phys.B, 2008, 112(28), 8211.
50
60
70
Die katalytische Effizienz
Die Wechselzahl (Katalysenkonstante) eines
Enzyms Kcat → Anzahl der Katalysenzyklen (an
K cat  K b 
einer aktiven Position) in einem bestimmten
Zeitinterval ablaufen / die Länge des Intervalls
Katalytische Effizienz ε → das Verhaltnis
↓
ε ↑ - effiziente Enzym

vmax
E 0
K cat
kk
 'b a
K M k a  kb
Wenn kb >> ka’ → ε ≈ ka’
ka → die Geschwindigkeitskonstante für die Bildung eines Komplexes
aus 2 Einheiten : ε ↔ maximalen Diffusionsgeschwindigkeit von E und S
(in der Lösung)
ε = 4∙108 dm3mol-1s-1 Catalase
↓
die Geschwindigkeit der Reaktion → durch die Diffusion bestimmt
z.Beispiel :
Die katalytische Effizienz von Carboanhydrase
Carboanhydrase: [E0] = 2.3x10-9 mol dm-1
CO2 + H2O → HCO3- + H+
Lineweaver-Burk Diagramm:
vmax = 0.250 mmol dm-3 s-1
KM = Steigung/(y Achsenabschnitt) = 10 mmol dm-3
kcat = vmax / [E0] = 1.1 x105 s-1
ε = 1.1 x∙107 dm3mol-1s-1
Mechanismen der Enzymhemmung (1)
Enzymhemmung:
ein
Inhibitor
setzt
die
Geschwindigkeit
der
Produktbildung am Substrat herab, indem er selbst an das Enzym, den
Enzym-Substrat-Komplex oder beide gleichzeitig bindet.
Allgemeine kinetische Schema für die Hemmung:
Reaktion:
ka
E+S
ES
t0 = 0 → [E]0 , [S]0
ka‘
ES
EI
ESI
kb
KI
KI‘
E+P
E+I
ES + I
E I 
KI 
EI 
KI &
KI
'

ES I 

ESI 
KI‘
Effiziente
Inhibitoren
Mechanismen der Enzymhemmung (2)
Die Geschwindigkeit der Produktbildung:
v  kb ES 
Die Reaktionsgeschwindigkeit in Anwesenheit eines
Inhibitors:
mit:

I
  1
KI

I
 '  1
v
vmax
KM
 '
S 0
K I'
Die Ausdruck kann mithilfe eines Lineweaver-Bruck-Diagramms
ausgewartet werden:
1  ' K M 1


v vmax vmax S 0
Mechanismen der Enzymhemmung (3)
a) Kompetitive Hemmung = I bindet lediglich an
die aktive Position des Enzyms:
 > 1 und ’ = 1
b) Unkompetitiven Hemmung = der Inhibitor
bindet an das Emzym, aber nicht an dessen
aktive Position:
 = 1 und ’ > 1
c) Nicht kompetitive Hemmung = der Inhibitor
bindet an einer anderen als der aktiven Position
und seine Anwesenheit das S daran hindert:
 > 1 und ’ > 1
Substrat
Enzym
nicht-kompetitiver
Inhibitor
Die Kinetik zusammengesetzter Reaktionen:
Lernziele
 Beispiele von zusammengesetzter Reaktionen
 Homogene Catalyse: Merkmale homogen-catalysierter Reaktionen
 Enzymcatalysierte Reaktionen
 P. Atkins, J. de Paula, “Physikalische Chemie”, Wiley-VCH Verlag GmbH&
Co, 2006, 23.3.
 G. Wedler, H-J. Freund, „Lehrbuch der Physikalischen Chemie“, Wiley-VCH
Verlag GmbH& Co, 2010, 6.7.2
Prüfung
Vorbemerkungen:
 Von den 6 Aufgaben sind 6 zu lösen.
Tragen Sie Ihre Endergebnisse in die vorgesehenen Felder ein. Achten
Sie auf die Einheiten!
 Lösungen ohne Herleitung oder Begründung sind ungültig. Geben Sie
die verwendeten Formeln an und schreiben Sie Ihre Rechenschritte auf.
 Eine A4 Handschriftseite mit Formeln