Satz von Gauss, Fluss und Divergenz

Satz von Gauss, Fluss und Divergenz
y
3
−→
F
2
1
-3
-2
-1
1
2
3
4
x
-1
-2
L
−→
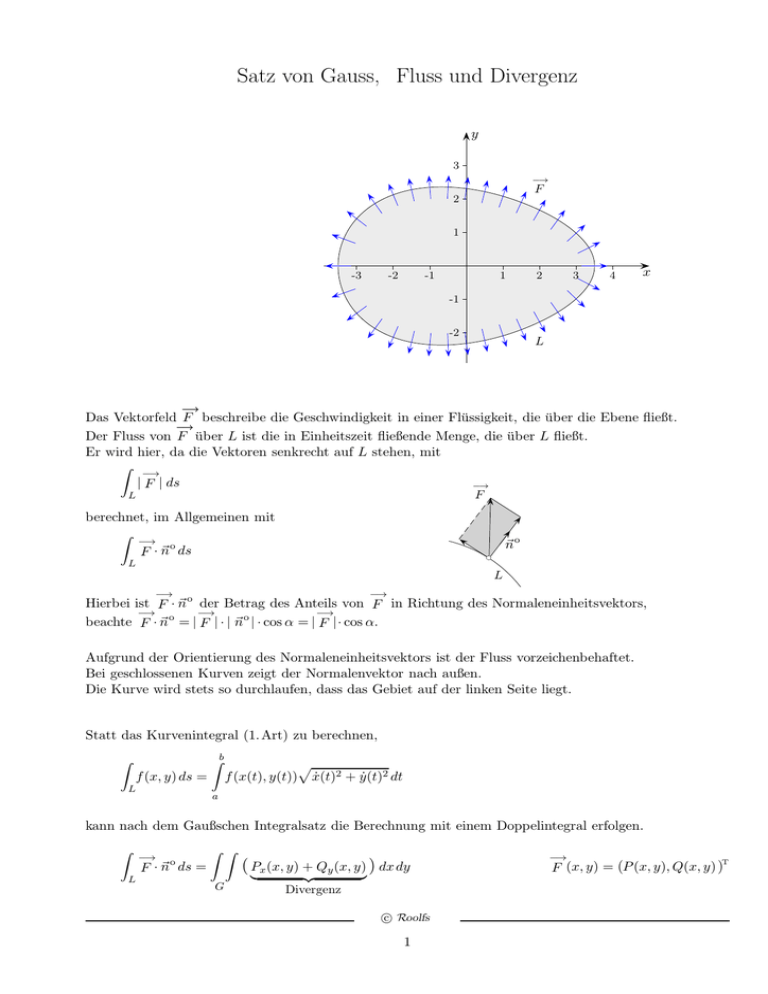
Das Vektorfeld F beschreibe die Geschwindigkeit in einer Flüssigkeit, die über die Ebene fließt.
−→
Der Fluss von F über L ist die in Einheitszeit fließende Menge, die über L fließt.
Er wird hier, da die Vektoren senkrecht auf L stehen, mit
Z
−→
| F | ds
−→
F
L
berechnet, im Allgemeinen mit
Z
−→ o
F · ~n ds
bc
~n o
L
L
−→
−→
Hierbei ist F · ~n o der Betrag des Anteils von F in Richtung des Normaleneinheitsvektors,
−→
−→
−→
beachte F · ~n o = | F | · | ~n o | · cos α = | F |· cos α.
Aufgrund der Orientierung des Normaleneinheitsvektors ist der Fluss vorzeichenbehaftet.
Bei geschlossenen Kurven zeigt der Normalenvektor nach außen.
Die Kurve wird stets so durchlaufen, dass das Gebiet auf der linken Seite liegt.
Statt das Kurvenintegral (1. Art) zu berechnen,
Z
f (x, y) ds =
L
Zb
a
p
f (x(t), y(t)) ẋ(t)2 + ẏ(t)2 dt
kann nach dem Gaußschen Integralsatz die Berechnung mit einem Doppelintegral erfolgen.
Z
L
−→
o
F · ~n ds =
Z Z
G
( Px (x, y) + Qy (x, y) ) dx dy
|
{z
Divergenz
}
c Roolfs
1
−→
T
F (x, y) = (P (x, y), Q(x, y) )
Satz von Gauss in der Ebene
Z
−→
o
F · ~n ds =
L
ZZ
−→
(Px (x, y) + Qy (x, y)) dx dy
T
F (x, y) = (P (x, y), Q(x, y) )
G
−→
Gegeben ist das Vektorfeld F = (x, y )T und die Kreisfläche A mit dem Radius 2.
y
2
1
-2
-1
1
2
x
-1
-2
Die Länge der Vektoren wurde halbiert.
p
x
x
1
·p
= x2 + y 2
F · ~n =
y
x2 + y 2 y
−→
o
−→
Längs des Kreises K: x2 + y 2 = 4 besitzt die Normalkomponente von F den konstanten Wert 2.
Das Kurvenintegral hat daher den Wert:
Z
Z
−→ o
·
~
n
ds
=
2
ds = 8π
F
K
K
Andererseits gilt:
ZZ
ZZ
(Px (x, y) + Qy (x, y)) dx dy =
2 dA = 2 · 4π = 8π
A
A
c Roolfs
2
Fluss durch eine Würfeloberfläche
z
y
x
−→
T
Gegeben ist das Vektorfeld
F = (4xz, −y 2 , yz ) .
ZZ
−→ o
Es soll der Fluss
F · ~n dA durch die Oberfläche A des Würfels mit der Kantenlänge 1
berechnet werden.
Die Oberfläche des Würfels besteht aus 6 Quadratflächen.
 
ZZ
ZZ
0
−→ o
A1 : ~n o =  1 , y = 1,
F · ~n dA1 =
0
!
4xz
−1
z
 
ZZ
ZZ
0
−→ o
o


A2 : ~n = 0 , z = 1,
F · ~n dA2 =
1
!
4x
−y 2
y
 
ZZ
ZZ
1
−→ o
o


A3 : ~n = 0 , x = 1,
F · ~n dA3 =
0
·
0
1
0
·
0
0
1
!
4z
−y 2 ·
yz
1
0
0
!
!
!
dA1 =
ZZ
−1 dA1 = −1
dA2 =
ZZ
Z1 Z1
dA3 =
ZZ
−→
1
o
F · ~n dA = −1 + 2 + 2 + 0 + 0 + 0 = 1,5
alternativ mit dem Satz von Gauss:
ZZ
ZZZ
Z1Z1Z1
−→ o
−→
div F dV =
(4z − y) dxdydz = . . . = 1,5
F · ~n dA =
0 0 0
c Roolfs
3
1
y dxdy = . . . = 2
0 0
4z dA3 = 4
...
ZZ
y dA2 =
Z1 Z1
0 0
z dydz = . . . = 2
Satz von Gauss im Raum
ZZ
−→
o
F · ~n dA =
A
ZZZ
V
( Px (x, y) + Qy (x, y) + Qy (x, y) ) dx dy dz
|
{z
−→
Divergenz div ( F )
}
−→
T
F (x, y) = (P (x, y), Q(x, y), R(x, y) )
−→
Gegeben ist das Vektorfeld F = (x3 , −y, z )T .
Es soll der Fluss durch die Oberfläche A eines Zylinders mit R = 2 und H = 5 berechnet werden.
z
y
x
ZZZ
−→
div ( F ) dxdy dz =
V
ZZZ
2
3x dxdy dz
Zylinderkoordinaten
=
V
ZZZ
f (r · cos ϕ, r · sin ϕ, z) r dz dr dϕ
V
Z2πZ2 Z5
= 3·
(r · cos ϕ)2 r dz dr dϕ
0 0 0
Z2π
Z2 Z5
2
= 3 · cos ϕ
r 3 dz dr dϕ
0
0 0
= ...
Z2π
cos 2ϕ + 1
dϕ
= 60 ·
beachte cos 2ϕ = 2 cos2 ϕ − 1
2
0
= 60π
c Roolfs
4
Ohne den Satz von Gauss
−→
Gegeben ist das Vektorfeld F = (x3 , −y, z )T .
ZZ
−→ o
Es soll der Fluss
F · ~n dA durch die Oberfläche A eines Zylinders mit R = 2 und H = 5
direkt berechnet werden.
z
y
x
Die Oberfläche des Zylinders teilt sich auf in Deckel, Boden und Mantel.
 
0
Deckel: z = 5, ~n o =  0,
1
ZZ


0
Boden: z = 0, ~n o =  0,
−1
ZZ
−→
o
F · ~n dD =
−→
o
ZZ
F · ~n dB =
5 dD = 20π
ZZ
0 dB = 0
Mantel in Zylinderkoordinaten:
~r =
o
~n =
!
2 cos ϕ
2 sin ϕ , ϕ ∈ [0; 2π], z ∈ [0; 5]
z
!
cos ϕ
sin ϕ ,
0
ZZ
−→
o
F · ~n dM =
ZZ
!
8 cos3 ϕ
−2 sin ϕ
z
·
!
ZZ
cos ϕ
sin ϕ dM =
(8 cos4 ϕ − 2 sin2 ϕ)dM
0
Z2πZ5
=
(8 cos4 ϕ − 2 sin2 ϕ) · 2 dz dϕ = 40π
0 0
ZZ
−→
o
F · ~n dA = 60π
beachte |
c Roolfs
5
∂~r
∂~r
×
| = | (2 cos ϕ, 2 sin ϕ, 0 )T | = 2
∂ϕ
∂z
Oberflächenintegral
z
v
3
2
1
D
1
1
2
3
2
3
x
u
Sei ~r = (x(u, v), y(u, v), z(u, v) )T eine Parameterdarstellung der Fläche S.
Für eine Funktion f (x, y, z) lautet das Flächenintegral:
ZZ
∂~r
∂~r
×
| dudv
f (x(u, v), y(u, v), z(u, v) ) · |
∂u
∂v
D
−→
Der Fluss eines Vektorfeldes F durch die Fläche ist
ZZ
S
−→
o
F · ~n dS =
ZZ
−→
F·
D
∂~r
∂~r
×
∂u
∂v · | ∂~r
∂~r
∂u
∂~r
|
×
|
∂v
∂u
±
∂~r
×
| dudv =
∂v
Das Vorzeichen des Vektorprodukts ist so zu wählen,
dass der Normalenvektor nach außen zeigt.
c Roolfs
6
ZZ
D
−→
F ·[ ±
∂~r
∂~r
×
] dudv
∂u
∂v
y
Satz von Gauss im Raum
ZZ
−→
o
F · ~n dA =
A
ZZZ
V
( Px (x, y) + Qy (x, y) + Qy (x, y) ) dx dy dz
|
{z
}
−→
Divergenz div ( F )
−→
T
F (x, y) = (P (x, y), Q(x, y), R(x, y) )
−→
Gegeben ist das Vektorfeld F = (z, y, z + 1 )T .
Es soll der Fluss durch die Oberfläche A eines Kegels mit R = 2 und H = 6 berechnet werden.
z
6
5
4
3
2
1
1
2
3
x
ZZZ
−→
div ( F ) dxdy dz =
V
ZZZ
2 dxdy dz
Kegel
=
2 · 8π = 16π
V
c Roolfs
7
1
2
3
y
Ohne den Satz von Gauss
−→
Gegeben ist das Vektorfeld F = (z, y, z + 1 )T .
ZZ
−→ o
Es soll der Fluss
F · ~n dA durch die Oberfläche A eines Kegels mit R = 2 und H = 6
direkt berechnet werden.
z
6
5
4
3
2
1
1
1
2
3
2
y
3
x
Die Oberfläche des Kegels teilt sich auf in Boden und Mantel.


0
Boden: z = 0, ~n o =  0,
−1
ZZ
−→
o
F · ~n dB =
ZZ
−1 dB = −4π
Mantel in Zylinderkoordinaten:
!
~r =
2r cos ϕ
2r sin ϕ , ϕ ∈ [0; 2π], r ∈ [0; 1]
6(1 − r)
∂~r
∂~r
×
=
∂ϕ
∂r
ZZ
ZZ
ZZ
o
F · ~n dM = 4r
−→
M
!
−2r sin ϕ
2r cos ϕ ×
0
!
2 cos ϕ
2 sin ϕ
−6
!
!
3 cos ϕ
= −4r 3 sin ϕ
1
6(1 − r)
2r sin ϕ ·
7 − 6r
!
ZZ
3 cos ϕ
3 sin ϕ dM = 4r
(18 cos ϕ − 18r cos ϕ − 6r cos2 ϕ + 7)dM
1
2π 1
Z Z
= 4r
(
0 0
−→
o
F · ~n dA = 16π
A
c Roolfs
8
···
) dr dϕ = 20π
Anschauung
y
−→
F
x
−→
Nehmen wir an, das Vektorfeld F beschreibt die Strömung einer Flüssigkeit in einem Volumen V
−→
mit durchlässiger Oberfläche. Die Divergenz von F erfasst die Stärke von allen Quellen und Senken
in einzelnen Punkten.
Um zu erfassen, wie viel Flüssigkeit aus V herausfließt, kann ermittelt werden, wie viel Flüssigkeit
durch die Oberfläche von V aus- und eintritt. Dies entspricht dem Durchfluss von senkrechten
Komponenten auf der Oberfläche (Oberflächenintegral).
Alternativ kann nach dem Satz von Gauss für das Innere von V untersucht werden, wie viel Flüssigkeit in Senken versickert und aus Quellen sprudelt (Volumenintegral über die Divergenz).
c Roolfs
9
Fluss und Divergenz
−→
Das Vektorfeld F beschreibe wieder die Geschwindigkeit
in einer Flüssigkeit, die über die Ebene fließt.
−→
Der Fluss von F über L ist die in Einheitszeit fließende Menge,
die über L (häufig geschlossen) fließt, er wird mit
Z
−→ o
F · ~n ds
bc
L
−→
bc
berechnet.
Aufgrund der Orientierung des Normaleneinheitsvektors
ist der Fluss vorzeichenbehaftet. Bei geschlossenen Kurven
zeigt der Normalenvektor nach außen. Die Kurve wird stets
so durchlaufen, dass das Gebiet auf der linken Seite liegt.
F
~n o
L
Nach dem Gaußschen Integralsatz kann die Berechnung mit einem Doppelintegral erfolgen.
Z Z
Z
−→ o
·
~
n
ds
=
( Px (x, y) + Qy (x, y) ) dx dy
F
|
{z
}
L
G
Divergenz
Q(C)
y
~n3o
y
P
F = Q
−→
C
bc
D
~n4o
bc
bc
M
B
bc
~n2o
P (B)
bc
L
A
~n1o
x
x
Wir untersuchen den Fluss für ein kleines Quadrat (ds = a):
Z
−→
o
F · ~n ds =
L
P (A)
!
Q(A)
· ~n1o
+
!
P (B)
Q(B)
· ~n2o
+
!
P (C)
Q(C)
· ~n3o
= −Q(A)a + P (B)a + Q(C)a − P (D)a
=
( P (B) − P (D)) a
=
( Px (M ) + Qy (M )) a2
+
+
!
P (D)
Q(D)
· ~n4o
beachte |P (D)| = −P (D)
( Q(C) − Q(A)) a
−→
= div F a2
Die Divergenz gibt den lokalen Fluss pro Einheitsfläche an, der von M wegfließt (divergiert).
c Roolfs
10
Singularität im Ursprung
y
4
3
2
1
-4
-3
-2
-1
1
2
3
4
x
-1
-2
-3
-4
Das Vektorfeld einer typischen ebenen Quelle hat die Form (nicht im Ursprung definiert)
!
!
x
x
1
1
1
p
= 2
~v (x, y) = p
.
x + y2 y
x2 + y 2
x2 + y 2 y
| {z } |
{z
}
1/r
Länge 1
Potential (leicht zu verifizieren)
1
V (x, y) = 2 ln(x2 + y 2 )
Fluss für einen Kreis um den Ursprung mit dem Radius r
1
~v · ~n o = p
x2 + y 2
| {z }
1/r
beachte: ~n o · ~n o = 1
Das Kurvenintegral hat daher den Wert
Z
1
~v · ~n o ds = r 2πr = 2π
und ist unabhängig von r.
K
Mit größer werdendem Radius wird der Fluss/Längeneinheit schwächer,
der Umfang wächst jedoch.
c Roolfs
11
Singularität im Ursprung
y
4
3
2
1
-4
-3
-2
-1
1
2
3
4
x
-1
-2
-3
-4
Die Divergenz für einen Bereich, der den Ursprung nicht enthält, beträgt null.
!
x
1
~v (x, y) = 2
.
x + y2 y
div ~v (x, y) =
y 2 − x2
x2 − y 2
+
=0
(x2 + y 2 )2
(x2 + y 2 )2
Nach dem Satz von Gauss ist der Fluss für solche Bereiche dann null.
In unserem Fall kann dies direkt eingesehen werden, da der Fluss der Kreisabschnitte jeweils
der gleiche Anteil von 2π ist, für eine Randkurve jedoch mit unterschiedlichem Vorzeichen.
Diese Überlegungen können auf den R3 erweitert werden.
An die Stelle des Faktors 1/r tritt 1/r 2 .


x
x
1
1
1
y =
y
p
~v (x, y, z) = 2
3/2
2
2
2
x + y2 + z 2
(x2 + y 2 + z 2 )
|
{z
} x +y +z
z
z
|
{z
}
1/r 2
Länge 1
Der Fluss für eine Kugel um den Ursprung beträgt dann 4π (gleiche einfache Überlegung).
c Roolfs
12
Elektrische und magnetische Felder
y
4
3
2
1
-4
-3
-2
-1
1
2
3
4
x
-1
-2
-3
-4
Die Grafik veranschaulicht, dass der Fluss für einen beliebigen Rand im R2
oder R3 jeweils 2π bzw. 4π beträgt, sofern der Ursprung (die Quelle) umschlossen wird.
Daraus folgern wir, dass der Fluss mehrerer radialsymmetrischer Felder, die mit dem Faktor 1/r 2
abklingen und sich additiv überlagern (wir bleiben im R3 ), nur von der Anzahl der Quellen innerhalb
der umschließenden Oberfläche abhängt und nicht von deren Form.
Für ein elektrisches Feld erscheint es nun naheliegend, dass der Fluss durch eine geschlossene
Oberfläche S eines Volumens V direkt proportional zur elektrischen Ladung Q in seinem Inneren
ist (Maxwell). Z Z
X
−→ o
−→ X
E · ~n dS = 4πQ
E =
qi~v (x − xi , y − yi , z − zi ), Q =
qi
S
Magnetfelder sind quellenfrei, ihre Feldlinien stets geschlossen.
Der magnetische Fluss durch eine geschlossene Oberfläche eines Volumens ist null (Maxwell).
ZZ
−→ o
B · ~n dS = 0
S
c Roolfs
13
Magnetische Induktion
−→
∂B
∂t
−→
E
◦
◦
−→
−→
Ein sich zeitlich veränderndes Magnetfeld B erzeugt ein elektrisches Feld E.
Dies führt z. B. an einer Drahtschleife C zu einer Induktionspannung.
Es gelten die Beziehungen:
−→
∂
−→
−→
B
rot E = − ∂t
Uind =
Φ=
Z
B (x, y, z, t)
−→
E d~s
Wegintegral
C
ZZ
−→
B · ~n o dA
magnetischer Fluss, Oberflächenintegral, A Fläche der Leiterschleife
A
∂Φ
Uind = − ∂t
c Roolfs
14
Elektrische Induktion
−→
B
−→
∂E
∂t
−→
B
Ist eine Leiterschleife durch einen Kondensator
unterbrochen und fließt ein Strom, dann lädt sich
−→
der Kondensator auf. Das elektrische Feld E im Kondensator wächst linear mit der Zeit an.−→
Um dieses sich zeitlich ändernde elektrisches Feld herum wird ein magnetisches Wirbelfeld B erzeugt.
Die Maxwell-Gleichungen sind nicht völlig symmetrisch aufgebaut, denn während ein elektrisches
Wirbelfeld ausschließlich durch die zeitliche Änderung des magnetischen Flusses entsteht (Faraday),
kann ein magnetisches Wirbelfeld zwei Ursachen haben: den üblichen Leitungsstrom (Oersted) oder
die zeitliche Änderung des elektrischen Flusses (Maxwell).
Es gilt die Beziehung:
−→
∂E
rot B = µ0~j + µ0 ǫ0 ∂t
−→
~j Stromdichte, Richtung des Stromflusses,
Einheit: Stromstärke/Leiterquerschnitt
µ0 , ǫ0 physikalische Konstanten
Mit der Integralform wird eine andere Blickrichtung eingenommen.
Für eine in den Raum gelegte Fläche S bilden wir das Flächenintegral.
ZZ
ZZ
Z Z −→
−→
∂E
~j · ~n o dS + µ0 ǫ0
rot B · ~n o dS = µ0
n o dS
∂t · ~
S
S
I
−→
S
d
ZZ
B d~x = µ0 IS + µ0 ǫ0 dt
∂S
−→
E · ~n o dS
S
Die linke Seite wurde mit Hilfe des Stokesschen Integralsatzes in ein Wegintegral (magnetische Zirkulation)
über die Randkurve ∂S umgewandelt. Der erste Summand auf der rechten Seite ist gleich µ0 mal dem durch
die Fläche S fließenden elektrischen Strom. Im zweiten Summanden ziehen wir die partielle Zeitableitung
(die dadurch zu einer einfachen Zeitableitung wird) heraus.
c Roolfs
15
Punktladung
Die Punktladung q erzeugt das elektrische Feld
 
x
−→
q
y = q ~x.
E=
3/2
| ~x | 3
(x2 + y 2 + z 2 )
z
Für jede umschließende Oberfläche S gilt
ZZ
−→ o
E · ~n dS = 4πq.
S
Nach dem Satz von Gauss
ZZ
ZZZ
−→ o
−→
E · ~n dS =
div E dV
S
V
−→
ist mit div E = 0 die rechte Seite jedoch null.
Bei näherem Hinsehen erkennen wir, dass der Satz von Gauss nicht anwendbar ist.
−→
E und div E sind im Ursprung nicht definiert.
−→
Die physikalische Vorstellung des Satzes wäre bestechend. Der Fluss durch die Oberfläche wäre
proportional zur umschlossenen Ladung, die hier im Ursprung konzentriert ist und als Quelle wirken
−→
würde. Außerhalb des Ursprungs liegen mit div E = 0 keine Quellen vor.
Physiker wissen sich zu helfen. Sie führen ein Objekt δ3 ein mit den Eigenschaften
ZZZ
q4πδ3 (~x) dV = 4πq,
δ3 (~x) = 0 für ~x 6= ~0,
δ3 (~0) = ∞
V
und nennen es (dreidimensionale) Delta-Funktion
(obwohl es keine Funktion ist, δ3 = δ(x)δ(y)δ(z), siehe Diracsche Delta-Funktion).
c Roolfs
16
Elektromagnetische Wellen
Ein sich zeitlich änderndes magnetisches Feld ist seinerseits von einem sich zeitlich ändernden elektrischen
Wirbelfeld umschlossen. Dieses wiederum wird von einem sich zeitlich ändernden Magnetfeld umschlossen,
das von einem elektrischen Wirbelfeld umschlossen wird, usw.
Dies führte Maxwell 1868 zu der Voraussage:
Ein sich zeitlich änderndes elektromagnetisches Feld breitet sich im Raum
als elektromagnetische Welle aus.
−→
E (t)
−→
B (t)
c Roolfs
17
Wellengleichung
Betrachtet man die Maxwellschen Gleichungen im Vakuum, also im quellenfreien Raum
und vernachlässigt somit Ladungen und Ströme, so lassen sich die Gleichungen wie folgt schreiben:
−→
a)
∇· E = 0
b)
∇· B = 0
c)
∇× E = − ∂t B
d)
∇× B = −µ0 ǫ0 ∂t E
−→
∂
−→
−→
∂
−→
−→
Nochmaliges Anwenden der Rotation auf c) ergibt
∂
−→
e)
−→
∇ ×(∇× E ) = ∇ ×(− ∂t B )
Für beliebige Vektorfelder gilt:
−→
−→
−→
∇ ×(∇× H ) = ∇(∇· H ) − ∇2 H
∇2 = ∇ · ∇
Damit erhalten wir aus e) unter Berücksichtigung von a):
f)
∂
−→
∂
−→
−→
∇ ×(− ∂t B ) = − ∂t (∇× B ) = −∇2 E
und mit d) folgt
µ 0 ǫ0
−→
∂ 2 −→
E = ∇2 E
2
∂t
Beschränkt man sich auf Änderungen in einer Dimension, so kann man den Laplace-Operator ∇2 (= ∆)
durch
∂2
ersetzen und erhält damit die Wellengleichung einer ebenen elektromagnetischen Welle.
∂x2
∂ 2 −→
∂ 2 −→
E
=
µ
ǫ
E
0
0
∂x2
∂t2
Wendet man die Rotation auf d) an, erhält man analog
∂ 2 −→
∂ 2 −→
B
=
µ
ǫ
B
0
0
∂x2
∂t2
c Roolfs
18
Elektromagnetische Wellen
Elektromagnetische Wellen wurden 1886 von H. Hertz erstmals mit Hilfe von
elektrischen Schwingkreisen erzeugt.
−→
E (t)
−→
B (t)
Eine mögliche Lösung für
∂ 2 −→
∂ 2 −→
E = µ 0 ǫ0 2 E
2
∂x
∂t
lautet
−→
E (x, t) = Emax sin(ωt − kx)
∂ 2 −→
E (x, t) = −Emax sin(ωt − kx)k2
∂x2
∂ 2 −→
E (x, t) = −Emax sin(ωt − kx)ω 2
∂t2
mit
k2
= µ 0 ǫ0 .
ω2
c Roolfs
19
Partielle Integration
Aus der Produktregel
−→
−→
−→
div(g ·F ) = g · div F + grad g · F
folgt wie im Eindimensionalen die Regel für die partielle Integration,
die mit dem Satz von Gauss umgeschrieben werden kann.
Z
A
−→
g · div F dA =
Z
−→
div(g ·F ) dA −
| AZ
{z
}
Z
−→
grad g · F dA
A
−→
o
F · ~n ds
∂A
c Roolfs
20