17.3 Normalverteilte Zufallsgrößen

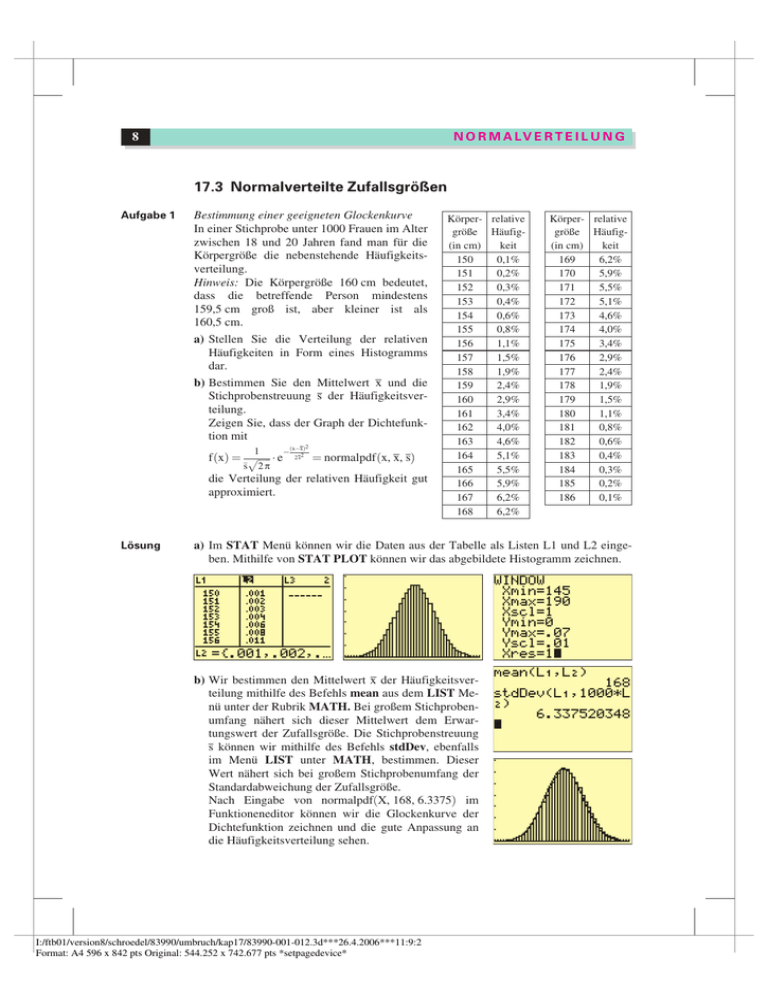
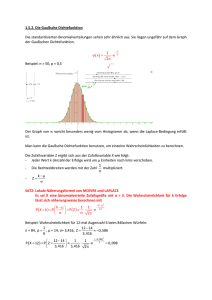
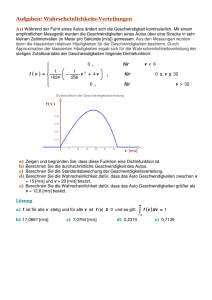
8
N O R M A LV E R T E I L U N G
17.3 Normalverteilte Zufallsgrßen
Aufgabe 1
Bestimmung einer geeigneten Glockenkurve
In einer Stichprobe unter 1000 Frauen im Alter
zwischen 18 und 20 Jahren fand man fr die
Krpergrße die nebenstehende Hufigkeitsverteilung.
Hinweis: Die Krpergrße 160 cm bedeutet,
dass die betreffende Person mindestens
159,5 cm groß ist, aber kleiner ist als
160,5 cm.
a) Stellen Sie die Verteilung der relativen
Hufigkeiten in Form eines Histogramms
dar.
b) Bestimmen Sie den Mittelwert x und die
Stichprobenstreuung s der Hufigkeitsverteilung.
Zeigen Sie, dass der Graph der Dichtefunktion mit
1
fðxÞ ¼ pffiffiffiffiffiffi e
s 2 p
ðxxÞ2
2 s2
¼ normalpdfðx, x, s)
die Verteilung der relativen Hufigkeit gut
approximiert.
Lsung
Krper- relative
grße Hufigkeit
(in cm)
150
0,1%
151
0,2%
152
0,3%
153
0,4%
154
0,6%
155
0,8%
156
1,1%
157
1,5%
158
1,9%
159
2,4%
160
2,9%
161
3,4%
162
4,0%
163
4,6%
164
5,1%
165
5,5%
166
5,9%
167
6,2%
168
6,2%
Krper- relative
grße Hufigkeit
(in cm)
169
6,2%
170
5,9%
171
5,5%
172
5,1%
173
4,6%
174
4,0%
175
3,4%
176
2,9%
177
2,4%
178
1,9%
179
1,5%
180
1,1%
181
0,8%
182
0,6%
183
0,4%
184
0,3%
185
0,2%
186
0,1%
a) Im STAT Men knnen wir die Daten aus der Tabelle als Listen L1 und L2 eingeben. Mithilfe von STAT PLOT knnen wir das abgebildete Histogramm zeichnen.
b) Wir bestimmen den Mittelwert x der Hufigkeitsverteilung mithilfe des Befehls mean aus dem LIST Men unter der Rubrik MATH. Bei großem Stichprobenumfang nhert sich dieser Mittelwert dem Erwartungswert der Zufallsgrße. Die Stichprobenstreuung
s knnen wir mithilfe des Befehls stdDev, ebenfalls
im Men LIST unter MATH, bestimmen. Dieser
Wert nhert sich bei großem Stichprobenumfang der
Standardabweichung der Zufallsgrße.
Nach Eingabe von normalpdf(X, 168, 6.3375) im
Funktioneneditor knnen wir die Glockenkurve der
Dichtefunktion zeichnen und die gute Anpassung an
die Hufigkeitsverteilung sehen.
I:/ftb01/version8/schroedel/83990/umbruch/kap17/83990-001-012.3d***26.4.2006***11:9:2
Format: A4 596 x 842 pts Original: 544.252 x 742.677 pts *setpagedevice*
Normalverteilte Zufallsgrßen
9
Information Normalverteilte Zufallsgrßen
Die Hufigkeitsverteilung fr die Krpergrße von Frauen zwischen 18 und 20 Jahren
in Aufgabe 1 konnten wir gut durch eine Dichtefunktion vom Typ
1
ðxmÞ2
2 s2
fðxÞ ¼ pffiffiffiffiffiffi e
s
2p
¼ normalpdf (x, m, s) approximieren.
In Medizin, Naturwissenschaften, Technik und anderen Wissenschaften treten oft Verteilungen von Zufallsgrßen auf, die durch den Graphen einer solchen Dichtefunktion
beschrieben werden. Zufallsgrßen, die eine stetige Dichtefunktion dieses Typs haben,
bezeichnet man als normalverteilt, daher auch die Bezeichnung normalpdf im GTR.
Aufgabe 2
Wahrscheinlichkeitsbestimmungen bei gegebenen normalverteilten Zufallsgrßen
In bestimmten Altersstufen kann die Krpergrße von Kindern als normalverteilt angesehen werden. Aus dem Diagramm kann man beispielsweise ablesen, dass jeweils 3%
der Vierjhrigen kleiner als 96 cm und grßer als 111 cm sind.
Bei den Vorsorgeuntersuchungen von Kindern wird geprft, ob die Krpergrße des untersuchten Kindes auffllig groß oder klein ist, d. h. ob es zu den 3% am oberen oder am
unteren Ende der Verteilung gehrt.
Hinweis: Beachten Sie, dass mit der Krpergrße 96 cm das Intervall [95,5 cm;
96,5 cm[ gemeint ist.
a) Bestimmen Sie aus diesen Angaben die bentigten Parameterwerte und s.
b) Wieviel Prozent der Vierjhrigen sind
(1) grßer als 99 cm,
(2) zwischen 99 cm und 102 cm groß?
Lsung
a) Wegen der Symmetrie der Normalverteilung liegt in der Mitte zwischen 95,5 cm
und 111,5 cm, also: = 103,5 cm.
Um die Standardabweichung s zu bestimmen, betrachten wir die Funktion
s(x) = normalcdf (95.5, 111.5, 103.5, x), die uns zu verschiedenen Werten fr die
Standardabweichung s Wahrscheinlichkeiten fr das Intervall [95,5 cm; 96,5 cm[
liefert.
Gesucht ist also diejenige Zahl x, fr die s(x) = 0,94
ist. Eine solche Zahl finden wir mithilfe der Wertetabelle der Funktion.
I:/ftb01/version8/schroedel/83990/umbruch/kap17/83990-001-012.3d***27.4.2006***10:52:52
Format: A4 596 x 842 pts Original: 544.252 x 742.677 pts *setpagedevice*
10
N O R M A LV E R T E I L U N G
Eine andere Mglichkeit: Wir betrachten die Gerade mit y = 0,94 parallel zu x-Achse und bestimmen mithilfe des Befehls intersect aus dem CALC-Men den Schnittpunkt beider Graphen. Die erste Koordinate liefert ebenfalls den gesuchten Wert
s » 4,25.
b) (1) P(grßer als 99 cm) = 1 – P(hchstens 99,5 cm groß)
= 1 – normalcdf (0, 99.5, 103.5, 4.25) = 0,8267
(2) P(zwischen 99 cm und 102 cm)
= P(mindestens 99,5 cm und hchstens 101,5 cm groß)
= normalcdf (99.5, 101.5, 103.5, 4.25) = 0,1457
bungsaufgaben
3.
Berechnen Sie mit den Ergebnissen = 103,5 und s = 4,25 aus Aufgabe 2 die folgenden Wahrscheinlichkeiten: Wieviel Prozent der 4-Jhrigen sind
a) kleiner als 103,5 cm,
b) zwischen 98,5 cm und 105,5 cm,
c) hchstens 104,5 cm groß?
4.
a) Bestimmen Sie mithilfe der Grafik den Erwartungswert und die Standardabweichung
der Krpergrße von Kindern im Alter
(1) von 6 Monaten;
(2) von 12 Monaten.
b) Bestimmen Sie und s fr die Krpergrße von Kindern mit dem Krpergewicht
(1) 6 kg;
(2) 8 kg.
I:/ftb01/version8/schroedel/83990/umbruch/kap17/83990-001-012.3d***27.4.2006***11:11:39
Format: A4 596 x 842 pts Original: 544.252 x 742.677 pts *setpagedevice*