11 Seiten

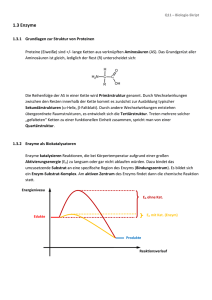
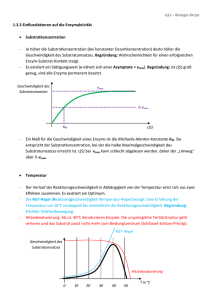
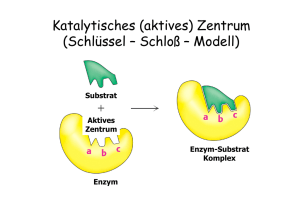
34
3.
Probe in den Lichtweg bringen und E ablesen.
Wird die Wellenlänge verändert, so muss das Photometer wieder neu geeicht werden, weil die
Intensität der Lichtquelle und die Empfindlichkeit der Photozelle mit der Wellenlänge ändert.
ENZYMREAKTIONEN
An fast allen chemischen Umsetzungen im Organismus sind Enzyme beteiligt. Enzyme sind
Katalysatoren, welche die Stoffwechselprozesse unter den milden Bedingungen in der Zelle (niedrige
Metabolitkonzentrationen, niedrige Temperatur, neutraler pH-Wert) ermöglichen.
Die wesentliche Eigenschaft eines Enzyms ist sein Vermögen, eine spezifische Reaktion ganz enorm
zu beschleunigen (= katalysieren). Dabei werden die Geschwindigkeiten der Vorwärts- und der
Rückwärts-Reaktion proportional erhöht, d.h. das chemische Gleichgewicht der Reaktion wird
nicht verändert. Die im Reaktionsablauf verbrauchte Verbindung bezeichnet man als Substrat, die
neugebildete als Produkt. Bei der Rückwärtsreaktion sind die Begriffe vertauscht (z.B. Acetaldehyd
und Aethylalkohol sind je nach Reaktionsablauf entweder Substrat oder Produkt der Alkoholdehydrogenase). Enzymreaktionen lassen sich durch Bestimmung der Menge des in der Zeiteinheit
gebildeten Produkts oder des verbrauchten Substrats messen. Die reaktionsbeschleunigende Wirkung
von Enzymen wird als Enzymaktivität bezeichnet (Einheiten siehe S. 44).
Enzyme sind Proteine und als solche empfindlich gegen denaturierende Einflüsse (Wärme, Säuren,
Basen etc.). Die Aminosäurensequenz und die räumliche Struktur verschiedener Enzyme sind heute
bekannt. Die Molekularmassen Mr liegen zwischen 104 und 106 (Beispiele: Lysozym 14'400, Phosphorylase a 390'000). Viele, aber nicht alle Enzyme bestehen aus mehreren Peptidketten (Quartärstruktur). Denjenigen Teil eines Enzymmoleküls, an den das Substrat (bzw. Produkt) bindet und wo
die katalytische Umsetzung stattfindet, bezeichnet man als aktive Stelle. Sie umfasst u.a. die an diesen
Prozessen direkt beteiligten Aminosäurereste. Bei gewissen Enzymen enthält die aktive Stelle auch
nicht-proteinartige Bestandteile (prosthetische Gruppen).
Die Geschwindigkeit einer enzymatischen Reaktion hängt von folgenden Reaktionsbedingungen ab.
(1)
(2)
(3)
(4)
(5)
Substratkonzentration
Enzymkonzentration
pH-Wert
Temperatur
Konzentration von Inhibitoren und Aktivatoren
Die Untersuchung der Abhängigkeit der Enzymaktivität von diesen Faktoren ist das Gebiet der
Enzymkinetik.
1. Abhängigkeit der Enzymaktivität von der Substratkonzentration
Im Laufe einer durch ein Enzym E katalysierten Umwandlung von Substrat S in Produkt P entstehen
35
ein Enzym-Substrat-Komplex ES und ein Enzym-Produkt-Komplex EP als Zwischenformen. Die
Reaktionssequenz ist entsprechend:
E + S º ES º EP º E + P
Es ist schwierig, aus diesem allgemein gültigen Schema (6 Teilreaktionen) eine experimentell leicht
nachprüfbare Beziehung zwischen der Reaktionsgeschwindigkeit und der Substratkonzentration
abzuleiten. Zur Vereinfachung beschränkt man sich deshalb auf Bedingungen, unter denen die
Reaktion nur in einer Richtung abläuft, d.h. die Rückwärts-Reaktion (P 6 S) vernachlässigt werden
kann. Dies ist der Fall am Anfang der Reaktion, solange die Konzentration von P verschwindend klein
ist im Vergleich zur Konzentration von S, oder unter Bedingungen, unter denen das Produkt laufend
abgefangen wird. Das Reaktionsschema ist dann:
E + S º ES º EP 6 E + P
Wenn man weiter darauf verzichtet, den ES- und EP-Komplex gesondert zu betrachten (nur die
Geschwindigkeit der ersten Teilreaktion, der Bildung des ES-Komplexes, ist abhängig von der Substratkonzentration), ergibt sich als einfachste Formulierung:
k1
k2
E + S º ES 6 E + P
k-1
wobei k1, k-1 und k2 die Geschwindigkeitskonstanten der Teilreaktionen sind. Aus diesem Schema
lässt sich eine quantitative Beziehung zwischen der Anfangsgeschwindiqkeit v einer enzymatischen
Reaktion und der Substratkonzentration ableiten (Henry, 1903; Michaelis und Menten, 1913; Briggs
und Haldane, 1925).
Die Herleitung ist wie folgt: Die Geschwindigkeit, mit der die Konzentration des Produkts P zunimmt, ist
v =
d[P]
= k2[ES]
dt
(1)
Da v am Anfang der Reaktion, (d.h. solange die Substratkonzentration sich nicht merkbar verändert
hat) konstant bleibt, folgt aus Gleichung (1), dass ES ebenfalls konstant ist. Dies bedeutet, dass die
Bildungs- und Zerfallsgeschwindigkeiten von ES gleich gross sind (= Fliessgleichgewichtszustand).
Die Bildungsgeschwindigkeit von ES ist gleich k1[E]@[S], die Zerfallsgeschwindigkeit gleich k-1[ES]
+ k2[ES]. Daraus folgt:
k1[E][S] = (k-1 + k2)[ES]
(2)
Wir setzen für [E] = [Et]-[ES] ein, wobei [Et] die messbare Gesamtkonzentration des Enzyms darstellt.
Eingesetzt in Gleichung (2) erhalten wir für [ES]
[ES]
=
k1[Et][S]
k-1 + k2 + k1[S]
(3)
Gleichung (3) können wir jetzt in Gleichung (1) einsetzen, d.h. wir drücken die Anfangsgeschwindigkeit der Enzymreaktion als Funktion der gesamten Enzymkonzentration und der Konzentration des
freien Substrats aus:
36
v = k2[ES] =
k2 k1[Et][S]
k-1 + k2 + k1[S]
(4)
Gleichung (4) ist bereits die gesuchte Geschwindigkeitsgleichung für unsere Enzymreaktion, wenn
auch noch nicht in der üblichen Form. Diese erhalten wir, indem wir Zähler und Nenner durch k1
teilen:
k2[Et][S]
v =
k-1 + k2
+ [S]
k1
=
Vmax[S]
(5)
Km + [S]
Dieses ist die Michaelis-Menten-Gleichung. Sie beschreibt die Anfangsgeschwindigkeit einer
Enzymreaktion unter der Annahme des Fliessgleichgewichts. Die Konstanten Km und Vmax sind
definiert als
Km
=
Vmax =
k-1 + k2
k1
k2[Et]
(5a)
(5b)
Km wird Michaeliskonstante genannt. Vmax ist die maximale Geschwindigkeit, die bei der
Konzentration [Et] erreicht werden kann. Sie entspricht dem Zustand, wo alle Enzymmoleküle als
ES vorliegen, also [ES] = [Et]. Weil bei Enzymreaktionen [Et] << [St], kann man in Gleichung (5)
für [S] die Gesamtkonzentration des Substrats einsetzen.
Nach Gleichung (5) ist v eine hyperbolische Funktion von [S].
Abhängigkeit der Aktivität
von der Substratkonzentration
(v gegen [S]-Darstellung)
37
Bedeutung von Km und Vmax:
Die Michaelis-Menten-Gleichung liefert eine Arbeitsdefinition von Km. Km hat die Dimension einer
Konzentration und entspricht numerisch derjenigen Substratkonzentration, bei welcher bei gegebener
Enzymkonzentration die halbmaximale Reaktionsgeschwindigkeit erreicht wird (Substitution von
v = Vmax/2 in Gleichung (5) ergibt Km = [S]). Km kann als reziprokes Mass der "Affinität" von S zu
E aufgefasst werden. Je grösser die Affinität eines Substrats zum Enzym ist, desto kleiner ist die zum
Erreichen der halbmaximalen Umsatzgeschwindigkeit benötigte Substratkonzentration, d.h. ein kleines
Km entspricht einer grossen "Affinität" und umgekehrt. Es muss allerdings betont werden, dass Km
nicht die Dissoziationskonstante Kd = k-1/k1 des Enzym-Substrat-Komplexes darstellt. Wie Gleichung
(5a) zeigt, ist Km durch drei Geschwindigkeitskonstanten bestimmt. Lediglich im Spezialfall k2 <<
k-1 wird der numerische Wert von Km etwa gleich demjenigen von Kd der Reaktion E + S º ES. In
allen andern Fällen ist Km > Kd.
Bei Substratkonzentrationen, die viel kleiner oder grösser sind als Km, ergeben sich folgende
Vereinfachungen der Michaelis-Menten-Beziehung:
[S] << Km :
v =
Vmax@ [S]
Km + [S]
–
Vmax@ [S]
Km
(6)
Da Vmax und Km Konstanten sind, wird v proportional [S], d.h. der enzymatische Prozess verläuft als
Reaktion 1. Ordnung. Gleichung (6) entspricht dem anfänglich linear ansteigenden Abschnitt der
Michalis-Menten-Hyperbel.
[S] >> Km :
v
=
Vmax@ [S]
Km + [S]
– Vmax
(7)
Die Reaktionsgeschwindigkeit wird konstant und unabhängig von [S], d.h. die Umsetzung verläuft
als Reaktion nullter Ordnung. Gleichung (7) entspricht der von der Michaelis-Menten-Hyperbel
angestrebten horizontalen Asymptote.
Bestimmung von Km und Vmax:
Der numerische Wert von Vmax ist bei Anwendung der hyperbolischen v gegen [S]-Darstellung
manuell schwierig zu bestimmen. Die für eine Messung von v in der asymptotisch auslaufenden
Region der Kurve benötigten hohen Substratkonzentrationen sind oft praktisch nicht realisierbar und
Extrapolationen sind unsicher. Die sich daraus ergebende Ungenauigkeit von Vmax erschwert auch
die Bestimmung des Km. Diese Schwierigkeiten werden beseitigt durch Verwendung von
Computerprogrammen, die den Messwerten am besten angepasste Michaelis-Menten-Kurve berechnen
(Hyperbolische Anpassung). Damit erhält man die Werte für Vmax und Km.
Falls keine Rechner zur Verfügung stehen, kann die Michaelis-Menten-Beziehung durch einfache
Umformung von Gleichung (5) in eine linearen Darstellungsform von der Art y = ax + b übergeführt
werden (Darstellung nach Lineweaver-Burk):
38
1
v
1
v
=
=
Km + [S]
Km
=
Vmax@ [S]
Km 1
@
Vmax [S]
Vmax@ [S]
+
[S]
Vmax@ [S]
1
Vmax
+
(8)
Wenn anstelle der gemessenen Werte v und [S] der reziproke Wert 1/v (y-Achse) als Funktion von
1/[S] (x-Achse) graphisch aufgetragen wird, ergibt sich eine Gerade mit der Steigung Km/Vmax. Die
Schnittpunkte mit den Achsen ergeben aufgrund von Gleichung (8)
für die Ordinate (
für die Abszisse (
1
[S]
1
v
= 0):
= 0):
1
v
1
[S]
=
= -
1
Vmax
1
Km
Diese Darstellungsform liefert so durch lineare Extrapolation eindeutige Werte für 1/Vmax
(Ordinatenabschnitt) und -1/Km (Abszissenabschnitt).
Abhängigkeit der Aktivität
von der Substratkonzentration
1
1
(
gegen
-Darstellung)
v
[S]
2. Abhängigkeit der Enzymaktivität von der Enzymkonzentration
Substitution von Vmax = k2 [Et] in Gleichung (5) führt zu
v
=
k2 @ [S]
Km + [S]
@ [Et]
(9)
39
Geschwindigkeit v
d.h. bei gegebener Substratkonzentration ist die Aktivität proportional der Enzymkonzentration
(doppelt soviel Enzymmoleküle können pro Zeiteinheit doppelt soviel Substratmoleküle umsetzen).
Im Gegensatz zu Vmax ist Km unabhängig von der Enzymkonzentration.
Enzymkonzentration
3. Abhängigkeit der Enzymaktivität vom pH
Im allgemeinen ist ein Enzym nur in einem relativ engen pH-Bereich aktiv. Aktivitätsmessungen
müssen deshalb immer unter definierten pH-Bedingungen ausgeführt werden, am einfachsten durch
Verwendung von Pufferlösungen. Als pH-Optimum bezeichnet man den pH-Bereich, an dem die
Aktivität am höchsten ist (z.B. pH 1.5 - 2.5 für Pepsin oder pH 7 - 9 für Trypsin).
Die Lage des pH-Optimums ist durch das Vorhandensein bestimmter ionisierbarer Gruppen am Enzym
oder Substrat erklärbar. In gewissen Fällen können daraus Schlüsse über den Mechanismus der
40
Katalyse gezogen werden (vgl. Reaktionsmechanismus von Chymotrypsin, Exp. 10.1).
4. Abhängigkeit der Enzymaktivität von der Temperatur
Wie andere chemische Reaktionen werden Enzymreaktionen durch Temperaturanstieg beschleunigt.
Aktivitätsmessungen müssen deshalb bei definierter Temperatur ausgeführt werden. Im allgemeinen
findet man bei einer Erhöhung der Temperatur um 10EC eine Aktivitätssteigerung auf etwa das
Doppelte (RGT-Regel). Bei höheren Temperaturen fällt aber die Aktivität wegen der während der
Messung fortschreitenden Hitzedenaturierung des Enzyms wieder ab. Die Temperatur, bei der die
höchste Aktivität gemessen wird, liegt bei den meisten Enzymen zwischen 40EC und 50EC.
5. Wirkung von Inhibitoren und Aktivatoren auf die Enzymaktivität
Für viele Enzyme kennt man spezifische Verbindungen, die die Aktivität entweder herabsetzen
(Inhibitoren) oder steigern (Aktivatoren). Bei den Inhibitoren unterscheidet man dabei solche, die
mit dem Enzym eine irreversible Verbindung eingehen (Beispiel: Hemmung von Chymotrypsin durch
Diisopropylfluorophosphat (DFP)) und solche, die einen reversiblen, d.h. leicht dissoziierbaren
Komplex bilden. Bei den reversiblen Hemmstoffen können als Haupttypen die kompetitiven und
nicht-kompetitiven Inhibitoren unterschieden werden.
Kompetitive Inhibitoren:
Diese hemmen die Bindung des Substrats an das Enzym. Das Ausmass der Hemmung hängt dabei
von den relativen Konzentrationen von Substrat und Inhibitor ab und von ihren relativen Affinitäten
für das Enzym. Wenn Substrat in grossem Überschuss zugegeben wird, verschwindet die Hemmung.
Vmax ist deshalb bei diesem Hemmungstyp nicht verändert. Die Affinität des Substrats zum Enzym
ist aber scheinbar erniedrigt. Der in Gegenwart von Inhibitor gemessene Km-Wert (= K’m) ist grösser
als das Km des nicht gehemmten Enzyms. Spezifische kompetitive Inhibitoren nennt man Inhibitoren,
die dem natürlichen Substrat eines Enzyms strukturell ähnlich sind. So ist z.B. Malonat ein
spezifischer, kompetitiver Inhibitor der Succinatdehydrogenase. Diese Inhibitoren besetzen am Enzym
die gleiche Bindungsstelle wie das Substrat und verhindern so kompetitiv dessen Bindung ans Enzym.
41
Kompetitive Hemmung
Nicht-kompetitive Inhibitoren:
Diese hemmen das Enzym, ohne die Bindung des Substrats zu beeinträchtigen. Umgekehrt hat eine
Steigerung der Substratkonzentration auch keine Wirkung auf die Hemmung. Das Ausmass der
Hemmung hängt nur von der Konzentration des Inhibitors ab. Die mit Inhibitor besetzten EnzymMoleküle sind weniger oder nicht aktiv. Vmax ist deshalb erniedrigt, verglichen mit dem nichtgehemmten Enzym. Der Km-Wert bleibt unverändert.
mit nicht-kompetitivem
Inhibitor
Aktivatoren:
Gewisse Enzyme sind nur aktiv in Gegenwart eines Aktivators oder werden dadurch in ihrer Wirkung
gesteigert. Aktivatoren sind oft bestimmte Ionen, die leicht dissoziierbare Komplexe mit dem Enzym
eingehen, z.B. Mg2+ mit Enolase, Cl- mit Amylasen (Exp. 3.5). Aktivitätsbestimmungen solcher
Enzyme müssen immer in Gegenwart definierter Konzentrationen des Aktivators ausgeführt werden.
H+-Ionen können als Spezialfall sowohl eines Aktivators wie eines Inhibitors betrachtet werden. Die
pH-Abhängigkeit der Enzymwirkung (s. oben) lässt sich in vielen Fällen auf die Aufnahme oder
Abgabe von Protonen durch das Enzym zurückführen. Je nach Enzym ist dabei die protonierte oder
die nicht-protonierte Form die aktive (bzw. aktivere) Spezies.
42
6. Einheiten der Enzymaktivität
Aufgrund von Gleichung (9) ist die Geschwindigkeit einer enzymkatalysierten Reaktion proportional
zur Menge des vorhandenen Enzyms. Die Enzymaktivität wird in Internationalen Einheiten (U)
gemessen. Ein U ist die Enzymaktivität, welche 1 µmol Substrat pro min in Produkt umsetzt.
Die Messung soll bei definierter Temperatur, in der Regel bei 25EC, und optimalen Bedingungen
(Puffer, pH-Wert, Substratkonzentration) ausgeführt werden.
Man beachte, dass U die Dimension einer Geschwindigkeit hat und somit nichts angibt über die
Proteinmenge, in der die Enzymaktivität U enthalten ist.
Die spezifische Aktivität ist die Anzahl Aktivitätseinheiten eines Enzyms pro Menge Protein.
Gewöhnlich wird sie als Anzahl U/mg Protein angegeben. Sie ist ein Mass für den Reinheitsgrad eines
Enzympräparates. Die spezifische Aktivität steigt im Laufe der Reindarstellung eines Enzyms durch
sukzessive Entfernung aller Fremdproteine bis zu dem für das reine Enzym typischen maximalen
Wert an. Wenn das Enzym rein und seine Molekularmasse bekannt ist, lässt sich die molekulare
Aktivität berechnen. Sie wird angegeben als Anzahl U/µmol Enzym. Die molekulare Aktivität (oder
Wechselzahl) des Enzyms gibt die Anzahl Substratmoleküle an, welche bei optimaler Substratkonzentration durch 1 Enzymmolekül pro min umgesetzt wird. Die Wechselzahl vieler Enzyme liegt
zwischen 103 und 104 min-1.
Der optische Test (nach Warburg S. 20)
Die reduzierten Pyridinnucleotide NADH bzw. NADPH zeigen bei 340 nm eine Absorptionsbande,
die den oxidierten Formen fehlt (S. 20 und Exp. 1.7). Die Umwandlung der reduzierten in die
oxidierten Formen und umgekehrt lässt sich deshalb durch Extinktionsmessungen verfolgen. Diese
Eigenschaft erlaubt die Messung von enzymkatalysierten Reaktionen, an denen PyridinnucleotidCoenzyme beteiligt sind.
Alle Reaktionen dieser Art verlaufen nach dem Schema:
Dehydrogenase
+
H2R + NAD(P)
º
R + NAD(P)H + H+
wobei H2R und R je nach Reaktionsrichtung das Substrat bzw. das Produkt darstellen. Die Mengen
von umgesetztem Substrat und Coenzym sind gleich. Die optisch messbare Konzentrationsänderung
(Zunahme oder Abnahme) des reduzierten Coenzyms ist deshalb ein direktes Mass für das verbrauchte
Substrat oder gebildete Produkt. Die Konzentration von NADH bzw. NADPH lässt sich aufgrund
des Beer-Lambert-Gesetz (S. 31) aus Extinktionsmessungen im Bereich der DihydronicotinamidAbsorptionsbande des Coenzyms ermitteln. Bei Verwendung eines Spektralphotometers erfolgt die
Messung am Absorptionsmaximum (340 nm) unter Anwendung des millimolaren Extinktionskoeffizienten, ε340 = 6.22. Bei Photometern, die mit einer Hg-Dampflampe (diskontinuierliches
Linienspektrum) ausgerüstet sind, steht nur die Emissionslinie von Hg bei 365 nm zur Verfügung.
Da diese Wellenlänge nicht dem Absorptionsmaximum entspricht, muss der niedrigere Extinktionskoeffizient ε365,mM = 3.3 verwendet werden. Je nach Wahl der Versuchsbedingungen kann der optische
Test zur Messung von Enzymaktivitäten oder zur enzymatischen Bestimmung von Substratkonzentrationen verwendet werden (Exp. 1.7 und 1.9, bzw. Exp. 8.1 und 8.3 Naturwissenschafter).
43
7. Bestimmung von Enzymaktivitäten im optischen Test
Die gesuchte Grösse ist die Anzahl Enzymaktivitätseinheiten pro ml der verwendeten Enzymlösung
(Anzahl U/ml) oder die spezifische Aktivität (Anzahl U/mg) des Enzyms. Es ist vorteilhaft, zuerst
die Anzahl U/ml im Reaktionsansatz (in der Küvette) zu ermitteln und dann den gefundenen Wert
unter Berücksichtigung des Verdünnungsfaktors auf die Anzahl U/ml in der verwendeten
Enzymlösung umzurechnen. Aus dieser Grösse und der Proteinkonzentration der Enzymlösung
(mg/ml) erhält man die spezifische Aktivität des Enzyms in U/mg.
Die Enzymaktivität pro ml im Ansatz ist die pro ml und pro min umgesetzte Anzahl µmol NADH.
µmol NADH
Anzahl U/ml im Ansatz =
min @ ml
(1)
Die Konzentrationsänderung von NADH pro min ist bei Messung in einer Küvette von 1 cm Schichtdicke die in der Minute erfolgte Änderung der Extinktion (∆E340/min) dividiert durch den millimolaren
Extinktionskoeffizienten ε340 = 6.22. Die Enzymaktivität ist somit:
Anzahl U/ml im Ansatz =
∆E340
ε340 @ min
(1a)
Die Anzahl U/ml in der zum Ansatz zugegebenen Enzymlösung erhält man durch Multiplikation der
aus Gleichung (1a) erhaltenen Aktivitätskonzentration mit dem Verdünnungsfaktor:
Anzahl U/ml der Enzymlösung = Anzahl U/ml Ansatz @ Verdünnungsfaktor
Der Verdünnungsfaktor beträgt:
Volumen des Ansatzes
(2)
(2a)
Volumen der zugegebenen Enzymlösung
Die spezifische Aktivität U/mg ist die Aktivitätskonzentration der Enzymlösung (U/ml) dividiert durch
die Proteinkonzentration der Enzymlösung (mg/ml):
Spezifische Aktivität =
Anzahl U/ml der Enzymlösung
mg Protein pro ml Enzymlösung
(3)
Beispiel:
Eine Lösung von Isocitratdehydrogenase (5 mg/ml) wird 1:200 mit H2O verdünnt und 50 µl davon
werden zum optischen Test verwendet, der in einem Totalvolumen von 3.00 ml ausgeführt wird (Verdünnungsfaktor = 12'000). Es wird eine Extinktionsabnahme bei 340 nm von 0.53 pro min gemessen.
Aufgrund von ε340 = 6.22 mM-1cm-1 ist die Aktivitätskonzentration im Ansatz 0.53/6.22 = 0.085 U/ml.
In der verwendeten Enzymlösung ist die Aktivitätskonzentration = 12'000 x 0.085 = 1020 U/ml und
die spezifische Aktivität = 1020/5 = 204 U/mg.
44
Bestimmung von Substratkonzentrationen durch einen optischen Test
Unter Reaktionsbedingungen, bei denen im Gleichgewichtszustand das Verhältnis von Produkt zu
Substrat sehr gross ist, oder wenn das gebildete Produkt durch eine weitere Reaktion laufend aus dem
Gleichgewicht entfernt wird, wird zum Ansatz zugegebenes Substrat praktisch quantitativ in Produkt
umgesetzt. Die Menge des gebildeten Produkts und des in der Reaktion ebenfalls umgesetzten
Coenzyms ist dann ein Mass für die ursprünglich zugegebene Menge von Substrat. Die umgesetzte
Menge Coenzym lässt sich im optischen Test aus der maximal erzielten Extinktionsänderung, ∆E340,
ermitteln gemäss:
Konzentration des Substrats im Ansatz =
∆E340
ε340,mM
(4)
Die gesuchte millimolare Konzentration der zum Ansatz zugegebenen Substratlösung [S0] erhält man
durch Multiplikation der aus Gleichung (4) erhaltenen Konzentration mit dem Verdünnungsfaktor
[So] =
∆E340
ε340, mM
@ Verdünnungsfaktor
(5)
Beispiel:
In einem Ansatz vom Volumen 3.0 ml, der 0.15 ml einer Pyruvatlösung unbekannter Konzentration
und einen Überschuss an NADH enthält, wird nach Zugabe von Lactatdehydrogenase eine maximale
Extinktionsabnahme ∆E340 = 0.59 gemessen. Die anfängliche Substratkonzentration im Ansatz beträgt
0.59/6.22 = 0.095 mM. Die gesuchte Konzentration der Pyruvatlösung beträgt 1.90 mM (Verdünnungsfaktor = 20). Bei einer Molekularmasse von 88 Da für Pyruvat beträgt die Massenkonzentration der Pyruvatlösung 1.90 x 88 = 167.2 µg/ml.