Zusammenfassung: Komplexe Zahlen - Lehrer-Uni
Werbung
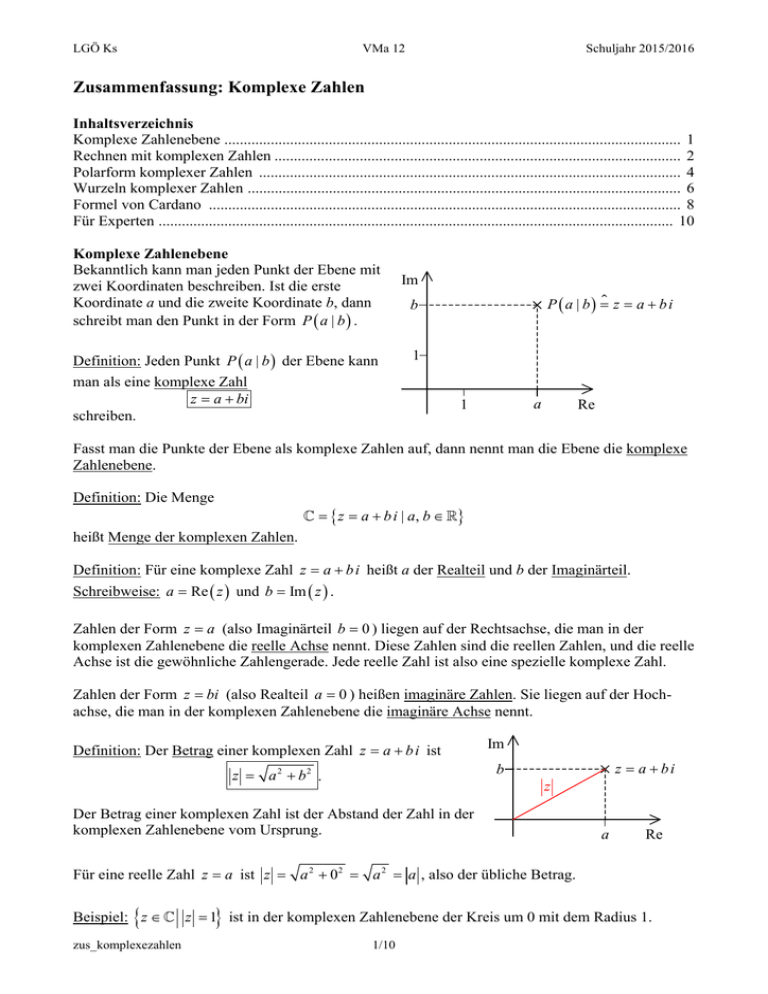
LGÖ Ks VMa 12 Schuljahr 2015/2016 Zusammenfassung: Komplexe Zahlen Inhaltsverzeichnis Komplexe Zahlenebene ...................................................................................................................... 1 Rechnen mit komplexen Zahlen ......................................................................................................... 2 Polarform komplexer Zahlen ............................................................................................................. 4 Wurzeln komplexer Zahlen ................................................................................................................ 6 Formel von Cardano .......................................................................................................................... 8 Für Experten ..................................................................................................................................... 10 Komplexe Zahlenebene Bekanntlich kann man jeden Punkt der Ebene mit zwei Koordinaten beschreiben. Ist die erste Koordinate a und die zweite Koordinate b, dann schreibt man den Punkt in der Form P a | b . Definition: Jeden Punkt P a | b der Ebene kann Im P a | b z a b i b 1 man als eine komplexe Zahl z a bi schreiben. a 1 Re Fasst man die Punkte der Ebene als komplexe Zahlen auf, dann nennt man die Ebene die komplexe Zahlenebene. Definition: Die Menge z a b i | a, b heißt Menge der komplexen Zahlen. Definition: Für eine komplexe Zahl z a b i heißt a der Realteil und b der Imaginärteil. Schreibweise: a Re z und b Im z . Zahlen der Form z a (also Imaginärteil b 0 ) liegen auf der Rechtsachse, die man in der komplexen Zahlenebene die reelle Achse nennt. Diese Zahlen sind die reellen Zahlen, und die reelle Achse ist die gewöhnliche Zahlengerade. Jede reelle Zahl ist also eine spezielle komplexe Zahl. Zahlen der Form z bi (also Realteil a 0 ) heißen imaginäre Zahlen. Sie liegen auf der Hochachse, die man in der komplexen Zahlenebene die imaginäre Achse nennt. Definition: Der Betrag einer komplexen Zahl z a b i ist Im z a bi b z a 2 b2 . z Der Betrag einer komplexen Zahl ist der Abstand der Zahl in der komplexen Zahlenebene vom Ursprung. a Re Für eine reelle Zahl z a ist z a 2 02 a 2 a , also der übliche Betrag. Beispiel: z z 1 ist in der komplexen Zahlenebene der Kreis um 0 mit dem Radius 1. zus_komplexezahlen 1/10 LGÖ Ks VMa 12 Schuljahr 2015/2016 Im Definition: Für eine komplexe Zahl z a b i heißt z a bi die konjugiert komplexe Zahl. z a bi b Die konjugiert komplexe Zahl entsteht durch eine Spiegelung an der reellen Achse. a z a bi –b Re Für eine reelle Zahl ist die konjugiert komplexe Zahl gleich der Zahl selbst. Rechnen mit komplexen Zahlen Definition (Addition): a b i c d i a c b d i Deutung in der komplexen Zahlenebene: Den komplexen Zahlen z a b i und w c d i entsprechen die Punkte P a | b und Q c | d mit den a c Ortsvektoren OP und OQ . b d Der Summe z w entspricht der Punkt mit dem Orts a c vektor OP OQ . b d Im zw w z Re Für reelle Zahlen z a 0 i und w c 0 i ist z w a c 0 i a c , also die übliche Addition. Feststellung: Für die Addition komplexer Zahlen gilt: 1. das Kommutativgesetz: z1 z2 z2 z1 ; 2. das Assoziativgesetz: z1 z2 z3 z1 z2 z3 ; 3. es gibt ein neutrales Element: z 0 z ; 4. jede Zahl z a b i hat eine Gegenzahl, nämlich z a b i , so dass gilt: z z 0 . Für eine reelle Zahl z a ist die Gegenzahl z a , also die übliche Gegenzahl. Im z a bi b Das Negative einer komplexen Zahl entsteht durch eine Spiegelung am Ursprung. –a a –b z a b i Wie bei reellen Zahlen wird die Subtraktion definiert als die Addition der Gegenzahl: Definition (Subtraktion): z w z w Also ist a b i c d i a c b d i . zus_komplexezahlen 2/10 Re LGÖ Ks VMa 12 Schuljahr 2015/2016 Der Abstand zweier reeller Zahlen a und b auf der Zahlengeraden ist a b . Das gilt entsprechend für komplexe Zahlen: Merke: Der Abstand zweier komplexer Zahlen z und w in der komplexen Zahlenebene ist zw . Beispiel: z z i 1 ist in der komplexen Zahlenebene der Kreis um i mit dem Radius 1. Definition (Multiplikation): a b i c d i ac bd ad bc i . Beispiel: i i 0 1i 0 1i 0 0 1 1 0 1 1 0 i 1 Für reelle Zahlen z a 0 i und w c 0 i ist z w a 0 i c 0 i ac 0 0 a 0 0 c a c , also die übliche Multiplikation. Feststellung: Für die Multiplikation komplexer Zahlen gilt: 1. das Kommutativgesetz: z1 z2 z2 z1 ; 2. das Assoziativgesetz: z1 z2 z3 z1 z2 z3 ; 3. es gibt ein neutrales Element: z 1 z . Feststellung: Für die Addition und die Multiplikation komplexer Zahlen gilt das Distributivgesetz: z1 z2 z3 z1 z2 z1 z3 . Tatsächlich muss man sich die Definition der Multiplikation nicht merken, sondern man schreibt die komplexen Zahlen in Klammern, multipliziert wie üblich aus und ersetzt i i durch 1 . Beispiel: 2 3 i 4 5 i 2 4 2 5 i 3 i 4 3 i 5 i 8 10 i 12 i 15 ii 8 22 i 15 7 22 i Definition (n-te Potenz): z n z z z ( n 1, 2, 3, ) n Faktoren 2 Beispiel: i i i 1 Feststellung: Jede komplexe Zahl z a b i , z 0 hat eine Kehrzahl, nämlich 1 a b 2 2 i, 2 z a b a b2 1 so dass gilt: z 1 . z Beweis: Es ist a bi a b , also i 2 2 2 2 a b a b a b2 2 2 a b i a b i a b i a b i 1 a 2 b2 z a bi 2 1. z a b2 a 2 b2 a 2 b2 a 2 b2 2 zus_komplexezahlen 3/10 LGÖ Ks VMa 12 Bemerkung: Es ist Schuljahr 2015/2016 1 z 1 z zz 1 2 2 , also z z 2 2 . Wegen z z z ist z 1 . z z z z z z Für eine reelle Zahl z a ist Definition (Division): 1 a 1 , also die übliche Kehrzahl. z a2 a z 1 z (w 0) w w Diese Definition ergibt für reelle Zahlen die übliche Division. Tatsächlich muss man sich die Definition der Division nicht merken, sondern man erweitert den Bruch mit dem komplex konjugierten Nenner und wendet die dritte binomische Formel an. Beispiel: 4 5 i 4 5 i 6 8 i 24 32 i 30 i 40 64 2 i 64 2 16 1 i i 6 8i 6 8i 6 8i 36 64 100 100 100 25 50 Für Experten: Die komplexen Zahlen bilden einen Körper. Polarform komplexer Zahlen Feststellung und Definition: Jeder komplexen Zahl z 0 kann man den Winkel zwischen der positiven reellen Achse und der Strecke 0z zuordnen, wobei 180 180 gilt. Dieser Winkel heißt das Argument von z. Schreibweise: arg z Beispiel: arg i 90 Berechnung von arg z : Sonderfälle: 1. z reell, also z a : a) a 0 : 0 b) a 0 : 180 2. z imaginär, also z b i : c) b 0 : 90 d) b 0 : 90 Im Allgemeiner Fall: Für z a bi ist b tan . a z a bi b b a zus_komplexezahlen 4/10 a Re Im z 0 Re LGÖ Ks VMa 12 Schuljahr 2015/2016 Achtung: Im Fall 1. a 0 und b 0 ist 90 180 , und man muss 180° zum GTR-Ergebnis addieren. Beispiel: z 3 2 i 2 2 tan 3 3 33, 7 180 146,3 2. a 0 und b 0 ist 180 90 , und man muss 180° vom GTR-Ergebnis subtrahieren. Beispiel: z 3 2 i 2 2 tan 3 3 33, 7 180 146,3 Eine komplexe Zahl z a b i , z 0 kann man mit ihrem Betrag r z und ihrem Argument arg z darstellen: Im Im Sonderfall r 1 (Vergleiche „Sinus und Kosinus im Einheitskreis“) gilt a cos 1 b z a bi b sin a 1 Re Im r z a bi b Im allgemeinen Fall mit beliebigem r denkt man sich das obige Bild zentrisch gestreckt, mit dem Ursprung als Streckzentrum und dem Streckfaktor r. Dann erhält man a r cos r Re a b r sin r Also gilt z a b i r cos r sin i r cos sin i . Das ist die Darstellung mit dem Betrag und dem Argument: Definition: Die Polarform einer komplexen Zahl z 0 ist z r cos sin i mit r z und arg z . Bemerkung: Der GTR stellt die Polarform in der Form z r e i dar. Im Gegensatz zur Polarform heißt die Darstellung z a b i die Normalform. zus_komplexezahlen 5/10 LGÖ Ks VMa 12 Schuljahr 2015/2016 Umrechnung von der Normalform z a b i in die Polarform z r cos sin i : 1. r z a 2 b 2 2. Bestimme arg z wie oben erläutert. Umrechnung von der Polarform z r cos sin i in die Normalform z a bi : z r cos r sin i , also a r cos und b r sin . Feststellung (Beweis siehe „Für Experten“): Für komplexe Zahlen z1 r1 cos 1 sin 1 i und z2 r2 cos 2 sin 2 i ist z1 z2 r1 r2 cos 1 2 sin 1 2 i . Also gilt: z1 z2 z1 z2 und arg z1 z2 arg z1 arg z2 Für Experten: Man muss evtl. 360° addieren oder subtrahieren. Merke: Bei der Multiplikation komplexer Zahlen multiplizieren sich die Beträge und addieren sich die Argumente. Durch n-fache Anwendung dieser Formel bzw. durch vollständige Induktion folgt der Satz (Formel von Moivre): Die n-te Potenz ( n 2, 3, 4, ) einer komplexen Zahl z r cos sin i ist z n r n cos n sin n i . Also gilt: n z n z arg z n n arg z Für Experten: Man muss eventuell 360° oder ein Vielfaches von 360° addieren oder subtrahieren. Wurzeln komplexer Zahlen Definition: Gegeben ist eine komplexe Zahl z und eine natürliche Zahl n 2 . Eine komplexe Zahl w mit wn z heißt eine n-te Wurzel von z; im Fall n 2 heißt w eine Quadratwurzel von z. Liest man die Formel von Moivre „rückwärts“, dann erhält man den Satz: Jede komplexe Zahl z hat eine n-te Wurzel ( n 2, 3, 4, ), nämlich die Zahl w, für die gilt: w zus_komplexezahlen n z und arg w 6/10 arg z n . LGÖ Ks Also ist Re w VMa 12 n arg z z cos und Im w n n Schuljahr 2015/2016 arg z z sin . n Standardaufgabe: Berechne eine n-te Wurzel w einer komplexen Zahl z a bi . Lösung: 1. Berechne z a 2 b 2 . 2. Berechne tan arg z b a arg z Achtung: Im Fall a 0 und b 0 muss man 180° zum GTR-Ergebnis addieren, und im Fall a 0 und b 0 muss man 180° vom GTR-Ergebnis subtrahieren! arg z arg z 3. Berechne Re w n z cos und Im w n z sin . n n Feststellung: Ist die Zahl w1 eine n-te Wurzel der Zahl z ( n 2, 3, 4, ), dann erhält man eine 360 weitere n-te Wurzel w2 von z, indem man das Argument von w1 um vergrößert. n Beweis: Da w1 eine n-te Wurzel von z ist, gilt n arg w1 arg z . Daraus folgt 360 n arg w2 n arg w1 n arg w1 360 n arg w1 arg z . n Also ist auch w2 eine n-te Wurzel von z. Folgerung: Eine komplexe Zahl z 0 hat für jede natürliche Zahl n 2 mindestens n verschiedene n-te Wurzeln. 360 erhöhen, bis man das n ursprüngliche Argument plus 360° und damit die ursprüngliche n-te Wurzel erhält. Beweis: Man kann das Argument einer n-ten Wurzel n-mal um Feststellung: Eine komplexe Zahl z hat für jede natürliche Zahl n 2 höchstens n verschieden n-te Wurzeln. Beweis: Eine n-te Wurzel von z ist eine Nullstelle des Polynoms x n z 0 , und wie im Reellen hat ein Polynom vom Grad n höchstens n Nullstellen. Daraus folgt der Satz: Eine komplexe Zahl z 0 hat für jede natürliche Zahl n 2 genau n verschiedene n-te Wurzeln. Bei reellen Zahlen ist das bekanntlich anders: 1. Eine positive reelle Zahl x hat genau eine reelle n-te Wurzel, nämlich n x . 2. Ist x eine negative reelle Zahl und n ungerade, dann hat x genau eine reelle n-te Wurzel, nämlich n x . zus_komplexezahlen 7/10 LGÖ Ks VMa 12 Schuljahr 2015/2016 3. Ist x eine negative reelle Zahl und n gerade, dann hat x keine n-te Wurzel. Fall n 2 : Eine komplexe Zahl z 0 hat zwei verschiedene Quadratwurzeln: arg z 1. Die Zahl w1 mit w1 z und arg w1 ; 2 2. die Zahl w2 w1 . Sonderfall: Eine negative reelle Zahl x hat die beiden Quadratwurzeln w1 x i und w2 x i . Beispiel: Die Zahl 1 hat die beiden Quadratwurzeln i und i . Alle n-ten Wurzeln einer komplexen Zahl z haben denselben Betrag unterscheiden sich jeweils um n z , und ihre Argumente 360 . Daraus folgt die n Feststellung: Die n-ten Wurzeln einer komplexen Zahl z liegen in der Zahlenebene auf dem Kreis um den Ursprung mit dem Radius n z , und sie sind die Eckpunkte eines regelmäßigen n-Ecks. Im Beispiel: Die vierten Wurzeln von 1 sind i, 1 , i und 1. Sie liegen auf dem Einheitskreis und sind die Ecken eines Quadrats. 1 i 1 Re –1 –i Feststellung: Ist die Zahl w eine n-te Wurzel der Zahl z, dann ist w eine n-te Wurzel von z . 2 Beweis: Da w eine n-te Wurzel von z ist, gilt wn z . Man kann nachrechnen, dass w w2 gilt. n n Daraus folgt durch vollständige Induktion: w wn . Also ist w z , d. h. w ist eine n-te Wurzel von z . Formel von Cardano Eine Gleichung dritten Grades, also eine Gleichung der Form ax 3 bx 2 cx d 0 ( a, b, c, d ; a 0 ), hat stets eine reelle Zahl als Lösung, denn fasst man die linke Seite als den Term einer Funktion f auf, dann ist f eine Funktion dritten Grades, für die gilt: 1. Fall a 0 : Für x strebt f x , und für x strebt f x ; 2. Fall a 0 : Für x strebt f x , und für x strebt f x . Also hat f auf jeden Fall eine (reelle) Nullstelle, d. h. die Gleichung hat eine reelle Lösung. Für eine spezielle Form einer solchen Gleichung gibt es eine Lösungsformel: zus_komplexezahlen 8/10 LGÖ Ks VMa 12 Schuljahr 2015/2016 Satz (Formel von Cardano; ohne Beweis): Gegeben ist eine Gleichung der Form x3 px q 0 ( p, q ). Bei geeigneter Wahl der Wurzeln ist 3 p q mit D 3 2 q q x D 3 D 2 2 eine reelle Lösung der Gleichung. 3 2 Es gibt zwei Fälle: 1. Ist D 0 , dann ist D eine reelle Zahl, und bei der Berechnung der Lösung treten nur reelle Zahlen auf, weil man als dritte Wurzel einer reellen Zahl immer eine reelle Zahl nehmen kann. 2. Ist D 0 , dann ist D D i. Setzt man z : q D 2 dann lautet die Formel von Cardano: x3z 3 z . Ist w eine dritte Wurzel von z, dann ist w eine dritte Wurzel von z . Also ergibt die Formel von Cardano die Lösung x w w. Die Zahl x ist eine reelle Zahl, denn für jede komplexe Zahl w a b i ist w w a b i a b i 2a 2 Re w . Standardaufgabe: Bestimme eine reelle Lösung der Gleichung x3 px q 0 . Lösung: 3 2 p q 1. Berechne D . 3 2 2. Fall D 0 : Berechne x 3 q q D3 D. 2 2 Fall D 0 : 3. Berechne z q D mit 2 D 4. Berechne den Realteil Re w 5. Berechne x 2 Re w . 3 D i. arg z z cos einer dritten Wurzel w von z. 3 Für Experten: Eine Gleichung der Form x3 bx 2 cx d 0 ( b, c, d ) kann durch eine geeignete Substitution in eine Gleichung der Form u 3 pu q 0 überführt werden. Also kann man mit der Formel von Cardano beliebige Gleichungen dritten Grades lösen. zus_komplexezahlen 9/10 LGÖ Ks VMa 12 Schuljahr 2015/2016 Für Experten Beweis der Feststellung: Für komplexe Zahlen z1 r1 cos 1 sin 1 i und z2 r2 cos 2 sin 2 i gilt z1 z2 r1 r2 cos 1 2 sin 1 2 i . Beweis: Ohne Begründung: Additionstheoreme für Sinus und Kosinus: sin sin cos cos sin cos cos cos sin sin Daraus folgt z1 z2 r1 cos 1 sin 1 i r2 cos 2 sin 2 i r1 r2 cos 1 cos 2 sin 1 sin 2 cos 1 sin 2 sin 1 cos 2 i r1 r2 cos 1 2 sin 1 2 i Feststellung: Eine Gleichung der Form x3 bx 2 cx d 0 ( b, c, d ) wird durch die Substitution b xu 3 in eine Gleichung der Form u 3 pu q 0 überführt. Beweis: Die Substitution ergibt 3 2 b b b u b u c u d 0 3 3 3 2 2 b2 bc b b b u 3 u 3 u b u ub cu d 0 3 9 3 3 3 3 b2 b3 b3 bc 2 u 3 bu 2 u bu 2 b 2 u cu d 0 3 27 3 9 3 2 b bc 2 u 3 c u b3 d 0 3 27 3 2 3 zus_komplexezahlen 3 2 10/10