3. Schriftliche Wiederholung aus Physik Donnerstag, 27. Februar 1997
Werbung

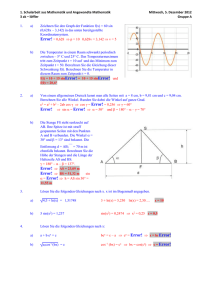
2. Schularbeit aus Mathematik und angewandter Mathematik 2 ak - hall 1. a) Mittwoch, 22. März 2017 Gruppe A Ein Haus mit asymmetrischem Dach (siehe Skizze) hat auf der linken Seite eine Dachneigung von = 30°. Das Haus hat –– eine Breite von AB; = 40 m. Die Länge der Dachsparren –– AC; auf der linken Seite beträgt 15 m. –– - Berechnen Sie die Firsthöhe FC; . –– –– - Berechnen Sie die Entfernungen AF; und FB; und den Winkel . cos = Error! x = s cos = 12,99 m. sin = Error! h = s sin = 7,50 m tan = Error! = arctan Error! = 15,5° Die Firsthöhe ist 7,50 m, der Fußpunkt F steht in einer Entfernung von 12,99 m rechts von A und 27,01 m links von B, die Dachneigung auf der flachen Seite ist 15,5°. b) Ein Teil einer Schipiste zwischen den Punkten A und B hat eine Hangneigung von = 60°. Die Seehöhe von A beträgt 2 120 m, die von B 1 920 m. –– - Berechnen Sie die Länge der Strecke AB; . Rennfahrerinnen bewegen sich auf diesem Abschnitt mit ca. 108 km/h = 30 m/s. - Berechnen Sie, wie lange sich die Rennläuferin auf diesem Abschnitt befindet. Der Abschnitt nach B verläuft wesentlich flacher und hat eine Hangneigung von 28°. Unter Steigung versteht man das Verhältnis von Höhendifferenz zu waagrechter Entfernung. - Berechnen Sie die Steigung dieses Abschnitts. sin = Error! s = Error! = 230,94 m tan = Error! = Steigung = 53,2 % 2. a) Ergänzen Sie die folgenden Formeln für die nebenstehende Figur: cos = b) t = Error! = 7,7 s Error! Error! = tan sin(90° – ) = Error! In einem normal beschrifteten rechtwinkeligen Dreieck kennt man die Fläche A = 52 cm2 und die Länge der Seite a = 8 cm. - Berechnen Sie die beiden nicht rechten Winkel und die Länge der Hypotenuse c A = Error! b = Error! = 13 Error! = 31,6° = 90° – = 58,4° c = Error! = 15,26 cm tan = Error! = arctan A 3. a) Zwei Schiffe fahren gleichzeitig von einem Hafen weg. Schiff A bewegt sich mit der Geschwindigkeit 20 Knoten (kn) (= Seemeilen pro Stunde Nm/h) mit Kurs 60 vom Hafen weg. Schiff B fährt 18 kn mit Kurs 130. - Zeichnen Sie eine Skizze für diese Situation. Die Kursangabe 60 bedeutet, dass der Winkel zur Nordrichtung 60° ist (im Uhrzeigersinn gemessen) - Berechnen Sie die Entfernung der beiden Schiffe in Seemeilen (nautical miles Nm) nach 5 Stunden. e2 = (5 · 20)2 + (5 · 18)2 – 2 · 5 · 20 · 5 · 18 cos(130° – 60°) e = 109,3 Nm 4. b) Geben Sie für die nebenstehende Situation eine Formel für h an, wenn ϵ, und d gegeben sind. tan = Error! x = d tan tan(ϵ – ) = Error! y = d tan (ϵ – ) h = d tan + d tan (ϵ – ) a) In einem allgemeinen normbeschrifteten Dreieck kennt man die Seiten a = 10 cm, b = 8 cm und die Größe des Winkels = 50°. - Berechnen Sie die Länge der Seite c und die Größe der anderen Winkel. Error! = Error! sin = Error! = 73,25° γ = 180° – – = 56,75° Error! = Error! c = Error! = 8,73 cm b) Ein Grundstück ist trapezförmig und man kennt man die Länge h = 300 m und b = 500 m und die Winkel ∠ DAB = 90°, ∠ ABC = 90° und ∠ ADC = 109,8°. - Berechnen Sie die Fläche des Grundstücks. = 109,8° – 90° = 19,8° tan = Error! x = b tan = 180 m A = hb + Error! = 150 000 + 45 000 = 195 000 m2 2. Schularbeit aus Mathematik und angewandter Mathematik 2 ak - hall 1. a) Mittwoch, 22. März 2017 Gruppe B Ein Haus mit asymmetrischem Dach (siehe Skizze) hat auf der linken Seite eine Dachneigung von = 40°. Das Haus hat –– eine Breite von AB; = 40 m. Die Länge der Dachsparren –– AC; auf der linken Seite beträgt 15 m. –– - Berechnen Sie die Firsthöhe FC; . –– –– - Berechnen Sie die Entfernungen AF; und FB; und den Winkel . cos = Error! x = s cos = 11,49 m. sin = Error! h = s sin = 9,64 m tan = Error! = arctan Error! = 18,7° Die Firsthöhe ist 9,64 m, der Fußpunkt F steht in einer Entfernung von 11,49 m rechts von A und 28,51 m links von B, die Dachneigung auf der flachen Seite ist 18,7°. b) Ein Teil einer Schipiste zwischen den Punkten A und B hat eine Hangneigung von = 50°. Die Seehöhe von A beträgt 2 120 m, die von B 1 920 m. –– - Berechnen Sie die Länge der Strecke AB; . Rennfahrerinnen bewegen sich auf diesem Abschnitt mit ca. 108 km/h = 30 m/s. - Berechnen Sie, wie lange sich die Rennläuferin auf diesem Abschnitt befindet. Der Abschnitt nach B verläuft wesentlich flacher und hat eine Hangneigung von 20°. Unter Steigung versteht man das Verhältnis von Höhendifferenz zu waagrechter Entfernung. - Berechnen Sie die Steigung dieses Abschnitts. sin = Error! s = Error! = 261,08 m tan = Error! = Steigung = 36,4 % 2. a) Ergänzen Sie die folgenden Formeln für die nebenstehende Figur: sin = b) t = Error! = 8,7 s Error! Error! = tan cos(90° – ) = Error! In einem normal beschrifteten rechtwinkeligen Dreieck kennt man die Fläche A = 26 cm2 und die Länge der Seite a = 4 cm. - Berechnen Sie die beiden nicht rechten Winkel und die Länge der Hypotenuse c A = Error! b = Error! = 13 Error! = 17,1° = 90° – = 72,9° c = Error! = 13,60 cm tan = Error! = arctan B 3. a) Zwei Schiffe fahren gleichzeitig von einem Hafen weg. Schiff A bewegt sich mit der Geschwindigkeit 20 Knoten (kn) (= Seemeilen pro Stunde Nm/h) mit Kurs 60 vom Hafen weg. Schiff B fährt 18 kn mit Kurs 140. - Zeichnen Sie eine Skizze für diese Situation. Die Kursangabe 60 bedeutet, dass der Winkel zur Nordrichtung 60° ist (im Uhrzeigersinn gemessen) - Berechnen Sie die Entfernung der beiden Schiffe in Seemeilen (nautical miles Nm) nach 5 Stunden. e2 = (5 · 20)2 + (5 · 18)2 – 2 · 5 · 20 · 5 · 18 cos(140° – 60°) e = 122,3 Nm 4. b) Geben Sie für die nebenstehende Situation eine Formel für h an, wenn ϵ, und d gegeben sind. tan = Error! x = d tan tan(ϵ – ) = Error! y = d tan (ϵ – ) h = d tan + d tan (ϵ – ) a) In einem allgemeinen normbeschrifteten Dreieck kennt man die Seiten a = 5 cm, b = 4 cm und die Größe des Winkels = 50°. - Berechnen Sie die Länge der Seite c und die Größe der anderen Winkel. Error! = Error! sin = Error! = 73,25° γ = 180° – – = 56,75° Error! = Error! c = Error! = 4,37 cm b) Ein Grundstück ist trapezförmig und man kennt man die Länge h = 300 m und b = 500 m und die Winkel ∠ DAB = 90°, ∠ ABC = 90° und ∠ ADC = 111,8°. - Berechnen Sie die Fläche des Grundstücks. = 111,8° – 90° = 21,8° tan = Error! x = b tan = 200 m A = hb + Error! = 150 000 + 50 000 = 200 000 m2 2. Schularbeit aus Mathematik und angewandter Mathematik 2 ak - hall 1. a) b) Mittwoch, 22. März 2017 Gruppe A Ein Haus mit asymmetrischem Dach (siehe Skizze) hat auf der linken Seite eine Dachneigung von = 30°. –– Das Haus hat eine Breite von AB; = 40 m. –– Die Länge der Dachsparren AC; auf der linken Seite beträgt 15 m. –– Berechnen Sie die Firsthöhe FC; . –– –– Berechnen Sie die Entfernungen AF; und FB; und den Winkel . Ein Teil einer Schipiste zwischen den Punkten A und B hat eine Hangneigung von = 60°. Die Seehöhe von A beträgt 2 120 m, die von B 1 920 m. –– - Berechnen Sie die Länge der Strecke AB; . Rennfahrerinnen bewegen sich auf diesem Abschnitt mit ca. 108 km/h = 30 m/s. - Berechnen Sie, wie lange sich die Rennläuferin auf diesem Abschnitt befindet. Der Abschnitt nach B verläuft wesentlich flacher und hat eine Hangneigung von 28°. Unter Steigung versteht man das Verhältnis von Höhendifferenz zu waagrechter Entfernung. - Berechnen Sie die Steigung dieses Abschnitts. - A 2. a) Ergänzen Sie die folgenden Formeln für die nebenstehende Figur: cos = Error! = sin(90° – ) = b) In einem normal beschrifteten rechtwinkeligen Dreieck kennt man die Fläche A = 52 cm2 und die Länge der Seite a = 8 cm. - Berechnen Sie die beiden nicht rechten Winkel und die Länge der Hypotenuse c A 3. a) Zwei Schiffe fahren gleichzeitig von einem Hafen weg. Schiff A bewegt sich mit der Geschwindigkeit 20 Knoten (kn) (= Seemeilen pro Stunde Nm/h) mit Kurs 60 vom Hafen weg. Schiff B fährt 18 kn mit Kurs 130. - Zeichnen Sie eine Skizze für diese Situation. Die Kursangabe 60 bedeutet, dass der Winkel zur Nordrichtung 60° ist (im Uhrzeigersinn gemessen) - Berechnen Sie die Entfernung der beiden Schiffe in Seemeilen (nautical miles Nm) nach 5 Stunden. b) Geben Sie für die nebenstehende Situation eine Formel für h an, wenn ϵ, und d gegeben sind. A 4. a) In einem allgemeinen normbeschrifteten Dreieck kennt man die Seiten a = 10 cm, b = 8 cm und die Größe des Winkels = 50°. - Berechnen Sie die Länge der Seite c und die Größe der anderen Winkel. b) Ein Grundstück ist trapezförmig und man kennt man die Länge h = 300 m und b = 500 m und die Winkel ∠ DAB = 90°, ∠ ABC = 90° und ∠ ADC = 109,8°. - Berechnen Sie die Fläche des Grundstücks. 2. Schularbeit aus Mathematik und angewandter Mathematik 2 ak - hall 1. Mittwoch, 22. März 2017 Gruppe B a) Ein Haus mit asymmetrischem Dach (siehe Skizze) hat auf der linken Seite eine Dachneigung von = 40°. –– Das Haus hat eine Breite von AB; = 40 m. –– Die Länge der Dachsparren AC; auf der linken Seite beträgt 15 m. –– - Berechnen Sie die Firsthöhe FC; . –– –– - Berechnen Sie die Entfernungen AF; und FB; und den Winkel . b) Ein Teil einer Schipiste zwischen den Punkten A und B hat eine Hangneigung von = 50°. Die Seehöhe von A beträgt 2 120 m, die von B 1 920 m. –– - Berechnen Sie die Länge der Strecke AB; . Rennfahrerinnen bewegen sich auf diesem Abschnitt mit ca. 108 km/h = 30 m/s. - Berechnen Sie, wie lange sich die Rennläuferin auf diesem Abschnitt befindet. Der Abschnitt nach B verläuft wesentlich flacher und hat eine Hangneigung von 20°. Unter Steigung versteht man das Verhältnis von Höhendifferenz zu waagrechter Entfernung. - Berechnen Sie die Steigung dieses Abschnitts. B 2. a) Ergänzen Sie die folgenden Formeln für die nebenstehende Figur: sin = Error! = cos(90° – ) = b) In einem normal beschrifteten rechtwinkeligen Dreieck kennt man die Fläche A = 26 cm2 und die Länge der Seite a = 4 cm. - Berechnen Sie die beiden nicht rechten Winkel und die Länge der Hypotenuse c B 3. a) Zwei Schiffe fahren gleichzeitig von einem Hafen weg. Schiff A bewegt sich mit der Geschwindigkeit 20 Knoten (kn) (= Seemeilen pro Stunde Nm/h) mit Kurs 60 vom Hafen weg. Schiff B fährt 18 kn mit Kurs 140. - Zeichnen Sie eine Skizze für diese Situation. Die Kursangabe 60 bedeutet, dass der Winkel zur Nordrichtung 60° ist (im Uhrzeigersinn gemessen) - Berechnen Sie die Entfernung der beiden Schiffe in Seemeilen (nautical miles Nm) nach 5 Stunden. b) Geben Sie für die nebenstehende Situation eine Formel für h an, wenn ϵ, und d gegeben sind. B 4. a) In einem allgemeinen normbeschrifteten Dreieck kennt man die Seiten a = 5 cm, b = 4 cm und die Größe des Winkels = 50°. - Berechnen Sie die Länge der Seite c und die Größe der anderen Winkel. b) Ein Grundstück ist trapezförmig und man kennt man die Länge h = 300 m und b = 500 m und die Winkel ∠ DAB = 90°, ∠ ABC = 90° und ∠ ADC = 111,8°. - Berechnen Sie die Fläche des Grundstücks.