Einführung in die Supersymmetrie - Institut für Theoretische Physik
Werbung

Ausarbeitung
Einführung in die Supersymmetrie
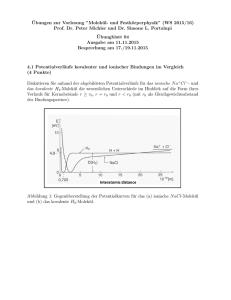
Seminar zur Theorie der Teilchen und Felder
Johannes Michel
Vortrag vom 8. Juli 2015
Betreuer:
PD Dr. Jochen Heitger,
Institut für Theoretische Physik
Inhaltsverzeichnis
Inhaltsverzeichnis
Einführung
2
1 Der
1.1
1.2
1.3
supersymmetrische Oszillator
Erzeuger und Vernichter . . . . . . . . . . . . . . . . . . . . . . . . .
SUSY-Operatoren . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Der SUSY-Oszillator . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
4
5
6
2 Nichtlineare Bose-Fermi-Supersymmetrie
2.1 Superpotential und verallgemeinerter Hamiltonoperator . . . . . . .
2.2 Spektrum und Entartungsgrad . . . . . . . . . . . . . . . . . . . . .
8
8
8
3 Supersymmetrische Quantenmechanik
3.1 Grundlagen . . . . . . . . . . . . .
3.2 Berechnung des Superpotentials . .
3.3 Beispiel Kastenpotential . . . . . .
3.4 SUSY-Ketten und Forminvarianz .
.
.
.
.
11
11
11
12
13
4 Ausblick: SUSY-Feldtheorien
4.1 Graduierte Poincaré-Algebra . . . . . . . . . . . . . . . . . . . . . . .
4.2 Eigenschaften von quantisierten SUSY-Feldtheorien . . . . . . . . . .
15
15
16
Zusammenfassung
18
Literatur
19
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Einführung
Einführung
Supersymmetrie (SUSY) ist ein Konzept, das vielen vage vertraut ist: Der Teilcheninhalt einer supersymmetrischen Theorie umfasst Paare von Bosonen und Fermionen,
die durch eine Symmetrietransformation ineinander überführt werden. Der Spin solcher supersymmetrischer Partner unterscheidet sich dabei um 1/2. Beispielsweise umfassen supersymmetrische Erweiterungen des Standardmodells so genannte Squarks,
Sleptonen oder Gauginos (die supersymmetrischen Partner der Eichbosonen).
(a) Ohne SUSY
(b) Mit SUSY
Abbildung 0: Inverse Kopplungsstärken der elektroschwachen (α2 , α1 ) und starken (α3 )
Wechselwirkung im Rahmen vereinheitlichter SU (5)-Eichtheorien. Entnommen aus [1].
Was aber macht Supersymmetrie als Konzept jenseits des Standardmodells so attraktiv? Prominent werden an dieser Stelle supersymmetrisch erweiterte vereinheitlichte Eichtheorien angeführt (Grand Unified Theories, GUTs). Ohne Supersymmetrie „treffen“ sich die running couplings der Eichwechselwirkungen bei hohen Energien
nicht, was in Abbildung 0a anhand einer GUT mit SU (5) als Eichgruppe nachvollzogen werden kann.1 Das supersymmetrisch erweiterte Modell zeigt dagegen eine
beeindrucke Übereinstimmung der Eichkopplungsstärken bei einer Massenskala von
µ ≈ 1016 GeV (Abbildung 0b): Die Kräfte werden hier nicht nur im Rahmen einer
übergeordneten Eichgruppe vereinheitlicht, sondern auch ganz quantitativ. Als Vorbehalt gilt, dass der markante „Knick“ im Verlauf der running couplings nur dann
eintritt, wenn im Bereich von 102 GeV bis 104 GeV Superpartner von Teilchen des
Standardmodells beobachtet werden [1]. Bekanntlich hat sich dies trotz intensiver
Suche am LHC noch nicht bewahrheitet – die Ausschlussgrenzen für SUSY-Teilchen
1
Im Vortrag wurden die in Abbildung 0 dargestellten Kopplungsstärken fälschlicherweise mit starker, elektromagnetischer und schwacher Wechselwirkung assoziiert. Dies widerspräche dem hier
gezeigten Monotonieverhalten von α2 – bekanntlich ist die Quantenelektrodynamik nicht asymptotisch frei. Vielmehr handelt es sich bei α2 und α1 um die Kopplungskonstanten für die
elektroschwache Eichgruppe SU (2) × U (1) vor spontaner Symmetriebrechung; α3 ist tatsächlich
die Kopplungskonstante der starken Wechselwirkung.
2
Einführung
sind aber im bisherigen Betrieb ebenso wenig erreicht worden. Vielmehr wird die Beobachtung eines Higgs-Bosons bei 125 GeV als Indiz für Supersymmetrie gewertet:
Eine Higgs-Masse unterhalb von ≈ 150 GeV war eine notwendige Bedingung für die
Gültigkeit zumindest der plausibelsten SUSY-Modelle, die typischerweise mehrere,
teils geladene Higgs-Bosonen vorhersagen.
In der vorliegenden Ausarbeitung sollen die Grundlagen supersymmetrischer Theorien auf elementarer Ebene nachvollzogen werden – in je einem einzigen bosonischen und fermionischen Freiheitsgrad. Erstaunlicherweise werden sich die dort erarbeiteten Konzepte als ein wirkungsvolles Werkzeug erweisen, um eindimensionale Quantenmechanik zu betreiben. Trotz der Einschränkung auf elementare SUSYModelle sollen dennoch Bezüge zu SUSY-Feldtheorien hergestellt werden, wo immer
es sich anbietet. Ein Abschnitt zur graduierten Poincaré-Algebra, die Grundlage
von SUSY-Feldtheorien ist, und ein Ausblick auf einige Eigenschaften quantisierter
SUSY-Feldtheorien schließen die Darstellung ab.
3
1 Der supersymmetrische Oszillator
1 Der supersymmetrische Oszillator
1.1 Erzeuger und Vernichter
Als Grundlage der folgenden Überlegungen soll zuerst an den Formalismus von Erzeugern und Vernichtern erinnert werden.2 Vertraut – beispielsweise vom harmonischen
Oszillator – sind die folgenden Kommutatorrelationen für die Operatoren, die ein
Boson erzeugen (b+ ) oder vernichten (b− = (b+ )† ):
[b− , b+ ] = 1
[b− , b− ] = [b+ , b+ ] = 0
(1.1)
Ausgedrückt durch die normierten Eigenzustände |nB i des Teilchenzahloperators
NB := b+ b− gilt
√
√
b− |nB i = nB |nB − 1i , b+ |nB i = nB + 1 |nB + 1i .
Die Bosonenzahl nimmt hier alle Werte nB ∈ N an, der bosonische Fock-Raum hat
abzählbar unendliche Dimension.
Anders liegt der Fall bei Fermionen: Hier postuliert man für den Erzeuger f + und
den Vernichter f − = (f + )† Antikommutator relationen der folgenden Form:
{f − , f + } = 1
{f − , f − } = {f + , f + } = 0
Die zweite Zeile impliziert Nilpotenz der fermionischen Auf- und Absteiger:
2
f+ = f− 2 = 0
(1.2)
(1.3)
Betrachtet man erneut Eigenzustände |nF i von NF := f + f − , gilt
f − |1i = |0i , f + |0i = |1i .
und aus (1.3) folgt, dass |1i durch f + und |0i durch f − annihiliert wird. Der Teilchenzahloperator NF besitzt damit nur die Eigenwerte 0 und 1: Das Pauli-Prinzip
ist gesichert, der fermionische Fock-Raum ist zweidimensional.
Der gesamte Zustandsraum des Systems ist schließlich gegeben durch die direkte
Summe von bosonischem und fermionischem Fock-Raum:
H = span {|nB , nF i} = `2 (N) ⊕ C2
Da b± und f ± auf unterschiedlichen Teilräumen operieren, kommutieren sie offensichtlich miteinander,
[b± , f ± ] = 0 .
(1.4)
2
Der Abschnitt zum supersymmetrischen Oszillator folgt in Notation und Gedankengang Kapitel
2.1 bei Kalka und Soff [2].
4
1.2 SUSY-Operatoren
1.2 SUSY-Operatoren
Gesucht sind nun – gemäß der Grundidee der Supersymmetrie – Operatoren, die
Bosonen und Fermionen ineinander umwandeln:
Q+ |nB , nF i ∝ |nB − 1, nF + 1i
Q− |nB , nF i ∝ |nB + 1, nF − 1i
Diese Anforderung wird erfüllt durch den einfachen Ansatz
Q+ = c · b− f + , Q− = c∗ · b+ f −
mit einem beliebigen Faktor c ∈ C. Die erhaltenen Operatoren Q± sind wegen (1.4)
sogar zueinander adjungiert und nach (1.3) ebenfalls nilpotent,
(Q+ )2 = (Q− )2 = 0 .
(1.5)
Statt Q± können auch hermitesche Linearkombinationen Q1,2 betrachtet werden,
Q1 = Q− + Q+ ,
Q2 = − i(Q− − Q) ,
(1.6)
die Superladungen genannt werden.
Analog zu anderen Symmetrietransformationen soll ein System mit HamiltonOperator HS als supersymmetrisch bezeichnet werden, wenn
[HS , Q± ] = [HS , Q1,2 ] = 0 .
Dies wird bereits durch den einfachen Ansatz
HS = {Q− , Q+ }
(1.7)
erfüllt, denn allein auf Grundlage der Nilpotenz (1.5) gilt
[HS , Q+ ] = Q− Q+ Q+ + Q+ Q− Q+ − Q+ Q− Q+ − Q+ Q+ Q− = 0
und analog für Q− . Mithilfe der Superladungen lässt sich HS kompakt schreiben als
HS = Q21 = Q22 .
Die Superladungen erfüllen außerdem
{Q1 , Q2 } = 0 .
5
(1.8)
1.3 Der SUSY-Oszillator
1.3 Der SUSY-Oszillator
Um die oben beschriebenen Strukturen mit Leben zu füllen, soll der supersymmetrische Oszillator als konkretes Beispiel betrachtet werden. Ausgehend von einem
bosonischen Freiheitsgrad q der Masse m und dem zugehörigen konjugierten Impuls
p in kanonischer Quantisierung
[q̂, p̂] = i ~ ,
[q̂, q̂] = [p̂, p̂] = 0 ,
lassen sich bekanntlich Auf- und Absteigeroperatoren definieren
r
i p̂
mω
±
b =
q̂ ∓
,
2~
mω
die gerade die gewünschten Kommutatorrelationen (1.1) erfüllen. Der HamiltonOperator eines harmonischen Oszillators der Eigenfrequenz ω lässt sich dann umschreiben zu
p̂2
mω 2 2
1
+ −
HB =
+
q̂ = ~ω b b +
2m
2
2
Ähnlich verfährt man für den fermionischen Freiheitsgrad ψ und dessen konjugierten Impuls π. Hier fordert man in kanonischer Quantisierung
{ψ̂, π̂} = 0 ,
{ψ̂, ψ̂} = {π̂, π̂} = ~ .
Auch hier werden die fundamentalen Relationen (1.2) durch geeignete Linearkombinationen erfüllt,
r 1
f± =
ψ̂ ∓ i π̂ .
2~
Der so genannte Fermi-Oszillator lässt sich wieder ausdrücken durch Auf- und Absteiger:
1
+ −
HF = i ω ψ̂π̂ = ~ω f f −
2
Der Hamilton-Operator des Gesamtsystems ist dann
HB + HF = ~ω(b+ b− + f + f − )
Bemerkenswerterweise gilt mit der Wahl c =
metrischen Hamilton-Operator aus (1.7)
√
~ω für den einfachsten supersym-
HS = {Q− , Q+ }
= c∗ c {b+ f − , b− f + }
= ~ω b+ b− f − f + + b− b+ f + f −
= ~ω b+ b− 1 − f + f − + 1 + b+ b− f + f −
= ~ω b+ b− + f − f +
6
(1.9)
1.3 Der SUSY-Oszillator
unter Ausnutzung der fundamentalen Relationen (1.1) und (1.2). Dieses Ergebnis
stimmt mit (1.9) exakt überein: Wenn – wie hier – gleiche Eigenfrequenzen ωF = ωB
angenommen werden, ist der „SUSY-Oszillator“ (1.9) inhärent supersymmetrisch.
Zum Spektrum von HS lassen sich zwei Bemerkungen treffen, die über das einfache
Beispielsystem hinausweisen: Erstens beobachtet man, dass das Vakuum |Ωi = |0, 0i
Eigenzustand von HS zur Energie E = 0 ist, die Nullpunktsenergie hΩ|H|Ωi = 0 verschwindet also. Dies ist erfreulich im Hinblick auf freie Felder in kanonischer Quantisierung, die sich als Modenentwicklung von Oszillatoren schreiben lassen: Dort war
(etwa beim freien Skalarfeld
oder beim Maxwell-Feld in Strahlungseichung) eine DiR 3
vergenz hΩ|H|Ωi ∝ d p ω(p)/2 nur durch Normalordnung des Hamilton-Operators
gezielt zu vermeiden. In einer Modenentwicklung aus SUSY-Oszillatoren tritt eine
derartige Divergenz nicht auf, der Vakuumerwartungswert der Energie verschwindet. Zweitens lässt sich zum Spektrum von HS bemerken, dass – mit Ausnahme des
Grundzustandes – alle Energien E = ~ω(nB +nF ) genau zweifach entartet sind. Dies
ist eine Eigenschaft, die im Folgenden auch weitere supersymmetrische Systeme aufweisen werden. Das Spektrum von HS ist in Abbildung 1.1 dargestellt, einschließlich
der Wirkung der SUSY-Operatoren Q± auf die gemeinsamen Eigenzustände von HS
und NF = f + f − .
Q+
3
2
2
1
Q−
1
0 = nB
nB = 0
E=0
nF = 0
nF = 1
Abbildung 1.1: Spektrum des SUSY-Oszillators (1.9) und Wirkung der SUSY-Operatoren
Q± . Nach einer Darstellung in [2].
7
2 Nichtlineare Bose-Fermi-Supersymmetrie
2 Nichtlineare Bose-Fermi-Supersymmetrie
2.1 Superpotential und verallgemeinerter Hamiltonoperator
Wie oben bemerkt, folgt Supersymmetrie von HS = {Q− , Q+ } direkt aus (Q± )2 =
0.3 Ein allgemeinerer Ansatz für Q± lautet daher
Q+ = B − f + , Q − = B + f − .
Die Operatoren B ± haben die Gestalt
i p̂
1
B = √ W (q̂) ∓ √
m
2
±
(2.1)
mit einer beliebigen analytischen Funktion W des Ortsoperators, dem so genannten
Superpotential. Aus den kanonischen Relationen für q̂, p̂ ergeben sich für B ± verallgemeinerte (Anti-)Kommutatorrelationen:
{B − , B + } = W 2 +
p̂2
,
m
1
~ dW
[B − , B + ] = √ [i p̂, W (q̂)] = √
m
m dx
(2.2)
Für den allgemeinen Hamilton-Operator B − B + f + f − + B + B − f − f + ist eine Matrixschreibweise üblich,
+ −
H1 0
B B
0
=:
.
HS =
0 H2
0
B−B+
Der obere (untere) Diagonaleintrag bezieht sich hier auf den Eigenraum von NF zum
Eigenwert 0 (1). Offensichtlich lassen sich H1,2 mit (2.2) auch schreiben als
1
p̂2
1
~ dW
1
H1,2 = {B − , B + } ∓ [B − , B + ] =
+ W2 ∓ √
.
2
2
2m 2
2 m dx
(2.3)
Ein lineares Superpotential W (q̂) ∝ q̂ reproduziert – wie wir öfter bemerken werden
– den SUSY-Oszillator.
2.2 Spektrum und Entartungsgrad
Das Spektrum des allgemeinen supersymmetrischen Hamilton-Operators (2.1) teilt
einige Charakteristika des SUSY-Oszillators. Um diese zu zeigen ist es nützlich, erneut Q1,2 wie in (1.6) zu definieren.
3
Dieser Abschnitt beruht auf Kapitel 2.3 bei Kalka und Soff [2].
8
2.2 Spektrum und Entartungsgrad
1. Alle Eigenwerte von HS sind nichtnegativ.
Beweis. Klar, da HS = Q21 das Quadrat eines hermiteschen Operators ist.
2. Jeder Eigenwert E > 0 ist zweifach entartet.
Beweis.√Sei |Ai Eigenzustand von H zum Eigenwert E und von Q1 zum Eigenwert + E. Da [Q1 , Q2 ] 6= 0, ist |Bi := Q2 |Ai linear unabhängig. Außerdem
gilt wegen (1.8)
√
√
Q1 |Bi = Q1 Q2 |Ai = −Q2 Q1 |Ai = − EQ2 |Ai = − E |Bi ,
und |Bi ist ebenfalls Eigenzustand von H zum Eigenwert E.
3. Falls ein Grundzustand E = 0 existiert, ist er nicht entartet: Höchstens einer
der Operatoren H1 = B + B − und H2 = B − B + besitzt Eigenwert 0.
(1,2)
Beweis. Angenommen es existieren Grundzustände |ψ0
B + B − und H2 = B − B + Es gilt
(1)
(1)
i jeweils von H1 =
(1)
(2)
H1 |ψ0 i = 0 ⇒ B − |ψ0 i und H2 |ψ0 i = 0 ⇒ B + |ψ0 i .
(1)
(1)
(1)
(Betrachte die Norm hψ0 |H1 |ψ0 i = |B − |ψ0 i |2 , analog für H2 .) Der Annihilation durch B ± entspricht in Ortsdarstellung die Differentialgleichung
~ d
(1,2)
√
± W ψ0 (x) = 0 .
m dx
Diese hat formal die Lösungen
(1,2)
ψ0 (x)
√ Z x
m
dy W (y) .
= C exp ∓
~ 0
Allerdings ist höchstens eine der Lösungen normierbar – abhängig vom asymptotischen Verhalten des Integrals im Exponenten: Notwendige Bedingung für
einen normierbaren Grundzustand von H1 zum Eigenwert E = 0 ist
Z 0
Z ∞
dy W (y) = −∞ und
dy W (y) = +∞ .
−∞
0
Notwendige Bedingung für einen Eigenwert E = 0 von H2 sind dagegen gerade
die umgekehrten Vorzeichen; die Bedingungen schließen sich also aus. Andere
Vorzeichenkombinationen sind hinreichend dafür, dass kein Zustand bei E = 0
existiert. Die unterschiedlichen Fälle sind in Abbildung 2.1 in Abhängigkeit
vom Verlauf des Superpotential dargestellt.
Aus den oben getroffenen Aussagen ergeben sich drei mögliche Szenarien für das
Spektrum von HS (Abbildung 2.2): Entweder besitzt H1 einen Eigenwert E = 0
9
2.2 Spektrum und Entartungsgrad
Abbildung 2.1: Ein Grundzustand bei E = 0 liegt je nach den asymptotischen Vorzeichen
des Superpotentials vor. Entnommen aus [2].
oder H2 oder keiner der beiden Operatoren. In den ersten beiden Fällen wird die
Supersymmetrie als „exakt“ bezeichnet, im letzten als „gebrochen“. Die zuerst nicht
ganz intuitiven Bezeichnungen erschließen
P sich, wenn man die Supersymmetrie zu
einer kontinuierlichen Symmetrie exp(i k ak Qk ), ak ∈ R „befördert“. Eine exakte
Symmetrie liegt dann vor, wenn der Zustand minimaler Energie |Ωi invariant ist:
!
X
exp i
ak Qk |Ωi = |Ωi
k
Ableiten nach den Parametern ak liefert Qk |Ωi = 0: Die Symmetrie ist also exakt,
wenn der Grundzustand durch die Superladungen annihiliert wird. Dies ist in den
grün und rot unterlegten Fällen in Abbildung 2.2 gegeben, da der Grundzustand
keinen Superpartner besitzt. Im blau unterlegten Fall gehen die beiden Zustände
minimaler Energie dagegen durch Q1,2 ineinander über und die kontinuierliche Symmetrie ist spontan gebrochen.
SUSY exakt
gebrochen
E=0
Abbildung 2.2: Mögliche Szenarien für das Spektrum des Gesamtsystems HS (schematisch): Entweder besitzt H1 (grün) oder H2 (rot) einen Eigenwert E = 0 oder keiner der
beiden Operatoren (blau). Alle Eigenwerte E > 0 sind entartet. Nach Kalka und Soff [2].
10
3 Supersymmetrische Quantenmechanik
3 Supersymmetrische Quantenmechanik
3.1 Grundlagen
Der im letzten Abschnitt eingeführte Formalismus der nichtlinearen Supersymmetrie
kann umgedeutet werden: Statt als Hamilton-Operatoren auf Teilräumen zu nF = 0
und nF = 1 können H1,2 als eigenständige eindimensionale quantenmechanische Systeme angesehen werden4 . Alle Resultate für die Spektren und Eigenzustände können
dann übertragen werden – vorausgesetzt, die Faktorisierung
H1 = B + B − , H2 = B − B +
in verallgemeinerte Auf- und Absteiger bleibt erhalten. Dies ist nach (2.3) erfüllt,
wenn ein Superpotential W existiert mit
~2 d2
~ dW
1
2
H1,2 = −
W ∓√
.
(3.1)
+ V1,2 (x) , V1,2 =
2m dx2
2
m dx
Nehmen wir exakte Supersymmetrie an: H1 sei ohne Beschränkung der Allgemeinheit
(1)
(1)
der Hamilton-Operator mit Eigenwert E0 = 0. Abgesehen von E0 sind die beiden
Spektren dann identisch,
(1)
(1)
E0 = 0 , En(2) = En+1 .
(3.2)
Auch Eigenzustände werden einfach durch B ± in ihren „Superpartner“ übersetzt:
1
(1)
ψn(2) = q
B − ψn+1
(1)
En+1
(3.3)
Hier bietet sich eine weitere Interpretation von B ± an. Bekanntlich gilt bei eindimensionalen Potentialen, dass der Index n bei aufsteigender Ordnung E0 < E1 < · · · <
En < . . . der Zahl der Knoten der Wellenfunktion ψn (x) entspricht [3, S. 256 f.]:
B − vernichtet und B + erzeugt einen Knoten. Mithilfe von (3.2) und (3.3) können
über elementare Rechnungen völlig neue quantenmechanische Potentiale erschlossen
werden; bei gebrochener SUSY treten in allen Ausdrücken gleiche Indices n auf.
3.2 Berechnung des Superpotentials
Um die Möglichkeiten des SUSY-Formalismus in quantenmechanischen Anwendungen auszuschöpfen, fehlt noch eine konstruktive Vorschrift, aus einem gegebenen
Potential V1 das Superpotential W und damit das Partnerpotential V2 zu gewinnen. Vorausgesetzt werden muss exakte Supersymmetrie: H1 habe den (bekannten)
(1)
Grundzustand ψ0 =: ψ0 zum Eigenwert E = 0. Der verblüffend einfache Ausdruck
für das Superpotential ist dann
~ d
W = −√
ln ψ0 .
m dx
4
Der folgende Abschnitt fußt auf Kapitel 3.1 bei [2].
11
(3.4)
3.3 Beispiel Kastenpotential
Beweis. Die Eigenwertgleichung H1 ψ0 = 0 lässt sich mit (3.1) ausschreiben als
~
~2 00 1
2
0
W − √ W ψ0 = 0 .
−
ψ +
2m 0 2
m
Da ψ0 keine Knoten besitzt, gilt äquivalent
ψ000
=
ψ0
√
m
W
~
√
2
m
W
~
−
0
.
Durch Vergleich mit der Quotientenregel
ψ000
=
ψ0
ψ00
ψ0
0
+
ψ00
ψ0
2
liest man (3.4) als eine Lösung ab.
Das Vorgehen beim Auffinden des Partnerpotentials V2 ist zusammenfassend in
Abbildung 3.1 dargestellt: Nach Lösen der Eigenwertgleichung von H1 zum Eigenwert E = 0 kann das Superpotential mit (3.4) sofort angegeben werden. Geeignete
Linearkombinationen von W 2 und W 0 führen dann zurück auf V1 oder eben zu V2 .
Das einfachste Beispiel ist erneut der harmonische Oszillator V1 ∝ x2 . Bekanntlich
ist ψ0 (x) dann eine Gauß-Funktion: Deren logarithmische Ableitung ist aber – wie
zu erwarten war – ein lineares Superpotential W ∝ x. Das Partnerpotential V2 ist
dann erneut das Potential eines harmonischen Oszillators, gegenüber V1 lediglich
verschoben um einen konstanten Offset 2W 0 .
1
2
2 (W
1
2
2 (W
− W 0)
W
V1
d
− dx
ln ψ0
H1 ψ0 = 0
+ W 0)
V2
ψ0
Abbildung 3.1: Vorgehen beim Auffinden des Partnerpotentials V2 . Nach [2].
3.3 Beispiel Kastenpotential
Als ein letztes Beispiel soll das Partnerpotential des unendlich tiefen Kastens der
Länge L = 1 angegeben werden. Der Einfachheit halber sind für diesen Abschnitt
12
3.4 SUSY-Ketten und Forminvarianz
auch ~ = m = 1 gesetzt.5 Die bekannten Energien und der Grundzustand des eindimensionalen Kastens sind
√
1
En = (n + 1)2 , ψ0 (x) = 2 sin(πx) .
(3.5)
2
Über (3.4) und (3.1) folgt
π2
2
W = −π cot(πx) , V2 =
−1 .
2 sin2 (πx)
Das Spektrum dieses – zugegeben ungewöhnlichen – Potentials ist damit sofort durch
den einfachen Ausdruck (3.5) gegeben. Die Spektren und niedrigsten angeregten
Zustände der beiden Potentiale sind in Abbildung 3.2 vergleichend dargestellt.
Abbildung 3.2: Das Kastenpotential (links) und sein Partnerpotential (rechts) im Vergleich. In breitem Strich sind die Potentiale eingezeichnet; Haarlinien entsprechen den
Energieniveaus und den zugehörigen Zuständen. Entnommen aus Kalka und Soff [2].
3.4 SUSY-Ketten und Forminvarianz
Beim Konzept des einfachen Partnerpotentials muss man nun keineswegs Halt ma(2)
chen: Vielmehr kann V2 nach Umdefinition des Energienullpunktes E0 := 0 als
das Ausgangspotential für das in Abbildung 3.1 gezeigte Verfahren gewählt werden.
Iterativ ergibt sich dann eine so genannte SUSY-Kette – auch wenn das Verfahren
sich hier weit vom ursprünglichen konzeptionellen Rahmen einer Symmetrie zwischen
Bosonen und Fermionen entfernt hat. Nützlich ist das Verfahren aus zwei Gründen:
Einerseits kann durch wiederholte Anwendung von Bi− aus den angeregten Zuständen
von V1 der Grundzustand jedes Potentials in der Kette ermittelt werden. Falls andererseits die angeregten Zustände unbekannt und die Grundzustände der einzelnen
Potentiale gegeben sind, lässt sich das Verfahren auch umkehren.
Eine wichtige Aussage über SUSY-Ketten bleibt hier notgedrungen Randnotiz: Es
lässt sich zeigen, dass die unter SUSY-Partnerbildung forminvarianten Potentiale
5
Detailliert und mit allen Parametern findet sich die Rechnung in Abschnitt 3.1.4 bei [2].
13
3.4 SUSY-Ketten und Forminvarianz
gerade die algebraisch lösbaren Potentiale sind. Als Beispiel dient – wieder einmal
– der harmonische Oszillator: In diesem Fall sind alle Potentiale in der Kette harmonische Oszillatoren. Angeregte Zustände gehen durch wiederholte Anwendung des
Aufsteigers Bi+ = b+ aus dem Grundzustand hervor, was in Ortsdarstellung auf die
bekannten Hermite-Polynomen führt.
B1−
3
2
1
0
B1+
(1)
B2−
2
1
0
B2+
(2)
B3−
2
1
B4−
0
B3+
(3)
B4+
(4)
Abbildung 3.3: Aufbau einer SUSY-Kette (schematisch), nach [2].
14
4 Ausblick: SUSY-Feldtheorien
4 Ausblick: SUSY-Feldtheorien
4.1 Graduierte Poincaré-Algebra
Teilchen sind in „gewöhnlichen“ Feldtheorien irreduzible Darstellungen der PoincaréGruppe. Die Lie-Algebra der Poincaré-Gruppe supersymmetrisch zu erweitern stellt
daher ein natürliches Verfahren dar, den Teilcheninhalt der Theorie zu vergrößern.
Bereits in den Überlegungen zum SUSY-Oszillator wurde allerdings klar, dass Superladungen Antikommutator relationen genügen und damit den Rahmen einer LieAlgebra sprengen. Der erweiterte mathematische Rahmen, in dem Supersymmetrie
fassbar wird, ist die so genannte Graduierung, die zuerst eingeführt werden soll.6
Anschließend werden die Neuerungen der graduierten Poincaré-Algebra vorgestellt
und mit den bisherigen Resultaten in einer (Raum-)Zeitdimension verglichen.7
Eine Z2 -graduierte Lie-Algebra L = L0 ⊕ L1 mit Produkt ◦ erfüllt mit xi ∈ Li die
folgenden Eigenschaften:
Graduierung
xi ◦ xj ∈ L(i+j mod 2) ,
(4.1)
Supersymmetrie
xi ◦ xj = −(−1)i·j xj ◦ xi
(4.2)
und eine verallgemeinerte Jacobi-Relation
xk ◦ (xl ◦ xm )(−1)k·m + xl ◦ (xm ◦ xk )(−1)l·k + xm ◦ (xk ◦ xl )(−1)m·l = 0 .
(4.3)
Eine Lie-Algebra im ursprünglichen Sinne ist hier nur L0 : Für i = j = k = m =
0 reduziert sich (4.2) auf die Forderung nach Antisymmetrie des Produkts ◦, das
dann der Kommutator ist. Auch die Jacobi-Relation (4.3) reduziert sich innerhalb
von L0 auf die übliche definierende Eigenschaft von Lie-Algebren. Dagegen ist L1
für sich betrachtet nicht einmal eine Algebra: An (4.1) liest man leicht ab, dass
das Produkt von zwei Elementen aus L1 wieder in L0 liegt.8 Entscheidend ist, dass
das Produkt seinen Charakter wechselt: Innerhalb von L0 und zwischen L0 und L1
ist es nach (4.2) der Kommutator. Zwischen Elementen von L1 wirkt es dagegen
wir der Antikommutator. Dies ist gerade die Eigenschaft, die für eine geschlossene
Behandlung von Superladungen erforderlich ist.
Spezifizieren wir nun L0 3 P µ , M µν als die Poincaré-Algebra mit den Komponen-
6
Die Darstellung nimmt hier Bezug auf Kapitel 9.1 in [2].
Kapitel 9.3 in [2]
8
K-Graduierung mit einem größeren endlichen Körper K setzt genau an dieser Stelle an: Statt
nach zwei „Schritten“ wie hier für Z2 „kehrt“ das Produkt erst nach mehreren Verknüpfungen
„zurück“ in den Ausgangsraum.
7
15
4.2 Eigenschaften von quantisierten SUSY-Feldtheorien
ten P µ des Viererimpulses als Generatoren der Translation und
0
K1 K2 K3
−K1
0
J3 −J2
M µν =
−K2 −J3
0
J1
−K3 +J2 −J1
0
als eine kompakte Notation für die Generatoren von Boosts (Ki ) und Rotationen
(Ji ).9 Diese Algebra wird graduiert durch Hinzufügen der Komponenten Qa ∈ L1
einer Majorana-wertigen Superladung.10 Um die Algebra im Sinne von (4.1) und
(4.2) zu schließen, müssen zusätzlich folgende (Anti-)Kommutatorrelationen gelten:
[M µν , Qa ] = −Σµν
ab Qb ,
[P µ , Qa ] = 0 ,
µ
{Qa , Q̄b } = 2γab
Pµ
Hier bietet sich ein Vergleich an mit den Beziehungen (1.2) und (1.8), die für einen
einzigen Feld-Freiheitsgrad (also in einer eindimensionalen Raumzeit) gefunden wurden:
[HS , Qj ] = 0
{Qj , Qk } = 2HS δjk , j, k = 1, 2
Tatsächlich ergibt sich mit HS = P0 als dem einzigen verbleibenden Generator von
Translationen eine enge Übereinstimmung, da alle Spinor-Strukturen ohne Raumdimensionen entfallen.
4.2 Eigenschaften von quantisierten SUSY-Feldtheorien
Abschließend sollen einige bemerkenswerte Eigenschaften von quantisierten SUSYFeldtheorien zusammengetragen werden – die meisten natürlich ohne Beweis:11
• Ist die Supersymmetrie bezüglich des Vakuums Ω exakt, gilt
hΩ|H|Ωi = 0 .
Beweis. Exakte Supersymmetrie bedeutet erneut, dass das Vakuum durch die
Superladungen annihiliert wird, Qa |Ωi = Q̄b |Ωi = 0. Wegen Translationsinvarianz gilt in jedem Fall P |Ωi = 0 für den Dreierimpuls. Bilden des Erwarµ
tungswertes hΩ| . . . |Ωi auf beiden Seiten von {Qa , Q̄b } = 2γab
Pµ liefert dann
die Behauptung.
• In SUSY-Eichtheorien mit N = 4 Majorana-Superladungen auf einer vierdimensionalen Raumzeit verschwindet die Symanzik-β-Funktion in allen Ordnungen Störungstheorie, β(g) = 0 („no renormalization theorem“).
9
Die Kommutatorrelationen für P µ , M µν finden sich etwa als Gleichung 7.134 in [2].
Effektiv sind damit von den vier Spinor-Komponenten von Q nur zwei festzulegen.
11
Auswahl und Darstellung der Eigenschaften folgen [4].
10
16
4.2 Eigenschaften von quantisierten SUSY-Feldtheorien
• Etwas schwächere Resultate über „günstiges“ Verhalten der β-Funktion gewinnt
man auch für andere Anzahlen N von Superladungen.
Auf phänomenologischer Seite darf natürlich nicht unerwähnt bleiben, dass SUSYPartner bei gleichen Massen durch das Experiment ausgeschlossen sind. Falls also
Supersymmetrie in der Natur realisiert ist, ist sie durch spontane Symmetriebrechung
„verborgen“ – zumindest auf den zugänglichen Energieskalen.
17
Zusammenfassung
Zusammenfassung
• Supersymmetrie bildet fermionische und bosonische Zustände aufeinander ab.
• Die Summe aus fermionischem und bosonischem Oszillator ist das einfachste
Beispiel für ein supersymmetrisches System.
• Nichtlineare Supersymmetrie kann auch für allgemeinere Systeme gelten. Der
Entartungsgrad des Grundzustands hängt hier nur von topologischen Eigenschaften des Superpotentials ab.
• Die SUSY-Faktorisierung ist ein mächtiges Werkzeug zum Lösen quantenmechanischer Probleme. Der Supersymmetrie-Charakter des Problems geht dabei
ein wenig verloren.
• SUSY-Feldtheorien „erben“ einige Eigenschaften der einfachen Modelle in einem Freiheitsgrad. Beispielsweise verschwindet der Vakuumerwartungswert der
Energie.
18
Literatur
Literatur
[1]
G. G. Ross. „Evidence of supersymmetry“. Nature 352 (6330 1991), S. 21–22.
[2]
H. Kalka und G. Soff. Supersymmetrie. Teubner-Studienbücher Physik. Stuttgart 1997.
[3]
W. Nolting. Quantenmechanik - Grundlagen. Bd. 5/1. Grundkurs Theoretische
Physik. Berlin 2013.
[4]
M. E. Peskin und D. V. Schroeder. An introduction to quantum field theory.
Reading, Mass. 1995.
Abbildungsverzeichnis
0
Kopplungsstärken in vereinheitlichten Eichtheorien. . . . . . . . . . .
2
1.1
Spektrum des SUSY-Oszillators . . . . . . . . . . . . . . . . . . . . .
7
2.1
2.2
Fallunterscheidung für das Superpotential. . . . . . . . . . . . . . . .
Szenarien für Spektren supersymmetrischer Systeme. . . . . . . . . .
10
10
3.1
3.2
3.3
Vorgehen beim Auffinden des Partnerpotentials. . . . . . . . . . . . .
Das Kastenpotential und sein Partnerpotential. . . . . . . . . . . . .
Aufbau einer SUSY-Kette. . . . . . . . . . . . . . . . . . . . . . . . .
12
13
14
19