Kurze Einführung in SPSS 11.5

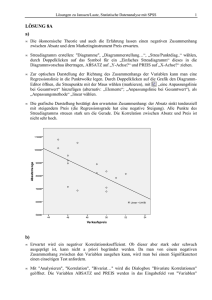
 Matthias Gabriel
Kurze Einführung in SPSS 11.5
2001
überarbeitet Oktober 2003
1
 Matthias Gabriel
Legende: Im folgenden Text entsprechen die Wörter zwischen Anführungszeichen den
Befehlen bzw. Menüoptionen im SPSS
z.B: „Berechnen“, „Zählen“, „Umkodieren“...
1 Datenaufbereitung
1.1 Die SPSS-Matrix
Der SPSS Editor ist in eine Datenansicht und eine Variablenansicht geteilt (links unten am
Bildschirm). Zwischen den beiden Ansichten kann beliebig gewechselt werden.
1) Die Datenansicht zeigt die vom Benutzer eingegeben Daten an, wobei die Personen
(Fälle) senkrecht angereiht sind und die Variablen waagrecht.
Jede Person i hat also eine ganze Zeile Zi in der ihre Ausprägungen in allen Variablen
k sichtbar werden.
Jede Variable j hat eine Spalte Sj in der die Ausprägungen aller Personen n in dieser
Variable sichtbar werden.
2) Die Variablenansicht gibt Auskunft über die Definitionen und Merkmale der
einzelnen Variablen Vj, wobei in dieser Ansicht die Variablen senkrecht aufgereiht
sind (jede Zeile = eine Variable) und jedes Merkmal, jede Einstellung dieser Variable
eine Spalte darstellt.
Folgende Einstellungen (jede Spalte ist eine Einstellung) werden angeboten:
a) Name: hier wird der Variablenname eingegeben (max. 8 Zeichen, der Name
muss mit einem Buchstaben beginnen), der in der Datenansicht dann über der
Spalte erscheint und somit die „Überschrift“ der Variable darstellt.
b) Typ: Numerisch (für Zahlen), Währung (für Geld), Datum, String (für
Zeichen, Buchstabenketten, alphanumerische Kombination)...
c) Spaltenformat (benutzerdefiniert je nach Variable)
d) Dezimalstellen
e) Variablenlabel: Der hier eingeschriebene Name der Variable wird beim
Output automatisch verwendet; z.B. bei Tabellen, Diagrammen, Tests...(der
Name aus Punkt a) wird also nicht(!) beim Output verwendet)
f) Wertelabels: Hier kann man Werte einer Variablen definieren (meist bei
nominalskalierten bzw qualitiativen Variablen). z.B: Wert „0“ für „männlich“,
Wert „1“ für „weiblich“ (bei Geschlecht), oder „16-20“ für „jung“ und „21-25“
für „mittel“... (bei Altersklassen).
Erscheint ebenfalls im Output (wie das Variablenlabel).
g) Fehlende Wert: Definition des „missing-Wertes“: Falls Personen in
verschiedenen Zellen, Variablen keine Werte haben, wird diese Zelle nicht
einfach ausgelassen! Der missing-Wert wird eingegeben. (z.B: „-1“ oder „99“ ,
damit er nicht mit anderen Werten leicht vertauscht werden kann). Diese
Eingabe ist ebenfalls wichtig für die Auswertung.
h) Spalten: für Spaltenbreite (benutzerdefiniert je nach Variable)
i) Ausrichtung: wo die Werte in der Zelle angeordnet sein sollen (rechts, links...)
j) Messniveau: Nominal (z.B: Geschlecht, Bildung, Hobby...) Ordinal (=
Rangskala z.B: Noten, Dienstgrad...) Metrisch (= Verhältnisskala z.B: Größe,
Gewicht, Längen und u.a. auch Rohwerte...)
4
 Matthias Gabriel
1.2 Variablen definieren
Definition: Die oben genannten Einstellungen (a bis j) für eine Variable modifizieren. Dies
geschieht in der Regel gleich zu Beginn der Dateneingabe.
Beispiel: Variable „Geschlecht“ defineren
a) Name: „Gender“
b) Typ: „numerisch“
c) Spaltenformat: 8
d) Dezimalstellen: 0
e) Variablenlabel: Geschlecht
f) Wertelabels: Wert „0“ hat Wertelabel „männlich“ und Wert „1“ hat Wertelabel
„weiblich“ („hinzufügen“ nicht vergessen!)
g) fehlende Wert „-1“
h) Spalten: 8
i) Ausrichtung: rechts
j) Messniveau: „nominal“
1.3 Variablen verschieben, einfügen
Verschieben: Variable markieren (beim Variablennamen), mit linker Maustaste nochmals
anklicken, Taste halten und dann weiterschieben. Erst wenn richtige Stelle erreicht ist,
Mausknopf loslassen. (eine andere Möglichkeit besteht mit kopieren und einfügen)
Einfügen: In der Datenansicht Variable rechts neben der neu einzufügenden Variable
markieren (beim Variablennamen), dann rechter Mausklick und „Variable einfügen“.
1.4 Fälle (Personen) einfügen
In der Datenansicht die Zeile unter der neu einzufügenden Zeile markieren (bei Fallnummer),
dann rechter Mausklick und „Fälle einfügen“.
1.5 Fälle, Variablen löschen
Zeile bzw. Spalte markieren (wie unter 1.3 bzw. 1.4) und „entfernen“ drücken.
1.6 Daten sortieren (sort)
Definition: Sortiert alle Fälle nach einer bestimmten Variable auf- oder absteigend.
Beispiel: Alle Personen nach Alter aufsteigend sortieren (also vom Jüngsten zum Ältesten)
„Daten“ → „Fälle sortieren“ → In „sortieren nach“ die gewünschte Variable eingeben nach
der sortiert werden soll (hier Alter) → „aufsteigend“ → „ok“
5
 Matthias Gabriel
1.7 Dateien aufteilen (split)
Definition: Um den Datensatz (imaginär) in Untergruppen zu teilen, z.B: Frauen und Männer
trennen, nach Altersklassen aufteilen...
Anwendung: z.B. bei der Normalverteilungsprüfung, bei Diagrammen, Tabellen und anderen
deskriptiven Auswertungen
Beispiel: Die Daten bezüglich Geschlecht aufteilen
„Daten“ → „Datei aufteilen“ → „Ausgabe nach Gruppen aufteilen“ anklicken und die
gewünschte split-Variable eingeben (hier Geschlecht) → „ok“
Die Daten werden jetzt für alle Berechnungen immer als gesplittet angesehen,
dementsprechend gibt es auch im Output immer getrennte Ergebnisse.
Nicht vergessen die Aufteilung wieder aufzuheben, falls sie nicht mehr gebraucht wird.
1.8
Fälle auswählen bzw. filtern (select)
Definition: Um nur bestimmte Fälle in die Berechnungen einzubeziehen
1) Fälle nach bestimmten Kriterien auswählen
Beispiel: Es werden nur jene Fälle für die Auswertung benötigt, die älter als 35 Jahre sind.
„Daten“ → „Fälle auswählen“ → „Falls Bedingung zutrifft“ anklicken → „Falls“ →
Bedingungsvariable hinzufügen (hier Alter) und Bedingung festlegen (hier „>35“
dazuschreiben) →“weiter“ → „ok“
2) Zufallsstichprobe
Definition: um aus den Daten eine repräsentative Stichprobe auszuwählen (meist nur für
große Datensätze)
„Daten“ → „Fälle auswählen“ → „Zufallsstichprobe“ anklicken
3) Aufgrund einer Filtervariablen filtern
Beispiel: Daten nach Geschlecht filtern
„Daten“ → „Fälle auswählen“ → „Filtervariable verwenden“ anklicken → gewünschte
Filtervariable hinzufügen (hier Geschlecht) → „nicht ausgewählte Fälle“: „löschen“ oder
(besser) „filtern“ auswählen
Die Daten werden jetzt für alle Berechnungen immer als gefiltert angesehen, daher nicht
vergessen die Filterung wieder aufzuheben, falls sie nicht mehr gebraucht wird.
1.9
Variablen kategorisieren
Definition: Kategorisiert eine gewünschte Variable in k (selbst wählbare) Klassen. Die Wahl
der Klassengrößen erfolgt automatisch!
6
 Matthias Gabriel
Anmerkung: Falls die Klassengrößen selbst definiert werden wollen (besser): siehe unter
1.11 Variablen umkodieren
Beispiel: Das Alter soll in 4 Klassen eingeteilt werden
„Transformieren“ → „Variablen kategorisieren“ → In „Kategorien erstellen für“ gewünschte
Variable hinzufügen (hier Alter) → die „Anzahl der Kategorien“ festlegen (hier 4) → „ok“
Ergebnis: Eine neue Variable (hier nalter) mit 4 Kategorien wird erzeugt.
1.10
Zählen...
Definition: Zählt zeilenweise bestimmte Werte nach benutzerdefiniert aufgestellten Formeln.
Das Ergebnis wird in einer neuen Variablen angegeben.
Dieser Befehl kann sehr hilfreich sein, etwa bei der Frage: „Wie oft hat eine Person bei
bestimmten Items/Variablen bestimmte Werte gewählt?“ oder „Wie oft hat eine Person bei
den 20 Items die Antwortmöglichkeit A gewählt?“
Anwendungsbeispiele:
• Darstellung des Antwortverhaltens der einzelnen Personen
• Häufigkeiten von Werten in Zeilen (also pro Person) zählen
Beispiel: Ein Persönlichkeitsfragebogen mit 10 Fragen, 5 kategorielles Antwortmuster. Wie
oft hat eine Versuchsperson Antwort 1, 2, 3, 4, bzw. 5 angekreuzt?
„Transformieren“ → „Zählen...“ → In „Zielvariable“ den Namen der neuen Variable
eingeben (z.B: „Antw_1“ für Antwortmöglichkeit 1) → In „Label“ den Variablennamen
eingeben (zB: „Häufigkeit Antwort 1“) (siehe auch 1.1) → In „Variablen“ jene Variablen
eingeben, die für den Zählvorgang berücksichtigt werden sollen (hier: Item1 bis Item 10) →
„Werte definieren“ → unter „Wert“ den gewünschten zu zählenden Wert eingeben (hier: „1“)
→ „hinzufügen“ → „weiter“ → „ok“
Ergebnis: Eine neue Variable (hier: „Antw_1“) wird erzeugt in der die Häufigkeiten der
Antwortalternative „1“ in den 10 Items für jede Person dargestellt wird.
→ analog erfolgt die Darstellung der anderen 4 Antwortmöglichkeiten in 4 neuen Variablen.
Im Alert-Fenster „Werte definieren“ besteht auch die Möglichkeit nicht nur konkrete einzelne
Werte, sondern auch Wertbereiche und missing Werte, die zu zählen sind, anzugeben.
1.11
Variablen umkodieren (recode)
Ein sehr wichtiger Befehl.
Anwendungsbeispiele:
• Das Alter in einer neuen Variable in Altersklassen einteilen,
• Die Kodierung einzelner Items umdrehen (bei Rating- Likertskalen), also z.B: die
Werte 1,2,3,4,5 in 5,4,3,2,1 umdrehen.
7
 Matthias Gabriel
•
Bestehende Kodierungen umändern: zB: 4 Schulformkategorien (AHS, HTL, HBLA,
HAK) in 2 umkodieren (AHS und „Andere“), sodass unter „Andere“ HTL, HBLA
und HAK enthalten sind.
Die Umkodierung wird in derselben Variablen durchgeführt, oder (besser) es wird eine neue
Variable mit der neuen Kodierung erzeugt.
Beispiel 1: Das Alter (stetige Variable) in die Altersklassen (qualitativ dreikategorielle
Variable) „15-30“, „31-39“ und „40+“ umkodieren. Dafür soll eine neue Variable erzeugt
werden.
„Transformieren“ → „Umkodieren“ →
„in andere Variablen“
→ gewünschte
umzukodierende Variable hinzufügen (hier Alter) → in „Ausgabevariable“ „Name“ den
Namen der neuen Variablen eingeben (z.B: alter2) und „ändern“(!) drücken → „Label“
einschreiben (z.B: „Alter dreikategoriell“) (siehe auch 1.1) → „alte und neue Werte“ → „alter
Wert“ „Bereich“ anklicken (weil ein Altersbereich angegeben werden muss) → die ersten
Klassengrenzen eingeben (hier: 15 und 30) → unter „neuer Wert“ neuen „Wert“ angeben
(hier: „1“ für 1.Altersklasse) → „hinzufügen“ → analog den zweiten Bereich (31 bis 39)
eingeben und 2 für 2. Altersklasse als neuen Wert → für die letzte (offene!!) Klasse (40+)
„Bereich“ „kleinster Wert bis“ anklicken und „40“ eingeben → als „neuen Wert“ „3“ (für 3.
Klasse) „hinzufügen“ → „weiter“ → „ok“
Ergebnis: am Ende der Datenmatrix in der Datenansicht wird nun die neue Variable
(„alter2“) hinzugefügt, welche die Variable Alter in 3 Klassen einteilt. („1“ für 15-13, „2“ für
31-39 und „3“ für 40 und älter)
Die neue Variable muss noch definiert werden (siehe 1.1)
Beispiel 2: Die Werte des 5 kategoriellen Items 1 sollen umkodiert werden, in einer anderen
Variable; also 5 zu 1, 4 zu 2, 3 zu 3, 2 zu 4 und 1 zu 5.
„Transformieren“ → „Umkodieren“ →
„in andere Variablen“
→ gewünschte
umzukodierende Variable hinzufügen (hier Item1) → in „Ausgabevariable“ „Name“ den
Namen der neuen Variablen eingeben (z.B: Item1_a) und „ändern“(!) drücken → „Label“
einschreiben (z.B: „Item1 umkodiert“) → „alte und neue Werte“ → „alter Wert“ „1“ eingeben
→ „neuer Wert“ „5“ eingeben → “hinzufügen“ → analog für die anderen 4 Werte (2 zu 4; 3
zu 3; 4 zu 2 und 5 zu 1) → „weiter“ → ok“
Ergebnis: am Ende der Datenmatrix wird nun die neue Variable („Item1_a“) mit den
umkodierten Werten hinzugefügt.
Die neue Variable muss noch definiert werden (siehe 1.1)
Automatisch umkodieren
Das obige Beispiel 2 kann auch einfacher gelöst werden mit „automatisch umkodieren“
Fortsetzung Beispiel 2:
„Transformieren“ → „automatisch umkodieren“ → gewünschte umzukodierende Variable
hinzufügen (hier Item1) → in „Neuer Name“ den Namen der neuen Variablen eingeben (z.B:
„Item1_a“) und „Neuer Name“(!) drücken → „Umkodieren beginnen bei „größtem Wert“
wählen → „ok“
Ergebnis: Am Ende der Datenmatrix wird nun die neue Variable („Item1_a“) hinzugefügt
Die neue Variable muss noch definiert werden (siehe 1.1)
8
 Matthias Gabriel
1.12
Der Befehl „Berechnen“ (compute)
Der „Berechnen“-Befehl ist ebenfalls eine sehr hilfreiche Anwendung.
Definition: (zumeist zeilenweise) Berechnung von bestimmten statistischen Kennwerten,
Formeln, deren Ergebnis in einer neuen Variable aufscheint.
Anwendungsbeispiele:
• Welchen Rohscore haben die Personen in den k Items (Variablen) (also eine
zeilenweise Summierung der Werte der k Items für jede Person, in einer neuen
Variablen ausgegeben)
• Welchen Mittelwert, welche Varianz, Standardabweichung... hat jeder Fall in den k
Variablen
• Viele weitere Berechnungen (z.B: Body-Maß-Index, relative Lösungshäufigkeiten,
Summen, Wurzel, Potenzen, Logarithmen, Median, Modalwert...)
Beispiel 1: Welche relative Lösungshäufigkeit weist jede Peson in den 10 Items auf?
„Transformieren“ → „Berechnen“ → In „Zielvariable“ gewünschten Namen der neuen
Variable einschreiben (z.B. relHfgkt) → im Feld „numerischer Ausdruck“ werden alle
gewünschten Berechnungen eingetragen. Dafür muss man einfach die benötigten Variablen
aus der Variablenliste einfügen und mit den erwünschten Rechenoperatoren verknüpfen.
Dieses Beispiel verlangt die Anzahl der gelösten Items (Variable „rohscore“) dividiert durch
die Anzahl aller n Items für jede Zeile:
Man schreibt bzw. fügt ins Berechnungsfeld also folgendes ein:
“rohscore / 10”
→ „ok“
Ergebnis: Eine neue Variable „relHfgkt“ wird nun erzeugt, die für jede Person die relative
Lösungswahrscheinlichkeit angibt.
Berechnen mittels Funktionen
Verschiedene vorprogrammierte Berechnungen (wie Mittelwert, Median, Varianz,
Standardabweichung...) sind den vorprogrammierten Funktionen zu entnehmen. Diese
vereinfachen den Rechenprozess oft wesentlich.
Beispiel 2: Mittelwertsberechnung mittels vorprogrammierter Funktion
Die Funktionen sind im Feld „Funktionen“ ersichtlich und mit englischen Wörtern abgekürzt.
Für eine Direkthilfe braucht man nur die gewünschte Funktion markieren und die rechte
Maustaste klicken.
Für unser Beispiel wäre es die Funktion unter „M“ wie „Mean“ (Mittelwert) also
„Mean(numausdr, numausdr,...)“
Die gewünschten 10 Items müssen noch eingefügt und mit einem Beistrich getrennt(!)
werden. Dies sieht so aus:
“MEAN(item1,item2,item3,item4,item5,item6,item7,item8item9,item10)”
→ „ok“
Dies wäre die Berechnung des Mittelwertes mittels Funktion.
Ergebnis: Eine neue Variable wird nun erzeugt, die für jeden Fall den Mittelwert der Werte
der 10 Items angibt.
9
 Matthias Gabriel
2 Deskriptive Statistik
2.1 Tabellen
2.1.1 einfache Tabellen
Definition: zur einfachen, übersichtlichen Darstellung bzw. Zusammenfassung der Werte
(Häufigkeiten) von Variablen nach ihren Ausprägungen (z.B.: Ja/Nein; Geschlecht; Alter...)
Befehl: „Analysieren“ → „Tabellen“ → „einfache Tabellen“ → gewünschte Variable(n) in
„Zeilen“ oder/und „Spalten“ geben → „ok“
Beispiel:
Zeilen: Semester in denen sich die Vps befinden (1-9)
Spalten: Unterteilung Geschlecht (dichotom)
aktuelles Semester 1
2
3
4
5
6
7
9
Geschlecht
männlich
42
12
6
4
1
2
weiblich
237
33
55
7
11
2
1
1
Variationen:
• separate Tabellen (z.B.: je eine Tabelle für Männer/Frauen): → gewünschte Variable
(z.B.: Geschlecht) in „separate Tabellen“ geben um 2 separate Tabellen für 1) Männer
2) Frauen zu erhalten
• gestapelte/verschachtelte Tabellen
• Zeilen/Spaltenprozente, Prozentangaben...: → „Statistik“
• die Anordnung der Zeilen/Spaltenprozente, Prozentangaben...innerhalb der Tabelle
können geändert werden:
→ „Layout“ → „Beschriftung für Statistik“ wie gewünscht ändern
• Werte sortieren: → „Statistik“
• Gesamtwerte (Gesamtergebnis für die Tabelle / Zeilen/Spaltensummen): → „Gesamt“
• Darstellung leerer Zellen (z.B.: mit Null): → „Format“
2.1.2 Häufigkeitstabellen
Definition: Häufigkeitstabellen sind den einfachen Tabellen sehr ähnlich. Sie eignen sich aber
zusätzlich besonders zur Darstellung von Häufigkeiten mehrerer Variablen, welche gleiche
Antwortmöglichkeiten/kategorien haben (z.B.: Ja/Nein/weiß nicht; Multiple Choice...)
Beispiel:
Spalten: Zufriedenheit und Lebenssituation (2 Variablen(!))
Zeilen: Antwortkategorien (bei beiden Variablen gleich(!))
Befehl: „Analysieren“ → „Tabellen“ → „Häufigkeitstabellen“
10
 Matthias Gabriel
Allgemeine Zufriedenheit
Anzahl
Sehr zufrieden
467
Ziemlich zufrieden 872
Nicht sehr zufrieden 165
Ist das Leben aufregend oder langweilig?
Anzahl
434
505
41
Variation:
• Für jede Variable eine eigene Spalte: → alle gewünschten Variablen in „Häufigkeit
für“ geben
• Verschachtelte Tabellen (mehrdimensional): → zusätzliche Variable(n) in „In jeder
Tabelle“ geben
• Separate verschachtelte Tabellen: → zusätzliche Variable(n) in „separate Tabellen“
geben
• Prozente, Gesamtwerte: → „Statistik“
2.1.3 allgemeine Tabellen
Definition: Mit allgemeinen Tabellen können Mehrfachantworten ausgewertet werden
(mehrdimensionale Darstellungen, also viele Variablen in einer Tabelle). Weiters können
auch verschiedene Stufen der Verschachtelung innerhalb der Tabellen festgelegt werden.
Befehl: „Analysieren“ → „Tabellen“ → „allgemeine Tabellen“
Beispiel 1: (eine verschachtelte mehrdimensionale Tabelle)
In den Zeilen: Beschreibung der Lebenssituation und (verschachteltes) Geschlecht
In der Spalte: die Region (Lebensraum)
Ist das Leben aufregend oder Aufregend Männlich
langweilig?
Weiblich
Routine
Männlich
Weiblich
Langweilig Männlich
Weiblich
Region
Nordost
92
94
88
140
7
12
Südost
56
51
58
90
3
9
West
65
76
54
75
2
8
Beispiel 2: (eine unverschachtelte mehrdimensionale Tabelle)
In den Zeilen: Beschreibung der Lebenssituation und (unverschachteltes) Geschlecht
In der Spalte: die Region
Region
Nordost
Ist das Leben aufregend oder langweilig? Aufregend 186
Routine
228
Langweilig 19
Geschlecht
Männlich 281
Weiblich 398
11
Südost
107
148
12
177
238
West
141
129
10
178
245
 Matthias Gabriel
Variationen:
• Verschachteln von einzelnen Variablen (z.B.: Geschlecht): → Variable markieren und
„Verschachtelt“ wählen
• Zellenstatistiken für einzelne Variablen (z.B.: nur Geschlecht hat Zeilenprozente alle
anderen haben Absolutwerte): → Variable markieren und „Statistik bearbeiten“
wählen
• Gesamtwerte einblenden: → Variable markieren und „Gesamtergebnis einfügen“
wählen.
• Mittelwert, Varianz.... berechnen: → Variable markieren und „wird ausgewertet“
wählen: → dann „Statistik“ wählen und die gewünschten Statistiken (Mittelwert...)
„hinzufügen“ (eventuell Mittelwert... markieren und „Format“ ändern für
Dezimalzahlen)
12
 Matthias Gabriel
2.2 statistische Kennwerte (deskriptive Statistiken)
2.2.1 Mittelwert, Varianz, Median, Standardabweichung...+ Diagramme
1. Möglichkeit: (mit Diagrammen)
Befehl: „Analysieren“ → „deskriptive Statistiken“ → „Häufigkeiten“ → gewünschte Variable
eingeben (z.B. Alter) → „Statistik“ → gewünschte Statistiken eingeben (z.B.7 Mittelwert,
Varianz...)
→ „Diagramme“ → gewünschtes Diagramm eingeben
Beispiel:
Anzahl der Geschwister
N
Gültig
Fehlend
Mittelwert
Median
Standardabweichung
Varianz
1505
12
3,93
3,00
3,05
9,28
2. Möglichkeit: (leichter und übersichtlicher Vergleich von Mittelwerten, Varianzen...
bezüglich Kategorien) ohne Diagramme
Beispiel: Welchen Mittelwert, welche Varianz... hat die Variable Alter separat dargestellt
nach der Variable Geschlecht?
Befehl: „Analysieren“ → „Mittelwerte vergleichen“ → “Mittelwerte...“ → in „unabgängige
Variable“ kommt die Breakvariable (hier: Geschlecht) → in „abhängige Variable“ kommt
jene Variable, deren Statistiken (Mittelwert...) ausgerechnet werden soll (hier Alter) →
„Optionen“ → gewünschte statistische Kennwerte hinzufügen → „weiter“ → „ok“
Bericht
alter
Geschlecht
männlich
weiblich
Insgesamt
Mittelwert
24,15
21,65
22,04
Standardabweichung
6,14
3,97
4,46
Varianz
37,757
15,743
19,928
Median
22,00
20,00
21,00
3. Möglichkeit: (über Tabellen)
Befehl: „Analysieren“ → „Tabellen“ → „einfache Tabellen“ → die gewünschte Variable(n)
in das Feld „Auswerten“ geben → „Statistik“ → die gewünschten statistischen Kennwerte
(zB: Mittelwert, Median, Varianz..) „hinzufügen“ (eventuell das „Format“ „ändern“, um
Dezimalzahlen anzuzeigen).
Beispiel:
Mittelwert Median Standardabweichung Varianz
Anzahl Geschwister 3,932
3,000 3,047
9,282
13
 Matthias Gabriel
4. Möglichkeit: (eher für Intervallskalierte Daten, ohne Median, Modalwert...)
Befehl: „Analysieren“ → „deskriptive Statistiken“ → „deskriptive Statistiken...“ →
Variable(n) eingeben → „Optionen“ → gewünschte Statistiken auswählen
Beispiel:
N
Mittelwert Standardabweichung Varianz
Anzahl Geschwister
1505 3,93
3,05
9,282
Gültige Werte (Listenweise) 1505
2.3 Diagramme
Definitionen:
• Balkendiagramm: gibt pro Balken die Werte einer Ausprägung (z.B.: Mann/Frau)
einer Variable (z.B.: Geschlecht) an.
• Kreisdiagramm: ein „Kuchen“ dessen „Kuchenstücke“ die verschiedenen
Ausprägungen darstellen (z.B.: Anzahl der Studiensemester). Desto mehr Personen in
eine Kategorie fallen (z.B.: erstes Semester) desto größer ist dieses Kuchenstück.
• Histogramm: (Vergleich: Häufigkeitsklassen) Verwendung: bei stetigen(!) Variablen,
wenn die Variable in Klassen gegliedert ist oder in Klassen abgebildet werden soll
(z.B.: Körpergröße, Klassen: 151-160cm, 161-170cm,...)
• Streudiagramm: (XY-Diagramm) Jeder Punkt im Diagramm hat einen X und einen Y
Koordinate. Dadurch ergibt sich eine Punktwolke. Verwendung: z.B.: Regression,
Korrelation, Modellkontrolle Rasch Modell
• Liniendiagramm: gibt eine Gerade/Kurve/Funktion an. Verwendung z.B.: bei
Einkommen, Alter, Körpergröße, Konzentrationskoeffizienten...
Befehl: → „Grafiken“ → gewünschten Diagrammtyp (Balken, Kreis...) auswählen
Beispiel 1: Balkendiagramm
Wie viele Kinder haben männliche bzw. weibliche befragte Personen im Durchschnitt?
Lösung: Darstellung mittels Balkendiagramm mit a) Kategorienvariable: Geschlecht b)
auszuwertende Variable: durchschnittliche Anzahl der Kinder (Mittelwert)
Befehl: → „Grafiken“ → „Balken...“ → „einfach“ und „Auswertung über Kategorien einer
Variable“ (weil hier nur Kategorien der einen Variable Geschlecht gefragt sind. Für die
Abbildung mehrerer Variablen in einem Diagramm → „Auswertung über verschiedene
Variablen“ wählen) → „definieren“ → in „Kategorienachse“ Geschlecht hinzufügen → bei
„Bedeutung der Balken“ „andere Auswertefunktion“ wählen (weil der Mittelwert der Anzahl
der Kinder gefragt ist und nicht die Häufigkeit bzw. Anzahl der Fälle) → gewünschte
auszuwertende Variable hinzufügen (hier Anzahl der Kinder) → „Auswertefunktion“ →
„Mittelwert“ wählen → „weiter“ → „ok“
14
 Matthias Gabriel
Ergebnis:
2,2
2,1
2,0
Mittelwert Anzahl Kinder
1,9
1,8
1,7
1,6
1,5
Männlich
Weiblich
Geschlecht
Die durchschnittliche Anzahl der Kinder überwiegt bei den Frauen (ca. 2,1) im Vergleich zu
den Männern (ca 1,6).
Variationen:
• Häufigkeiten oder Prozente der Ausprägungen einer Variablen angeben (z.B.: Wie
viele Männer/Frauen) → „Anzahl der Fälle“ oder „%der Fälle“ wählen statt „andere
Auswertefunktion“
• Fehlende Werte anzeigen (als eigenen Balken) → „Optionen“
• Diagrammtitel → „Titel“
• Varianz, Median, Standardabweichung... → „andere Auswertefunktion“ (wie bei
Mittelwert)
Anmerkung: Die Darstellung von Kreis-, Linien-, Flächendiagramm erfolgt fast äquivalent.
Beispiel 2: Histogramm
Nur sinnvoll bei (quantitativen) Variablen, die eine Klassenbildung benötigen, um
zusammengefasst zu werden (z.B: Alter, Körpergröße, Gewicht, (Punkte in einem Test)...)
Nicht bei qualitativen Variablen!
Frage: Wie sieht die Verteilung der Variable „Alter“ aus?
Eine Abbildung des Alters mit jedem Alter (Jahr) als eigene Kategorie bei einer Stichprobe
von z.B:15 bis 70 jährigen wäre nicht sinnvoll und überhaupt nicht überschaubar.
Lösung: Altersklassen bilden und Histogramm erstellen
Befehl: → „Grafiken“ → „Histogramm“ → in „Variable“ die gewünschte Variable
einfügen (hier: Alter) → „ok“
300
200
100
Std.abw. = 4,45
Mittel = 22,0
N = 419,00
0
20,0
25,0
22,5
30,0
27,5
35,0
32,5
40,0
37,5
45,0
42,5
47,5
alter
Die Verteilung des Alters in diesem Beispiel ist nicht normalverteilt, die Klasse 19-21jährige
beinhaltet den Großteil der Stichprobe.
Variationen:
• „Normalverteilungskurve (dazu) anzeigen“
Anmerkung: Die Klassen werden in der Regel automatisch gebildet.
15