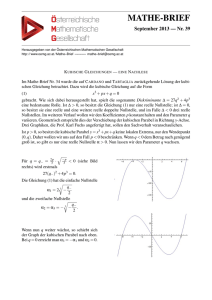
Lineare Algebra I a) A = b) A = c) A = 0 −i T(x) = n ≥ 0.

Institut für Mathematik
Karl-Franzens-Universität Graz
Clason, Fripertinger, Kainrath
Blatt 11
UE 621.011
WS 2008/09
Lineare Algebra I
Hausaufgaben (Bearbeitung bis 14.1.2009)
H 11.1 Nullstellen reeller Polynome ungeraden Grades
(a) Zeigen Sie, dass jedes normierte reelle Polynom vom Grad 3 mindestens eine reelle Nullstelle besitzt.
(b) Verallgemeinern Sie diesen Beweis und zeigen Sie, dass jedes reelle Polynom von ungeradem Grad mindestens eine reelle Nullstelle besitzt.
H 11.2 Invariante Unterräume
Bestimmen Sie alle A-invarianten Unterräume des R2 für
µ
¶
µ
¶
2 0
0 1
a) A =
,
b) A =
,
0 2
1 0
µ
c) A =
¶
2 1
.
4 2
H 11.3 Einsetzen von Matrizen in Polynome
µ
(a) Seien p =
X2
+ 1 ∈ P (C) und A =
¶
i 0
. Berechnen Sie p( A).
0 −i
(b) Seien p ∈ P (K), A, B ∈ Kn×n und B sei invertierbar. Zeigen Sie p( BAB−1 ) = Bp( A) B−1 .
(c) Sei wieder p = X 2 + 1. Zeigen Sie, dass es unendlich viele Matrizen A ∈ C2×2 mit
p( A) = 0 gibt.
H 11.4 Charakterisierung von Eigenwerten
Sei T : Kn → Kn eine lineare Abbildung und A die Abbildungsmatrix von T bezüglich der
Standardbasis des Kn (also T ( x ) = Ax für alle x ∈ Kn ). Zeigen Sie, dass für λ ∈ K äquivalent
sind:
(a) λ ist ein Eigenwert von T.
(b) Die Matrix A − λE (E = n × n-Einheitsmatrix) hat einen Rang < n.
Sind diese Bedingungen erfüllt, so ist ker( A − λE) der zu λ gehörende Eigenraum von T.
H 11.5 Berechnung von Eigenwerten
Berechnen Sie die Eigenwerte und zugehörigen Eigenräume der linearen Abbildung T : R3 →
R3 mit


0
1
0
0
1 x
T ( x ) = 0
6 −11 6
für alle x ∈ R3 .
Freiwillige Trainingsbeispiele (werden von Tutoren korrigiert)
T 11.1 Gradformeln
Beweisen Sie die Gradformeln für Polynome f und g:
Grad( f + g) ≤ max{Grad( f ), Grad( g)}.
Grad( f g) = Grad( f ) + Grad( g).
Wir verwenden dabei die Konvention n + (−∞) = (−∞) + n = (−∞) + (−∞) = −∞ und
n > −∞ für alle ganzen Zahlen n ≥ 0.