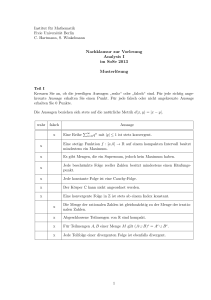
A 17 Bestimmen Sie jeweils den Grenzwert der Folge an,n ∈ N, für

WS 15/16 Vorlesung/Übung
Mathematik 1 : Thema 4.1 - Aufgaben
A 17
Bestimmen Sie jeweils den Grenzwert der Folge an , n ∈ N, für n → ∞
n3 − 2n2 + 5
a) an =
4n3 − 7n
5n4/5 − n3/4
b) an = 5/6
3n + 2n2/3
1/2
c) an = (n2 − 1)
−n+1
A 18
Bestimmen Sie für die Folge sn , n ∈ N, mit sn =
a) den endlichen Summenwert
n
�
i=0
(a − 1)i , wobei a > 0 fix
b) den Grenzwert für n → ∞
A 19
Bestimmen Sie jeweils für die Folge sn , n ∈ N, den Grenzwert für n → ∞
n
n 4i+2 − 32i−1
�
�
k+2
2k−1
4 /3
b) sn =
a) sn =
17i
i=0
k=3
�
c) sn = nk=0 54 ( 56 )k − 65 ( 45 )k
A 20
Eine endliche Folge von jährlichen Zahlungen ai (i = 1, . . . , n), die um den
konstanten Betrag |d| abnehmen , soll sich in n Jahren zu einem Wert von
sn = 60 aufsummieren (z.B. bei einer einfachen Form der Abschreibung oder
der Mittelbewirtschaftung).
Die Zahlungen erfolgen in festgelegten, nicht weiter teilbaren Geldeinheiten/Stückelungseinheiten.
Hierbei sind zunächst nur positive Zahlungen ai zugelassen.
a) Welchen Wert hat d und wie errechnet sich sn aus d, n und dem Anfangswert a1 ?
b) n = 5 Jahre und |d| = 4 werden festgelegt. Welchen Wert muß a1 haben?
c) a1 = 15 und |d| = 2 werden festgelegt. Was folgt für die Anzahl n?
d) n = 10 Jahre und a1 = 24 werden festgelegt.
Ist damit das Ziel sn = 60 realisierbar?
Falls ja, mit welchem Wert von |d|?
e) Wie oben (a)–(d), wenn nun auch Zahlungen ai ≤ 0 zugelassen sind.
Mathematik für Ökonomen - Campus Duisburg
1 von 2
WS 15/16 Tutorien
Mathematik 1 : Thema 4.1 - Aufgaben
T 17
Bestimmen Sie jeweils den Grenzwert der Folge an , n ∈ N, für n → ∞
√
√
n3 − 2n2 + 5
2
√
a) an =
b)
a
=
=
n
+
2
−
n
c)
a
√
n
n
4n3 − 7n
n+2+ n
n3/4 − 2n5/4 + 5n−1/2 − 7n3/2
d) an =
4n3/2 − 7n−1 + n4/3
e) an = nk /nm (k, m ∈ Q fest)
Wählen Sie jeweils ganze Zahlen k und m so, dass
e1)
lim nk = 0 und lim nm = ∞ und lim nk · nm = 0
n→∞
e2)
e3)
n→∞
n→∞
lim nk = 0 und lim nm = ∞ und lim nk · nm = 1
n→∞
n→∞
n→∞
lim nk = 0 und lim nm = ∞ und lim nk · nm = ∞
n→∞
n→∞
n→∞
T 18
Bestimmen Sie für die Folge sn , n ∈ N, mit sn =
a) den endlichen Summenwert
b) den Grenzwert für n → ∞
n
�
i=0
√ i
(1 − 1/ 2)
T 19
Bestimmen Sie jeweils für die Folge sn , n ∈ N, den Grenzwert für n → ∞
�
a) sn = nk=1 3k+2 /22k
�
b) sn = nk=0 3( 32 )k − 2( 34 )k
T 20
Eine endliche Folge von jährlichen Zahlungen ai (i = 1, . . . , n), die um den
konstanten Betrag |d| zunehmen , soll sich in n Jahren zu einem Wert von
sn = 420 aufsummieren (z.B. bei einer einfachen Form der Abschreibung
oder der Mittelbewirtschaftung). Die Zahlungen erfolgen in festgelegten, nicht
weiter teilbaren Geldeinheiten/Stückelungseinheiten.
a) Welchen Wert hat d und wie errechnet sich sn aus d, n und dem Anfangswert a1 ?
b) n = 5 Jahre und |d| = 28 werden festgelegt. Welchen Wert muß a1 haben?
c) a1 = 42 und |d| = 21 werden festgelegt. Was folgt für die Anzahl n?
d) n = 15 Jahre und a1 = 7 werden festgelegt. Ist damit das Ziel sn = 420
realisierbar? Falls ja, mit welchem Wert von |d|?
Mathematik für Ökonomen - Campus Duisburg
2 von 2