Teil IV: Komplexe Zahlen

Brückenkurs Mathematik
Geschichte
Teil IV: Komplexe Zahlen
ì
820 erstmals Problem der Wurzel aus
negativen Zahlen belegt:
x 2Ÿ4xŸ5 0
x 1, 2 ‚2&Ɓ 4‚5
x 1, 2 ‚2&Ɓ ‚1
ì
1554 Cardano: „Wenn man mit Wurzeln aus
negativen Zahlen rechnen könnte, so wären
viele Probleme lösbar
17. Jahrhundert:
A& Ɓ ‚B ' imaginäre Zahl'
Staatliche Studienakademie Leipzig
Studienrichtung Informatik
Prof. Dr. Ingolf Brunner
15. September 2011
ì
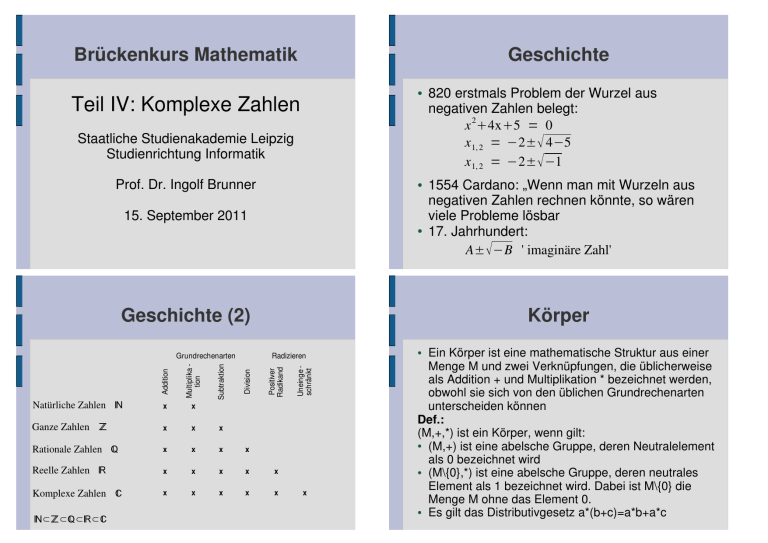
Geschichte (2)
Ganze Zahlen ^
x
x
x
Rationale Zahlen Z
x
x
x
x
Reelle Zahlen \
x
x
x
x
x
Komplexe Zahlen Q
x
x
x
x
x
X¥^¥Z¥\¥Q
Uneinge schränkt
x
Positiver
Radikand
x
Division
Natürliche Zahlen X
Subtraktion
Multiplika tion
Radizieren
Addition
Grundrechenarten
Körper
x
Ein Körper ist eine mathematische Struktur aus einer
Menge M und zwei Verknüpfungen, die üblicherweise
als Addition + und Multiplikation * bezeichnet werden,
obwohl sie sich von den üblichen Grundrechenarten
unterscheiden können
Def.:
(M,+,*) ist ein Körper, wenn gilt:
ì (M,+) ist eine abelsche Gruppe, deren Neutralelement
als 0 bezeichnet wird
ì (M\{0},*) ist eine abelsche Gruppe, deren neutrales
Element als 1 bezeichnet wird. Dabei ist M\{0} die
Menge M ohne das Element 0.
ì Es gilt das Distributivgesetz a*(b+c)=a*b+a*c
ì
Definition
ì
Komplexe Zahlen erweitern den Körper der reellen Zahlen derart,
dass sämtliche (nicht konstanten) algebraischen Gleichungen
auflösbar werden, z. B. nicht nur
x ‚10
(Reelle Lösungen +1 und -1)
sondern auch
(Keine reelen Lösungen)
x 2 Ÿ10
Eigenschaften
ì
ì
Die erste Komponente des Paares (a,b), also a, nennt man den
Realteil der komplexen Zahl (a, b), den zweiten, also b, den
Imaginärteil.
ì
Komplexe Zahlen mit Imaginärteil 0 verhalten sich wie reelle
Zahlen:
2
Definition:
Eine komplexe Zahl ist ein Paar (a,b) zweier reeller Zahlen a und b.
Für die Addition gilt: (a, b) + (c, d) = (a + c, b + d)
(d.h. komponentenweise).
Für die Multiplikation gilt (a, b)·(c, d) = (a·c - b·d, a·d + b·c).
Die Menge Q der Paare reeller Zahlen mit den so definierten
Verknüpfungen bildet einen Körper ( Q , +, * ) .
ì
Ǝa ,0ƏŸƎc , 0Ə ƎaŸc , 0Ə
Ǝa ,0Ə·Ǝc ,0Ə Ǝa·c , 0Ə
ì
Imaginäre Einheit
ì
Die Zahl (0, 1) bekommt folgende Eigenschaft:
2
Ǝ0,1Ə Ǝ0,1Ə·Ǝ0,1ƏƎ‚1, 0Ə‚1
ì
Damit sind x=(0, 1) und x=(0, -1) Lösungen der
Gleichung x 2Ÿ10
ì
Die komplexe Zahl (0, 1) nennt man die imaginäre
Einheit, kurz i (oder auch j in der Elektrotechnik).
Komplexe Zahlen lassen sich also in Realteil und
Imaginärteil zerlegen:
Ǝa , bƏƎa ,0ƏŸƎ0, bƏƎa ,0ƏŸƎb , 0Ə·Ǝ0,1ƏaŸb·i
ì
Konjugiert komplexe Zahl Z*:
*
Z Ǝa , bƏaŸb·i
Z Ǝa ,‚bƏa‚b·i
Jede reele Zahl ist eine komplexe Zahl mit dem Imaginärteil Null
“Klammerrechnung”
ì
Damit kann von der Paarschreibweise zu einer "gewohnten"
Schreibweise übergegangen werden, wobei man neben den
reellen Zahlen a, b jetzt aber eine weitere Zahl i benutzt, die die
Eigenschaft i 2 = -1 besitzt, und die daher auch als "Wurzel aus -1"
aufgefasst wird.
ì
Addition und Multiplikation lassen sich damit als übliche
Klammerrechnung interpretieren:
Ǝa ,bƏŸƎc , d ƏƎaŸbiƏŸƎcŸdiƏƎaŸcƏŸƎbŸd ƏiƎaŸc ,bŸd Ə
Ǝa ,bƏ·Ǝc , d ƏƎaŸbiƏ·ƎcŸdiƏacŸadiŸbciŸbdi 2
ac‚bd ŸƎad ŸbcƏiƎac‚bd , ad ŸbcƏ
ì
Komplexe Zahlen sind im Gegensatz zu reellen Zahlen nicht mehr
geordnet, d.h. es gibt keine Relation “<” oder “>” zwischen ihnen.
Komplexe Ebene
Während sich die Menge \ der reellen Zahl an einer Zahlengeraden veranschaulichen lässt, kann man die Menge Q der
komplexen Zahlen als Ebene (komplexe Ebene, Gauss'sche
Ebene) interpretieren. Die Menge der reellen Zahlen bildet darin
die waagerechte Achse, die Menge der rein imaginären Zahlen
(d.h. mit Realteil 0) bildet die senkrechte Achse.
ì
Polardarstellung
ì
Anstatt durch seine Koordinaten a und b kann ein Punkt in der
Ebene auch durch den Abstand vom Ursprung (0,0) und den
Winkel zwischen der waagerechten Achse und der Verbindung
zum Ursprung beschrieben werden (Polarkoordinaten).
rƁ a 2 Ÿb 2
Ƹarctan
ƎƏ
b
a
sowie
ar·cos Ƹ
br·sin Ƹ
Man nennt r den Betrag und
Ƹ das Argument der Zahl z .
Darstellung
ì
Eulersche Identität
ei Ƹ cos ƸŸi sin Ƹ
Daraus folgt die Darstellung:
zƎa ,bƏaŸbir Ǝcos ƸŸi sin ƸƏr·E ƎƸƏ
ì
Hierbei ist E ƎƸƏeine komplexe Zahl vom Betrag 1
und vom Argument Ƹ .
„Wenn man sich umdreht, schaut man in die
andere Richtung.“ Zusammenhang von e, i und π:
ei ƳŸ1 0
ì
Herleitung der Eulerschen Identität:
Sie kann auch wie folgt interpretiert werden:
E ƎƸƏe
f ƎƸƏ iƸ
Damit ergibt sich:
zƎa ,bƏaŸbir Ǝcos ƸŸi sin ƸƏr·E ƎƸƏr·ei Ƹ
Nenner ist nie Null:
1. Ableitung:
Untersuchen f(0):
cos ƸŸi sin Ƹ
ei Ƹ
e ·e
e 1
f ' ƎƸƏ 0
n
cos 0Ÿi sin 0
f Ǝ0Ə 1 n
ei 0
iƸ
‚i Ƹ
0
f ƎƸƏ const.
f ƎƸƏ 1
Interpretation der Multiplikation
ì
ì
Dies ermöglicht auch eine geometrische Interpretation der
Multiplikation. Mit:
Interpretation der Division
ì
Dies ermöglicht auch eine geometrische Interpretation der
Division. Mit:
Ǝa ,bƏr·E ƎƸƏr·ei Ƹ
Ǝc , d Əs·E ƎƺƏs·ei ƺ
Ǝa ,bƏr·E ƎƸƏr·ei Ƹ
Ǝc , d Əs·E ƎƺƏs·ei ƺ
wird
wird
Ǝa ,bƏ·Ǝc , d Ər·ei Ƹ·s·ei ƺ
r·s·e iƎƸŸƺƏr·s·E ƎƸŸƺƏ
Ǝa , bƏ
r·ei Ƹ
r
r
·ei ƎƸ‚ƺƏ ·E ƎƸ‚ƺƏ
iƺ
Ǝc , d Ə
s
s
s·e
D.h. die Beträge werden multipliziert und die Argumente
(Winkel) addiert.
ì
D.h. die Beträge werden dividiert und die Argumente
(Winkel) subtrahiert.
Wurzel
Logarithmus
ln Z ln ƎaŸi bƏ ln Ǝr·ei ƸŸi k 2Ƴ Ə
1
ƁZ Z n
n
n{\
iƸ
r e r Ǝcos ƸŸi sin ƸƏ
i ƸŸi k 2 Ƴ
r ƎcosƎƸŸk 2 ƳƏŸi sin ƎƸŸk 2 ƳƏƏ r e
Rechenregeln für Logarithmen:
ln Ǝ x·yƏ ln xŸln y
ln Ǝr·e i ƸŸi k 2Ƴ Ə ln r Ÿ ln Ǝe i ƸŸi k 2 Ƴ Ə
ln r Ÿ i ƎƸŸk 2ƳƏ
Damit folgt:
ƁZ Z
n
1
n
Ǝr e
1
iƸŸi k 2 Ƴ n
Ə
1
rn e
Kreis mit Radius Ɓ r
n Lösungen: k 0,1, 2,... ,Ǝn‚1Ə
(Prinzip Rechenschieber!)
i ƸŸi k 2Ƴ
n
Lösungen:
ln Z ln rŸi ƎƸŸk 2ƳƏ
n
Hauptwert:
‚Ƴ Ź ƎƸŸk 2ƳƏ ¡ Ƴ
(Einschränkung auf einen Streifen der komplexen Zahlenebene)