Preisbildung bei Marktmacht: Preisdiskriminierung im Monopol

Preisbildung bei Marktmacht:
Preisdiskriminierung im Monopol
Universität Erfurt
Wintersemester 08/09
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
1 / 35
Einführung
Ohne Marktmacht (bei vollkommenem Wettbewerb) wird die
Preisbildung durch Marktangebot und -nachfrage bestimmt.
Der einzelne Produzent muss in der Lage sein, den Markt
vorherzusehen, und sich dann darauf konzentrieren, die
Produktion (Kosten) so zu gestalten, dass die Gewinne
maximiert werden.
Bei der Preisbildung mit Marktmacht (bei nicht vollkommenem
Wettbewerb) muss der einzelne Produzent neben seiner Aufgabe
bei der Gestaltung der Produktion viel mehr über die
Eigenschaften der Nachfrage wissen.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
2 / 35
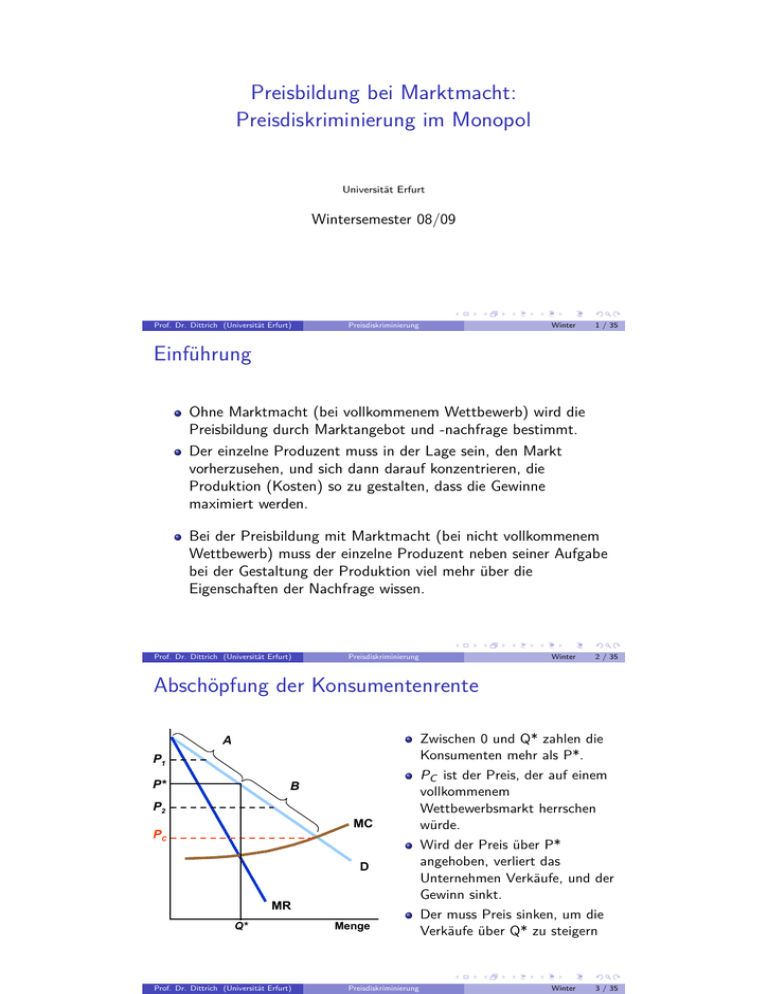
Abschöpfung der Konsumentenrente
Zwischen 0 und Q* zahlen die
Konsumenten mehr als P*.
A
P1
P*
B
P2
MC
PC
D
MR
Q*
Prof. Dr. Dittrich (Universität Erfurt)
Menge
Preisdiskriminierung
PC ist der Preis, der auf einem
vollkommenem
Wettbewerbsmarkt herrschen
würde.
Wird der Preis über P*
angehoben, verliert das
Unternehmen Verkäufe, und der
Gewinn sinkt.
Der muss Preis sinken, um die
Verkäufe über Q* zu steigern
Winter
3 / 35
Abschöpfung der Konsumentenrente
A
P*Q*: MC=MR
P1
P*
A: Konsumentenrente bei P*
B
MC
B: P>MC und Konsument
würde zu einem niedrigeren
Preis kaufen.
D
P1: geringere Verkäufe und
Gewinne
P2
PC
P2: Steigerung der Verkäufe
und Reduzierung der Gewinne
MR
PC: Wettbewerbspreis
Menge
Q*
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
4 / 35
Abschöpfung der Konsumentenrente
A
P1
P*
B
P2
MC
PC
D
MR
Q*
Prof. Dr. Dittrich (Universität Erfurt)
Frage: Wie kann das Unternehmen
die Konsumentenrente in A
abschöpfen und rentabel in B
verkaufen?
Antwort:
Preisdiskriminierung
Zweistufige Gebühren
Bündelung
Menge
Preisdiskriminierung
Winter
5 / 35
Winter
6 / 35
Übersicht
Abschöpfung der Konsumentenrente
Preisdiskriminierung
Intertemporale Preisdiskriminierung
Zweistufige Gebühren
Bündelung
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Preisdiskriminierung
. . . bedeutet, dass Firmen ein identisches Produkt zu
unterschiedlichen Preisen anbieten. Z.B. abhängig von
I
I
I
Menge
Nachfrage (Happy Hour, “Kinotag”, Saisonzuschlag,
last-minute Angebot)
Zugehöhrigkeit zu einer Personengruppe (Kinder- und
Seniorenrabatt)
Eine notwendige Voraussetzung zur Preisdiskriminierung ist, dass
die Firma Marktmacht besitzt.
Ein Monopolist kann u.U. (anders als eine Firma im
vollkommenen Wettbewerb) sein Produkt zu unterschiedlichen
Preisen anbieten.
Kann der Monopolist nur einen Preis setzen, so ist dieser so
hoch, dass ein ineffizientes Outputniveau entsteht.
Durch Preisdiskriminierung kann der Monopolist sowohl seinen
Gewinn steigern als auch den Wohlfahrtsverlust mindern.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
7 / 35
Arten der Preisdiskriminierung
Preisdiskriminierung ersten Grades
Von jedem Konsumenten wird ein individueller Preis verlangt: der
maximale bzw. Reservationspreis, den der Kunde zu zahlen bereit ist.
Preisdiskriminierung ersten Grades wird auch perfekte
Preisdiskriminierung genannt.
Preisdiskriminierung zweiten Grades
Der Preis hängt von der gekauften Menge, nicht aber vom Käufer ab.
Preisdiskriminierung zweiten Grades wird auch
Mengendiskriminierung genannt.
Preisdiskriminierung dritten Grades
Der Preis hängt von der Käufergruppe ab, der der Käufer angehört,
ist aber für jedes Mitglied der Gruppe identisch.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
8 / 35
Perfekte Preisdiskriminierung
Ohne Preisdiskriminierung beträgt der Output Q*, und der Preis ist
gleich P*. Der variable Gewinn entspricht der Fläche zwischen MC
und MR (gelb).
Die Konsumentenrente ist gleich der Fläche über P* und zwischen 0
und dem Output Q*.
Pmax
€/Q
MC
P*
PC
D = AR
MR
Q*
Prof. Dr. Dittrich (Universität Erfurt)
Q**
Menge
Preisdiskriminierung
Bei perfekter Diskriminierung,
zahlt jeder Konsument den
maximalen Preis, den er zu
zahlen bereit ist.
Die Gütermenge steigt auf Q**
und der Preis der letzten
Einheit sinkt auf PC , bei dem
gilt, MC = MR = AR = D. Die
Gewinne steigen um die Fläche
über MC zwischen altem MR
und D bis zu Output Q** (lila).
Winter
9 / 35
Perfekte Preisdiskriminierung
Wenn der Monopolist die Zahlungsbereitschaft jedes einzelnen
Kunden kennt, kann er diese als Preis verlangen.
Bei perfekter Preisdiskriminierung stimmt die marginale
Ertragskurve mit der Preiskurve überein (MR=D=p).
Dadurch schöpft der Monopolist die gesamte Konsumentenrente
ab. Der Konsument hat keinen Gewinn aus dem Handel.
Die umgesetzte Outputmenge ist effizient.
Es gibt keinen Wohlfahrtsverlust.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
10 / 35
Perfekte Preisdiskriminierung
Perfekte Preisdisk
Perfekte Preisdiskriminierung
• vollkommener Wettbewerb
Vollkommener Wettbewerb
I
I
I
I
I
⇒ Gleichgewicht bei eC (dort wo
⇒ CS = A+B+C und PS = D+E
⇒ kein Wohlfahrtsverlust
⇒ Markt effizient (weil p=MC)
Gleichgewicht bei ec ,
p=MC
CS = A+B+C
• Monopol (ohne Preisdiskrimi
PS = D+E
⇒ Gleichgewicht bei MR=MC ⇒
kein Wohlfahrtsverlust ⇒ CS = A und PS = B+D
Markt effizient, da p=MC⇒ Wohlfahrtsverlust C+E
⇒ Markt ineffizient (weil pS>MC
Mikroökonomie 1: 2. Preisdiskriminierung
Prof. Dr. Dittrich (Universität Erfurt)
Prof. Dr. Bettina Rockenbach
13
Preisdiskriminierung
Mikroökonomie 1: 2. Preisdiskriminierung
Winter
11 / 35
Perfekte Preisdiskriminierung
Perfekte
Preisdiskriminierung
• Monopol (mit perfekter Preisdiskriminie-
Mengendiskrim
rung)
Perfekte Preisdisk
Perfekte
Preisdiskriminierung
⇒ MR =Grenzerlös bei perfekter
Mengendiskriminierung
d
• vollkommener Wettbewerb
Preisdiskriminierung = Nachfragekurve
⇒ Gleichgewicht bei eC (dort wo
⇒ Einheit 1 wird zum Preis p1 mit Gewinn pMonopol
1–
ohne
⇒ CS = A+B+C und PS = D+E
Qd ,
MC1 verkauft, usw. bis zur letzten Einheit Preisdiskriminierung
⇒ kein Wohlfahrtsverlust
die zum Preis pC mit MC = MRd (also Gewinn
I Gleichgewicht bei e ,
s
⇒ Markt effizient (weil p=MC)
0) verkauft wird
MR=MC
⇒ CS = 0 und PS = A+B+C+D+E
I CS = A
• Monopol (ohne Preisdiskrimi
⇒ kein Wohlfahrtsverlust
I PS = B+D
⇒ Gleichgewicht bei MR=MC ⇒
⇒ Markt effizient (weil pC=MCC für die letzte
I Wohlfahrtsverlust: C+E
Einheit)
⇒ CS = A und PS = B+D
I Markt ineffizient, da
⇒ Wohlfahrtsverlust
Mikroökonomie 1: 2. Preisdiskriminierung
Prof. Dr. Bettina Rockenbach
15
Mikroökonomie
1: 2. Preisdiskriminierung C+E
ps > MCs
⇒ Markt ineffizient (weil p >MC
S
Mikroökonomie 1: 2. Preisdiskriminierung
Prof. Dr. Dittrich (Universität Erfurt)
Prof. Dr. Bettina Rockenbach
Preisdiskriminierung
13
Mikroökonomie 1: 2. Preisdiskriminierung
Winter
12 / 35
⇒ CS = A+B+C und PS = D+E
Perfekte
⇒ keinPreisdiskriminierung
Wohlfahrtsverlust
⇒ MarktPreisdiskriminierung
effizient (weil p=MC)
Perfekte
Perfekte Preisdisk
• vollkommener Wettbewerb
⇒ Gleichgewicht bei eC (dort wo
⇒ CS = A+B+C und PS = D+E
⇒ kein Wohlfahrtsverlust
⇒ Markt effizient (weil p=MC)
• Monopol (ohne Preisdiskriminierung)
Monopol mit perfekter
⇒ Gleichgewicht bei MR=MC ⇒Preisdiskriminierung
QS und pS
I MR ≡ D
d
⇒ CS = A und PS = B+D
I CS = 0
I PS = A+B+C+D+E
⇒ Wohlfahrtsverlust C+E
• Monopol (ohne Preisdiskrimi
I kein Wohlfahrtsverlust
⇒ Gleichgewicht bei MR=MC ⇒
⇒ Markt ineffizient (weil pS>MCS)I
Markt effizient, da
⇒ CS = A und PS = B+D
pc = MCc für die letzte ⇒ Wohlfahrtsverlust C+E
Prof.
Dr. Bettina Rockenbach
14
Einheit
⇒ Markt ineffizient (weil pS>MC
Mikroökonomie 1: 2. Preisdiskriminierung
rfekte Preisdiskriminierung
Mikroökonomie 1: 2. Preisdiskriminierung
Prof. Dr. Bettina Rockenbach
13
Mikroökonomie 1: 2. Preisdiskriminierung
ommener Wettbewerb
eichgewicht bei eC (dort
p=MC)
Prof.wo
Dr. Dittrich
(Universität Erfurt)
Preisdiskriminierung
Perfekte Preisdiskriminierung
S = A+B+C und PS = D+E
Mengendiskriminierung
in Wohlfahrtsverlust • Monopol (mit perfekter Preisdiskriminierung)
arkt effizient (weil p=MC)
Winter
13 / 35
Mengendiskriminierung
Mengendiskriminierung
⇒ MRd=Grenzerlös bei perfekter
Mengendiskriminierung
Preisdiskriminierung
= Nachfragekurve
⇒ Einheit 1 wird zum Preis p1 mit Gewinn p1 –
opol (ohne Preisdiskriminierung)
MC1 verkauft, usw. bis zur letzten Einheit Qd ,
die
eichgewicht bei MR=MC ⇒zum
QS Preis
und ppCS mit MC = MRd (also Gewinn
0) verkauft
wird
S = A und PS = B+D ⇒ CS = 0 und PS = A+B+C+D+E
ohlfahrtsverlust C+E ⇒ kein Wohlfahrtsverlust
⇒ Markt
effizient (weil pC=MCC für die letzte
arkt ineffizient (weil pS>MC
S)
Einheit)
Mikroökonomie 1: 2. Preisdiskriminierung
e 1: 2. Preisdiskriminierung
Prof. Dr. Bettina Rockenbach
Mikroökonomie 1: 2. Preisdiskriminierung
Prof. Dr. Dittrich (Universität Erfurt)
Prof. Dr. Bettina Rockenbach
Mengendiskrim
Keine Preisdiskriminierung
15
Mikroökonomie 1: 2. Preisdiskriminierung
14
Preisdiskriminierung
Prof. Dr. Bettina Rockenbach
Winter
16
14 / 35
Mengendiskriminierung
Mengendiskriminierung
Mengendiskriminierung
e 1: 2. Preisdiskriminierung
Keine Preisdiskriminierung
Prof. Dr. Bettina Rockenbach
Prof. Dr. Dittrich (Universität Erfurt)
16
ohne Mengendiskriminierung
Konstante Grenzkosten,
MC=m=30
30 Einheiten für 60
CS = E = 450
PS = F = 900
W = 1350; Wohlfahrtsverlust
= G = 450
Preisdiskriminierung
Winter
15 / 35
Mengendiskriminierung
Mengendiskriminierung
Mengendiskriminierung
Keine Preisdiskriminierung
Konstante Grenzkosten,
MC=m=30
Mengendiskriminierung: 20
Einheiten für 70, weitere 20
Einheiten für 50
CS = A+C = 400
PS = B = 1200
W = 1600; Wohlfahrtsverlust
= D = 200
Prof. Dr. Dittrich (Universität Erfurt)
Mikroökonomie
1: 2. Preisdiskriminierung
Preisdiskriminierung
Winter
Prof. Dr. Bettina Rockenbach
16 / 35
16
Mengendiskriminierung
Durch Mengendiskriminierung verkauft das Monopol mehr
Einheiten und macht einen größeren Gewinn.
Die Wohlfahrt steigt.
Die Kosumentenrente sinkt.
Je mehr Preisblöcke der Monopolist setzt, desto dichter kommt
er an die perfekte Preisdiskriminierung heran.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
17 / 35
Mengendiskriminierung
...als optimale Lösung des Monopolisten
Angenommen, es gibt 2 Typen von Kunden mit bekannten
Zahlungsbereitschaften (zu gleichen Anteilen an der
Gesamtkundenschaft).
Der Typ ist private Information (hidden information).
Der Monopolist will mit Preisdiskriminierung 2. Grades seinen
Profit maximieren.
Er bietet folgende Preis-Mengen Kombinationen an:
S = (T1 , x1 ), (T2 , x2 ), (0, 0) mit x1 , x2 ≥ 0
Die Konsumenten wählen ihr (Ti , xi ), welches ihre
Konsumentenrente maximiert.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
18 / 35
Mengendiskriminierung
...als optimale Lösung des Monopolisten
Annahmen:
A1 Stückkosten sind konstant und normalisiert zu 0.
A2 Der Monopolist maximiert seinen Profit:
π = T1 + T2
und die Konsumenten ihre Rente:
Ui (x , T ) =
38
Z x
0
Pi (y )dy − T
A3 Pi (x ) ist stetig differenzierbar mit P
A4 (Single–Crossing) For all x
Pi (0) > 0 und ∃ {x |Pi (x ) = 0 und i
P2 (x) > P1 (x).
∀i = 1, 2
Monopoly
0
(x ) < 0, es gilt auch
∈ {1, 2}}
(1.33)
A4 is called “single–crossing” assumption for the following reason: Pick
an arbitrary point in (x, T ) space, say x1∗ , T1∗ , and draw the two types’ indifProf. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
ference curves that pass through this point. Since the slope of indifference
curves is equal to Pi (x), A4 assures that these curves cross only once at this
given point, as illustrated in Figure 1.7.
Winter
19 / 35
Winter
20 / 35
Mengendiskriminierung
Indifferenzkurven der Konsumenten
T
6
T2∗
T2∗∗
Tˆ2
T1∗
T1∗∗
•
....... ....... ....... ....... ....... ....... ....... ....... ....... ....... ..................................................
.
.........
.........
.......
.......
......
....
..... 2
......
.....
.....
.....
.....
.
.
.
.
.
....
...
..
.
.
....
.
...
....
.
.
.
.. .
...
.
.
.
.
....... ....... ....... ....... ....... ....... ......... ....... ....... ....... .........................................
.
.
.
.
.
.
.
.
.
.
.
.
..
........ . . . . .... . . . . . .............
.
.
.
.
.
.
...
...... . . . . . . . . . .....
...
...... . . . . . . . . . .. . . . . . . . . . . .....
...
..... . . . . . ... . . . . . .......
.... . . . . . . . . . . . .
...
...
...
.... . . . . . . . . . . . .
..
...
....... ....... ....... ....... ........... ....... ....... .............. ............ ............ ............................................................... .. . .. .
...
.. . . . . . .......... . . . . ...........
..
...
..
.... . . . . . . . ................. . . . . . .... . . . . . . .............
.
.
... . . . . . . . ............ . . . . . . . . ... . . . . . . . ........
..
.
.
.....
.. . . . . . . . ......... . . . . . . . . . . ... . . . . . . .
..
.
.
.
....
....
..
... . . . . . . .......... . . . . . . . . . . . . .... . . . . . .
.
.
....
..
... . . . .... . . . . . . . . . . .
....
..
.. . . . ... . . . . . . . .. . . .
....
..
... . . . . . ...... . . . . . . . . . . . . . . . .... . . . . .
...
... . . ...... . . . . . . . . . . .
..
...
....... ....... .......... ....... ....... ................................................................... . . . . . . . . . . . . . ... . . . .
.
.
.
.
.
.
.
.
.
.
.......... . . . . . .. . . .
..
...
......... . . . . . . . . . . .
.
....... ....... ......... ....... .....................
.
...... . . . . . .
.. ..
.. .....
.
.
.
..
.
.
.
.
.
.
.
.
....... . . . . . .. . .
... .
..
..... . . .. .
... ..
..... .. ..
...
..... . . . .
..... .... .
...
..
........ . .... .
.....
.... .. .
... .....
..
...
.... .
... .......
.
.
......
.
.
.. ......
.
.
.....
.
.
.
.
.
.
....
.. .....
.
.
..
.
.
.. .....
.
.
.
.... ...... 1
.
.
.
.
.
..
........
.
.....
. .....
.
.
.
.
.
.
.
.
.
.
...
.
..
..
..
...
........
.
...
...
.
.
.
.
.
.
.
.
.
...
...
...
...
...
•
•
•
•
-
x1∗∗ x1∗
Annahmen:
A4 P2 (x ) ≥ P1 (x )
A5 2P10 (x ) ≤ P20 (x )
x
x2∗
Figure 1.7: Customers’ Indifference
Curves
Preisdiskriminierung
Prof. Dr. Dittrich (Universität Erfurt)
Mengendiskriminierung
Optimal Sales Plan The optimal sales plan maximizes π subject to the
following participation constraints
U1 (x1 , T1 ) ≥ U1 (0, 0) = 0
(1.34)
U2 (x2 , T2 ) ≥ U2 (0, 0) = 0
(1.35)
Das optimale Menü erfüllt die Partizipationsbedingungen
U1 (x1 , T1 ) ≥ U1 (0, 0)
U2 (x2 , T2 ) ≥ U2 (0, 0)
und ist anreizkompatibel
U1 (x1 , T1 ) ≥ U1 (x2 , T2 )
U2 (x2 , T2 ) ≥ U2 (x1 , T1 )
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
21 / 35
Mengendiskriminierung
Das optimale Menü schöpft die gesamte Konsumentenrente von
Typ 1 ab:
T2 =
Z x1
0
P1 (y )dy
Typ 2 zahlt das gleiche für die ersten x1 Einheiten und seine
maximale Zahlungsbereitschaft für die zusätzlichen Einheiten
x2 − x1 :
T2 = T1 +
Z x2
x1
P2 (y )dy
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
22 / 35
Winter
23 / 35
Winter
24 / 35
Mengendiskriminierung
Der Monopolist maximiert also seinen Gewinn mit
max
x1 ,x2 >0
Z x1
2
0
P1 (y )dy +
Z x2
x1
P2 (y )dy
im Optimum gilt:
2P1 (x1 ) − P2 (x1 ) ≤ 0 und (...)x1 = 0
P2 (x2 ) ≤ 0 und P2 (x2 )x2 = 0
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Mengendiskriminierung
Das optimale Menü beinhaltet keine Verzerrung für Typ 2
P2 (x2 ) = 0
x2 > 0
Das optimale Menü ist monoton
x2 > x1
T2 > T 1
Es gibt eine Verzerrung für Typ 1
P1 (x1 ) > 0
Typ 1 hat eine Konsumentenrente von 0
U1 (x1 , T1 ) = 0
Typ 2 hat eine Rente, wenn x1 > 0
U2 (x2 , T2 ) > 0
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
was already provided in Lemma 1.1). That surplus is always lowered if one
deviates from the efficient level of x1 .
Mengendiskriminierung
Optimal Sorting
Pi (x), φ(x)
6
1 ..........................................
...................
... ....................
... .....................
... ........................
... ..........................
... ...........................
... .......................................
... ................................
... ...................... ........
.......
..
...
.
.......
... ................................
.......
.................
...
.......
..............
...
.......
.
..........
...
.......
.......
.........
...
.......
........
...
.......
......
...
.......
.....
...
.......
.
. ......
...
.......
.
.
.
.......
...
. ......
.......
....... P2 (x)
φ(x) ....... ... ........... P1 (x)
.......
.....
.......
... .
.......
.....
...
.......
.....
.....
.......
.....
...
...
•
x1 =
2
3
1
•
- x
x2 = 2
Figure 1.8: Optimal Sorting with Two Customers if Pi (x) := 1 − 1i x
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
25 / 35
Mengendiskriminierung
1.4.4
Sorting, Bunching, and Exclusion
Finally, note that it is not always optimal to serve both customers and discriminate between them. Depending upon the properties of inverse demand
functions, it may be optimal to either not serve the low type at all, and exUnter serve
den Annahmen
A1 bis
gibt
es in
demthe
Modell
zwei Fälle:
clusively
the high type,
or A5
treat
both
types
same.
Altogether,
Sortingthe optimal price discrimination falls into either one of three
categories:
1. “Sorting” or true discrimination, with 0 < x1 < x2 , T1 < T2 .
0 < x1 < x2 ; T1 < T2
2. “Bunching” or no discrimination, with x1 = x2 > 0, T1 = T2 .
Exclusion (extreme Diskriminierung)
3. “Exclusion” where only the high type is served at a price equal to its
maximum willingness to pay, 0 = x1 < x2 , T2 > T1 = 0.
0 = x1 < x2 ; 0 = T1 < T2
Note carefully that Proposition 1.2 excludes neither case.
Example 1.5 Here we illustrate that all three cases may occur.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
26 / 35
Preisdiskriminierung 3. Grades
Typischerweise kennt eine Firma nicht die individuelle
Zahlungsbereitschaft jedes Kunden. Sie kann jedoch abschätzen,
welche Kundengruppen eine höhere Zahlungsbereitschaft haben.
Bsp. Flugpreise
I
Unterschiede der Elastizitäten geben an, dass manche
Konsumenten bereit sind, einen höheren Flugpreis zu zahlen als
andere.
F
F
I
Geschäftsreisende haben nur eine geringe Auswahl und ihre
Nachfrage ist weniger elastisch.
Die Freizeitreisenden haben eine größere Wahlfreiheit und sind
preisempfindlicher.
Die Fluggesellschaften teilen den Markt in Gruppen ein, indem
sie verschiedene Beschränkungen für die Tickets festlegen.
F
F
Preiswerter: Voranmeldung, Wochenendaufenthalt, keine
Rückerstattung
Teuerste Kategorie: keine Beschränkungen
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
27 / 35
Preisdiskriminierung 3. Grades
Angenommen, der Monopolist verkauft an zwei Gruppen von
Konsumenten und diskriminiert den Preis zwischen den beiden
Gruppen dadurch, dass er auf beiden Märkten unterschiedliche
Mengen anbietet.
Bsp.: Zwei Märkte befinden sich in unterschiedlichen Ländern.
Preisdiskriminierung zwischen USA und Europa:
Preisdiskriminierung
3. Grades
Prozentsatz, zu dem Produkte in Europa teurer
sind als in den
I
USA (1999)
Levi’s Jeans
GB
75%
51%
D
87%
20%
F
60%
45%
• Konstante marginale und
CDs durchschnittliche
Kosten von m
• Markt 1 (Q1 Einh. zu p1) ⇒
Profit
p1Q1 – mQ1
Preisdiskriminierung
3. =Grades
Beispiel
•EinMarkt
2 (Q2 Einh.
zu p2) ⇒ Kosten von m
Konstante marginale
und durchschnittliche
Markt 1
Profit = p2Q2 – mQ2
Q1 Einheiten zum Preis p1
Profit = p1 Q1 − mQ
• Gesamtprofit
=1 p1Q1 – mQ1 + p2Q2 – mQ2
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
28 / 35
Markt 2
Q2 Einheiten zum Preis p2
Profit = p2 Q2 − mQ2
Gesamtprofit
= p1 Q1 − mQ1 + p2 Q2 − mQProf.
2
Mikroökonomie
1: 2. Preisdiskriminierung
Dr. Bettina Rockenbach
Wie werden Q1 und Q2 zur Maximierung des Gesamtgewinns
gewählt?
Da die Märkte unabhängig voneinander sind, werden Q1 und Q2
so gewählt, dass in jedem Markt MR=m gilt:
MR1 = m = MR2
Preisdiskriminierung 3. Grades
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
29 / 35
Preisdiskriminierung 3. Grades
Markt 1
Prof. Dr. Dittrich (Universität Erfurt)
Markt 2
Preisdiskriminierung
Winter
30 / 35
21
Preisdiskriminierung 3. Grades
In welchem Markt verlangt der Monopolist einen höheren Preis?
Monopolmacht, Elastizität und Preisaufschlag:
δR
δ(PQ)
=
δQ ! δQ !
Q
δP
δP
=P +P
MR = P + Q
δQ
P
δQ
!
!
P
δQ
ED =
Q
δP
!
!
1
Q
∆P
=
ED
P
∆Q
1
MR = P + P
ED
MR =
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
31 / 35
Monopolmacht und Preisaufschlag
Der Gewinn π wird bei MR = MC maximiert
1
P +P
= MC
ED
1
P 1+
= MC
ED
MC
P=
1 + E1D
Der Preisaufschlag über MC als Prozentsatz des Preises:
1
MC
1+
=
ED
P
1
MC − P
1
P − MC
=
⇒ −
=
ED
P
ED
P
1
− ED ist der Preisaufschlag über MC als Prozentsatz des Preises.
Der Preisaufschlag eines Monopolisten ist gleich dem Kehrwert der
Elastizität der Nachfrage.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
32 / 35
Preisdiskriminierung 3. Grades
Ein Beispiel
In welchem Markt verlangt der Monopolist einen höheren Preis?
MR1 (q1? ) = m = MR2 (q2? ), also:
p1 (q1 ) 1 +
1
1
= p2 (q2 ) 1 +
ED1
ED2
Daher p1 (q1 ) > p2 (q2 ), nur wenn
1
1
1+
< 1+
→ ED1 > ED2
ED1
ED2
Der Monopolist setzt den höheren Preis in dem Markt, in dem
die Nachfrage am wenigsten elastisch ist.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
33 / 35
Preisdiskriminierung 3. Grades
Ein Beispiel
Die Nachfrage in Markt 1 sei elastischer als
in Markt 2: ED1 = −3; ED2 = −2.
Dann ist MR1 = MR2 ⇔ p1 = 3/4p2
z.B. p1 = 15 und p2 = 20
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
34 / 35
Preisdiskriminierung 3. Grades
Preisdiskriminierung 3. Grades ist ineffizient und führt zu
Wohlfahrtsverlusten.
I
I
Preisdiskriminierung 3. Grades
W = CS + PS = CS1 + CS2 + π1 + π2
Wohlfahrtsverlust = DWL1 + DWL2
Vollkommener Wettbewerb:
W = CS1 + CS2 + π1 + π2 + DWL1 + DWL2
Im Vergleich zum Monopol ohne Preisdiskriminierung kann die
Wohlfahrt in einem Monopol mit Preisdiskriminierung 3. Grades
sowohl höher als auch niedriger sein.
Prof. Dr. Dittrich (Universität Erfurt)
Preisdiskriminierung
Winter
35 / 35