1 Tutorium – Mikroökonomik II für Klausur(wiederholer) – Sitzung 1
Werbung

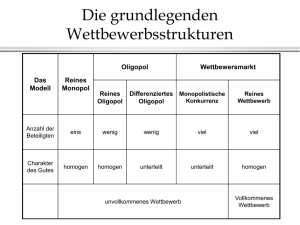
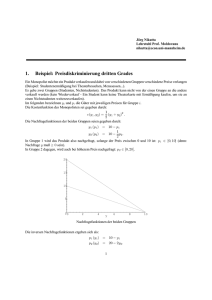
Anton Parlow, Montag (9.7.), 18-20 Uhr, 4.18.009 Isabel Pesch,, Montag (9.7.), 14-16 Uhr, 4.18.009 Tutorium – Mikroökonomik II für Klausur(wiederholer) – Sitzung 1 Aufgabenkomplex: Totales Gleichgewicht / Edgeworth Box 1. Betrachten Sie eine Volkswirtschaft mit 2 Unternehmen, die 2 Güter (X und Y) unter Einsatz von 2 Produktionsfaktoren (K und L) produzieren. a) Wie lauten die Bedingungen für eine effiziente Produktion? Wie sieht die Situation in einer Edgeworth-Box aus? b) Was ist die „Kontraktkurve“? Was ist eine pareto-optimale Situation? Wie lässt sich aus der Kontraktkurve die Transformationskurve konstruieren? . c) Können Verteilungen, bei denen ein Individuum nichts und ein anderes Individuum alles hat, pareto-optimal sein? 2. Robinson und Freitag leben auf einer Insel. Robinson besitzt 30 Kokosnüsse und 10 Fische. Freitag dahingegen besitzt 40 Fische und 5 Koskosnüsse. Die Preise werden in Kokosnüssen pro Fisch gemessen. a)Wie sieht die Situation in einer Edgeworth-Box aus? Wie sieht das Gleichgewicht aus? Was ist die Tauschkurve für Robinson? b) Robinson hat eine Grenzrate der Substitution von 4 Kokosnüssen je Fisch, während Freitag eine Grenzrate der Substitution von 1/3 Kokosnüssen je Fisch hat. Ist die Verteilung paretooptimal? c) Sollten beide miteinander handeln? Wenn ja, wer sollte welches Gut kaufen und welches Gut verkaufen? Welches Preisverhältnis wird sich einstellen? Aufgabenkomplex 2: Multiple Choice – Aufgaben Richtig Falsch Der Satz von Walras lässt sich nur auf Modelle mit zwei Märkten anwenden Im allgemeinen Gleichgewicht addieren sich die Überschussnachfragen aller Haushalte nach einem Gut zu Null Eine pareto-optimale Güterallokation wird durch Verteilungsgerechtigkeit begründet 1 Anton Parlow, Dienstag (10.7.), 16-18 Uhr, 4.18.009 Isabel Pesch,, Mittwoch (11.7.), 14-16 Uhr, 4.18.008 Tutorium – Mikroökonomik II für Klausurwiederholer – Sitzung 2 Aufgabenkomplex: Externe Effekte und Wohlfahrtstheorie 1. Externe Effekte a) Was sind externe Effekte? Erkläre anhand von Beispielen! b) Bei der Produktion eines Gutes falle proportional zur produzierten Menge X ein Schadstoff an, der unkontrolliert an die Umwelt abgegeben wird. Das Unternehmen kann für den Schaden nicht haftbar gemacht werden, so dass die Gesellschaft die entstehenden Kosten mehr oder minder gleichmäßig tragen muss. Handelt es sich um einen externen Effekt? Was sind die Wohlfahrtswirkungen? Bitte anhand einer Grafik erläutern! c) Bei der Produktion eines Gutes seien die sozialen Kosten niedriger als die privaten Kosten des Unternehmens. Was ist der Unterschied zwischen dem privaten Gleichgewicht und der wohlfahrtsoptimalen Allokation? Was sind die Wohlfahrtswirkungen? Bitte grafisch erklären! 2. Wohlfahrtstheorie a) Welche Wohlfahrtsfunktionen beschreiben Rawls und Bentham? b) Zwei Haushalte A und B werden durch folgende Nutzenfunktionen beschrieben: UA=XA UB=2XB Wobei XA und XB die Mengen sind, welche die Haushalte von einem homogenen Gut konsumieren. Wie ist die wohlfahrtsmaximierende Aufteilung wenn die Gesamtgütermenge 600 Einheiten beträgt und die Wohlfahrtsfunktion vom Rawls-Typ und Bentham-Typ ist? c) Was versteht man unter Konsumenten – und Produzentenrente? d) Vergleiche anhand einer Grafik das Marktgleichgewicht bei vollständiger Konkurrenz mit dem Angebotsmonopol, hinsichtlich der Konsumentenrente, Produzentenrente und Wohlfahrt. Die zugrunde liegende Grenzkosten, Grenzerlös und Preis-Absatz-Funktionn sind linear. Aufgabenkomplex: Multiple Choice – Aufgaben Richtig Falsch Das Vorliegen externer Effekte verhindert eine pareto-optimale Allokation. Im Bereich fallender Durchschnittskosten realisiert das Unternehmen bei Grenzkostenpreissetzung einen Verlust Bei abnehmenden Grenznutzen fordern sowohl Bentham als auch Rawls eine Gleichverteilung des Einkommens im Wohlfahrtsoptimum 1 Isabel Pesch,, Montag (16.07.), 14-16 Uhr, 4.18.009 Anton Parlow, Montag (16.07.), 18-20 Uhr, 4.18.009 Tutorium – Mikroökonomik II – Sitzung 3 Aufgabenkomplex: Monopol 1. Monopol Gegeben sei ein Gütermarktmonopol. Die Nachfragefunktion lautet q = 1 − p und die Kostenfunktion K = kq a) Wie hoch ist die abgesetzte Menge und der Güterpreis? b) Wie hoch ist der Gewinn des Monopolisten? 2. Wohlfahrtswirkungen Vergleiche anhand einer Grafik das Marktgleichgewicht bei vollständiger Konkurrenz mit dem eines Angebotsmonopols hinsichtlich Konsumentenrente, Produzentenrente und Wohlfahrt. Angenommen sind lineare Grenzkosten, Grenzerlöse und Nachfragefunktionen 3. Preisdiskriminierung Gegeben ist ein Gütermarktmonopol. Die Nachfragefunktion lautet q = a − bp mit a,b > 0 und die Kostenfunktion sei K = kq + K f a) Bestimme Absatzmenge und Güterpreis im Gewinnmaximum, wenn keine Preisdiskriminierung möglich ist b) Nehme an, der Monopolist könnte perfekt preisdiskriminieren. Wie hoch wäre die abgesetzte Menge und wie hoch der Preis der letzten verkauften Gütereinheit? c) Vergleiche anhand einer Grafik die Lösungen mit / ohne Preisdiskriminierung im Hinblick auf den Gewinn des Monopolisten, die Konsumentenrente und die gesamte Wohlfahrt. Aufgabenkomplex: Multiple-Choice-Aufgaben Richtig Falsch Setzt das natürliche Monopol Preise gemäß den Grenzkosten, wird es Verluste erwirtschaften Wenn die Vorraussetzungen für Preisdiskriminierung erfüllt sind, ist es für einen Monopolisten immer gewinnerhöhend, sie auch anzuwenden Ein Monopolist setzt immer eine Menge fest, die im elastischen Bereich seiner Preis-Absatz-Funktion liegt. Bei Preisdifferenzierung wird ein Monopolist von der Nachfragergruppe den höheren Preis fordern, die die elastischere Nachfrage besitzt. Ist der gewinnmaximale Output eines Monopols durch die Regel Preis = Grenzkosten bestimmt? Falls ein Monopol seinen Absatzmarkt in vier Teilmärkte aufspalten kann, liegt dann eine Preisdiskriminierung vierten Grades vor? Sind Mengenrabatte eine Form der Preisdiskriminierung zweiten Grades? Falls ein Monopol seinen Absatzmarkt in räumlich in zwei Teilmärkte aufspalten kann und die Preiselastizität der Nachfrage auf beiden Teilmärkten überall gleich ist, kann er dann unterschiedliche Preise verlangen? 1 2 Isabel Pesch,, Mittwoch (18.07.), 14-16 Uhr, 4.18.008 Anton Parlow, Dienstag (17.07.), 16-18 Uhr, 4.18.009 Tutorium – Mikroökonomik II – Sitzung 4 Aufgabenkomplex: Cournot-Dyopol 1. Cournot-Dyopol Gegeben sei ein Cournot-Dyopol. Die Nachfragefunktion lautet q = 1 − p mit und die Kostenfunktion K = kqi mit i=1,2. a) Bestimme die Reaktionsfunktion beider Firmen, die gleichgewichtige Absatzmenge einer Firma, den Güterpreis und den Gewinn pro Firma. b) Wie groß ist die gesamte produzierte Menge und Preis, wenn die Unternehmen ein Kartell bilden? c) Wie groß wäre der Gewinn für Firma 1, wenn beide jeweils die Hälfte im Kartell produzieren? Ist ein solches Kartell stabil? (Tipp: Auszahlungsmatrix) 2. Und schon wieder Cournot-Dypol Gegeben sei ein Cournot-Dyopol. Die Nachfragefunktion lautet p = a − bx mit x = x1 + x2 . Die Kostenfunktion ist identisch für jede Firma und lautet Ci = cxi mit i=1,2. a) Leite die Reaktionsfunktionen beider Unternehmen her und zeichne sie in ein Mengendiagramm. b) Wie hoch sind die produzierten Mengen und Preise? Zeichne das Gleichgewicht in dasselbe Diagramm und kennzeichne den Punkt mit C. 3. Stackelberg-Oligopol Nutze die Information aus Aufgabe 2 und bestimme die gleichgewichtige Menge für Firma 1, wenn diese Stackelberg-Führer ist. Bitte kennzeichne das Gleichgewicht in derselben Grafik mit S und zeichne die Isogewinnlinien für beide Firmen in beiden Situationen. Aufgabenkomplex: Multiple-Choice-Aufgaben Richtig Falsch Im Cournot-Oligopol täuschen sich die Unternehmen bezüglich der Mengenreaktion der Konkurrenten Im Stackelberg-Oligopol haben zwei Unternehmen mit identischer Kostenfunktion auch die gleiche Angebotsmenge Im Oligopol ist die zur erfolgreichen Durchsetzung einer Preisdiskriminierung erforderliche Marktmacht nicht gegeben 1 2