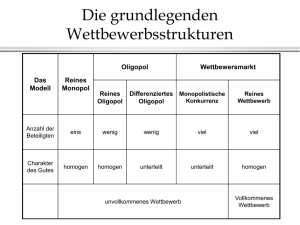
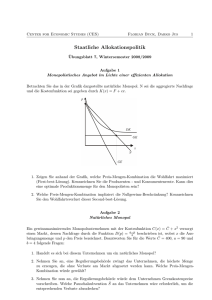
Das Monopol Gewinnmaximierung im Monopol Gewinnfunktion: π

Das Monopol
Gewinnmaximierung im Monopol
Gewinnfunktion:
π = E(x) − C(x)
(E: Ertrag und C: Gesamtkosten).
Aus
∂π
∂x
=0
⇒
E0 = C0 .
E, C, π
Kosten C
Erlös (Umsatz) E
Gewinn π
x
p
pM
Cournotscher Punkt
Grenzkosten C 0
Grenzerlös E 0
PAF
xM
Abbildung 1: Gewinnmaximierung im Monopol
x
Das Monopol bei linearer PAF
Erlösfunktion: E = p · x, wobei p durch die PreisAbsatz-Funktion p = a − bx zu ersetzen ist. Also:
E = (a − bx) · x = ax − bx2
Die Grenzerlösfunktion lautet dann
E0 =
∂E
= a − 2bx
∂x
Lineare Kostenfunktion ⇒ konstante Grenzkosten:
C = c · x + Cf
∂C
=c
∂x
Nach der Outputregel im Monopol E’=C’ erhalten
wir die optimale Menge:
C0 =
E0 = C0
⇒
a − 2bx = c
⇒
x∗ =
a−c
2b
und durch Einsetzen in die PAF den optimalen Preis
p∗ =
a−c
2
Monopolpreis und Elastizität (mathematisch)
Erlös hängt in zweifacher Weise von der Menge ab:
E(x) = x · p(x)). Grenzerlös (Produktregel):
E0 =
∂x
∂p
∂E
=
· p(x) +
·x
∂x
∂x
∂x
= 1 ist. Erweitert man den letzten Term
wobei ∂x
∂x
mit p, so ergibt sich
E0 = p + x ·
∂p x
∂p · p
=p+p·
·
∂x · p
∂x p
(6)
∂p
∂x
· xp ist aber genau der Kehrwert der Elastizität.
Wir können daher (6) durch Ausklammern von p auch
schreiben als
1
0
E =p 1+
(7)
ε
Dieser Ausdruck ist als Amoroso-Robinson-Relation
bekannt. In einigen Büchern wird sie auch mit “-” und
dem Betrag der Elastizität geschrieben. Berücksichtigt man nun, dass E 0 = C 0 gelten soll, so folgt aus
(7) durch auflösen nach p
p=
C0
1 + 1ε
als Regel für die Preissetzung (Markup-Pricing).
Monopolpreis und Elastizität (graphisch)
Im Monopol gilt, dass der Monopolist sein Optimum
immer im elastischen Bereich der PAF wählt.
p
= −∞
|| > 1
= −1
|| < 1
PAF
=0
E0
x
Aus der Abb. kann man dies sofort erkennen, da bei
einer Elastizität zwische 0 und -1 der Grenzerlös negativ wäre. Nach der Preissetzungsregel würde das aber
negative Grenzkosten implizieren, was nicht sinnvoll
ist.
Wohlfahrt im Monopol
Bei normalem Monopolverhalten (E 0 = C 0 ):
p
A
E
B
C
D
H
G
GK
F
P AF
0
xM
x
GE
Bei Regulierung (P = C 0 ):
p
A
E
B
C
D
H
G
GK
F
P AF
0
xM
GE
x
Preisdiskriminierung
Arten von Preisdiskriminierung:
Preisdiskriminierung ersten Grades: (Totale Preisdiskriminierung) Jeder Konsument zahlt einen
individuellen Preis, der seiner Zahlungsbereitschaft entspricht.
Preisdiskriminierung zweiten Grades: Der Preis variiert mit der abgenommenen Menge (z.B. Mengenrabatte), ist aber sonst für alle Konsumenten gleich.
Preisdiskriminierung dritten Grades: Der Monopolist bildet Marktsegmente anhand von eigenschaften des Konsumenten und bietet dann für
jedes Segment einen anderen Preis an. Beispiel:
Studentenpreise, Nachtzuschläge.