1. Beispiel: Preisdiskriminierung dritten Grades

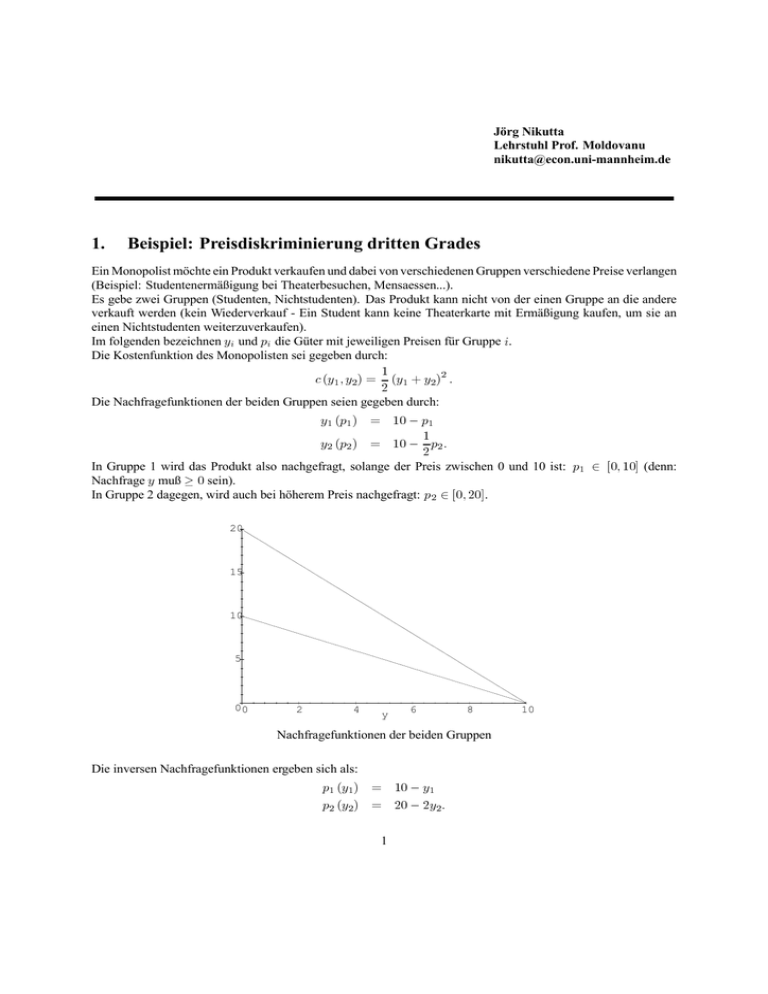
Jörg Nikutta
Lehrstuhl Prof. Moldovanu
[email protected]
1.
Beispiel: Preisdiskriminierung dritten Grades
Ein Monopolist möchte ein Produkt verkaufen und dabei von verschiedenen Gruppen verschiedene Preise verlangen
(Beispiel: Studentenermäßigung bei Theaterbesuchen, Mensaessen...).
Es gebe zwei Gruppen (Studenten, Nichtstudenten). Das Produkt kann nicht von der einen Gruppe an die andere
verkauft werden (kein Wiederverkauf - Ein Student kann keine Theaterkarte mit Ermäßigung kaufen, um sie an
einen Nichtstudenten weiterzuverkaufen).
Im folgenden bezeichnen |l und sl die Güter mit jeweiligen Preisen für Gruppe l.
Die Kostenfunktion des Monopolisten sei gegeben durch:
f +|4 > |5 , @
4
5
+|4 . |5 ,
5
=
Die Nachfragefunktionen der beiden Gruppen seien gegeben durch:
|4 +s4 ,
@
|5 +s5 ,
@
s4
4
43 s5 =
5
43
In Gruppe 1 wird das Produkt also nachgefragt, solange der Preis zwischen 0 und 10 ist: s4
Nachfrage | muß 3 sein).
In Gruppe 2 dagegen, wird auch bei höherem Preis nachgefragt: s5 5 ^3> 53`.
20
15
10
5
00
2
4
6
y
8
Nachfragefunktionen der beiden Gruppen
Die inversen Nachfragefunktionen ergeben sich als:
s4 +|4 ,
s5 +|5 ,
@
@
1
|4
53 5|5 =
43
10
5
^3> 43`
(denn:
Das Maximierungsproblem des Monopolisten ist generell:
pd{ s4 +|4 , |4 . s5 +|5 , |5
|4 >|5
In diesem Fall also:
pd{ +43
|4 >|5
f +|4> |5, =
|4, |4 . +53 |5 , |5 45 +|4 . |5,5 =
58
88
<3
Aus der Bedingung erster Ordnung ergibt sich die gewinnmaximale Lösung: |4 @ 48
: , |5 @ : , s4 @ : , s5 @ : .
73
55:8
Die produzierte Gesamtmenge ist also: |4 . |5 @ : r 8> :4= Der Gesamtgewinn des Monopolisten ist: 7< r
79> 76=
1.1
Ohne Preisdiskriminierung
Dasselbe Beispiel wie gerade mit dem einzigen Unterschied, daß der Monopolist einen einheitlichen Preis verlangen
muß. Die Gesamtnachfrage ist die Summe der Einzelnachfragen (NICHT DIE INVERSEN NACHFRAGEFUNKTIONEN ADDIEREN!):
| +s, @
45 s
53 6
5s
43
s 5 +43> 53`
=
s 5 ^3> 43`
Gesamtnachfragefunktion der beiden Gruppen
Die Nachfragefunktion hat dort einen ’’Knick’’, wo der Preis für die erste Gruppe zu hoch wird und diese nichts
mehr konsumieren möchte. Mathematisch bedeutet dies, daß die Funktion an dieser Stelle nicht differenzierbar
ist und man kann nicht einfach drauflos maximieren, sonderen muß sich die beiden Teile einzeln angucken. Man
berechnet das Maximum für den Fall, daß der Preis zwischen 0 und 10 ist und dann nochmal gesondert für den
2
Fall, daß der Preis zwischen 10 und 20 liegt. Anschließend vergleicht man, in welchem Fall der Gewinn des
Monopolisten größer ist - dies ist dann das Gewinnmaximum mit den entsprechenden | und s.
1.1.1
Fall: s 5 +43> 53`
Die inverse Nachfragefunktion ist (erneut): s +| , @ 53 5|. Das Maximierungsproblem des Monopolisten ist:
pd{ +53
|
5|, | 45 |5=
Die Bedingung erster Ordnung liefert: | @ 7, s @ 45. Daraus folgt ein Gewinn von @ 73.
Der gewinnmaximale Preis liegt tatsächlich in dem Intervall welches wir betrachten (43 ? 45 @ s 53)andernfalls würde es einen Widerspruch geben und man müßte versuchen, mittels eines Randchecks das zulässige Maximum zu bestimmen. Mit anderen Worten müßte man den Gewinn des Monopolisten für s @ 43 und
s @ 53 ausrechnen...
Wieso kommt hier eigentlich etwas anderes heraus als im Fall mit Preisdiskriminierung? Schließlich fragen
doch auch hier nur die Leute in dem einen Markt nach...? Oben maximiert der Monopolist zwar die gleiche
Erlösfunktion, aber in seine Kostenfunktion geht auch der Output ein, der für den anderen Markt produziert
wird (also nicht nur |5 , sondern auch |4 ). Das ist hier nicht der Fall, denn es gibt ja nur einen Markt.
1.1.2
Fall: s 5 ^3> 43`
Die inverse Nachfragefunktion ist: s +|, @ 73
6
56 |= Das Maximierungsproblem des Monopolisten ist:
73 5 4
pd{
6 | | 5 |5 =
6
|
533
Die Bedingung erster Ordnung liefert: | @ 73
: , s @ 54
r <> 85. Daraus folgt ein Gewinn von @ 6;> 3<.
Der Preis liegt auch hier im zulässigen Intervall... (selbe Überlegung wie oben)
ALSO: Der Monopolist wählt | @ 7, s @ 45 und erzielt einen Gewinn von @ 73=
1.2
Vergleich der beiden Beispiele
Ohne Preisdiskriminierung muß der Monopolist für alle den gleichen Preis setzen und kann nicht auf die Nachfragen der verschiedenen Gruppen eingehen. Mit Preisdiskriminierung wählt er für jede Gruppe ein eigenes Maximum. Daher ist es einleuchtend, daß er insgesamt im Fall von Preisdiskriminierung einen höheren Gewinn macht.
Genauer: Sein Gewinn kann nicht kleiner sein, als der ohne Preisdiskriminierung, denn im Zweifelsfall kann er für
beide Gruppen den gleichen Preis setzen und auf seine Preisdiskriminierung ’’verzichten’’.
Wenn man sich die Wohlfahrt (also die Summe der Konsumenten- und Produzentenrente) in beiden Fällen anschaut,
stellt man fest, daß die Möglichkeit der Preisdiskriminierung zu einer Steigerung der Wohlfahrt führen kann.
3