Document

Mikroökonomik
Monopol und Monopson
Harald Wiese
Universität Leipzig
Harald Wiese (Universität Leipzig)
Monopol und Monopson
1 / 53
Gliederung
Einführung
Haushaltstheorie
Unternehmenstheorie
Vollkommene Konkurrenz und Wohlfahrtstheorie
Marktformenlehre
Monopol und Monopson
Spieltheorie
Oligopoltheorie
Externe E¤ekte und ö¤entliche Güter
Pareto-optimaler Rückblick
Harald Wiese (Universität Leipzig)
Monopol und Monopson
2 / 53
De…nition: Monopol und Monopson
Monopol: ein Unternehmen als Verkäufer
Monopson: ein Unternehmen als Käufer
Monopol:
Preispolitik
Mengenpolitik
p
Π
X
Π
Harald Wiese (Universität Leipzig)
Monopol und Monopson
3 / 53
Preis- versus Mengenpolitik
p
II
I
Π (p )
Nachfrage
p
M
MR
Π
MC = AC
y
yM
Π (y )
III
IV
Π
Rum wie num!
Harald Wiese (Universität Leipzig)
Monopol und Monopson
4 / 53
Überblick
De…nition
Preispolitik im Monopol
Erlös und Grenzerlös bezüglich des Preises
Gewinn
Gewinnmaximierung (ohne Preisdi¤erenzierung)
Mengenpolitik im Monopol
Erlös und Grenzerlös bezüglich des Preises
Gewinn
Gewinnmaximierung ohne Preisdi¤erenzierung
Gewinnmaximierung mit Preisdi¤erenzierung
Mengen- und Gewinnsteuern
Wohlfahrtsanalyse
Monopson
Harald Wiese (Universität Leipzig)
Monopol und Monopson
5 / 53
Erlös und Grenzerlös bezüglich des Preises
Erlös für die Nachfragefunktion X (p ):
R (p ) = pX (p )
Grenzerlös (marginal revenue = MR, hier MRp ):
MRp =
dR
dX
= X +p
(Produktregel)
dp
dp
Wird der Preis um eine Einheit erhöht,
steigt der Erlös einerseits um X (für jede verkaufte Einheit
erhält das Unternehmen einen Euro)
sinkt der Erlös aber andererseits um p dX
dp (die Preiserhöhung
senkt die Nachfrage, die mit dem Preis bewertet wird)
Harald Wiese (Universität Leipzig)
Monopol und Monopson
6 / 53
Gewinn im linearen Modell
De…nition
X ist die Nachfragefunktion. Dann ist
Π (p ) : =
| {z }
R (p )
| {z }
Gewinn
Erlös
= pX (p )
C (p )
| {z }
Kosten
C [X (p )]
der Gewinn in Abhängigkeit vom Preis p und
Π (p ) = p (d
c, d, e
0, p
ep )
d
e
c ((d
ep )) ,
der Gewinn im linearen Modell.
Abhängigkeit: Preis 7! Menge 7! Kosten
Harald Wiese (Universität Leipzig)
Monopol und Monopson
7 / 53
Erlös, Kosten und eine Frage I
C, R
cd
C
R
p?
p?
p?
p?
p
Problem
Welche ökonomische Bedeutung haben die Preise mit Fragezeichen?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
8 / 53
Erlös, Kosten und eine Frage II
C, R
cd
C
R
p Π =0
Harald Wiese (Universität Leipzig)
p Rmax
p Π max
p X =C = R= Π =0
Monopol und Monopson
p
9 / 53
Grenzkosten bezüglich des Preises und bezüglich
der Menge
dC
dX
dC
dp
: Grenzkosten (bezüglich der Menge)
: Grenzkosten bezüglich des Preises
dC dX
dC
< 0.
=
dp
dX dp
|{z}
|{z}
>0
<0
Kettenregel: C (X (p )) ableiten nach p heiß
t:
zunächst nach X ableiten — > Grenzkosten
dann X weiter nach p ableiten — > Steigung der
Nachfragefunktion
von hinten interpretieren!
Harald Wiese (Universität Leipzig)
Monopol und Monopson
10 / 53
Gewinnmaximierung
Gewinnbedingung
dΠ !
dR
= 0 oder
dp
dp
dR ! dC
=
dp
dp
dC !
= 0 oder
dp
Diese Bedingung ist (wie wir später zeigen werden) gleichbedeutend
mit
dC
p dX
1
!
.
=
p
jεX ,p j
Problem
Bestätigen Sie: Der gewinnmaximale Preis im linearen Modell ist
ce
pM = d +
2e . Welcher Preis maximiert den Erlös?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
11 / 53
Gewinnmaximierung
komparative Statik
Wir haben
pM =
d + ce
2e
gefunden. Wie ändert sich pM , falls c steigt?
Ableiten:
dpM
1
=
dc
2
Harald Wiese (Universität Leipzig)
Monopol und Monopson
12 / 53
Übungen
Problem 1
Betrachten Sie einen Monopolisten mit der Kostenfunktion
C (X ) = cX , c > 0 und der Nachfragefunktion X (p ) = ap ε ,
ε < 1.
1
2
3
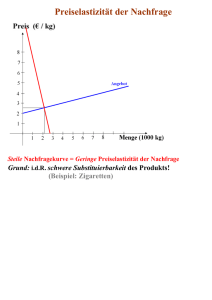
Bestimmen Sie die Preiselastizität der Nachfrage und den
Grenzerlös in Bezug auf den Preis!
Drücken Sie den Monopolpreis pM als eine Funktion von ε aus!
Bestimmen Sie und interpretieren Sie
dp M
d jεj
!
Problem 2
Die Nachfragefunktion sei gegeben durch X (p ) = 12 2p und die
Kostenfunktion des Monopolisten sei C (X ) = X 2 + 3. Bestimmen
Sie den gewinnmaximalen Preis!
Harald Wiese (Universität Leipzig)
Monopol und Monopson
13 / 53
Das lineare Modell
Erinnerung
p
a
p
a
R
1
a
2
b
p (X )
2b
1
MR
a
2b
Harald Wiese (Universität Leipzig)
ε X, p = 1
p(X )
MR
a
b
X
Monopol und Monopson
a
2b
a
b
X
14 / 53
Der Grenzerlös
Grenzerlös und Elastizität (Amoroso-Robinson-Relation)
dR
dp
= p+X
(Produktregel)
dX
dX
1
1
=p 1
> 0 für
= p 1+
εX ,p
jεX ,p j
MR =
Grenzerlös gleich Preis MR = p + X
horizontale (inverse) Nachfrage,
dp
dX
dp
dX
jεX ,p j > 1.
= p in drei Fällen:
= 0: MR = p + X
erste „kleine“ Einheit, X = 0: MR = p + X
=0
dp
dX
Preisdiskriminierung ersten Grades, MR = p + X
=0
=p=
dp
dX
=0
=p
R (X )
X
dp
dX
— > siehe unten
Harald Wiese (Universität Leipzig)
Monopol und Monopson
15 / 53
Der Gewinn
De…nition
Bei X
0 und der inversen Nachfragefunktion p ist
Π (X ) : = R (X )
| {z }
| {z }
Gewinn
Erlös
C (X ) = p (X ) X
| {z }
C (X )
Kosten
der Monopolgewinn in Abhängigkeit von der Menge.
Linearer Fall:
Π (X ) = (a
Harald Wiese (Universität Leipzig)
bX ) X
cX ,
Monopol und Monopson
X
a
b
16 / 53
Der Gewinn
Durchschnitts- und Grenzde…nition
p
Gewinn bei X̄ :
Π (X̄ )
= p (X̄ )X̄ C (X̄ )
= [p (X̄ ) AC (X̄ )] X̄
(Durchschnittsde…nition)
=
ZX̄
a
p(X )
G
E
F
c
[MR (X )
D
p (X )
MR
H
C
B
AC
MC
A
MC (X )] dX
X
X
0
F (gegebenenfalls)
(Grenzde…nition)
Harald Wiese (Universität Leipzig)
Monopol und Monopson
17 / 53
Mengenpolitik bei einheitlichem Preis
Gegeben:
Inverse Preis-Absatz-Funktion des Monopolisten: p = p (X )
Gesamtkosten: C (X )
Gewinn Π des Monopolisten:
Π (X ) = R (X ) C (X )
= p (X )X C (X ).
Notwendige Bedingung für das Gewinnmaximum:
dR
dΠ
=
dX
dX
bzw.
dC !
=0
dX
!
MR = MC
Harald Wiese (Universität Leipzig)
Monopol und Monopson
18 / 53
Mengenpolitik bei einheitlichem Preis
p
MC
AC
CournotPunkt
pM
Nachfrage
MR
XM
X
Problem
Inverse Nachfragefunktion p (X ) = 27 X 2 .
Erlösmaximaler und gewinnmaximaler Preis für MC = 15?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
19 / 53
Kluger Kopf:
Antoine Augustin Cournot
Antoine Augustin Cournot
(1801-1877) war ein französischer
Philosoph, Mathematiker und
Ökonom.
In seinem Hauptwerk „Recherches
sur les principes mathématiques de
la théorie des richesses“, 1838,
präsentiert Cournot wesentliche
Elemente der Monopoltheorie
(dieses Kapitel) und der
Oligopoltheorie (nächstes Kapitel).
Er…nder des Nash-Gleichgewichts
Harald Wiese (Universität Leipzig)
Monopol und Monopson
20 / 53
Mengenpolitik bei einheitlichem Preis
lineares Modell
p
a
pM
a
ε X ,p = 0
M
E
MC = AC
c
ε X ,p = 1
D
p(X )
p (X )
MR
c
p
ε X ,p = ∞
MR
A
F
B
XM
X PC
X M = X M (c, a, b) =
Harald Wiese (Universität Leipzig)
X
X
(
1 (a c )
2 b ,
0,
Monopol und Monopson
c a
c>a
21 / 53
Mengenpolitik bei einheitlichem Preis
der maximale Gewinn
p
MC
AC
CournotPunkt
pM
AC (X M )
Gewinn
Nachfrage
MR
XM
Harald Wiese (Universität Leipzig)
X
Monopol und Monopson
22 / 53
Mengenpolitik bei einheitlichem Preis
komparative Statik I
X M (a, b, c )
=
pM (a, b, c )
=
ΠM (a, b, c )
=
1 (a c )
2 b ,
wobei
1
2 (a + c ),
2
1 (a c )
,
4
b
wobei
wobei
∂X M
∂X M
∂c < 0; ∂a
∂p M
∂p M
∂c > 0; ∂a
∂ΠM
∂c
< 0;
∂ΠM
∂a
> 0;
> 0;
> 0;
∂X M
∂b
∂p M
∂b
< 0,
∂ΠM
∂b
= 0,
< 0.
Problem
(a c )2
Berechnen Sie ΠM (c ) = 14 b und auch
können die Kettenregel verwenden!
Harald Wiese (Universität Leipzig)
Monopol und Monopson
d ΠM
dc
! Hinweis: Sie
23 / 53
Mengenpolitik bei einheitlichem Preis
komparative Statik I
Solution
dΠM
dc
Harald Wiese (Universität Leipzig)
d
=
2
1 (a c )
4
b
dc
1
=
2( a c ) ( 1)
4b
a c
=
2b
Monopol und Monopson
24 / 53
Alternative Ausdrücke für die Gewinnmaximierung
1
!
MC = MR = p 1
1
!
p=
p
1
MC !
=
p
Harald Wiese (Universität Leipzig)
1
MC =
jεX ,p j
p
p 1
p
jεX ,p j
jεX ,p j
MC
jεX ,p j 1
1
jεX ,p j
Monopol und Monopson
=
1
jεX ,p j
25 / 53
Monopolmacht
vollkommene Konkurrenz:
Die Gewinnmaximierungsregel lautet „Preis = Grenzkosten“
Grund: Bei vollständiger Konkurrenz sind alle Unternehmen
„klein“ und haben keinen Ein‡uss auf den Preis. Die inverse
Nachfragekurve ist dann horizontal, also MR = p.
Monopol:
Der optimale Preis liegt im Allgemeinen oberhalb der
Grenzkosten.
De…nition (Lerner’scher Monopolgrad)
p
Harald Wiese (Universität Leipzig)
MC
p
Monopol und Monopson
26 / 53
Monopolmacht
Lerner’scher Monopolgrad
vollständige Konkurrenz: p = MC und daher
!
1
Monopol: MC = MR = p 1
p
MC ! p MR
=
=
p
p
=0
und daher
jεX ,p j
p
p MC
p
p 1
p
1
jεX ,p j
=
1
jεX ,p j
Interpretation: Wenn die Nachfrage stark auf Preiserhöhungen
reagiert, kann sich der Monopolist nur Preise nahe bei den
Grenzkosten leisten.
Harald Wiese (Universität Leipzig)
Monopol und Monopson
27 / 53
Monopolmacht, aber Monopolgewinn = null
p
Cournot-Punkt
pM
AC
MC
p (X )
MR
XM
X
p > MC aber AC X M
Harald Wiese (Universität Leipzig)
=
Monopol und Monopson
C XM
= pM
M
X
28 / 53
Formen der Preisdiskriminierung
Preisdiskriminierung ersten Grades:
Jeder Konsument bezahlt entsprechend seiner
Zahlungsbereitschaft.
=) vollständige Abschöpfung der Konsumentenrente
— > Kapitel „Mengenpolitik im Monopol“
Preisdiskriminierung zweiten Grades:
Für unterschiedliche Mengen werden unterschiedliche Preise
verlangt (z. B. Mengenrabatt).
=) Segmentierung der Kundschaft
Preisdiskriminierung dritten Grades:
Die Konsumenten werden in Gruppen eingeteilt.
=) Gleicher Preis nur innerhalb der Gruppe
Harald Wiese (Universität Leipzig)
Monopol und Monopson
29 / 53
Preisdiskriminierung ersten Grades
Jeder Konsument zahlt entsprechend seiner Zahlungsbereitschaft:
MR = p + X
=0
dp
=p
dX
Die Preissenkung infolge einer Mengenausdehnung betri¤t
nur den marginalen Konsumenten (den jeweils letzten
Konsumenten),
nicht jedoch die inframarginalen Konsumenten (diejenigen mit
höherer Zahlungsbereitschaft)
Harald Wiese (Universität Leipzig)
Monopol und Monopson
30 / 53
Preisdiskriminierung ersten Grades
Formal: Di¤erenzieren des Erlöses nach der Menge
Ry
d 0 p (q ) dq
MR =
= p (y )
dy
Hinweis: Ableitung eines Integrals nach der oberen Integrationsgrenze
ergibt den Wert des Integranden (hier p (q )) an der Stelle der oberen
Grenze.
Optimal:
!
p = MR = MC
Harald Wiese (Universität Leipzig)
Monopol und Monopson
31 / 53
Preisdiskriminierung ersten Grades
Grenzerlös
p
Produzentenrente
Grenzkosten
CournotPunkt
pM
p PC
Nachfrage =
Grenzerlös bei
Preisdiskriminierung
X M X PC
X
Grenzerlös ohne
Preisdiskriminierung
Problem
X (p ) = 12
1
2 p,
C (X ) = X 2 + 2
Harald Wiese (Universität Leipzig)
Monopol und Monopson
32 / 53
Preisdiskriminierung ersten Grades
Gewinnvergleich
p
a
pM
ε X ,p = ∞
ε X ,p = 1
D
p (X )
MR
c
A
ε X ,p = 0
M
E
B
XM
F
X PC
X
Gewinn für nicht diskriminierenden (Cournot) Monopolisten: ABME
= ABD
Gewinn für diskriminierenden Monopolisten: AFD
Harald Wiese (Universität Leipzig)
Monopol und Monopson
33 / 53
Preisdiskriminierung ersten Grades
Aufgabe
Ein Buchverkäufer kann ein Buch zu konstanten Grenzkosten von 8
herstellen (keine Fixkosten), und 11 potentielle Käufer haben
maximale Zahlungsbereitschaften von 55, 50, 45, ... , 10 und 5.
a) Keine Preisdiskriminierung:
Preis, Anzahl Bücher, Gewinn?
b) Preisdiskriminierung ersten Grades:
Preise, Anzahl Bücher, Gewinn?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
34 / 53
Preisdiskriminierung dritten Grades
zwei Märkte, eine Betriebsstätte I
Studenten, Rentner, Kinder, Tages- versus Nachtnachfrage
Gewinn
Π (x1 , x2 ) = p1 (x1 ) x1 + p2 (x2 ) x2
C (x1 + x2 ) ,
Maximierungsbedingungen
∂Π (x1 , x2 )
= MR1 (x1 )
∂x1
∂Π (x1 , x2 )
= MR2 (x2 )
∂x2
!
MC (x1 + x2 ) = 0,
!
MC (x1 + x2 ) = 0.
!
MR1 (x1 ) = MR2 (x2 )
Nehmen Sie an, dass im Gegensatz zur Gleichheit MR1 < MR2
gilt ...
Harald Wiese (Universität Leipzig)
Monopol und Monopson
35 / 53
Preisdiskriminierung dritten Grades
zwei Märkte, eine Betriebsstätte II
p
Markt 2
Markt 1
p1*
p2*
p2
x2
p1
x *2
x1*
MR2
x1
MR1
gesamte Absatzmenge
Harald Wiese (Universität Leipzig)
Monopol und Monopson
36 / 53
Preisdiskriminierung dritten Grades
zwei Märkte, eine Betriebsstätte III
MR1 (x1 ) = MR2 (x2 ) :
p1M 1
1
!
= p2M 1
j ε1 j
1
j ε2 j
jε1 j > jε2 j ) p1M < p2M .
also: inverse-Elastizitäten-Regel
Harald Wiese (Universität Leipzig)
Monopol und Monopson
37 / 53
Ein Markt, zwei Betriebsstätten
Gewinn:
Π (x1 , x2 ) = p (x1 + x2 ) (x1 + x2 )
C1 (x1 )
C2 (x2 )
Maximierungsbedingungen:
∂Π (x1 , x2 )
= MR (x1 + x2 )
∂x1
∂Π (x1 , x2 )
= MR (x1 + x2 )
∂x2
!
MC1 (x1 ) = 0
!
MC2 (x2 ) = 0
!
MC1 = MC2
Nehmen Sie an, dass im Gegensatz zur Gleichheit MC1 < MC2
gilt ...
Harald Wiese (Universität Leipzig)
Monopol und Monopson
38 / 53
Ein Markt, zwei Betriebsstätten
p
Betriebsstätte 2
Betriebsstätte 1
MC 2
x2
MC1
x *2
x1*
x1
gesamte Ausbringungsmenge
Harald Wiese (Universität Leipzig)
Monopol und Monopson
39 / 53
Übungen
Problem 1
Nehmen Sie an, dass Preisdi¤erenzierung nicht möglich ist.
Bestimmen Sie X M für p (X ) = 24 X und konstante Grenzkosten
c = 2! Bestimmen Sie zudem X M für p (X ) = X1 and konstante
Stückkosten c!
Problem 2
Auf dem ersten Teilmarkt gilt die inverse Nachfragefunktion
p1 = 12 4x1 , auf dem zweiten Teilmarkt die inverse
Nachfragefunktion p2 = 8 12 x2 . Die Grenzkosten betragen 4. Wie
hoch sind die Preise auf den Teilmärkten? Bestätigt sich die inverse
Elastizitätenregel?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
40 / 53
Mengen- und Gewinnsteuern
Mengensteuer
verteuert die Produktion für jede Einheit um den Steuersatz t
bewirkt eine Erhöhung der Grenzkosten MC auf MC + t
= a
!
2bX = MC + t
a MC t
) X M (t ) =
2b
) pM (t ) = a bX M (t )
a + MC + t
=
2
Die Steuer wird demnach zur Hälfte überwälzt.
MR
Problem
Skizzieren Sie!
Harald Wiese (Universität Leipzig)
Monopol und Monopson
41 / 53
Mengen- und Gewinnsteuern
Gewinnsteuer I
Ein Teil des Gewinns wird an den Staat abgeführt.
Ist dieser Teil (Prozentsatz), τ , konstant, bleibt anstelle des
Vorsteuergewinns R (X ) C (X ) nur der Nachsteuergewinn
(1
τ ) [R (X )
C (X )] .
=) keine Änderung der gewinnmaximalen Ausbringungsmenge als
Folge der Einführung einer Gewinnsteuer
Harald Wiese (Universität Leipzig)
Monopol und Monopson
42 / 53
Mengen- und Gewinnsteuern
Gewinnsteuer II
p
C (X )
R (X )
Π (X )
pM
MR
MC
(1 − t ) Π (X )
p (X )
XM
X
Mit dem Hammer auf das Gewinnmaximum schlagen ...
Harald Wiese (Universität Leipzig)
Monopol und Monopson
43 / 53
Das Monopol bei einheitlichem Preis
Wohlfahrtsverlust
Problem
p
MC
C
pM
pW
Wann ist die Summe aus
Konsumenten- und
Produzentenrente maximal?
A
R
Problem
T
Nachfrage
MR
yM
yW
Übergang C — > R
Pareto-Verbesserung?
y
Problem
D (q ) =
2q + 12, MC (q ) = 2q
Harald Wiese (Universität Leipzig)
Monopol und Monopson
44 / 53
Übungen
y (p ) = 8 12 p
MC = 4, keine Fixkosten
Mengensteuer t = 4
a) Preis, Konsumentenrente und Gewinn des Produzenten
vor der Steuererhebung?
b) Preis, Konsumentenrente und Gewinn des Produzenten
nach der Steuererhebung?
c) Steueraufkommen?
d) Wohlfahrtsverlust skizzieren!
Harald Wiese (Universität Leipzig)
Monopol und Monopson
45 / 53
Monopson
y = f (x1 , x2 ): Produktionsmenge bei der
Faktoreinsatzmengenkombination (x1 , x2 )
Der Gewinn beträgt
Π (x1 , x2 ) = p (f (x1 , x2 )) f (x1 , x2 )
{z
}
|
Erlös
(w (x ) x + w (x ) x ).
| 1 1 1 {z 2 2 2}
Kosten
Die notwendige Bedingung für ein Gewinnmaximum lautet:
dp ∂y
∂y
∂Π (x1 , x2 )
=
y + p (y )
∂x1
dy ∂x1
∂x1
dp
∂y
=
y + p (y )
dy
∂x1
= MR MP1 MC1
w1 (x1 ) +
dw1 (x1 )
x1
dx1
MC1
!
= Grenzerlösprodukt - Grenzkosten = 0.
Harald Wiese (Universität Leipzig)
Monopol und Monopson
46 / 53
Monopson
Notwendige Bedingungen für ein Gewinnmaximum:
!
MR1 = MC1
!
MR2 = MC2
Das Grenzerlösprodukt errechnet sich aus
MR1 =
dR ∂y
= MR MP1 .
dy ∂x1
Problem
Wie bestimmt man die Faktornachfragekurve im Monopsonfall?
Problem
Warum ist der Grenzerlös nicht gleich dem Preis (Nachfrageanalyse)?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
47 / 53
Monopson
Die Grenzkosten eines Faktors sind vom Faktorpreis verschieden.
Leitet man die Kosten für Faktor 1 nach der Anzahl der
Faktoreinheiten ab, erhält man die Grenzkosten von Faktor 1:
MC1 =
∂C
dw1
= w1 +
x1 .
∂x1
dx1
Problem
Wie lautet die Grenzkostenfunktion des Faktors Arbeit (A) bei
linearer inverser Faktorangebotsfunktion w (A) = a + bA?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
48 / 53
Monopson
w
Monopsonpreis
MC A
Arbeitsangebotskurve
w (A )
MR A
A
Kosten des Faktors Arbeit graphisch?
Ausbeutung?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
49 / 53
Monopson
Problem
Wie sollte man die Angebotselastizität der Arbeit de…nieren? Wie
hängen die Grenzkosten der Arbeit mit dieser Angebotselastizität
zusammen?
Also nochmal Amoroso-Robinson ...
Harald Wiese (Universität Leipzig)
Monopol und Monopson
50 / 53
Monopson
Gütermarkt
Faktormarkt
Optimalitätsbedingung für den Faktoreinsatz
MR1
=
dR ∂y
∂R
=
∂x1
dy ∂x1
MC1 =
= MR MP1
Spezialfall: Preisnehmer auf
dem Gütermarkt (MR = p )
Spezialfall: Preisnehmer auf
dem Faktormarkt
MR1 = p MP1 = MVP1
Harald Wiese (Universität Leipzig)
dw1
∂C
= w1 + x1
∂x1
dx1
Monopol und Monopson
dw1
dx1
=0
MC1 = w1
51 / 53
Zentrale Hörsaalübungen I
Aufgabe O.6.1.
C (y ) = 12 y 2 , p (y ) = 18
Cournot-Monopolmenge?
y
Aufgabe O.6.2.
y (p ) = 100 p
Zwei Betriebsstätten, y = y1 + y2 , mit
MC1 = y1 5 bzw.
MC2 = 21 y2 5
Optimale Produktionsmengen?
Aufgabe O.6.3.
Städtisches Schwimmbad mit x Besuchern
C (x ) = 1.500.000
Nachfrage Erwachsene: xE = 400.000 40.000pE
Nachfrage Kinder xK = 400.000 200.000pK
Harald Wiese (Universität Leipzig)
Monopol und Monopson
52 / 53
Zentrale Hörsaalübungen II
Aufgabe O.6.4.
C (y ) = y 2 + 2
D (p ) = 10 2p
Preisdiskriminierung ersten Grades
Aufgabe O.6.5.
Banana Co. einziger Arbeitgeber auf der Insel Banana
Inverse Angebotsfunktion für Arbeit: w (L) = 10 + L
Produktionsfunktion: f (L) = 10L
2 ist Weltmarktpreis für Bananen.
Wie viele Arbeiter stellt Banana Co. ein?
Arbeitslohn?
Harald Wiese (Universität Leipzig)
Monopol und Monopson
53 / 53