Wettbewerbspolitik und Regulierung

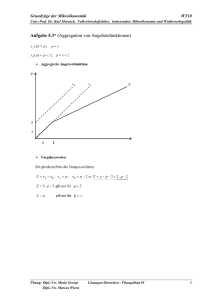
Lehrstuhl für Volkswirtschaftslehre
mit Schwerpunkt Ökonomie der Informationsgesellschaft
Lehrstuhlinhaber: Prof. Dr. Peter Welzel
Wettbewerbspolitik und Regulierung
Allgemeine Volkswirtschaftslehre für
Betriebswirte und Sozioökonomen
5. Semester
Skript
WS 2001/2002
Einführung und Kapitel 1
PD Dr. Karl Morasch
Wettbewerbspolitik und Regulierung
Vorbemerkungen, Einordnung und Aufbau
Inhaltsverzeichnis
Vorbemerkungen (zum Gesamtskript der Vorlesung)
iv
Inhaltliche Einordnung der Veranstaltung
v
Gliederung und Lernziele
vi
1 Analyse von Märkten mit unvollkommenem Wettbewerb
1
1.1 Marktmacht als Begründung für Wirtschaftspolitik
1
1.1.1 Vollständige Konkurrenz als Referenzmodell
2
1.1.2 Partialmarktanalyse: Pareto-Optimalität der Marktlösung
3
1.1.3 Allokatives Marktversagen aufgrund von Marktmacht
5
1.2 Modellierung des Oligopolwettbewerbs
7
1.2.1 Reaktionskurven und Cournot-Gleichgewicht
7
1.2.2 Stackelberg-Gleichgewicht
9
1.2.3 Kollusionslösung
10
1.2.4 Zahlenbeispiel: Mengenduopol mit linearer Nachfrage
11
1.2.5 Kartellinstabilität als „Gefangenendilemma“
13
1.3 Netzmärkte und natürliches Monopol
14
1.3.1 Natürliches Monopol beim Einproduktunternehmen
14
1.3.2 Mehrproduktunternehmen
16
1.4 Marktmacht und Wirtschaftspolitik – ein vorläufiges Fazit
- ii -
18
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Vorbemerkungen, Einordnung und Aufbau
Vorbemerkungen
Das vorliegende Skript zur Veranstaltung „Wettbewerbspolitik und Regulierung“ im
Wintersemester 2001/2002 soll Ihnen das Mitschreiben und die Nachbereitung der Veranstaltung erleichtern. Bitte beachten Sie: Die Lektüre des Skripts kann den Besuch
der Vorlesung nicht ersetzen! Prüfungsrelevant ist das, was in der Veranstaltung behandelt wird. Das Skript ist als Leitfaden gedacht, den Sie in der Vorlesung kommentieren und ergänzen sollten. Die Folien zur Veranstaltung sind entweder im Skript abgedruckt oder die entsprechende Information ist dem Text zu entnehmen (es wird dann
jeweils auf die zugehörige Folie hingewiesen). Die Übungsaufgaben zur Veranstaltung
sind im Skript nicht enthalten, sondern werden auf den Web-Seiten des Lehrstuhls bereitgestellt.
Das Skript umfaßt in der gegenwärtigen Form die Kapitel 1 und 2 der Veranstaltung,
sowie die Abschnitte 3.1 und 3.2 von Kapitel 3. Zu Abschnitt 3.3 „Regulierung in der
Praxis: Telekommunikation und Energieversorgung“ sei auf die Kapitel 4 und 5 in
Knieps, G., Brunekreeft, G. (2000), Zwischen Regulierung und Wettbewerb. Netzsektoren in Deutschland, Heidelberg: Physica verwiesen.
Das Skript ist auf Basis der Vorlesungsunterlagen und Skripten zur VorgängerVeranstaltung „Wirtschaftsordnungs- und Prozeßpolitik“ entstanden. An früheren Versionen dieser Unterlagen haben Tina Emslander, Hans-Helmut Bünning und Günter
Lang mitgewirkt. Günter Lang hat zudem bis WS 1996/97 diese Vorlesungsunterlagen
gepflegt und aktualisiert. Ohne diese Vorarbeit gäbe es das Skript in der gegenwärtigen
Form wohl nicht. Für verbleibende Mängel und Fehler bin ich jedoch allein verantwortlich. Es ist zu betonen, daß es sich um ein Skript und kein voll ausgearbeitetes Lehrbuch
handelt. So werden manche Dinge nur recht knapp angesprochen und erschließen sich
Ihnen darum vielleicht nur im Zusammenhang mit den Erläuterung in der Veranstaltung.
Zudem wird mit Quellenangaben recht nachlässig umgegangen. Für Kritik und Verbesserungsvorschläge wäre ich Ihnen dankbar.
Augsburg, im Oktober 2001
Karl Morasch
- iii -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Vorbemerkungen, Einordnung und Aufbau
Zur inhaltlichen Einordnung der Veranstaltung
Die Vorlesung „Wettbewerbspolitik und Regulierung“ schließt an die Veranstaltung
„Einführung in die Wirtschaftspolitik“ aus dem 4. Semester des Grundstudiums an. Sie
führt die dort angestellten Überlegungen zur Wirtschaftspolitik fort und wendet sie auf
zwei eng zusammenhängende Politikbereiche an, die in der einführenden Veranstaltung
nur am Rande thematisiert werden konnten. Während der Schwerpunkt im 4. Semester
auf der makroökonomischen Wirtschaftspolitik (Geld- und Fiskalpolitik) lag, bilden
Überlegungen aus dem Bereich der Mikroökonomie die Grundlage der vorliegenden
Veranstaltung.
• Der Unterschied zwischen den beiden Vorgehensweisen besteht insbesondere darin,
daß im Rahmen der Makroökonomie im allgemeinen auf Basis von Aggregaten
(Staat, Konsumenten, Produzenten) argumentiert wird, während im Rahmen der
Mikroökonomie die Wahlentscheidungen der einzelnen Wirtschaftseinheiten die
Grundlage bilden.
• Gegenstand der Mikroökonomie können dabei sowohl einzelne Märkte bzw.
Branchen (Partialanalyse) als auch die Volkswirtschaft als Ganzes (Totalanalyse Allgemeine Gleichgewichtstheorie) sein. Für die vorliegende Veranstaltung ist nur der
erste Aspekt von Bedeutung, während in der vom Lehrstuhl im Sommersemester angebotenen Hauptstudiumsveranstaltung „Internationale Wirtschaftsbeziehungen“
auch der zweite Ansatz eine wichtige Rolle spielt.
• Im Rahmen der mikroökonomischen Analyse stellen die Konzepte „Effizienz“ und
„Wohlfahrt“ die zentralen Zielkategorien dar, während im Rahmen der makroökonomischen Politik insbesondere die Ziele des Stabilitäts- und Wachstumsgesetzes von
Bedeutung sind.
• Bei mikroökonomischer Politik geht es normalerweise nicht um kurzfristige Aspekte
wie die Stabilisierung der Konjunktur, sondern um die langfristige Festlegung von
Rahmenbedingungen bzw. die langfristige Steuerung bestimmter Sektoren.
- iv -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Vorbemerkungen, Einordnung und Aufbau
Grobgliederung der Veranstaltung (vgl. Folie 1-1)
In Kapitel 1, „Analyse von Märkten mit unvollkommenem Wettbewerb“, wird zunächst
erläutert, warum Marktmacht eine Begründung für wirtschaftspolitische Interventionen
darstellt. Die Modellierung des Oligopolwettbewerbs und das Konzept des natürlichen
Monopols stellen die weiteren Themen dieses Grundlagenkapitels dar.
Kapitel 2 behandelt dann den Bereich „Wettbewerbspolitik“. Hauptziel der Wettbewerbspolitik ist es, den Marktmechansimus funktionsfähig zu erhalten — z.B. zu verhindern, daß durch Kartelle der Wettbewerb zwischen den Unternehmen eingeschränkt
wird. Es werden sowohl die grundlegenden wettbewerbspolitischen Konzepte als auch
die konkreten wettbewerbsrechtlichen Regelungen in Deutschland und der Europäischen Union vorgestellt.
Kapitel 3, „Regulierung“, beschäftigt sich mit Wirtschaftssektoren, bei denen insbesondere aufgrund des Vorliegens eines natürlichen Monopols davon ausgegangen wird, daß
durch wettbewerbspolitische Rahmensetzung allein noch kein zufriedenstellendes Ergebnis garantiert werden kann. Man greift deshalb auf staatliche Steuerung bzw. Regulierung zurück. Als prominente Beispiele werden dabei die Bereiche „leitungsgebundene
Energieversorgung“ und „Telekommunikation“ herangezogen.
Zentrale Lernziele (vgl. Folie 1-2)
•
Wie wird Wettbewerbspolitik und Regulierung begründet? Inwieweit sind diese
Begründungen aus Sicht der Wirtschaftswissenschaften stichhaltig?
•
Welche konkreten Maßnahmen werden in den beiden Politikbereichen ergriffen?
Sind diese Maßnahmen zur Erreichung der Ziele geeignet, oder gibt es andere, angemessenere Instrumente?
•
Wie kann man erklären, daß unangemessene Instrumente eingesetzt bzw. aus Sicht
der Gesamtwohlfahrt ungerechtfertigte politische Eingriffe vorgenommen werden?
•
Was sind die zentralen institutionellen Regelungen im Bereich der Wettbewerbspolitik und bei der Regulierung von Netzmärkten?
-v-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
1 Analyse von Märkten mit unvollkommenem Wettbewerb
Grobgliederung von Kapitel 1 (vgl. Folie 1-3)
•
In 1.1 wird erläutert, warum Marktmacht eine Begründung für wettbewerbspolitische und regulierende Eingriffe des Staates darstellen kann. Dazu wird mit
Hilfe der Konzepte Konsumentenrente und Produzentenrente das Ergebnis eine
Marktes bei vollkommenem Wettbewerb mit demjenigen eines unregulierten
Monopols verglichen.
•
Wettbewerbspolitik ist insbesondere auf Oligopolmärkte ausgerichtet. In 1.2 wird
darum die Modellierung des Oligopolwettbewerbs in Grundzügen dargestellt.
•
Bei Netzmärkten liegt häufig ein sogenanntes „natürliches Monopol“ vor. Dieses
Konzept, das eine wichtige Grundlage für die staatliche Regulierung bildet, wird in
1.3 vorgestellt.
1.1 Marktmacht als Begründung für Wirtschaftspolitik
In diesem Abschnitt wird die Begründung wirtschaftspolitischen Handelns im Bereich
der Wettbewerbspolitik und der Regulierung thematisiert. Der Analyse liegt der Gedanke
zugrunde, daß die meisten Staatseingriffe ihren Grund in Marktunvollkommenheiten
haben, d.h. im teilweisen Versagen der Marktkoordinierung, deren Effizienz durch staatliche Politik wiederhergestellt werden muß bzw. deren Unzulänglichkeiten kompensiert
werden sollen. Wirtschaftspolitik ist jedoch nicht nur deswegen notwendig, weil die Bedingungen optimaler Marktkoordination in der Praxis meist nur unvollständig erfüllt
sind: Ohne einen entsprechenden ordnungspolitischen Rahmen - u.a. durch eine geeignete Wettbewerbspolitik - ist die Funktion von Märkten grundsätzlich nicht gewährleistet.
Neben den Rahmenbedingungen, die für ein Funktionieren von Märkten unabdingbar
sind lassen sich prinzipiell drei Marktversagenstatbestände unterscheiden, mit denen
wirtschaftspolitische Eingriffe gerechtfertigt werden: Allokatives Marktversagen, distributives Marktversagen und konjunkturelles Marktversagen. Marktmacht ist eine Form
des allokativen Marktversagens - die anderen Formen dieses Marktversagenstatbestands
werden in Zusammenhang mit der Erläuterung des Referenzmodells der vollständigen
Konkurrenz kurz angesprochen. Grundidee ist dabei, daß einzelne Voraussetzungen der
vollständigen Konkurrenz nicht erfüllt sind und somit eine effiziente Allokation durch
den Marktmechanismus nicht mehr sichergestellt ist.
-1-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
1.1.1 Vollständige Konkurrenz als Referenzmodell
Es kann gezeigt werden, daß sich unter bestimmten Voraussetzungen durch den
Marktmechanismus ein pareto-optimaler Zustand ergibt (d.h. keine Person kann besser
gestellt werden ohne eine andere schlechter zu stellen). Abweichungen von den zentralen Voraussetzungen des Modells führen dazu, daß dieses Optimum durch die Marktlösung nicht mehr realisiert werden kann. Wie bereits angesprochen, stellt dieses sogenannte Marktversagen einen wichtigen Ansatzpunkt für Wirtschaftspolitik dar. Durch
geeignete wirtschaftspolitische Maßnahmen soll das Optimum erreicht oder zumindest
eine Annäherung an den effizienten Zustand erzielt werden. Referenzmodell für dieses
Marktversagen ist die Funktionsweise eines Marktes mit vollständiger Konkurrenz. Dazu
müssen die folgenden Bedingungen erfüllt sein:
•
Es existiert keine Marktmacht: Das Angebot auf dem Markt (für ein homogenes
Gut!) erfolgt durch eine Vielzahl von Unternehmen, für die der Marktpreis eine vorgegebene Größe ist - sie verhalten sich als Preisnehmer bzw. Mengenanpasser;
analog muß das Mengenanpasserverhalten auch für die Nachfrageseite gelten.
•
Beim betrachteten Gut handelt es sich um ein privates Gut, d.h. es liegt Rivalität im
Konsum vor und andere Konsumenten können vom Konsum des Gutes ausgeschlossen werden.
•
Es liegen keine externen Effekte beim Konsum oder der Produktion vor, d.h. alle
Nutzen bzw. Kosten, die sich bei der Produktion oder beim Konsum des Gutes ergeben, fallen ausschließlich bei den Produzenten bzw. den Konsumenten an.
•
Es besteht vollständige Information über alle Preise und die Qualität der Güter.
•
Güter- und Faktorpreise sind vollkommen flexibel, d.h. sie passen sich bei Angebots- bzw. Nachfrageänderungen ohne Verzögerung an.
Wird eine dieser Bedingungen verletzt, so spricht man von Marktversagen. Im Rahmen
dieser Veranstaltung beschränken wir uns weitgehend auf wirtschaftspolitische Interventionen, die aufgrund der ersten Form des Marktversagens (Marktmacht von Unternehmen) durchgeführt werden. Andere Formen werden Sie in anderen Vorlesungen
kennenlernen, z.B. öffentliche Güter oder externe Effekte im Rahmen finanzwissenschaftlicher oder umweltpolitischer Veranstaltungen.
-2-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
Im folgenden wird zunächst die Pareto-Optimalität der Marktlösung für einen Partialmarkt aufgezeigt. Dabei werden auch die Konzepte Konsumentenrente, Produzentenrente und sozialer Überschuß erläutert, die beim anschließenden Vergleich mit dem Ergebnis beim Monopol herangezogen werden.
1.1.2 Partialmarktanalyse: Pareto-Optimalität der Marktlösung
Die Volkswirtschaften der Industrieländer können durch die Dominanz marktwirtschaftlicher Organisationsprinzipien charakterisiert werden. Dies bedeutet, daß die Koordination einzelwirtschaftlicher Aktivitäten über Märkte erfolgt: Sich nach Angebot und
Nachfrage bildende Preise sorgen für Markträumung. Die Nachfrage in Abhängigkeit
vom Marktpreis ist dabei das Ergebnis der Nutzenmaximierung der privaten Haushalte,
während sich das Angebot in Abhängigkeit vom Marktpreis als Resultat der Gewinnmaximierung der Unternehmen einstellt. Wie Sie bereits im Grundstudium gelernt haben,
führt der Marktprozeß auf einem einzelnen Markt unter idealen Voraussetzungen zu
einer Maximierung des sozialen Überschusses, d.h. der Summe aus Konsumenten- und
Produzentenrente. Da die Analyse mit Hilfe dieser partialanalytischen Wohlfahrtsmaße
in der Veranstaltung eine wichtige Rolle spielt und die Effizienz von Märkten im Partialmodell besonders einfach dargestellt werden kann, sollen diese Aspekte hier nochmals kurz angesprochen werden.
Die Angebotskurve entspricht bei Preisnehmerverhalten der Unternehmen deren Grenzkostenkurve: Die Unternehmen sind bereit, eine zusätzliche Einheit anzubieten, solange
der Preis höher ist als die Grenzkosten. Analog steht hinter der Nachfragekurve der
Grenznutzen der Konsumenten: Der Konsum einer weiteren Einheit des Gutes ist vorteilhaft, wenn der dafür zu entrichtende Preis geringer ist, als der aus dem Konsum
resultierende zusätzliche (in Geldeinheiten bewertete) Nutzen. Das Marktgleichgewicht
auf einem Partialmarkt ergibt sich im Schnittpunkt von Angebot und Nachfrage. Da hier
der Grenznutzen der Konsumenten den Grenzkosten der Unternehmen entspricht, wird
der gesamtwirtschaftliche Überschuß maximiert. Dieses Ergebnis wird in Folie 1-4 graphisch mit Hilfe der Konzepte Konsumenten- und Produzentenrente verdeutlicht:
-3-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
Sozialer Überschuß
Statische Wohlfahrtsmessung auf isolierten Märkten
p
Konsumentenrente
A
Marktgleichgewicht
p*
N
Produzentenrente
x*
x’
x
# 1-4
Die Konsumentenrente läßt sich graphisch als Fläche zwischen Nachfragekurve und
Preisgerade darstellen. Da die Nachfragekurve zu jeder Mengeneinheit den entsprechenden in Geld ausgedrückten Grenznutzen angibt, stellt die Fläche unter der Nachfragekurve den resultierenden (Brutto-)Nutzen dar. Zieht man davon den Gesamtpreis für die
entsprechende Menge ab - graphisch ist das die Fläche unter der Preisgerade -, so erhält
man den Nettonutzen der Konsumenten, der sich bei dieser Preis-Mengen-Kombination
einstellt. Die Rente entsteht, weil alle Konsumenten einen einheitlichen Preis entrichten
müssen - also auch diejenigen, die eine höhere Zahlungsbereitschaft für das Gut haben.
Analog ist die Produzentenrente als Fläche zwischen Preisgerade und Grenzkosten bzw.
Nachfragekurve gegeben: Die Fläche unter der Preisgerade gibt den Umsatz an während
die Fläche unter der Grenzkostenkurve die Summe der (variablen) Stückkosten widerspiegelt. Im langfristigen Gleichgewicht bei vollkommenem Wettbewerb entspricht die
Produzentenrente gerade den Fixkosten, d.h. es treten keine ökonomischen Gewinne
oder Verluste auf. Die Summe aus Produzenten- und Konsumentenrente stellt das
Wohlfahrtsmaß „Sozialer Überschuß“ dar. Durch den Vergleich dieser Größe für verschiedene Situationen, läßt sich dann eine Aussage darüber treffen, welche davon unter
Wohlfahrtsaspekten vorzuziehen wäre. Der soziale Überschuß ist jedoch nur dann ein
sinnvoller Indikator, wenn die Fixkosten jeweils identisch sind - ansonsten ist es sinnvoller, statt der Produzentenrente die Gewinne zu berücksichtigen, d.h. die Summe aus
Gewinnen und Konsumentenrente als Wohlfahrtsmaß zu verwenden.
In der Abbildung in Folie 1-4 läßt sich nun unschwer erkennen, daß das Marktgleichgewicht den sozialen Überschuß maximiert: Ausgehend von einer Menge x < x* ist es
offensichtlich, daß eine Mengenausweitung die Summe aus Konsumenten- und Produzentenrente erhöht. Eine weitere Erhöhung der Menge über x* hinaus ist nicht vorteil-
-4-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
haft, wie das Beispiel x' zeigt: Die schraffierte Dreiecksfläche zwischen x* und x' stellt
einen Rückgang der Wohlfahrt dar, da hier die Angebotskurve über der Nachfragekurve
liegt und somit die Grenzkosten höher sind als der Grenznutzen.
Beachten Sie, daß die allokative Effizienz einzelner Märkte an der Maximierung des sozialen Überschusses, also der Summe aus Konsumenten- und Produzentenrente, gemessen wird. Die Verteilung des Wohlstandes auf die Marktteilnehmer, also die Aufteilung
des sozialen Überschusses nach Konsumenten und Produzenten, wird somit bei einer
rein allokativer Betrachtung nicht bewertet. Der Aspekt Verteilung ist eine separate wirtschaftspolitische Aufgabe - der Markt führt zwar zu einem effizienten, aber nicht notwendigerweise zu einem gerechten Ergebnis.
1.1.3 Allokatives Marktversagen aufgrund von Marktmacht
In der Realität gibt es viele Märkte mit unvollkommenem Wettbewerb, d.h. die Unternehmen können die Preise beeinflussen. Dies kann daran liegen, daß nur wenige Anbieter (Oligopol) vorhanden sind, oder daß differenzierte Produkte (monopolistische Konkurrenz) hergestellt werden. Der Extremfall unvollkommenen Wettbewerbs ist das Monopol, bei dem auf einem Markt nur ein einziges Unternehmen aktiv ist. Monopole können sich sowohl durch die Kostenstruktur (natürliches Monopol - näheres siehe unten),
als auch durch Markteintrittsbarrieren (z.B. Patente, staatliche Konzessionierung etc.)
ergeben. Im Monopolfall resultiert im Vergleich zum vollkommenen Wettbewerb eine
geringere Gütermenge, die zu einem höheren Preis abgesetzt wird. Wie in Folie 1-5
deutlich wird, kommt es durch Monopole gegenüber der Situation bei vollkommenem
Wettbewerb sowohl zu einer Umverteilung als auch zu einem Effizienzverlust.
Konsequenzen von Monopolen
Allokative und distributive Wirkungen
p
Umverteilung
zum Anbieter
pM
Effizienzverlust
("deadweight-loss")
pW
GK
N
xM
xW
GE
-5-
x
# 1-5
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
Dabei ist die Umverteilung von den Konsumenten zum Produzenten von geringerer Bedeutung: Theoretisch kann dieser Gewinn einfach durch eine Steuer abgeschöpft und
wieder den Konsumenten zugeleitet werden. Problematisch ist jedoch der Rückgang des
sozialen Überschusses, also die Entstehung allokativer Ineffizienz: Die Produktionsmenge des betrachteten Gutes sinkt unter die volkswirtschaftlich optimale Menge ab im Bereich zwischen xM und xW liegt die Zahlungsbereitschaft der Konsumenten über
den Grenzkosten des Monopolisten. Es entsteht ein sogenannter deadweight-loss, der
selbst bei vollständiger Abschöpfung des Monopolgewinns nicht vermieden werden
kann. Zumindest im einfachen Monopolmodell wird dieses (suboptimale) Outputniveau
jedoch auch durch einen Monopolisten technisch effizient produziert: Da er an einer
Maximierung seines Gewinnes interessiert ist, werden die Produktionsfaktoren optimal
eingesetzt. In der Realität zeigt sich jedoch häufig, daß bei Monopolen aufgrund fehlenden Wettbewerbsdrucks langfristig auch die Kosteneffizienz leidet („X-Ineffizienz“).
Im Rahmen der im dritten Kapitel diskutierten Regulierung spielen sogenannte „natürliche Monopole“ eine zentrale Rolle (z.B. bei der leitungsgebundenen Energieversorgung). In diesem Fall ist aufgrund der Kosten- und Nachfragestruktur die Produktion
durch ein einziges Unternehmen am kostengünstigsten. Die Existenz des Monopols muß
dann akzeptiert werden, durch staatliche Regulierung versucht man jedoch die negativen
Effizienzeffekte möglichst zu vermeiden. Das Konzept des natürlichen Monopols wird
in Abschnitt 1.3 noch ausführlich besprochen.
Oligopolmärkte ergeben sich ebenso wie Monopolmärkte häufig aufgrund der Kostenstruktur: Die mindestoptimale Betriebsgröße (Grenzkosten sinken nicht mehr) ist im
Verhältnis zur Nachfrage so groß, daß nur einige wenige Unternehmen kosteneffizient
produzieren können. Solche Oligopolmärkte sind dadurch gekennzeichnet, daß sich die
Unternehmen der zwischen ihnen bestehenden Interdependenz bewußt sind. In Oligopolmärkten (z.B. Kraftfahrzeugbau, Stahlindustrie) versucht der Staat durch Wettbewerbspolitik zu verhindern, daß die Oligopolisten durch Kartelle eine Quasi-Monopolstellung erlangen bzw. durch Fusionen einzelne Unternehmen mit zu großer Marktmacht
entstehen (genaueres in Kapitel 2). Wie Wettbewerb auf Oligopolmärkten funktioniert
wird im folgenden Abschnitt 1.2 erläutert.
Die Konzepte zur Analyse unvollkommenen Wettbewerbs sind relativ anspruchsvoll, so
daß ergänzend zu Vorlesung und Skript die Lektüre der folgenden beiden Literaturstellen empfohlen wird: Pindyck, R.S., Rubinfeld, D.L. (1989), Microeconomics, 427-43
zum Oligopolwettbewerb und Train, K.E. (1991), Optimal Regulation, 1-17 [alternativ:
Knieps. G. (2001), Wettbewerbsökonomie, 21-28] zum natürlichen Monopol.
-6-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
1.2 Modellierung des Oligopolwettbewerbs
Oligopolwettbewerb liegt vor, wenn auf einem Markt einige wenige Unternehmen miteinander in Wettbewerb stehen. Diese Situation tritt dann auf, wenn Markteintrittsbarrieren in irgendeiner Form bestehen, z.B. aufgrund von Skalenerträgen oder Patenten. Wie
beim Monopol verhalten sich die Oligopolisten nicht als Mengenanpasser, sondern sind
sich darüber im klaren, daß sie durch Ausweitung oder Einschränkung der eigenen Absatzmenge den Marktpreis beeinflussen. Bei der Analyse des Oligopolwettbewerbs ergeben sich jedoch zusätzliche Komplikationen: Die Aktionen eines Unternehmens wirken
sich auf die Gewinnsituation der Wettbewerber aus, und es ist davon auszugehen, daß
diese ihre Strategien entsprechend anpassen werden - wenn z.B. Opel die Automobilpreise um 5% senkt, so kann es nicht davon ausgehen, daß VW oder Ford ihre bisherige
Preispolitik unverändert beibehalten.
Um diese Situation oligopolistischer Interdependenz zu analysieren, werden wir im weiteren auf das sogenannte „Cournot-Modell“ zurückgreifen, wobei wir vom einfachsten
Fall, einem homogenen Mengen-Duopol ausgehen - d.h. von einem Oligopolmarkt mit
zwei Wettbewerbern die ein identisches Produkt herstellen und deren Entscheidungsproblem in der Festlegung der Absatzmenge besteht.1 Wie im Monopolfall nehmen wir
dabei an, daß beiden Unternehmen die Marktnachfragekurve bekannt ist. In einem ersten
Schritt wird dabei in 1.2.1 das Konzept der Reaktionskurve erläutert und das CournotGleichgewicht bei simultaner, nicht-kooperativer Festlegung der Menge ermittelt. Anschließend wird in 1.2.2 das Stackelberg-Gleichgewicht (sequentielle Wahl des Outputs)
und in 1.2.3 das Kollusionsgleichgewicht (kooperative Festlegung) bestimmt. Im Rahmen eines Zahlenbeispiels werden dann in 1.2.4 diese Resultate mit dem Monopol und
mit vollkommenem Wettbewerb verglichen. Schließlich erfolgt in 1.2.5 eine Analyse des
Problems der Kartellinstabilität.
1.2.1 Reaktionskurven und Cournot-Gleichgewicht
Die Entscheidungssituation der Unternehmen und die Bestimmung des Gleichgewichts
läßt sich im Duopolfall mit Hilfe sogenannter „Reaktionskurven“ in einer zweidimensionalen Abbildung darstellen (vgl. Folie 1-6). Die Reaktionskurven, die sich aus dem Gewinnmaximierungskalkül der Unternehmen ergeben, stellen einen Zusammenhang zwi-
1 Das
Cournot-Modell kann als reduzierte Form eines zweistufigen Spiels mit Kapazitätswettbewerb auf
der ersten und Preiswettbewerb auf der zweiten Stufe aufgefaßt werden (vgl. Kreps/Scheinkman, 1983).
Die formal komplizierteren Preisoligopole werden darum in der Veranstaltung nicht betrachtet.
-7-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
schen den Absatzmengen der beiden Wettbewerber her: Werden die Absatzmengen von
Unternehmen 1 bzw. 2 mit x1 bzw. x2 bezeichnet, so gibt die Reaktionsfunktion
x1 = R1(x2) an, welche Absatzmenge x1 den Gewinn von Unternehmen bei gegebenem
Output x2 des Wettbewerbers maximiert. Entsprechend liefert die Reaktionsfunktion
x2 = R2(x1) den zu gegebener Menge x1 gewinnmaximalen Output x2 des Duopolisten 2.
Bei einer Darstellung im (x1, x2)-Raum verlaufen die Reaktionskurven fallend, weil eine
Erhöhung der Absatzmenge durch ein Unternehmen zu einem geringeren Marktpreis
führt und damit die Gewinnmargen reduziert. Weiterhin folgt aus den Stabilitätsbedingungen (Konzept analog zur Stabilität des Marktgleichgewichts), daß die Reaktionskurve
von Unternehmen 1 steiler sein muß, als diejenige von Unternehmen 2.
x2
Cournot-Gleichgewicht
R 1(x 2)
Isogewinnkurven von U1
C
StackelbergGleichgewicht
S
R 2(x 1)
x1
# 1-6
Ebenfalls in die Abbildung eingezeichnet sind Isogewinnkurven aus der Isogewinnkurvenschar von Unternehmen 1. Diese Isogewinnkurven sind nach unten geöffnet,
verlaufen im Schnittpunkt mit der eigenen Reaktionskurve waagrecht - der Gewinn wird
ja dort zu gegebener Absatzmenge des anderen Unternehmens maximiert - und repräsentieren ein umso höheres Gewinnniveau, je tiefer sie liegen. Analog gilt für die Isogewinnkurven von Unternehmen 2: Sie sind nach links geöffnet, verlaufen im Schnittpunkt mit der eigenen Reaktionskurve senkrecht und repräsentieren ein umso höheres
Gewinnniveau, je weiter links sie liegen.
Im Schnittpunkt der beiden Reaktionskurven befindet sich das Cournot-Gleichgewicht
C. Wenn die Unternehmen gleichzeitig und unabhängig voneinander ihre Absatzmengen
festlegen, so stellt die Cournot-Menge die optimale Strategie für jedes Unternehmen dar.
In der Sprache der Spieltheorie handelt es sich um ein Nash-Gleichgewicht: Wenn das
andere Unternehmen die Cournot-Menge als Strategie wählt, so wird der eigene Gewinn
maximiert, wenn ebenfalls die Cournot-Menge abgesetzt wird (beide Unternehmen befinden sich ja auf ihrer Reaktionskurve). Bei simultaner Bestimmung der Strategien hat
im Cournot-Gleichgewicht keines der Unternehmen einen Anreiz von der gewählten
-8-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
Strategie abzuweichen: sie stellen wechselseitig beste Antworten dar. Sowohl aus Sicht
eines einzelnen Unternehmens als auch aus Sicht der Gesamtbranche existieren jedoch
andere Outputkombinationen, die zu höheren Gewinnen für das einzelne Unternehmen
bzw. für die Branche führen würden. Unter welchen Umständen sich diese alternativen
Lösungen realisieren lassen, wird in 1.2.2 und 1.2.3 thematisiert.
1.2.2 Stackelberg-Gleichgewicht
Für ein einzelnes Unternehmen ist ein höherer Gewinn als im Cournot-Gleichgewicht
erreichbar, wenn es sich zeitlich vor seinem Wettbewerber unwiderruflich auf eine Absatzmenge festlegen kann und diese Festlegung dem Wettbewerber bekannt ist. Im Reaktionskurvendiagramm läßt sich das sogenannte Stackelberg-Gleichgewicht folgendermaßen darstellen: Unternehmen 1 - der Stackelberg-Führer - bestimmt zu gegebenem
Optimalverhalten seines Konkurrenten, d.h. auf dessen Reaktionskurve R2(x1), diejenige
Absatzmengenkombination (x1, x2), bei der es den höchsten Gewinn erzielt. Unter Verwendung der zuvor eingeführten Isogewinnkurven läßt sich diese Mengenkombination
als Tangentialpunkt S zwischen einer Isogewinnkurve von Unternehmen 1 und der Reaktionskurve R 2(x1) identifizieren (siehe oben Folie 1-6).
Gegenüber dem Cournot-Gleichgewicht weitet Unternehmen 1 seine Absatzmenge aus,
während Unternehmen 2 die Absatzmenge einschränkt. Es läßt sich zeigen, daß sich die
Gesamtmenge x1 + x2 erhöht, wodurch sich aufgrund des sinkenden Marktpreises letztendlich die Gewinnmarge verringert. Der Gewinn von Unternehmen 1 erhöht sich, während der Gewinn von Unternehmen 2 gegenüber dem Cournot-Gleichgewicht sinkt. Der
Gewinnzuwachs für Unternehmen 1 erfolgt somit auf Kosten des Wettbewerbers.
Es sei an dieser Stelle darauf hingewiesen, daß Unternehmen 1 nur dann die Position des
Stackelberg-Führers einnehmen kann, wenn es seinem Konkurrenten glaubhaft signalisiert, daß es die zum Punkt S gehörende Menge x1 produzieren wird. Eine bloße Ankündigung, ausgehend von Punkt C die Menge x1 entsprechend auszuweiten, genügt dieser
Anforderung nicht und führt für sich genommen zu keiner Bewegung weg vom Cournot-Gleichgewicht. Vielmehr bedarf es einer (Selbst-)bindung des Duopolisten 1, die
glaubhaft macht, daß es zukünftig im Interesse des Unternehmens ist, die zu S gehörende Menge zu produzieren. Eine Möglichkeit dafür bieten irreversible Investitionen, die
im anschließenden Outputspiel eine höhere Absatzmenge attraktiv machen. Alternativ
kann durch vertragliche Bindungen oder im Rahmen eines internationalen Duopols
durch Subventionen der inländischen Regierung an das inländische Unternehmen das
Stackelberg-Ergebnis realisiert werden.
-9-
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
1.2.3 Kollusionslösung
Sowohl das Cournot-Gleichgewicht als auch das Stackelberg-Gleichgewicht ist für die
Duopolisten suboptimal in dem Sinn, daß es ihnen aufgrund ihrer nicht miteinander abgestimmten Outputentscheidungen nicht gelingt, ihren gemeinsamen, d.h. aggregierten
Gewinn zu maximieren. Nimmt man nun zur Bestimmung der sogenannten Kollusionslösung an, daß die beiden Unternehmen ihre Absatzmengen gemeinsam festlegen,
dann führt dies zur Maximierung des aggregierten Gewinns. Jeder Duopolist berücksichtigt jetzt die negative Auswirkung einer Ausweitung der eigenen Absatzmenge auf den
Gewinn des anderen Unternehmens: Bei einer solchen Ausweitung der Menge sinkt der
Marktpreis und die Gewinnmarge für beide Unternehmen. Eine Berücksichtigung der
damit verbundenen Gewinneinbuße beim Konkurrenten führt dazu, daß die Unternehmen bei koordinierten Produktionsentscheidungen geringere Absatzmengen wählen als
im Cournot-Gleichgewicht. Folie 1-7 zeigt die Kollusionslösung graphisch:
x2
R1 (x 2 )
Kontraktkurve
Isogewinnkurven von U
C
2
Isogewinnkurven von U
1
K
R2 (x1 )
x1
# 1-7
Ein Berührpunkt zwischen einer Isogewinnkurven des Duopolisten 1 und einer Isogewinnkurve des Duopolisten 2 stellt eine pareto-optimale Absatzmengenkombination
dar: Es ist ausgehend von einem solchen Punkt nicht möglich, eines der beiden Unternehmen besserzustellen, ohne gleichzeitig den Gewinn des anderen zu reduzieren. Dies
bedeutet aber auch, daß der aggregierte Gewinn maximiert ist. Die Menge dieser paretooptimalen Tangentialpunkte wird auch als „Kontraktkurve“ bezeichnet; sie liegt unterhalb der beiden Reaktionskurven (die beiden Enden sind die jeweiligen Monopolmengen der Unternehmen). Auf dem Liniensegment zwischen den Isogewinnkurven der
beiden Unternehmen, die durch das Cournot-Gleichgewicht verlaufen, finden sich speziell jene Pareto-Optima, die gegenüber dem Cournot-Gleichgewicht C pareto-überlegen
sind. Bei symmetrischen Unternehmen scheint es plausibel, daß sich die beiden Unternehmen den Gesamtabsatz teilen; dies führt auf den Kollusionspunkt K. Für alle Punkte
auf der Kontraktkurve gilt, daß die Branchenproduktion im Kollusionsgleichgewicht
niedriger ist als im Cournot-Gleichgewicht. Der den Duopolisten aus der gemeinsamen
Gewinnmaximierung erwachsene Vorteil geht demnach zu Lasten der Konsumenten.
- 10 -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
1.2.4 Zahlenbeispiel: Mengenduopol mit linearer Nachfrage
Die bisher angeführten Überlegungen werden nun an einem Zahlenbeispiel verdeutlicht.
Dies soll einerseits helfen, die Gleichgewichtskonzepte zu verstehen, zum anderen sollen
die Ergebnisse bei Cournot-Wettbewerb mit dem Stackelberg-Gleichgewicht, der Kollusionslösung und dem Gleichgewicht bei vollkommenem Wettbewerb verglichen werden.
Wir gehen von einer linearen (inversen) Nachfragekurve p( X ) = α − β X mit α = 30
und β = 1 aus (d.h. p = 30 − X ), wobei X = x1 + x 2 die gesamte Absatzmenge beider
Unternehmen bezeichnet. Der Einfachheit halber nehmen wir an, daß die Kosten für
beide Unternehmen gleich null sind.2 In Folie 1-8 sind die resultierenden Reaktionskurven, die Kontraktkurve und die Gleichgewichte graphisch dargestellt; im folgenden
werden die Ergebnisse analytisch abgeleitet.
x2
30
R 1(x 2)
Kontraktkurve
W
15
10
7,5
Isogewinnkurve von U1
C
K
S
R2(x 1)
7,5 10
15
30
x1
# 1-8
Zur Bestimmung der Reaktionsfunktionen ermitteln wir zunächst die Bedingungen erster
Ordnung für die Gewinnmaximierung (Grenzertrag = Grenzkosten). Dies führt bei Unternehmen 1 ausgehend von der Gewinnfunktion π1 = px1 = [30 − ( x1 + x 2 )] x1 durch Ableiten nach x1 auf 30 − 2 x1 − x 2 = 0 . Wird die Ableitung nach x1 aufgelöst, so erhält man
die Reaktionsfunktion x1 = R 1( x 2 ) = 15 − 1 2 x 2 - diese Funktion gibt an, welche Absatzmenge x1 den Gewinn von Unternehmen 1 maximiert, wenn der Absatz von Unternehmen 2 gerade x2 beträgt. Das Cournot-Gleichgewicht kann man bestimmen, indem man
die beiden Bedingungen erster Ordnung der beiden Unternehmen simultan nach x1 und
x2 löst; dies führt auf x1 = x2 = 10. Der Gewinn eines Unternehmens beträgt dann 100.
2
Die Berücksichtigung von Fixkosten hätte keinen Einfluß auf die Gleichgewichte – nur die Gewinne der
Unternehmen würden reduziert. Identische und konstante variable Kosten c > 0 würden die qualitativen
Ergebnisse nicht verändern; wenn im gleichen Zug α auf α + c erhöht wird, erhielte man sogar exakt die
gleichen Lösungen. Erst asymmetrische variable Kosten c1 ≠ c2 haben einen nennenswerten Effekt: Der
Marktanteil des effizienteren Unternehmens übersteigt dann denjenigen seines Konkurrenten.
- 11 -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
Wenn die beiden Unternehmen den gemeinsamen Gewinn maximieren (Kollusion, d.h.
sie verhalten sich gemeinsam wie ein Monopolist), so werden sie geringere Absatzmengen wählen. Der gemeinsame Gewinn beträgt Π = π1 + π 2 = (30 − X ) X und die
Bedingung erster Ordnung für die Gewinnmaximierung lautet 30 − 2 X = 0 . Dies führt
auf einen Gesamtabsatz in Höhe von 15; die Kontraktkurve gibt alle möglichen Kombinationen x1 + x2 = 15 an und der Kollusionspunkt K die gleichmäßige Aufteilung
x1 = x2 = 7,5. Der Gewinn eines Unternehmens beläuft sich somit auf 112,5.
Bei vollkommenem Wettbewerb bestimmen die Unternehmen ihre Absatzmenge gemäß
der Regel Preis = Grenzkosten. Im vorliegenden Beispiel betragen die Grenzkosten null;
somit müßten die Unternehmen ihre Absatzmengen solange ausdehnen, bis der Preis auf
null sinkt. Die symmetrische Lösung lautet dann x1 = x2 = 15. Beim Oligopolwettbewerb
ergibt sich also eine geringere Menge als bei vollständiger Konkurrenz. In Kapitel 2
(Wettbewerbspolitik) wird gezeigt, daß der „Abstand“ zum Idealfall umso größer ist, je
weniger Unternehmen in einem Markt aktiv sind - diese Überlegung bietet eine Begründung für die Fusionskontrolle.
Kann Unternehmen 1 seine Absatzmenge zeitlich vor der Absatzentscheidung von Unternehmen 2 festlegen, so befindet es sich in der Position eines Stackelberg-Führers.
Unternehmen 2 wird in diesem Fall seine Absatzentscheidung zu gegebenem x1 gemäß
seiner Reaktionsfunktion x 2 = R 2 ( x1 ) = 15 − 1 2 x1 bestimmen. Unternehmen 1 berücksichtigt dies, indem es bei der Bestimmung der eigenen Absatzmenge die Auswirkung
auf die Absatzentscheidung des Wettbewerbers miteinkalkuliert. Formal wird dies erreicht, indem in der Gewinnfunktion von Unternehmen 1 statt x2 die Reaktionsfunktion
R2(x1) eingesetzt wird: π 1= [30 − x1 − (15 − 12 x1 )] x1 = 15x1 − 12 x12 . Die Maximierung
dieser Zielfunktion führt auf x1 = 15 und Einsetzen in die Reaktionsfunktion von Unternehmen 2 auf x2 = 7,5. Der Gewinn des Stackelberg-Führers beträgt dann 112,5; der des
anderen Unternehmens 56,25.
- 12 -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
1.2.5 Kartellinstabilität als „Gefangenendilemma“
Die Kollusionslösung maximiert zwar den gemeinsamen Gewinn der Unternehmen,
jedes einzelne Unternehmen hat jedoch einen Anreiz, von der im Rahmen eines Kartells
vereinbarten Mengen-Strategie abzuweichen: Wenn davon ausgegangen wird, daß das
andere Unternehmen sich entsprechend der Abmachung verhält, so ist es optimal, die
eigenen Absatzmenge gemäß der eigenen Reaktionskurve festzulegen - damit wird ja zu
gegebener Absatzmenge des Konkurrenten der eigene Gewinn maximiert (vgl. Pfeil in
Folie 1-8). In der Auszahlungsmatrix in Folie 1-9 werden die Gewinne der Unternehmen in Abhängigkeit der Strategien „Einhalten der Abmachung“ und „optimale Abweichung von der vereinbarten Mengenstrategie“ dargestellt:
Kartellinstabilität
"Abweichen" als dominante Strategie
Unternehmen 2
Unternehmen 1
einhalten
abweichen
einhalten
(113; 113)
(84; 127)
abweichen
(127; 84)
(84; 84)
Gewinn U1
Gewinn U2 (jeweils gerundet)
# 1-9
Wenn Kartellvereinbarungen nicht einklagbar sind, so läßt sich Kollusion im Rahmen
eines einperiodigen Simultanspiels nicht durchsetzen: Für beide Unternehmen stellt
„abweichen“ eine dominante Strategie dar, d.h. unabhängig davon ob der Partner die
Vereinbarung einhält oder nicht ergeben sich bei „abweichen“ höhere Auszahlungen
(Gewinne) als bei „einhalten“.
Dieses für die Unternehmen unangenehme Ergebnis ist natürlich aus Sicht der Wettbewerbspolitik erwünscht: Bei Kollusion würden die Unternehmen weniger anbieten als im
Cournot-Gleichgewicht, und das Marktergebnis würde sich noch weiter vom Idealfall
bei vollkommenem Wettbewerb entfernen. Vor diesem Hintergrund ist das Kartellverbot
im deutschen und europäischen Wettbewerbsrecht verständlich. Eine eingehende Analyse der Kartellproblematik, bei der auch dynamische Aspekte berücksichtigt werden,
erfolgt in Kapitel 2 im Rahmen der Analyse der Wettbewerbspolitik.
- 13 -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
1.3 Netzmärkte und natürliches Monopol
Die Existenz eines natürlichen Monopols stellt bei gleichzeitig vorliegenden Markteintrittsbarrieren in Form von sunk costs eine theoretisch überzeugende Begründung für
regulierende Eingriffe des Staates dar. Die Entstehung von Marktmacht ist hier eine
Konsequenz von gegebener Produktionstechnologie und Nachfrageeigenschaften.
Natürliche Monopole treten insbesondere in Netzmärkten - z.B. bei der leitungsgebundenen Energieversorgung - auf. Das Konzept wird zunächst anhand des Einproduktunternehmens erläutert; anschließend wird der in der Praxis häufigere Fall des Mehrproduktunternehmens betrachtet.
1.3.1 Natürliches Monopol beim Einproduktunternehmen
Zunächst sei das (Standard-)Beispiel eines Unternehmens herangezogen, das mit Hilfe
mehrerer Inputfaktoren lediglich ein einziges Gut produziere. Die Bedingungen für das
Vorliegen eines natürliches Monopols können dann wie folgt charakterisiert werden (vgl.
Folie 1-10):
Definition
Es ist am kostengünstigsten, wenn der ganze Markt
von einem einzigen Unternehmen versorgt wird.
Die Kostenfunktion ist strikt subadditiv.
n
K(x) < Σ Ki(xi)
i=1
n
mit x = Σ xi
i=1
Zentrale Ursache
Existenz von Skalenvorteilen
("Economies of Scale", Größenvorteile)
# 1-10
Größenvorteile der Produktion („economies of scale“) implizieren unter den Durchschnittskosten liegende Grenzkosten, so daß eine weitere Outputerhöhung die Durchschnittskosten absenkt. Wie die beiden Graphiken in Folie 1-11 zeigen, ist es dafür jedoch nicht notwendig, daß die Grenzkosten fallen (sinkende Grenzkosten führen demgegenüber immer zu sinkenden Durchschnittskosten). In beiden Fällen liegt ein natürliches Monopol vor. In der rechten Abbildung mit steigenden Grenzkosten ist diese Aussage jedoch von der Lage der Nachfragekurve abhängig: Bei deutlich höherer Nachfrage
kann die gewünschte Menge von mehr als einem Unternehmen kostengünstiger hergestellt werden.
- 14 -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
p,K
Analyse des unvollkommenen Wettbewerbs
p,K
N
N
GK
DK
DK
GK
x
x
# 1-11
Solche Größenvorteile der Produktion ergeben sich in der Realität häufig aufgrund der
Fixkostendegression des Kapitalstocks oder - in dynamischer Betrachtung - aufgrund
von Lernkurveneffekten.
Ein natürliches Monopol kann jedoch auch dann noch vorliegen, wenn keine steigenden
Skalenerträge (d.h. fallende Durchschnittskosten) mehr gegeben sind. Das natürliche
Monopols resultiert dann aus einer Unteilbarkeitssituation: Die Marktnachfrage ist
gerade so groß, daß die Größenvorteile eines Unternehmens vollständig ausgeschöpft
werden, jedoch nicht groß genug, damit zwei Unternehmen zu geringeren
Durchschnittskosten produzieren können. Eine solche Situation zeigt Folie 1-12:
p,K
DK
N
DK (xM /2)
DK (x M)
DKMin
xM/2
x*
Economies
of Scale
xM
Diseconomies
of Scale
x
# 1-12
Die Kostenfunktion ist hier zumindest bis zur Produktionsmenge xM subadditiv, obwohl
die Durchschnittskosten ab dem Outputniveau x* bereits wieder ansteigen: Die Durchschnittskosten DK(xM/2) bei Produktion durch zwei Unternehmen liegen über DK(xM).
Die Abbildungen in den Folien 1-12 und 1-13 verdeutlichen, daß die Lage der Nachfragekurve eine wichtige Rolle spielt. Zum einen führt in Folie 1-12 eine starke Rechtsverlagerung (Nachfragewachstum) dazu, daß kein natürliches Monopol mehr vorliegt (ähnlich wirkt eine Linksverschiebung der Durchschnittskostenkurve, z.B. aufgrund von
technologischem Fortschritt) – eine solche Entwicklung dürfte im Telekommunikationsbereich vorliegen. Zum anderen kann die Nachfragekurve jedoch auch so liegen, daß
trotz der Monopolpreise kein Gewinn entsteht (Folie 1-13, linke Abbildung), sondern
- 15 -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
das Unternehmen mit Verlust arbeiten würde – ein Beispiel hierfür ist der öffentliche
Personennahverkehr. In diesem Fall wird das Gut nur dann hergestellt, wenn der Staat
den Monopolisten mindestens in Höhe der entstehenden Verluste subventioniert. Der
Subventionsbetrag ist hier am geringsten, wenn es nur einen Anbieter gibt.
p,K
p,K
Gewinn
Verlust
M
pM
M
pM
DK
DK
GK
W
W
N
xM
GK
N*
x
xM
GE
x
GE*
# 1-13
Für die Wirtschaftspolitik gilt es zu prüfen, ob die Subvention sinnvoll ist. Dies ist
- partialanalytisch betrachtet - nur dann der Fall, wenn die erzielbare Konsumentenrente
bei der Preismengenkombination (pM, xM) größer ist als der notwendige Subventionsbetrag (entspricht der Verlustfläche in der Abbildung). Eine andere Möglichkeit bestünde in der Zulassung von Preisdiskriminierung, z.B. durch eine Grundgebühr zur Abschöpfung der Konsumentenrente und eine zusätzliche Nutzungsgebühr. Derartige
Preismodelle sind in der Elektrizitätswirtschaft anzutreffen.
1.3.2 Mehrproduktunternehmen
In der Realität produzieren Unternehmen häufig gleichzeitig mehr als ein einziges Gut.
Die Berücksichtigung solcher Mehrproduktunternehmen in der volkswirtschaftlichen
Theorie ist noch relativ neu. Das natürliche Monopol kann im Mehrproduktfall wie folgt
charakterisiert werden:
Definition
Eine spezifische Güterkombination kann am kostengünstigsten
von einem einzigen Unternehmen produziert werden.
Die Kostenfunktion ist strikt und global subadditiv.
K(x) + K(y) > K(x + y)
Zentrale Ursache
Economies of scope (Verbundvorteile)
# 1-14
Die Outputvektoren x und y stehen dabei für beliebige Mengen und Kombinationen der
betrachteten Güter. Beispielsweise kann der Outputvektor x sich auf Personennah- und
Fernverkehr, d.h. x = (xNah, xFern), und der Vektor y sich auf die Menge an Güterverkehr,
- 16 -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
d.h. y = yGüter, beziehen. Globale Subadditivität liegt dann vor, wenn für jede beliebige
Güter- und Mengenkombination die Produktion innerhalb eines Unternehmens kostengünstiger ist. So muß bei globaler Subadditivität für gegebene Mengen z.B. nicht nur
gelten, daß K( x, y ) < K( x ) + K( y ) , sondern auch K( x, y ) < K( x Nah ) + K( x Fern , y Güter )
und K( x, y ) < K( x Nah ) + K( x Fern ) + K( y Güter ) .
Die Subadditivität der Kostenfunktion im Mehrproduktfall ergibt sich insbesondere aus
der Komplementarität in der Produktion mehrerer Güter („economies of scope“ oder
Verbundvorteile). Solche Verbundvorteile liegen dann vor, wenn das Herausbrechen
einer bestimmten Produktlinie, d.h. Produktion in zwei Unternehmen statt in einem, die
Kosten der Gesamtproduktion erhöhen würde. Economies of scope ergeben sich häufig
aufgrund eines gemeinsam genutzten Fixkostenblocks, können aber auch aus der gemeinsamen Nutzung von Inputfaktoren resultieren, die zu den variablen Kostenbestandteilen zählen.
Ein Beispiel für den ersten Fall ist der Schienenverkehr. Durch eine Investition in Gleisanlagen ist das entsprechende Unternehmen in der Lage, gleichzeitig zwei verschiedene
Dienstleistungen anzubieten: Personenverkehr und Güterverkehr. Damit existiert ein
Kostenvorteil gegenüber der Alternativsituation, daß zwei verschiedene Anbieter diesen
Kapitalstock erstellen und jeweils nur Personen- bzw. Güterverkehr anbieten. Ein gegebener Fixkostenblock kann hier zur Produktion mehrerer Güter verwendet werden und
senkt somit die Durchschnittskosten. In diesem Zusammenhang sollte jedoch bedacht
werden, daß auch eine Aufteilung auf drei Unternehmen möglich wäre: Ein Anbieter der
Gleisanlagen könnte diese an das Personen- und das Güterverkehrsunternehmen vermieten. Somit liegt nur im Bereich des Schienennetzes tatsächlich ein natürliches Monopol vor. Im Sinne eines disaggregierten Regulierungsansatzes, wie er beispielsweise in
Knieps (2001) vertreten wird, sollte dann auch nur dieser „monopolistische Bottleneck“
einer staatlichen Regulierung unterworfen werden (genaueres dazu in Kapitel 3).
Verbundvorteile aufgrund von Kosteneinsparungen bei variablen Kostenbestandteilen
nennt man „Kuppelproduktion“. Dabei entstehen bei einem Produktionsvorgang gleichzeitig mehrere Produkte. Ein Beispiel dafür ist die gleichzeitige Produktion von Wärme
und Elektrizität durch Kraft-Wärme-Kopplung. Bei dieser hauptsächlich in den Kraftwerken der Industrie eingesetzten Technologie erhöht sich die Umwandlungseffizienz
beträchtlich, da der variable Kostenfaktor Primärenergie (z.B. Kohle) dann in geringeren
Mengen eingesetzt wird, als bei getrennter Produktion von Wärme und Strom. Ein anderes wichtiges Beispiel ist die Großchemie, die eine Vielzahl von Produkten in räumlich
benachbarten Anlagen erzeugt, um entsprechende economies of scope zu realisieren.
- 17 -
© K. Morasch, 2001
Wettbewerbspolitik und Regulierung
Analyse des unvollkommenen Wettbewerbs
1.4 Marktmacht und Wirtschaftspolitik – ein vorläufiges Fazit
Als vorläufiges Fazit zum Thema „Marktmacht als Begründung für Wirtschaftspolitik“
läßt sich ausgehend von den Überlegungen in Kapitel 1 folgendes festhalten:
• Das Grundproblem besteht in einem Spannungsverhältnis zwischen Produktionseffizienz (ein/wenige Anbieter am kostengünstigsten) und allokativer Effizienz.
• Beim natürlichen Monopol lautet der Lösungsansatz, die Monopolstellung aus
Kostengründen zuzulassen, den Monopolisten jedoch geeignet zu regulieren. Die dabei zum Einsatz kommenden Regulierungskonzepte werden in Kapitel 3 ausführlich
diskutiert
• Auf Oligopolmärkten sind die negativen Allokationswirkungen weniger stark ausgeprägt. Die in Kapitel 2 thematisierte Wettbewerbspolitik beschränkt sich deswegen
darauf, im Rahmen der Fusionskontrolle einer Verstärkung der Marktmacht entgegenzuwirken, den Mißbrauch besthender Marktmacht zu verhindern und durch das
Kartellverbot kollusives Verhalten zu unterbinden.
- 18 -
© K. Morasch, 2001