1 Zur Vorbereitung
Werbung

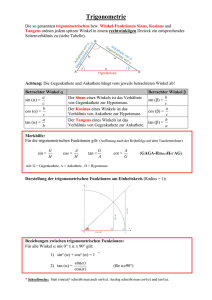
Labor zur Vorlesung Technische Optik Versuch 7: Polarisationsmodulation 1 Zur Vorbereitung Sie sollten mit den folgenden Begriffen umgehen können: Polarisation, linear und zirkular polarisiertes Licht, Faraday-Effekt, 2 Physikalische Grundlagen Die Optik befaßt sich mit der Natur des Lichts. Die für das menschliche Auge sichtbaren Lichtstrahlen umfassen den Bereich der Wellenlängen = 380nm bis = 780nm. Sie gehören zu den elektromagnetischen Transversalwellen. Die Wellenlänge ist mit der Frequenz f und der Lichtgeschwindigkeit c verknüpft mit Gl.1: c=f Das Licht breitet sich im Vakuum mit einer Geschwindigkeit von 299 792,458 km/s aus. Lichtstrahlen, die sich in einem homogenen Medium befinden, gehorchen den Gesetzen der geometrischen Optik z.B. dem Reflexionsgesetz, dem Brechungsgesetz etc.. 2.1 Polarisation des Lichts: Natürliches Licht besitzt keine ausgezeichnete Schwingungsebene, es ist nicht polarisiert. Es besteht aus kurzen Wellenzügen, die völlig regellos mit statistisch verteilten Schwingungsrichtungen ausgestrahlt werden. Mit Hilfe eines Polarisators kann man natürliches Licht polarisieren. Der E-Vektor des Lichts schwingt dann in der Ebene des Polarisators. Um die Schwingungsebene bestimmen zu können, benutzt man ebenfalls einen Polarisator, der hier einen Analysator darstellt. Ist die Analysatorrichtung um den Winkel gegenüber der Schwingungsrichtung gedreht, so wird nur die Projektion des E-Vektors E cos vom Analysator durchgelassen (Bild 1). Seite 1 von 10 Versuch 7: Polarisationsmodulation Bild 1: Linear polarisiertes Licht Die Intensität IL bezüglich der Intensität I0 vor dem Analysator beschreibt das Gesetz von Malus: IL = I0 cos2 A Gl.2: 2.2 Der Laser: Das Wort "LASER" ist eine Abkürzung für - Light Amplification by Stimulated Emission of Radiation - und bedeutet (übersetzt) Lichtverstärkung durch stimulierte Emission von Strahlung. Nach Bild 2 kann ein einfallendes Photon der Energie Eph = E2 - E1 (Energieniveau-Abstand) ein Elektron zu einem Übergang vom höheren Niveau E2 zum tieferen E1 veranlassen, das dabei ein Photon der gleichen Energie emittiert. Bild 2: Wechselwirkungen zwischen Photonen und Elektronen in einem Atom Ebenso ist es möglich, daß ein Photon absorbiert wird, und dadurch ein Elektron auf E2, also umgekehrt, angehoben wird. Seite 2 von 10 Versuch 7: Polarisationsmodulation Die beiden Vorgänge - Emission und Absorption - besitzen eine bestimmte Wahrscheinlichkeit. Die Absorptionswahrscheinlichkeit ist proportional zu N1, der Besetzungszahl des unteren Niveaus, und die stimulierte Emissionswahrscheinlichkeit ist proportional zu N2, der Besetzungszahl des oberen Niveaus. Nur bei einer Besetzungsinversion, d.h. N2 > N1 erhält man eine meßbare stimulierte Emission. Die Inversion wird durch sog. Pumpen erzeugt. Dabei werden Elektronen durch Energieabsorption auf höhere Niveaus gehoben. Dies kann durch optisches Pumpen (Festkörperlaser) geschehen, durch thermische Anregung (Gaslaser) oder auch durch Strominjektion (Halbleiterlaser). Alle Photonen koppeln durch diese Stimulation phasengerecht an die vorhandene Welle an, so daß eine kohärente Lichtwelle entsteht. Unser Laser - ein He-Ne-Laser - ist zusätzlich noch linear polarisiert. 2.3 Der Faraday-Rotator: Bringt man eine transparente Substanz, die nicht optisch aktiv ist, zwischen 2 gekreuzte Polarisatoren, so kann durch das System kein Licht hindurchtreten. Legt man nun ein Magnetfeld parallel zur Richtung des Lichtstrahls an, so wird bei einigen Substanzen die Polarisationsrichtung durch den Faraday-Effekt um einen bestimmten Winkel gedreht. Der Winkel ist abhängig von der Magnetfeldstärke H, der Länge l und einer Materialkonstanten Verdet-Konstante - V (V ist eine Funktion von ). Gl.3: =VlH Das magnetische Feld H, das entlang des Lichtstrahls homogen sein soll, wird mit einer Spule mit N Windungen und der Länge l erzeugt. Für das H-Feld gilt, wenn IR der Gesamtstrom durch die Spule bedeutet: Gl.4 H N IR l eingesetzt in Gl.3, ergibt für V: Gl.5: V N IR Nach Gl.2 gilt das Gesetz von Malus: Seite 3 von 10 Versuch 7: Polarisationsmodulation IL = I0 cos2 A , wobei A der Winkel des Analysators gegenüber der Schwingungsrichtung der ankommenden polarisierten Lichtwelle und I0 die Intensität bei A = 0‘ darstellt. Wird nun ein Faradayrotator noch zusätzlich in den Strahlengang eingebracht, so dreht sich die Polarisationsrichtung der Lichtwelle um einen Winkel ; es gilt nach Gl.5: = V N IR Wenn A der Winkel des Analysators zur Lichtwelle ohne Rotatorstrom und E der Winkel nach Einschalten des Rotators bedeutet, so gilt (siehe Skizze): Gl.6: E = A ± , Vorzeichen je nach Stromrichtung im Rotator. Wir benutzen für die weitere Herleitung nur das positive Vorzeichen. Daraus folgt für die Intensität: Gl.7: IL = I0 cos2 ( A + ) = I0 cos2 E = I0 cos2 ( A + V N IR) Da der Kurzschlußstrom der Diode IK proportional der Intensität ist, kann IL = k IK und I0 = k IK0 gesetzt werden; Gl.7 umgestellt und nach E aufgelöst ergibt: Gl.8: E = arccos (IK/IK0)0.5 = A + V N IR Seite 4 von 10 Versuch 7: Polarisationsmodulation 2.4 Wechselstrom-Modulation: Fließt durch die Spule des Faraday-Rotators ein Wechselstrom, so baut sich ein homogenes magnetisches Wechselfeld auf und moduliert über den Faraday-Effekt die Polarisationsrichtung des Laserstrahls. Der Drehwinkel ist proportional zum Wechselstrom. Daraus folgt: = c . sin t Gl.9: mit: c Proportionalitätskonstante Kreisfrequenz des Wechselstroms Ist der Analysator zur Schwingungsebene des Laserstrahls um den Winkel A gedreht, so erhalten wir die Intensität IL = I0 cos2 ( A + ) = I0 cos2 ( A + c . sin t) Gl.10: d.h. die Intensität schwankt im Takt der Modulationsfrequenz ; der Laserstrahl ist amplitudenmoduliert. Mit Hilfe der Additionstheoreme können wir die Formel wie folgt verändern: Gl.11: IL I0 (1 cos( 2 A ) cos( 2c sin( t ) sin( 2 A ) sin( 2c sin t )) 2 Steht die modulierte Größe im Argument einer weiteren sinus- bzw. kosinusförmigen Funktion, so läßt sich die Gesamtfunktion nach Besselfunktionen entwickeln. Die Besselfunktion Jn (1.Art und n-ter Ordnung) ist als unendliche Reihe definiert ( Siehe auch Bild 3): (1) k J n ( ) k 0 k!( n k )! 2 Gl.12: Seite 5 von 10 n2k Versuch 7: Polarisationsmodulation Bild 3: Besselfunktionen 1. Art der Ordnungen 0 bis 3 für Argumente 0 bis 14 Berücksichtigt man die folgenden Entwicklungen für die trigonometrischen Funktionen cos( sin t ) J 0 ( ) 2 J 2 n ( ) cos( 2nt ) : Gl.13: n 1 sin( sin t ) 2 J 2 n 1 ( ) cos(( 2n 1)t ) : Gl.14: n 0 So ergibt sich für die Intensität mit = 2c : Gl.15: IL I0 [1 cos( 2 A ) ( J 0 (2c) 2 J 2 n ( ) cos( 2nt )) 2 n 1 sin( 2 A ) (2 J 2 n 1 (2c) sin[( 2n 1)t ])] n 0 Die obere Zeile der Gleichung 15 enthält Gleichanteile, sowie Komponenten mit geradzahligen Vielfachen der Modulationsfrequenz; die untere Zeile enthält ungeradzahlige Vielfache A stellt den Arbeitspunkt der Modulation dar (Siehe Bild 4) Seite 6 von 10 Versuch 7: Polarisationsmodulation Beträgt A = 0 , so befinden wir uns im Maximum der Funktion IL (siehe Bild 4, Pkt.A). Nach der Gl.15 ergibt sich: Gl.16: I0 I L (1 J 0 (2c) 2 J 2 n ( ) cos( 2nt )) 2 n 1 Da die Besselfunktion mit steigendem n rasch gegen 0 geht (siehe Bild 3), können wir aus der Gl.16 ableiten, daß der Hauptanteil der Modulation im wesentlichen die doppelte Frequenz 2 besitzt: IL(t) ~ I0 cos (2t) Dies läßt sich am Oszilloskop experimentell feststellen. (Siehe Bild 4, I1) Liegt A zwischen 0 und 45, so nimmt der Anteil der ungeraden Frequenzen zu. Da die Funktion IL = I0 cos2( E) in einem breiten Bereich um 45 nahezu linear verläuft, erhalten wir im wesentlichen eine Komponente bei der Frequenz . Nur in den Bereichen um die Extrema wird die Abbildung erheblich verzerrt. Der optimale Arbeitspunkt für näherungsweise lineare Übertragung liegt bei 45 bzw. bei 135. Mit Gl.15 erhalten wir eine Funktion IL der Form: Gl.17: IL I0 I 0 J 2 n 1 (2c) sin(( 2n 1)t ) : 2 n 0 Das übertragene Signal ist also bei 45° gegenphasig zu , bei 135° in Phase zu (Siehe Seite 7 von 10 Versuch 7: Polarisationsmodulation Experiment). Unter Vernachlässigung der höheren Frequenzkomponenten folgt: I L (t ) ~ I 0 sin(t ) 2.5 Demodulation mit einer PIN-Photodiode: Mit Hilfe einer Photodiode wird die schwankende Intensität des Laserstrahls in einen Wechselstrom umgewandelt. Da die Wechselströme in unserem Fall (Si-PIN-Diode) zwischen 0.1 und 0.8 mA liegen, benötigen wir noch einen Wechselstrom-Vorverstärker mit einer Versorgungsspannung von 10V. Danach wird das Signal mit einem NF-Verstärker nochmals mehrfach verstärkt, um einen Lautsprecher ansteuern zu können. Photodioden werden in der Meß- und Regelungstechnik sowie bei der optischen Nachrichtenübertragung eingesetzt. Überwiegend benutzt man Festkörperdetektoren zur Demodulation optischer Signale. Bei Glasfasersystemen hat man sich wegen der geringen Dämpfung der Fasern auf 3 Spektralbereiche spezialisiert: a) 0.85 μm (2 dB/km) b) 1.3 μm (0.35 dB/km) c) 1.5 μm (0.2 dB/km) Untersucht man die relative, spektrale Empfindlichkeit der Si-PIN-Diode, die wir verwenden, so läßt sich ein Maximum bei 850 nm feststellen (Siehe Bild 5). Bild 5: Relative spektrale Bild 6: Aufbau einer PIN-Diode Empfindichkeit Seite 8 von 10 Versuch 7: Polarisationsmodulation Wir arbeiten mit einem HeNe-Laser mit der Wellenlänge = 632.8 nm . Bei dieser Wellenlänge erhält man eine relative Empfindlichkeit der Photodiode von 65%. In Bild 6 ist der Aufbau einer PIN-Photodiode schematisch skizziert. Es handelt sich dabei um einen pn-Übergang, der durch eine verhältnismäßig dicke Schicht (i,intrinsic), einer undotierten, eigenleitenden Zone, erweitert wurde. In dieser raumladungsfreien Zone fällt die angelegte Sperrspannung ab und bewirkt ein konstantes Feld, das die optisch erzeugten Elektron-Loch-Paare trennt. Diese Ladungsträger-Sammelzone besitzt einen hohen Sammelwirkungsgrad und kurze Sammelzeiten. Es können bei guter Optimierung und Abstimmung auf die verwendtete LaserfrequenzModulationsfrequenzen bis zu 20 GHz und mehr verarbeitet werden. In Bild 7 ist die Beziehung zwischen Leerlaufspannung UL bzw. Kurzschlußstrom der Photodiode IK und der Beleuchtungsstärke EV (EV proportional zur Intensität) dargestellt. Deutlich ist die Proportionalität des Kurzschlußstroms zu der Beleuchtungsstärke zu erkennen. Bild 7: 3 Arbeitsprogramm 3.1 Aufgaben 1. Bestimmen Sie die Intensität des Laserstrahls in Abhängigkeit vom Winkel A des Analysators mit der Photodiode D1 (Typ BPW34 ohne Verstärker) im Bereich 0 10- Schritten. Tragen Sie den Diodenstrom IK der proportional zur Intensität bzw. Bestrahlungsstärke ist, über den Winkel A in einem Diagramm auf! 2. Bestimmen Sie die Verdet-Konstante V des Faraday-Rotators nach der unten beschriebenen Methode (siehe auch Erläuterungen auf Seite 3). Einheit für Magnetfeldstärke H: A/m Seite 9 von 10 360 in Versuch 7: Polarisationsmodulation Hinweis: Verwenden Sie für diesen Versuch die Buchsen am Verstärker für Gleichspannung 0-18V. Bitte maximal 4A einstellen!! Messung: a) Es wird zunächst der Diodenstrom IK bei der Analysatorstellung 45 und bei einem Rotatorstrom IR von 0 - 3A in 0,3A-Schritten erfaßt. b) Aus den Diodenströmen IK errechnen Sie den Winkel E mit Gl.8, wobei IK0, der Diodenstrom bei A = 0, aus der 1. Aufgabe entnommen wird. c) Nun tragen Sie E über IR in einem Diagramm auf und bilden eine Ausgleichsgerade. d) Die Steigung der Ausgleichsgerade m errechnet sich nach Gl.8 : m = N V; mit N = 955 ergibt sich für die Verdet-Konstante: V m Winke lg rad 955 A 3. Modulieren Sie den Laserstrahl mit einer Wechselspannung von 2V (50Hz) und untersuchen Sie das Frequenz- und Phasenverhalten des demodulierten Signals am Vorverstärker-Ausgang des Detektors KD1 in Abhängigkeit des Analysatorwinkels A mit Hilfe eines Oszilloskopes. Diskutieren Sie die Spezialfälle! 4. Bauen Sie die Apparatur so um, daß Sie den Laserstrahl mit der Tonfrequenz eines Radio-Lautsprecherausgangs modulieren können. 3.2 Fragen (Bitte schriftlich beantworten !) 1) Erklären Sie den Begriff „Polarisation“ 2) Was versteht man unter dem Faraday-Effekt 3) Skizzieren Sie den Aufbau der Signalübertragungsstrecke von Aufgabe 4 und erklären Sie die Arbeitsweise der einzelnen Elemente ! Seite 10 von 10