svcrproc11
Werbung

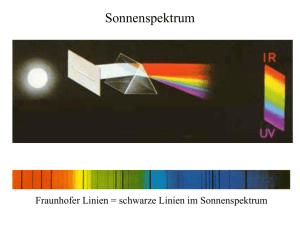
Labor Technische Optik – Versuch 3 Versuch 3: Photospektrometer © Prof. Dr. Alexander Hornberg, Dipl.-Phys. Hermann Bletzer Abb. 1. Photospektrometer von Fa. Shimadzu Versuch 3 – Photospektrometer ................................................................1 1. Grundlagen ..........................................................................................2 1.1 Absorption.....................................................................................2 1.2 Photospektrometer ........................................................................3 1.2 Bestimmung der Dicke von optisch transparenten Schichten .......3 Literatur...................................................................................................6 Was Sie schon immer wissen wollten Optisches Medium, Transmissionsgrad, Reintransmissionsgrad, Absorptionsgrad, Strahlungsleistung, Reflexionsgrad, Monochromator, Interferenz, Phasensprung Stand: 14.05.2016 2 © Prof. Dr. Alexander Hornberg, Dipl.-Phys. Hermann Bletzer 1. Grundlagen 1.1 Absorption und Reintransmissionsgrad Ein optisches Medium - z.B. Glas, Kunststoffe, eine mit Flüssigkeit gefüllte Küvette - hat im allgemeinen einen von der Wellenlänge abhängigen Transmissionsgrad (= Druchlässigkeitsvermögen) t (l ) . Abb. 2. Reflexion, Brechung und Absorption an einer Platte Der spektrale Transmissionsgrad ist definiert: t (l ) = (F l ) t (F l )i (0.1) Hierbei bedeuten (F l )i die einfallende und (F l )t die durch das Medium durchgelassene spektrale Strahlungsleistung. Da der spektrale Transmissionsgrad oft über mehrere Zehnerpotenzen variiert, wird oft die spektrale optische Dichte é 1 D (l ) = lg ê êët (l ù ú )ú û (0.2) dargestellt. Betrachten wir nur absorbierende Stoffe, dann muss zwischen dem gemessenen Transmissionsgrad t (l ) und dem Reintransmissionsgrad t i (l ) unterschieden werden. Beim Übergang der Strahlung zwischen optischen Medien mit verschiedenem Brechungsindex treten nämlich Reflexionsverluste auf. Der spektrale Reflexionsgrad ist definiert: r (l ) = (F l )r , (F l )i 2 æn - n 2 ö ÷ wobei für senkrecht en Einfall r (l ) = çç 1 ÷ èn1 + n 2 ø (0.3) ist mit den Brechungsindizes n 1 und n 2 der aneinandergrenzenden Medien. Die Schwächung infolge Absorption beim Durchgang durch das optische Medium der Dicke wird durch das Lambert-Beer-Gesetz beschrieben: t i (l ) = * (F l )ex = e - k (l )d = 10- k (l )d = 1 - a (l ) (F l )i (0.4) Dabei ist der spektrale dekadische Absorptionskoeffizient k * (l ) = lg(e ) ×k (l ) = 0.4343 ×k (l ) . Die spektrale (dekadische) Extinktion E (l ) ist dann Versuch 3: Photospektrometer é 1 E (l ) = lg ê êët i (l ù ú = k * (l )d )ú û 3 (0.5) Da die Kurvenform der spektralen Extinktion von der Dicke d abhängt, wählt man die spektrale (dekadische) Diabatie q(l ) = 1 - lg E (l ) = 1 - lg [k *(l )d ] = 1 - lg k *(l ) - lg d (0.6) als Darstellung des Absorptionsverhaltens. Die Kurvenform der spektralen Diabatie ist unabhängig von der Dicke. Da die Dicke d nur einen Offset - lgd liefert, ist die Kurvenform der spektralen Diabatie unabhängig von der Dicke. Wird die Absorption einer Lösung gemessen, dann ist - für nicht zu hohe Konzentration c des gelösten Stoffes - E von c linear abhängig: E (l ) = e * (l ) ×c ×d (0.7) Man nennt e * (l ) den konzentrationsbezogenen Absorptionskoeffizienten. Der spektrale Transmissionsgrad einer Platte berücksichtigt die Reflexionsverluste an der Oberfläche als auch die Absorptionsverluste im Innern der Platte. Unter Berücksichtigung von Mehrfachreflexionen gilt in guter Näherung t i (l ) = t (l ) P (l ) mit dem Reflexionsfaktor P (l ) = 1 - r (l ) 2n n = 2 1 22 1 + r (l ) n1 + n 2 (0.8) 1.2 Spektralphotometer Ein Spektralphotometer gestattet die direkte Messung des spektralen Transmissionsgrades t (l ) . Aus dem Spektrum einer Lichtquelle (Wolfram- oder Deuteriumlampe) wird mit Hilfe eines Monochromators monochromatisches Licht erzeugt. Die Wellenlänge ist - je nach Gerätekonstruktion - durchstimmbar. Das für den Versuch verwendete Photometer überdeckt den Spektralbereich von 200 bis 900 nm. Die Eigenschaften der Lichtquelle, der optisch dispersiven Bauelemente (Gitter) und der Strahlungsempfänger sind von der Wellenlänge abhängig. Außerdem tritt durch Alterung von Lichtquellen und Strahlungsempfängern eine zeitabhängige Veränderung der Empfindlichkeit der Messanordnung ein. Um diese Effekte bei der Messung zu eliminieren, verwendet man ein Zweistahlphotometer. Bei diesem wird die spektrale Strahlungsleistung des Probenkanals (F l )t mit der des Referenzkanals (Vergleichskanal) (F l )0 verglichen. 1.2 Bestimmung der Dicke von optisch transparenten Schichten Eine weitere Anwendung des Spekralphotometers ist die heute weit verbreitete Methode der Schichtdickenmessung durch Interferenzmessung. In der Halbleitertechnik ist die Schichtdicke von SiO2 auf Wafern ein häufig verwendetes Kriterium für die Qualitäts- und Produktionskontrolle. Solche SiO2 -Schichten beeinflussen wesentlich die Eigenschaften von Epitaxialschichten. 4 © Prof. Dr. Alexander Hornberg, Dipl.-Phys. Hermann Bletzer Abb. 3. Die Messung der Schichtdicke d durch Interferenzmessung mit einem Spektralphotometer und einem Reflexionszusatz mit a = 5o ist eine beliebte Methode, da sie ausreichend genau, zerstörungsfrei und nur mit geringem Arbeitsaufwand verbunden ist. Man kann in Transmission (Probenkanal und Referenzkanal) oder in Absorption (nur Probenkanal) messen. An der Skizze liest man 2a 1 + 90o - a = 180o und d + a 1 = 90o ab, daraus ergibt sich d = 45o - a / 2 . Die beiden an der Grenzschicht Luft/SiO2 bzw. SiO2/Si reflektierten Strahlen überlagern sich. Optischer Wegunterschied: (0.9) D lopt = 2n A B - A D Der Phasensprung von bei Reflexion am optisch dichteren Medium tritt bei beiden Reflexionen auf, damit hat er keinen Einfluss auf die Interferenz. Bedingung für Minimum: ( D lopt = 2n A B - A D = m + 1 l 2 ) , m = 0, 1, 2, K Aus sin a = n sin b folgt und AB = d cos b , A D = A C sin a (0.10) Versuch 3: Photospektrometer D lopt = 2n d d - 2 sin b sin a cos b sin b nd = 2n n 2 - sin 2 a - 2 sin 2 a n 2 - sin 2 a n nd = 2d n 2 - sin 2 a und schließlich ( 2d n 2 - sin 2 a = m + 1 l 2 ) Wir haben zwei Unbekannte: die Dicke d und die Ordnungszahl m. Daher vergleicht man zwei Wellenlängen 1 und 2, die beide zu einem Minimum führen. ( 2d n 12 - sin 2 a = m 1 + 1 l 2 ) , ( 2d n 22 - sin 2 a = m 2 + 1 l 2 ) Die Differenz liefert æ n 2 - sin 2 a 2d ççç 1 l1 çè n 22 - sin 2 a l2 ö ÷ ÷ = m1 - m 2 = N ÷ ÷ ø oder d = N l 1l 2 × 2 2 2 l 2 n 1 - sin a - l 1 n 22 - sin 2 a Wir nehmen an, wir haben in der Messkurve bei 1 ein Minimum der Ordnung m1. Das Minimum bei der zunächst größeren Wellenlänge muss die Ordnung m 1 - 1 = m 2 haben, da die Dicke konstant ist. Damit gibt die Anzahl der Maxima, die zwischen 2 Minima liegen, die Änderung N = m 1 - m 2 der Ordnungszahl an. Unter Vernachlässigung der Dispersion, d. h. n 1 = n 2 , erhält man als Dicke d = - 1 1ö æ1 ÷ ç ÷ ÷ 2 n 2 - sin 2 a çè l 1 l 2 ø N 2. Arbeitsprogramm 1. Messen Sie die Dicke einer SiO2 -Schicht ( n = 1.55 ) bei zwei verschiedenen Wafern. 5 6 © Prof. Dr. Alexander Hornberg, Dipl.-Phys. Hermann Bletzer 2. Bei welcher Interferenzordnung haben Sie die Schichtdicken der Wafer gemessen? 3. Messen Sie den spektralen Transmissionsgrad t (l ) von je zwei Kanten- und Bandfiltern 4. Bestimmen Sie den Reintransmissionsgrad t i bei der Kantenwellenlänge l c bzw. Mittenwellenlänge l m . 5. Messen Sie t (l ) eines Interferenzfilters und bestimmen sie dessen Halbwertsbreite. 6. Vergleichen Sie den Transmissionsgrad von 2 Polarisationsfiltern, die hintereinander angeordnet sind bei 0 (hell-Abgleich), 45 und 90 (gekreuzt). 7. Bei welchen Wellenlängen 0 liefern die Filter optimal polarisiertes Licht und berechnen Sie die Änderung der Polarisationsgrads. p(l 0 ) = t p (l 0 ) - t s (l 0 ) t p (l 0 ) + t s (l 0 ) 8. Ermitteln Sie die Zeitkonstante eines phototropen Brillenglasses. Phototrope Gläser gehören zu den optischen Spezialgläsern. Sie verringern bei Einwirkung kurzweiliger Strahlung ihren Transmissionsgrad, kehren aber nach Abschluß der Bestrahlung wieder reversibel in den Ausgangszustand zurück. Diese Gläser enthalten geringe Mengen von Silberhalogeniden ähnlich den fotografischen Schichten, nur sehr viel feiner -. Durch Belichtung mit kurzwelligem Licht, bevorzugt im Bereich 300 - 400 nm (Sonne, Blitzlicht, Xenonlampe) sinkt der Transmissionsgrad von z.B. 0.8 auf 0.5 (dickenabhängig), indem aus dem Silberhalogenid metallisches Silber freigesetzt wird. Bei starker Bestrahlung nimmt der Transmissionsgrad solange ab, bis ein Gleichgewicht mit der Rückreaktion (Regeneration) erreicht ist. Die Regenerierung kann durch Wärme und Einstrahlung von langwelligem Licht beschleunigt werden. 9. Wodurch ist die langwellige Empfindlichkeitsgrenze des Strahlungsempfängers im Spektralphotometer festgelegt? Erläutern sie die prinzipiellen Vorgänge, die zum elektrischen Signal des Strahlungsempfängers führen. Literatur 1. F. Pedrotti, et. al., Optik für Ingenieure, Springer 2002, ISBN 3-540-67279-2, Kapitel 16 und 17.