Einführung in die Integralrechnung

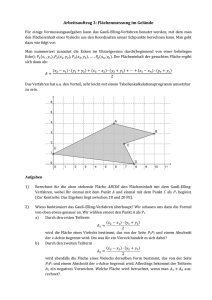
Einführung in die Integralrechnung
Von Florian Modler
In diesem Artikel will ich euch einen ersten
Einblick in die Integralrechnung geben.
Dieser Artikel ist speziell für Schüler
geschrieben.
Ich habe mich bemüht diesen Artikel vor
allem verständlich und anschaulich zu
gestalten.
Ich hoffe mir ist dieses gelungen.
Dieser Artikel umfasst nur einen ersten
Einblick in die Integralrechnung, die man so
in der Oberstufe eines Gymnasiums
(12. Klasse) kennen lernt.
Es gibt noch viele Gebiete, in denen man die
Integralrechnung anwenden kann. Deswegen
wird es auf jeden Fall noch einen zweiten
Teil geben.
Vielleicht kommt auch noch ein dritter und vierter Teil. Das kann man nie ausschließen.
Aber jetzt erstmal viel Spaß mit meiner kleinen Einführung in die Integralrechnung.
Inhalt
1 Erste Berechnungen einer Fläche im Graphen
2 Der Begriff des Integrals
2.1 Geometrische Definition des Integrals
2.2 Analytische Definition des Integrals
3 Rechenregel für Integrale
3.1 Faktorregel
3.2 Summenregel
3.3 Intervalladditivität
4 Verwenden der Integrale zur Flächenberechnung
5 Flächenberechnung zwischen 2 Graphen
6 Zusammenfassung Teil I
7 Abschluss
8 Quellenangabe
1 Erste Berechnungen einer Fläche im Graphen
Um den Begriff des Integrals einführen zu können, muss ich etwas weiter ausholen. Und zwar
soll zuerst die schwarz markierte Fläche unter dem Graphen berechnet werden.
Die Funktion des Graphen ist y=x.
(1 Einheit=1 cm)
Man sieht die Antwort sofort: A=0,5 cm².
Es gibt mehrere Möglichkeiten, um zu dieser Antwort zu gelangen. Zwei möchte ich hier
ganz kurz anführen:
1. Möglichkeit: Wir berechnen den Flächeninhalt des Quadrats (1 cm x 1 cm) und halbieren
diesen Flächeninhalt, da das Quadrat durch die Funktion y=x halbiert wird.
2. Möglichkeit: Wir berechnen den Flächeninhalt des Dreiecks mit folgender Formel:
gh
A
, g ist dabei 1 cm und h ebenfalls 1 cm, so kommen wir auf A=0,5 cm²
2
Nun berechnet bitte folgenden Flächeninhalt der schwarz markierten Fläche:
Die Funktion des Graphen ist y=x².
Mit unseren Quadraten und Dreiecken kommen wir hier nicht weit.
Vielleicht kennt ihr die Methode, die ich jetzt anführen werde, schon aus dem Bereich
Geometrie, wo ihr den Flächeninhalt des Kreises abschätzen solltet, um zu Pi zu gelangen.
Vorgehensweise:
1. Zuerst teilen wir die Fläche in 4 Säulen ein, die unter dem Graphen liegen. (Untersumme)
2. Nach diesem Schritt teilen wir den Graphen noch einmal in 4 Säulen ein, die auch über dem
Graphen verlaufen und bilden daraus einen Mittelwert. (Obersumme)
Die Funktion ist ebenfalls y=x².
Nun berechnen wir die Obersumme und die Untersumme. Da wir die Breite (0,25) kennen,
wissen wir durch den entsprechenden Funktionswert auch die Höhe einer Säule:
Die Summe der Säulen unterhalb des Graphen wird als Untersumme bezeichnet.
Es gilt: S4  A
S4 
1 9 1 1 1 1
9
1
1 9  4  1 14 7
     
 



 0, 21875
4 16 4 4 4 16 64 16 64
64
64 32
Die Summe der Säulen oberhalb des Graphen wird als Obersumme bezeichnet.
Es gilt: A  S4
S4 
1 9 1 1 1 1 1
7 1 7
8 15
      1 
 


 0,343375
4 16 4 4 4 16 4
32 4 32 32 32
Der gesuchte Flächeninhalt A wird von S 4 und S4 eingeschachtelt.
7
15
 A .
Als Abschätzung ergibt sich:
32
32
Die Abschätzung kann durch Mittelwertbildung verbessert werden:
7 15

32
32  11  0,34375
A
2
32
Nun haben wir den Flächeninhalt ungefähr berechnet, indem wir nämlich 4 Säulen gewählt
haben. Um den Flächeninhalt noch genauer auszurechnen nehmen wir nicht 4 Säulen, sondern
n Säulen.
Und verfahren genauso wie bei der Berechnung mit 4 Säulen:
1 1 1 2
1 3
1 n 1
   ( )²   ( )²  ...   (
)²
n n² n n
n n
n
n
1 1
1
1
   4   9  ...  (n  1)² 
n³ n³
n³
n³
1
 (1  4  9  ...  ( n  1)²)
n³
Sn 
An dieser Stelle müssen wir eine Formel verwenden, die ihr der Formelsammlung entnehmen
könnt oder die ihr eventuell schon einmal bei dem Thema „Vollständige Induktion“ gesehen
habt.
(1  4  9  ...  (n  1)²) 
(n  1)n(2n  1)
6
Also rechnen wir mit dieser Formel weiter:
Sn 
1 (n  1)n(2n  1) (n  1)(2n  1) 2n²  3n  1 1 1
1



 

n³
6
6n ²
6n²
3 2n 6n²
Für die Obersumme dementsprechend verwenden wir diese Formel:
(1  4  9  ...  n²) 
1 (n  1)n(2n  1)

n³
6
Also:
1 1 1 2
1 3
1
   ( )²   ( )²  ...   n²
n n² n n
n n
n
1 1
1
1
   4   9  ...  n² 
n³ n³
n³
n³
1
1 (n  1)n(2n  1)
 (1  4  9  ...  n²)  
n³
n³
6
(n  1)(2n  1) 2n²  3n  1 1 1
1


 

6n ²
6n ²
3 2n 6n ²
Nun lassen wir n gehen Unendlich streben, da wir unendlich viele Säulen verwenden wollen.
Dafür gilt:
Sn 
Für n   geht
1
1
1 1
1
1 1
1



 und 
 .
3 2n 6n ²
3 2n 6n ²
3
3
Dies bedeutet für die Abschätzung von A:
1
1
1
 A  , alsoA  .
3
3
3
Als Übung folgende Aufgabe an euch:
Berechne den Flächeninhalt A der vom Graphen f(x)=x³, der x-Achse und der Geraden x=1
begrenzt wird.
Hilfe: (1  8  27  ...  ( n  1)³) 
1 (n  1)²  n²
1
1 (n  1)²  n²

und 4 (1  8  ...  n³)  4 
4
n
4
n
n
4
Lösung:
1 n 1
1 3
1 1 1 2
)³
   ( )³   ( )³  ...   (
n
n
n n
n n³ n n
1
1
1 1
 4  4  8  4  27  ...  ( n  1)³ 
n³
n
n n
1
 4 (1  8  27  ...  ( n  1)³)
n
1
1 (n  1)²  n ² (n  1)² n ²  2n  1 1 1

 


 4
4 2n 4n²
4n ²
4n ²
4
n
1
1 3
1 1 1 2
S n     ( )³   ( )³  ...   n³
n
n n
n n³ n n
1
1
1 1
 4  4  8  4  27  ...  n ³ 
n
n
n n
1 (n  1)²  n ²
1
 4 (1  8  ...  n³)  4 
4
n
n
1
(n  1)² n ²  2n  1 1 1

 


4 2n 4n ²
4n ²
4n ²
1 1
1
1
1 1
1
1

 und 

 .
Für n   geht 
4 2n 4n ²
4
4 2n 4n ²
4
Sn 
Dies bedeutet für die Abschätzung von A:
1
1
1
 A  , alsoA  .
4
4
4
Nun haben wir aber den Flächeninhalt nur im Intervall [0;1] berechnet. Wie sieht der
Flächeninhalt aber im Intervall [0;2] oder [0;b] aus?
Um diese Frage zu klären, nehmen wir wieder die Funktion f(x)=x³ und erhalten wir die
Obersumme und Untersumme im Intervall [0;2]:
2 2
2
2
2 2(n  1)
S n   ( )³   (2  )³  ...   (
)³
n n
n
n
n
n
16
16
16
 4   4  8  ...  4  (n  1)³
n
n
n
16
16 (n  1)²  n² 4(n²  2n  1)
 4  (1  8  ...  (n  1)³)  4 

n
n
4
n²
8 4
 4 
n n²
2 2
2
2
2 2n
S n   ( )³   (2  )³  ...   ( )³
n n
n
n
n
n
16
16 (n  1)²  n² 4(n ²  2n  1)
 4  (1  8  ...  n ³)  4 

n
n
4
n²
8 4
 4 
n n²
Für
8 4
8 4
n   : 4    4und 4    4
n n²
n n²
A4
2
, weil wir die Länge 2 in n
n
Säulen unterteilt haben und dafür ändert sich der jeweilige Funktionswert, also auch die Höhe
der Säule.
Klingt ja auch logisch, denn die Breite einer Säule ist ja nun
Allgemein im Intervall [0;b] heißt das:
b b
b
b
b b(n  1)
Sn   ( )³   (2  )³  ...   (
)³
n n
n
n
n
n
b4
b4
b4
 4   4  8  ...  4  (n  1)³
n
n
n
4
b
b 4 (n  1)²  n² b 4  (n  1)² b 4  (n²  2n  1)
 4  (1  8  ...  ( n  1)³)  4 


n
n
4
4  n²
4  n²
4
4
4
b b
b
 

4 2n 4n ²
b b
b
b
b bn
Sn   ( )³   (2  )³  ...   (
)³
n n
n
n
n
n
b4
b4
b4
 4   4  8  ...  4  (n³
n
n
n
4
b
b 4 (n  1)²  n² b 4  (n  1)² b 4  (n²  2n  1)
 4  (1  8  ...  n³)  4 


n
n
4
4  n²
4  n²
4
4
4
b
b
b
 

4 2n 4n ²
Für
n :
A
b4 b4 b4
b4
b4 b4 b4
b4


 und 


4 2n 4n ²
4
4 2n 4n ²
4
b4
4
Berechne den Flächeninhalt A der Fläche, die von der Funktion f(x)=x³, der x-Achse, der
Geraden x=2 und der Geraden x=3 begrenzt wird.
Lösungen:
A
34 24 65
 
 16, 25
4 4
4
Berechne den Flächeninhalt A der Fläche, die von der Funktion f(x)=x, der x-Achse und der
Geraden x=b begrenzt wird.
Lösungen:
A
b²
2
2 Der Begriff des Integrals
2.1 Geometrische Definition des Integrals
Orientierter Flächeninhalt – Definition des Integrals:
- Flächeninhalte oberhalb der x-Achse haben ein positives Vorzeichen.
- Flächeninhalte unterhalb der x-Achse haben ein negatives Vorzeichen.
BILD!
Definition:
Gegeben sei eine Funktion f, die über einem Intervall [a; b] definiert ist, dann versteht man
unter dem Integral der Funktion von a bis b die Summe der orientierten Flächeninhalte
zwischen dem Graphen von f, der x-Achse und der Geraden x=a und x=b.
Schreibweise:
b
b
a
a
 f   f ( x)dx   A1  ( A2)  A3  ( A4)
a : untereGrenze
b : obereGrenze
Wie liest man das? So: „Integral von a bis b der Funktion f“
Grundintegrale:
b
b
b
b² a ²
 ; 1dx  b  a
2 2 a
b4 a 4
b³ a ³
x
³
dx

 ;  x ² dx  
a
4 4 a
3 3
 xdx 
a
b
2.2 Analytische Definition des Integrals
Analytische Definition des Integrals:
Die Funktion f sei über dem Intervall [a; b] definiert und dort beschränkt. Dann versteht man
unter dem Integral von a bis b der Funktion f eine Zahl, die man folgendermaßen erhält:
(1) Man bildet die Zerlegung Zn des Intervalls [a; b] in n gleich lange Teilintervalle.
(2) Man bildet die zu Zn gehörende Obersumme Sn und die Untersumme Sn. Insgesamt erhält
man eine Folge von Obersumme Sn und Untersumme Sn ,
(3) Wir bilden lim Sn und lim S n .
n 
n 
Stimmen beide Grenzwerte überein, das heißt ist: lim Sn  lim Sn , so heißt dieser gemeinsame
n 
n 
Grenzwert das Integral von a bis b der Funktion f.
b
Man schreibt:

a
b
foder  f ( x )dx .
a
3 Rechenregeln für Integrale
3.1 Faktorregel
4
Nun berechnet doch einmal folgendes Integral
 2 x³dx .
1
Das neue besteht jetzt darin, dass die Funktion nicht mehr heißt f(x)=x³, sondern f(x)=2x³.
Durch geometrische Überlegungen kommt man jedoch zu dem Schluss, dass der
Flächeninhalt verdoppelt werden müsste.
4
4
44 14
1
3
2
x
³
dx

2

x
³
dx

2(
 )  2(16  )  2 15  31,5
1
1
4 4
4
4
Prüfen wir dies doch mit unserer Berechnung von Obersumme und Untersumme:
Sn 
b
b
b
2b
b
b(n  1)
 2  ( )³   2  ( )³  ...   2  (
)³
n
n
n
n
n
n
b4
(1  8  ...  (n  1)³)
n4
b 4 (n  1)² n ²
b4 b4 b4
2 4 
2  
n
4
4 n 2n ²
b
b
b
2b
b
bn
Sn    2  ( )³   2  ( )³  ...   2  (
)³
n
n
n
n
n
n
b4
 2 4 (1  8  ...  n³)
n
b 4 (n  1)² n²
b4 b4 b4
2 4 
2  
n
4
4 n 2n ²
4
4
b b
b4
b4
b4 b4 b4
b4
Fürn   : 2  
 2 und 2  
2
4 n 2n ²
4
4 n 2n ²
4
2
b4
verdoppelt wird. Also stimmt unsere Überlegung.
4
Zwei weitere Beispiele:
Wir sehen, dass
4
4
 3x²dx  3   x²dx
1
1
4
4
1
1
 cxdx  c   xdx
So kommen wir zur so genannten Faktorregel.
Faktorregel
b
b
 cf ( x)dx  c   f ( x)dx
a
a
b
b
a
a
kurz :  cf  c   f
3.2 Summenregel
Es gibt noch weitere Rechenregeln für Integrale, zum Beispiel die Summenregel.
Summenregel für Integrale:
b
b
b
 ( f ( x)  g ( x))dx   f ( x)dx   g ( x)dx
a
a
a
b
b
b
a
a
a
kurz :  ( f  g )   f   g
Eine Summe wird gliedweise integriert.
3.3 Intervalladditivität
Schaut euch bitte folgende Integrale und ihre Lösungen an:
3
1
3³ 1³
1
2
1³ 3³ 1
2
x
²
dx



9


8
und
   9  8
1

3 3
3
3
3 3 3
3
3
b
b
b³ a ³
b³ a ³
a ³ b³
b³ a ³
a x²dx  3  3  [ 3  3 ]und a 3  3   3  3
a
a³
a³
 x²dx  3  3
0
a
Aus diesen Beispielen folgt folgende Definition:
Definition 1:
a

(1) Ist a<b, so sei
b
b
f ( x)dx    f ( x)dx
a
1
3
3
1
Bsp.:  x ² dx    x ² dx  (
3³ 1³
26
2
 )
 8
3 3
3
3
a
 x²dx 0
(2)
a
3
Bsp.:  x ³dx 0
3
Außerdem gilt.
Allgemeine Regel der Intervalladditivität:
b
c
c
 f ( x)dx   f ( x)dx   f ( x)dx
a
b
a
9
3
4
9
Bsp.:  x ² dx   x ² dx 
3
 x ²dx
4
(a, b, c können beliebig sein.)
Das a, b und c beliebig sein können, führe ich folgenden Beweis an:
c

b
a
a
a
a
c
b
f ( x)dx   f ( x)dx   f ( x)dx |   f ( x)dx |   f ( x)dx
c
a
b
c
a
  f ( x)dx   f ( x)dx    f ( x)dx | nachDef 1
b
b
c
b
c
c
a
b
a
 f ( x)dx   f ( x)dx   f ( x)dx
Damit ihr diese Rechenregeln für Integrale beherrscht, müsst ihr Üben! Dazu eine kleine
Aufgabe. Vereinfacht folgendes Integral:
1
4
2
1
 (3x²  5x  4)dx   (3x²  5x  4)dx
Lösung:
1
4
4
4
4
4
2
1
2
2
2
2
 (3x²  5x  4)dx   (3x²  5 x  4)dx   (3x²  5 x  4)dx  3  x²dx  5  xdx  4  1dx
 (Grund int egrale)  78
Nun kommt es noch viele „Spielereien“, die man mit den Rechenregeln berechnet könnt:
So löst folgende Aufgaben:
1) Welches k erfüllt die Gleichung?
k
a)  ( x  1)dx  2
1
Lösung:
k
a )  ( x  1)dx  2
1
k ² (1)²

 k 1  2
2
2
k²
1
 k   2 | 2
2
2
k ²  2k  1  0
p, q  Formel :
k1,2  1
4 Verwenden von Integralen zur
Flächenberechnung
Der Graph f(x)=x²-3 schließt mit der x-Achse eine Fläche ein.
Berechne den Flächeninhalt der gesamten Fläche zwischen dem Graphen und der x-Achse
Vorgehensweise:
1. Zuerst sollten wir uns eine Zeichnung machen, um den Sachverhalt zu verdeutlichen.
2. Um die Integralgrenzen zu bekommen, müssen wir die Nullstellen berechnen.
0  x²  3
x  3
3. Nun stellen wir das entsprechende Integral auf, um den Flächeninhalt berechnen zu können.
Aufgrund der Achsensymmetrie berechnen wir erstmal das Integral von 0 bis 3 und
multiplizieren das Ergebnis mit 2.
3
|
3
3
 ( x²  3)dx ||  x²dx  3  1dx | | 2 
0
0
0
A  2 3  2 3  4 3
3 | 2  3
5 Flächenberechnung zwischen 2 Graphen
1. Berechne den Inhalt der von dem Graphen von f und g eingeschlossenen Fläche.
f(x)=x²; g(x)=-x+2
Vorgehensweise:
1. Auch hier zeichnen wir uns wieder eine Skizze, um uns den Sachverhalt zu verdeutlichen.
2. Um die Integralgrenzen zu erhalten, bestimmen wir die Schnittpunkte der Graphen.
x²   x  2
x²  x  2  0
p, q  Formel
1
9
1
3
x1, 2    
 
2
4
2
2
x1  1
x 2  2
3. Man sieht leicht:
x2
x2
x1
x1
 g ( x)dx   f ( x)dx
Also gilt:
2
2
1
1
A |  ( x  2)dx   x ² dx || 1  (
| 1,5  6  3 || 4,5 | 4,5
2² 1
(2)³ 1
 )6(
 )|
2 2
3
3
Satz 1
Ist f(x)>g(x) für alle x mit a<x<b, das heißt verläuft der Graph von f zwischen a und b
oberhalb von g, so gilt für den Flächeninhalt A der von beiden Graphen über dem Intervall
[a; b] eingeschlossenen Fläche
b
A   ( f ( x)  g ( x))dx
a
6 Zusammenfassung Teil I
Fassen wir noch einmal zusammen, was wir bis jetzt wissen:
1. Grundintegrale:
b
 x³dx 
a
b
b4 a 4
b³ a ³
 ;  x ² dx  
4 4 a
3 3
b
b
b² a ²
a xdx  2  2 ; a 1dx  b  a
2.Rechenregel:
2.1 Faktorregel:
b
b
a
a
 c  f ( x)dx  c  f ( x)dx
2.2 Summenregel
b
b
b
a
a
a
 ( f ( x)  g ( x))dx  f ( x)dx   g ( x)dx
3.Vereinfachungen:
b
f
a
a
  f
b
a
f
0
a
4. Intervalladditivität:
b
c
c
a
b
a
 f  f  f
a, b, c können beliebig sein.
5. Verwenden von Integralen zur Flächenberechnung:
f(x)=x²-3 [0; 3]
Vorgehensweise:
1. Zuerst berechnet man die Nullstellen.
2. Danach stellt man die entsprechenden Integrale mit den Integralgrenzen auf.
3. Zum Schluss stellt man die Grundintegrale auf und addiert die einzelnen Flächeninhalte.
6. Flächeninhalt der Fläche zwischen zwei Funktionsgraphen:
Satz 1
Ist f(x)>g(x) für alle x mit a<x<b, das heißt verläuft der Graph von f zwischen a und b
oberhalb von g, so gilt für den Flächeninhalt A der von beiden Graphen über dem Intervall
[a; b] eingeschlossenen Fläche
b
A   ( f ( x)  g ( x))dx
a
Vorgehensweise:
1. Zuerst berechnet man die Schnittpunkte der beiden Funktion f und g.
2. Danach stellt man die entsprechenden Integrale mit den Integralgrenzen auf.
3. Zum Schluss stellt man die Grundintegrale auf und addiert die einzelnen Flächeninhalte.
7 Abschluss
Dies war nun der erste Teil der Serie „Einführung in die Integralrechnung“. Der zweite Teil
wird sich um die Stammfunktion drehen. Schon so viel vorweg: Mit der Stammfunktion
braucht man nicht mehr die Grundintegrale. Man kann also Integrale auf einer schnelleren Art
berechnen. Aber ich will nicht zu viel verraten. Einfach auf den zweiten Teil warten, der
schon in 2-3 Wochen erscheinen wird.
8 Quellenangabe
Ich habe mich sehr an mein wunderschönes, ausführliches und verständlich Schulbuch
gehalten. Hier zu kaufen:
Florian Modler