ntmueb6kanal

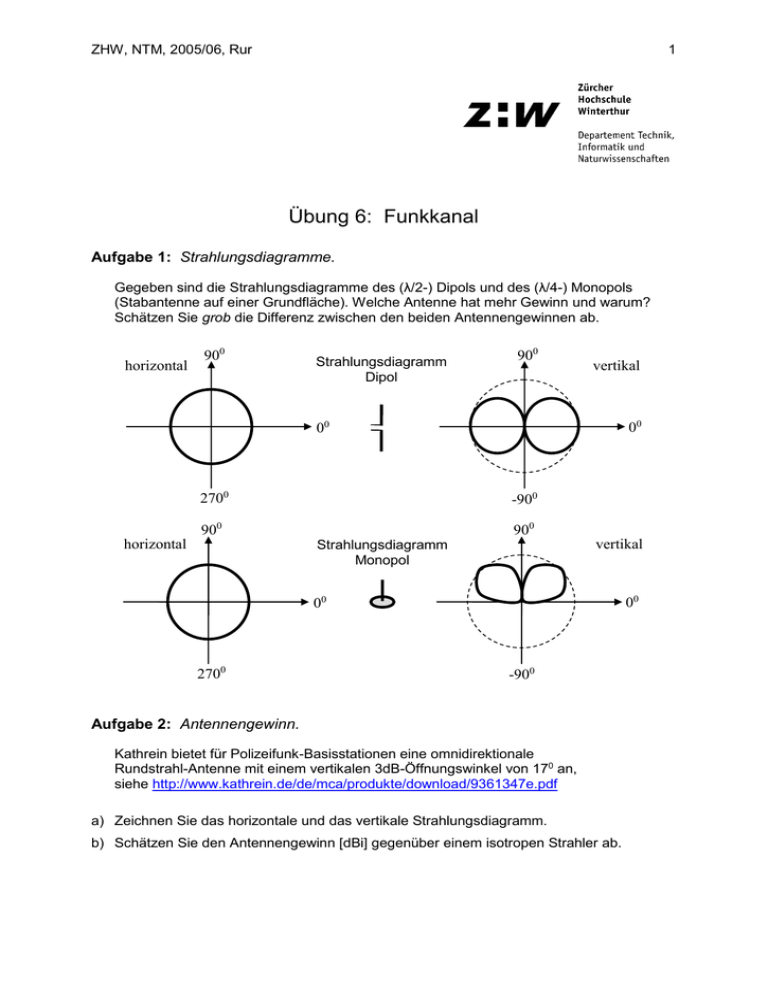
ZHW, NTM, 2005/06, Rur
1
Übung 6: Funkkanal
Aufgabe 1: Strahlungsdiagramme.
Gegeben sind die Strahlungsdiagramme des (λ/2-) Dipols und des (λ/4-) Monopols
(Stabantenne auf einer Grundfläche). Welche Antenne hat mehr Gewinn und warum?
Schätzen Sie grob die Differenz zwischen den beiden Antennengewinnen ab.
horizontal
900
Strahlungsdiagramm
Dipol
900
vertikal
00
00
2700
-900
900
900
horizontal
vertikal
Strahlungsdiagramm
Monopol
00
00
2700
-900
Aufgabe 2: Antennengewinn.
Kathrein bietet für Polizeifunk-Basisstationen eine omnidirektionale
Rundstrahl-Antenne mit einem vertikalen 3dB-Öffnungswinkel von 170 an,
siehe http://www.kathrein.de/de/mca/produkte/download/9361347e.pdf
a) Zeichnen Sie das horizontale und das vertikale Strahlungsdiagramm.
b) Schätzen Sie den Antennengewinn [dBi] gegenüber einem isotropen Strahler ab.
ZHW, NTM, 2005/06, Rur
2
Aufgabe 3: Freiraumausbreitung.
Quelle: Proakis, Salehi, „Grundlagen der Kommunikationstechnik“, Pearson, 2004.
Ein Satellit auf einer geostationären Bahn 36000 km über der Erdoberfläche strahlt eine
Leistung von 100 W aus. Die Sendeantenne hat einen Gewinn von 18 dB. Die Station
auf der Erde verwendet eine Parabolantenne mit einem Durchmesser von 3m. Die Übertragungsfrequenz beträgt 4 GHz. Bestimmen Sie die Empfangsleistung Pe [dBm].
Aufgabe 4: Mobilfunkausbreitung.
Betrachten Sie das (vereinfachte) Linkbudget für den Downlink eines Polizeifunksystems
bei 400 MHz für eine (inner)städtische Umgebung:
Basisstation (BS): abgestrahlte Leistung bzw. EIRP
42 dBm
max. Ausbreitungsdämpfung Au
118 dB
Abschattung bzw. Shadowing
Gebäudeverlust + Körperverlust
Mobilstation (MS): dynamische Empfindlichkeit
7 dB
28 dB
-111 dBm
a) Bestimmen Sie die maximale Reichweite Ru [km] zwischen BS und MS, wenn die BSHöhe hBS = 30 m und die MS-Höhe hMS = 1.5 m.
b) Bestimmen Sie die maximale Reichweite Rsu [km] zwischen BS und MS in einer Vorstadt,
wenn das Linkbudget oben weiter gilt und hBS und hMS gleich sind wie in Teilaufgabe a).
c) Wieviel mal mehr oder weniger BS braucht es zur Versorgung einer bestimmten Fläche F
in der (Innen) Stadt im Vergleich zur Vorstadt.
Aufgabe 5: Ausbreitung Mobilfunk.
In einem Mobilkommunikationssystem werden 2 verschiedene Mobilgeräte eingesetzt.
Das Mobilgerät A ist 3.5 dB empfindlicher als das Mobilgerät B. Wie viel weiter weg vom
Sender können Sie das Mobilgerät A einsetzen als das Mobilgerät B?
Hinweis: Für die Streckendämpfung dürfen Sie 35 dB pro Dekade annehmen.
Aufgabe 6: Uplink und Downlink Frequenzen im Mobilfunk (1).
Im Mobilfunk sind jeweils die Uplink-Frequenzbänder unterhalb der Downlink-Frequenzbänder angeordnet. Ein GSM-Handy z.B. sendet auf 200 kHz Kanälen im Bereich von
890-915 MHz (Uplink) und die Basisstation sendet auf 200 kHz Kanälen im Bereich von
935-960 MHz (Downlink). Erklären Sie bitte warum.
Aufgabe 7: Uplink und Downlink Frequenzen im Mobilfunk (2).
Wenn man bei Mobilfunk-Basisstationen getrennte Antennen für Sender (Tx) und
Empfänger (Rx) einsetzt, dann platziert man normalerweise die Rx-Antenne höher
oben am Antennenmast als die Tx-Antenne. Erklären Sie bitte warum.
ZHW, NTM, 2005/06, Rur
3
Aufgabe 8: Mehrwegausbreitung.
Betrachten Sie die dargestellte Übertragung eines BP-Signals sBP(t) von der Basisstation
(BS) zur Mobilstation (MS) über 2 verschiedene Wege. Für die Distanzen gilt: d1=1 km
und d2=√2·d1. Und für den Abschwächungsfaktor auf dem längeren Pfad gilt: α2=0.8·α1.
Reflektor
d2, α2, τ2
d1, α1, τ1
BS
MS
a) Bestimmen Sie die relative Zeitverzögerung τ12 = τ2 - τ1 zwischen den beiden
Empfangssignalen bei der MS.
b) Bestimmen Sie das Empfangssignal y(t) bei der MS, wenn die BS das BP-Signal sBP(t)
sendet.
c) Bestimmen Sie analytisch das Betragsspektrum IH(f)I dieses Mehrwegkanals und
skizzieren Sie es. Wo treten Minima bzw. Maxima auf und wie gross sind sie?
d) Die BS sendet auf einer Trägerfrequenz f0 = 950 MHz. Bestimmen Sie IH(f0)Id1=1000m.
Die MS bewegt sich jetzt 0.3m nach rechts. Bestimmen Sie IH(f 0)Id1=1000.3m.
Vergleichen Sie IH(f0)Id1=1000m und IH(f0)Id1=1000.3m. Was schliessen Sie daraus?
e) Betrachten Sie ein Nachrichtensystem mit grosser Bandbreite B=5/τ12 und eines mit
kleiner Bandbreite B=1/(5·τ12) und erklären Sie das unterschiedliche Verhalten in obiger
Mehrwegumgebung.
ZHW, NTM, 2005/06, Rur
4
Musterlösung
Aufgabe 1
Der Antennengewinn des Monopols ist grösser als der Antennengewinn des Dipols,
weil die gleiche Sendeleistung in einen kleineren Raumwinkel abgestrahlt wird.
Das Verhältnis der Abstrahl-Raumwinkel ist ca. 2:1, d.h. der Antennengewinn GM des
Monopols ist ca. 3 dB grösser als der Antennengewinn des Dipols GD. Die genauen
Werte sind: GM = 4.0 dBi, GD = 2.14 dBi.
Aufgabe 2
a) Strahlungsdiagramm
horizontal
900
900
vertikal
-3 dB
170
00
0
0
2700
-900
b) G entspricht approximativ dem Flächenverhältnis der Oberfläche der Einheitskugel (4π)
zur Oberfläche A der „Antennenöffnung“.
Approximation von A: A ≈ 2π·2x, wobei x = sin(8.50), siehe unten.
1
8.50
A
x
x
G ≈ 10·log10(4π / 2π·2·sin(8.50)) = 10·log10(1/sin(2π·8.5/360) = 8.3 dBi
einfacher: G ≈ 10·log10(4π / (2π·2·(8.50)rad)) = -10·log10((8.50)rad)
Tatsächlich hat die Kathrein-Antenne einen Gewinn von 7.5 dBi,
siehe http://www.kathrein.de/de/mca/produkte/download/9361347e.pdf
ZHW, NTM, 2005/06, Rur
5
Aufgabe 3
Sendeleistung Satellit:
Ps = 100 W bzw. 50 dBm
Gewinn Sendeantenne:
Gs = 18 dB
Freiraumdämpfung:
Af = 32.4 + 20·log10(4000) + 20·log10(36000) = 195.6 dB
Gewinn Empfangsantenne:
Ge = 10·log10(4π·Ae / λ2) = 40 dB
wobei λ = 0.075 m, Ae = (2/3)·π·r2 = 4.7 m2 und r=1.5 m
Empfangsleistung:
Pe = 50 dBm + 18 dB -195.6 dB + 40 dB = -87.6 dBm
Aufgabe 4
Allgemeines Ausbreitungsmodell: Au [dB] = a + b·log10(R [km])
a) Okumura-Hata-Modell: Au = 118 dB, a = 117.21 dB, b = 35.22 dB
=> Reichweite: Ru ≈ 1.05 km
b) Okumura-Hata-Modell: Asu = 118 dB, a = 109.14 dB, b = 35.22 dB
=> Reichweite: Ru ≈ 1.78 km
c) Anzahl BS in der Stadt: Nu ≈ F / (π·Ru2)
Anzahl BS in der Vorstadt: Nsu ≈ F / (π·Rsu2)
Es braucht ca. Nu / Nsu = Rsu2 / Ru2 = 2.8 mal mehr BS zur Versorgung einer Fläche F in
der Innenstadt gegenüber der Vorstadt.
Aufgabe 5
Die Differenz der Streckendämpfung in Funktion der maximalen Abstände RA und RB
beträgt: ΔA = 35·log10(RA/RB) = 3.5 => RA/RB = 103.5/35 = 100.1 = 1.26
Mit dem Mobilgerät A kann man sich also im Mittel 1.26 mal weiter weg von der
Basisstation entfernen als mit dem Mobilgerät B.
Aufgabe 6
Der Uplink vom Mobil zur Basisstation ist kritischer als der Downlink von der Basisstation
zum Mobil, weil die Sendeleistung im Mobil kleiner ist als in der Basisstation. Deshalb
teilt man dem Mobil die tiefere Sendefrequenz mit der grösseren Reichweite bzw. der
kleineren Streckendämpfung zu als der Basisstation, vgl. z.B. auch Okumura-HataAusbreitungsmodell.
Aufgabe 7
Der Uplink vom Mobil zur Basisstation ist kritischer als der Downlink von der Basisstation
zum Mobil, weil die Sendeleistung im Mobile kleiner ist als in der Basisstation. Deshalb
gibt man der Uplink-Empfangsantenne den besseren bzw. den höher gelegenen Antennenplatz, so dass die Streckendämpfung im Uplink kleiner ist als im Downlink, vgl. z.B.
auch Okumura-Hata-Ausbreitungsmodell.
ZHW, NTM, 2005/06, Rur
6
Aufgabe 8
a) τ12 = τ2 - τ1 = (d2-d1) / c = 1.381 μs
b) y(t) = α1·sBP(t-τ1) + α2·sBP(t-τ2)
c) Für die Übertragungsfunktion H(f) gilt: H(f) = Y(f) / SBP(f).
Mit der Fouriertransformation findet man: Y(f) = α1·SBP(f)·e-jφ1 + α2·SBP(f)·e-jφ2
wobei φ1=2πf·τ1 und φ2=2πf·τ2
Für das Betragsspektrum gilt: IH(f)I = α1·I 1+0.8·e-j2πf·τ12 I
=> periodisch, Maxima bzw. Minima im Abstand Δf = 1/τ12 = 724 kHz
=> max IH(f)I = 1.8·α1, min IH(f)I = 0.2·α1
d) Fall d1 = 1000 m: τ12 = 1.380711874576984 μs => IH(f0)I / α1 = 0.9618
Fall d1 = 1000.3 m: τ12 = 1.381126088139357 μs => IH(f0)I / α1 = 1.7575
Schon geringe Distanzverschiebungen in der Grössenordnung von einer Wellenlänge λ
verursachen Phasenveränderungen in der Grössenordnung von 2π und ändern damit die
Charakteristik der Mehrwegausbreitung wesentlich.
e) Das Nachrichtensystem mit der kleinen Bandbreite kann die beiden Signalwege zeitlich
nicht auflösen (τ12 = 0.2·Symboldauer). Folglich erscheint der Kanal als Einwegkanal mit
starkem Fading.
Das Nachrichtensystem mit der grossen Bandbreite kann die beiden Signalwege zeitlich
auflösen (τ12 = 5·Symboldauer). Es kommt zwar zu Intersymbol-Interferenz (ISI). Mit geeigneten Empfangsstrukturen können die beiden Signalanteile aber phasengerecht
aufsummiert werden (Diversity).