Daten - Schulbuchzentrum Online

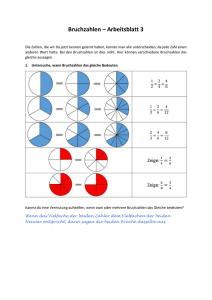
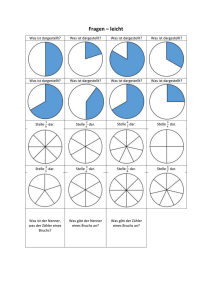
Von den Rahmenvorgaben des Lehrplans zum Schulcurriculum
Anregungen für Mathematik in der Realschule plus in Rheinland-Pfalz auf der Grundlage von Sekundo 6 (ISBN 978-3-507-84872-6)
Der Stoffverteilungsplan geht von folgenden Voraussetzungen aus:
 Es werden im 6. Schuljahr 4 Wochenstunden Mathematik unterrichtet. Daraus ergeben sich real ca. 150 Unterrichtsstunden pro Schuljahr
 Der Band 6 des Unterrichtswerkes „Sekundo“ wird „Seite für Seite“ abgearbeitet (aber nicht immer „Aufgabe für „Aufgabe“). Für das Notieren von
Modifikationen und anderen, auch schulspezifischen Schwerpunktsetzungen ist die letzte Spalte des Stoffverteilungsplans gedacht.
 Die jeweils angegebene Zahl von Unterrichtsstunden für die einzelnen Lerneinheiten ist nur als grobe Orientierungshilfe zu verstehen.
+ kennzeichnet Zusatzangebote (Additum) und Angebote zur Leistungs-Förderung
Inhalte und Ziele von Sekundo Band 6
(ISBN: 978-3-507-84872-6)
Stunden /
Seiten im
Buch
1. Kapitel: Zahlen, Größen und Teilbarkeit
16 Stunden
Natürliche Zahlen darstellen
6–9
- Große natürliche Zahlen lesen und schreiben
- Aufbau und Vorteile eines Stellenwertsystems angeben
- Natürliche Zahlen ordnen, runden und veranschaulichen
- Fachbegriffe: Natürliche Zahl, Stellenwert,
Stellenwertsystem, Stellenwerttafel
Wiederholen, Vertiefen, Vernetzen und
Weiterführen von Inhalten der 5. Jahrgangstufe
 mit natürlichen Zahlen und Größen operieren:
Grundrechenarten, Runden,
Überschlagsrechnen
 Darstellen von Zahlen und Größen am
Zahlenstrahl und im Diagramm
 Mit ganzen Zahlen in Anwendungen und
formal rechnen
 Darstellen von Figuren mit Koordinaten
(Zahlenpaaren) im Gitternetz
(1. Quadrant im Koordinatensystem)
 Begriffe (gemeinsame) Teiler, Vielfache und
Primzahl erarbeiten und sachorientiert
anwenden
 Teilbarkeitsregeln entdecken und anwenden
Leitideen und Inhalte gemäß dem Lehrplan 2007
Eigene Bemerkungen
10
Rechnen mit natürlichen Zahlen
11 – 14
15
16 – 18
19 – 20
- Im Kopf rechnen
- Schriftliche Rechenverfahren verstehen, ausführen und
anwenden
- Überschlagsrechnungen durchführen
- Teilbarkeitsregeln für 2,5,10,4,3,9
- Primzahlen und deren Eigenschaften angeben
- Teilbarkeitsregeln begründen
- Fachbegriffe: Teiler, Vielfache, Primzahl, Quersumme
Stoffverteilungsplan Sekundo Mathematik, Klasse 6, Realschule plus Rheinland-Pfalz
© 2011 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig
1

Formale und reale Anwendungen der
Teilbarkeitslehre in einfachen und komplexen
Problemen (Projektseite: Seriennummern mit
Prüfziffern)
 Lösen von Zuordnungsproblemen mit
rechnerischen und grafischen Methoden –
Zweisatz, Dreisatz bzw. KoordinatenDarstellung – Vermischte Aufgaben
 Kompetenzen durch Testen, Üben,
Vergleichen (TÜV) und in
Diagnosetest anwenden und sichern
Anmerkung:
Im Diagnosetest dienen die „Grundaufgaben“ zur
Sicherung von „Basis-Kompetenzen /
Minimalstandards“.
21 – 22
23 – 26
Ganze Zahlen darstellen
- Zahlen mit Vorzeichen im jeweiligen Sachzusammenhang
interpretieren
- Ganze Zahlen ordnen
- Den Zahlbereich erweitern
- Daten visualisieren
- Fachbegriffe: Ganze Zahl, Vorzeichen
27 – 28
Rechnen mit Ganzen Zahlen
- Sachaufgaben über Zustandsänderungen lösen
- einfache Terme auswerten und strukturieren
- einfache Gleichungen lösen
Formen und Beziehungen in Raum und Ebene
- Koordinatensystem verwenden
2. Kapitel: Brüche und Dezimalbrüche (1)
18 Stunden
Bruchzahlen darstellen

29 - 31
- Grundvorstellungen weiterentwickeln
° Maßzahl
° Operator
- Grundaufgaben der Bruchrechnung lösen
- Bruchzahlen auf verschiedene Arten schreiben
° Bruchschreibweise
° Dezimalschreibweise
- Bruchzahlen vergleichen und ordnen
° gemischte Zahlen
- Fachbegriffe: Zähler, Nenner, gemischte Zahl,
Dezimalbruch





Stammbrüche in Darstellungen (Bild, Grafik,
Text) erkennen und Anteile von Größen
bestimmen
Bruch-Begriff und Bruch-Darstellung
erarbeiten und Bruchteile von Größen
ermitteln
Bruchteile von (Maß-)Zahlen als Darstellung
von Rechen-Ergebnissen (Division)
interpretieren und bestimmen
Addieren und Subtrahieren von Brüchen mit
gleichem Nenner
BLEIB FIT: Grundwissen wiederholen
Dezimalbrüche darstellen (Stellenwerttafel,
Zahlenstrahl), ordnen und runden
32 - 34
34 – 36
37 – 39
40
41 – 44
Stoffverteilungsplan Sekundo Mathematik, Klasse 6, Realschule plus Rheinland-Pfalz
© 2011 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig
2



Addieren und Subtrahieren von
Dezimalbrüchen
Informationen aus Texten, Bildern und
Tabellen entnehmen und damit
anwendungsorientierte Aufgaben lösen
TÜV und Diagnosetest
45 – 47
Rechnen mit Bruchzahlen
48 – 50
- Bruchzahlen addieren und subtrahieren
° Brüche
° Dezimalbrüche
- Rechenverfahren in Sachsituationen anwenden
° Rechnen mit Größen
51 – 52
3. Kapitel: Kreise, Winkel, Symmetrien
15 Stunden
Grundprinzip Messen

53 - 55
56 - 57
- Das Grundprinzip des Messens als vergleichen mit einer
Einheit auf die Größen anwenden
° Winkelmaß
- Fachbegriffe: Winkel, Winkelmaß
58 -60
Rechnen mit Größen
61
- Mit Größen in Sachsituationen rechnen
° Maßstab
° Formeln anwenden








Kreise zeichnen, Radius und Durchmesser
messen und berechnen in Mustern und SachAnwendungen
Winkelgrößen und Winkelarten erkennen und
charakterisieren
Winkel messen und zeichnen –
Anwendungen
Projekt: Segeltörn
Informationen aus Texten und Landkarte
entnehmen, Modellieren und Probleme lösen
+ Wissen – Anwenden – Vernetzen (WAV)
Komplexe Themen zum Modellieren und
Problemlösen zu verschiedenen Leitideen
BLEIB FIT: Grundwissen wiederholen
Erzeugen von symmetrischen Mustern durch
Falten, Schneiden und Zeichnen
Achsen-, Punkt- und Drehsymmetrien
erkunden, beschreiben und konstruieren
TÜV und Diagnosetest
62 - 63
64
65
66 – 72
73 – 74
Symmetrische Figuren
- Achsensymmetrie
° Symmetrieachsen durch Falten und Zeichnen
bestimmen
° achsensymmetrische Figuren erzeugen
- Drehsymmetrie
° drehsymmetrische Figuren erkennen
° Drehzentrum und Drehwinkel angeben
° Einfache Figuren drehen
- Winkelbegriff
° Schenkel, Scheitelpunkt
° Winkel schätzen, messen, zeichnen
° Winkel klassifizieren
- Kreise zeichnen
Stoffverteilungsplan Sekundo Mathematik, Klasse 6, Realschule plus Rheinland-Pfalz
© 2011 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig
3
- Mittelpunkt, Radius, Durchmesser
- Fachbegriffe: Symmetrisch, achsensymmetrisch,
Symmetrieachse, verschiebungssymmetrisch,
drehsymmetrisch, Drehzentrum, Drehwinkel, Abstand,
Winkel, Schenkel, Scheitelpunkt, Mittelpunkt, Radius,
Durchmesser
4. Kapitel: Brüche und Dezimalbrüche (2)
26 Stunden
Bruchzahlen darstellen

75- 81
- Grundvorstellungen weiterentwickeln
° Maßzahl
° Operator
- Bruchzahlen auf verschiedene Arten schreiben
° Bruchschreibweise
° Dezimalschreibweise
° Prozentschreibweise








Brüche mit natürlichen Zahlen multiplizieren
und durch natürliche Zahlen dividieren
(einfache Brüche und Zahlen ohne
numerische Last) mit Anwendungen in
Sachsituationen
Dezimalbrüche vervielfachen, schriftliche
Multiplikation mit einfachen Zahlen
Computer-Tabellen zu Sachbereichen lesen
und zum Problemlösen nutzen
BLEIB FIT: Wiederholung von Grundwissen
Division von Dezimalbrüchen durch
einstellige natürliche Zahlen
Brüche (mit kleinen Nenner) in
Dezimalbrüche umwandeln;
+ * periodische Dezimalbrüche
Informationen aus Texten, Bildern, Grafiken
und Landkarten entnehmen zum Modellieren
und Problemlösen nutzen
Zusammenhang zwischen Brüchen,
Dezimalbrüchen und Prozentschreibweise
erkennen und nutzen beim Kopfrechnen für
Anteile von Größen
TÜV und Diagnosetest
82 - 83
84 – 85
Rechnen mit Bruchzahlen
86
87 -88
89
90 – 92
- Bruchzahlen multiplizieren und dividieren
° Brüche
° Dezimalbrüche
- Rechenverfahren in Sachsituationen anwenden
° Rechnen mit Größen
- Einfache Terme auswerten und strukturieren
- Einfache Gleichungen lösen
93 – 94
95 - 96
* Anmerkung: LVL-Aufgaben zu
„periodischen“ Dezimalbrüchen dienen als
Angebot für leistungsstarke Schülerinnen
und Schüler
Stoffverteilungsplan Sekundo Mathematik, Klasse 6, Realschule plus Rheinland-Pfalz
© 2011 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig
4
5.Kapitel: Flächen- und Rauminhalt
20 Stunden
Grundprinzip Messen

97 - 100
- Das Grundprinzip des Messens als vergleichen mit einer
Einheit auf die Größen anwenden
° Flächeninhalt
° Volumen
- Formeln Herleiten
° Umfang und Flächeninhalts des Rechtecks
° Volumen und Oberflächeninhalt des Quaders
- Fachbegriffe: Länge, Umfang, Flächeninhalt,
Oberflächeninhalt, Rauminhalt/ Volumen









Flächeninhalt und Umfang des Rechtecks –
Formeln erarbeiten, Maßeinheiten
wiederholen, inner- und außermathematische
Anwendungen
Projekte für Partner- und Gruppenarbeit zu
Umfang und Flächeninhalt
zusammengesetzter Flächen und in
Realsituationen
BLEIB FIT: Wiederholung von Grundwissen
Schrägbilder zeichnen, Würfel- und
Quadernetzen erkennen und zeichnen
Oberfläche von Quadern berechnen
Rauminhalt messen und vergleichen ,
sinnvolle Maßeinheiten verwenden, Volumen
von Quadern bestimmen
+ Projekte, auch WAV, zum Modellieren und
Problemlösen
Themen: Regenmengen, Ausflug,
Einladungen, Pakete, Schatzsuche
Maßeinheit für große Volumen erarbeiten und
anwenden
Projekte für Einzel- und Partnerarbeit
TÜV und Diagnosetest
101 - 105
106
107 -110
Rechnen mit Größen
111
112 - 116
117 – 119
120 - 121
122 – 124
125 – 126
- Dieselbe Größe in verschieden Einheiten angeben
° Umrechnungszahlen
° Vorsilben: Milli-, Zenti-, Dezi-, Kilo° Kommaschreibweise
- Mit Größen in Sachsituationen rechnen
° angemessen runden
° Maßstab
° Formeln anwenden
- Fachbegriffe: Milli-, Zenti-, Dezi-, KiloFormen und Beziehungen in Raum und Ebene
- Körper in der Umwelt
Würfel, Quader
- Vierecke
Quadrat und Rechtecke beschreiben, zeichnen und
skizzieren
- Orientierungsmodelle
Beziehungen zwischen Netzen und Körpern beschreiben
Kanten- und Flächenmodelle (Netze) herstellen und
zeichnen
Quader und Würfel durch Schrägbilder darstellen
- Fachbegriffe: Würfel, Quader, Ecke, Kante, Fläche,
Netzt, Körper, Schrägbild
Stoffverteilungsplan Sekundo Mathematik, Klasse 6, Realschule plus Rheinland-Pfalz
© 2011 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig
5
6. Kapitel: Brüche und Dezimalbrüche (3)
25 Stunden
Bruchzahlen darstellen

127 -131
- Grundvorstellungen weiterentwickeln
° Maßzahl
° Operator
- Bruchzahlen auf verschiedene Arten schreiben
° Bruchschreibweise
° Dezimalschreibweise
° Prozentschreibweise
- Bruchzahlen vergleichen und ordnen
° Größenvorstellung nutzen
° Brüche erweiten und kürzen
° Unterschied Bruch - Bruchzahl
- Fachbegriffe: erweitern, kürzen, Bruchzahl









Unterteilungen von Figuren verfeinern und
vergröbern – Erarbeiten des Erweiterns und
Kürzens, formale Übungen
Entdecken von Vergleichsmethoden für
Anteile und Regeln zum Vergleichen von
Brüchen
Brüche, Dezimalbrüche und
Prozentschreibweise als verschiedene
Darstellungen von Zahlen kennen
Brüche / Bruchzahlen am Zahlenstrahl
darstellen
BLEIB FIT: Wiederholung von Grundwissen
Erarbeiten der Regeln für Addition und
Subtraktion, regelgebundenes Operieren mit
Brüchen
Arbeiten mit Brüchen und Dezimalbrüchen an
einem Realmodell (Bruch-Streifen) und
formales, vorteilhaftes Addieren und
Subtrahieren
Projekt für Einzel- und Partnerarbeit zum
Modellieren, Problemlösen und Präsentieren
Thema zum Üben, Entdecken, Begründen:
+Rechnen wie die alten Ägypter
TÜV und Diagnosetest
132 - 133
134 - 135
136 - 137
138
139 – 142
143-145
146 – 147
Rechnen mit Bruchzahlen
- Bruchzahlen addieren und subtrahieren
° Brüche
- Rechenverfahren in Sachsituationen anwenden
° Rechnen mit Größen
- Einfache Terme auswerten und strukturieren
- Einfache Gleichungen lösen
148
149 - 150
7. Kapitel: Daten und Zufall
18 Stunden
Daten
 Daten aus dem Schüleralltag in Listen
erfassen, den arithmetischen Mittelwert
(Durchschnitt) und die Spannweite berechnen
 + Median (Zentralwert) einer geordneten
Rangliste für Daten berechnen und
interpretieren
151 - 153
- Datenerhebungen planen, durchführen und auswerten
° absolute und relative Häufigkeiten
° arithmetisches Mittel
° grafische Darstellungen und deren Aussagekraft
- Informationen aus Datendarstellungen entnehmen und
interpretieren
154
Stoffverteilungsplan Sekundo Mathematik, Klasse 6, Realschule plus Rheinland-Pfalz
© 2011 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig
6
 Häufigkeiten (absolute und relative) für den
Vergleich von Datenlisten berechnen und
interpretieren
 Säulen und Streifendiagramme
interpretieren und zeichnen, Daten in Tabellen
und Grafiken interpretieren; Anregungen für
Gruppenarbeit
 + Experimentieren mit Zufallsversuchen –
Die Würfel fallen
 + Präzisierung des Begriffs
Wahrscheinlichkeit
 BLEIB FIT: Wiederholung von Grundwissen
 + Wissen – Anwenden - Vernetzen (WAV)
Komplexe Themen zum Modellieren und
Problemlösen zu verschiedenen Leitideen
 Projekte für Einzel- und Partnerarbeit zum
Modellieren, Problemlösen und Präsentieren
 TÜV und Diagnosetest
155 – 156
8. Kapitel: Brüche und Dezimalbrüche (4)
12 Stunden
Rechnen mit Bruchzahlen

171 - 172
- Bruchzahlen multiplizieren und dividieren
° Brüche
° Dezimalbrüche
- Kehrbruch/ Kehrwert
° Brüche
- Rechenverfahren in Sachsituationen anwenden
° Rechnen mit Größenvorstellung
° Überschlagsrechnungen durchführen
- Fachbegriffe: Kehrbruch/ Kehrwert





Bildaufgaben und Projekt zur Vorbereitung
und Begründung der Multiplikations-Regel für
Brüche*
Regel-Anwendungen
Projekt zur Erarbeitung und Begründung der
Divisions-Regel für Brüche*
Regel zur Bruchdivision festigen durch
formale und sachbezogene Übungen*
BLEIB FIT: Wiederholung von Grundwissen
Multiplikation und Division von
Dezimalbrüchen – Kopfrechnen, Runden,
Überschlagen, schriftliche Verfahren und
Rechenproben
- Fachbegriffe: Häufigkeit, arithmetisches Mittel
157
158 - 159
160
161
162-163
164 – 167
169 - 170
173
174
175 -177
178
179 – 186
Stoffverteilungsplan Sekundo Mathematik, Klasse 6, Realschule plus Rheinland-Pfalz
© 2011 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig
7



Informationen aus Texten, Bildern und
Tabellen entnehmen, modellieren und
Problemlösungen finden
Projekte für Einzel- und Partnerarbeit zum
Modellieren, Problemlösen und Präsentieren
TÜV und Diagnosetest
187
188 - 189
190 – 191
* Anmerkung: Diese Projektseiten fördern das
selbstentdeckende Lernen
Training Basiswissen und Diagnosearbeiten
Aufgaben zur Diagnose des Leistungsstands am
Ende des Schuljahrs
192 - 194
Übungen mit Selbstkontrolle und regelmäßige
Lernstandserhebungen kontrollieren die Effektivität des
Unterrichts, geben Lehrenden und Lernenden
Rückmeldungen und bereiten auf (landesweite)
Lernstandserhebungen vor.
Stoffverteilungsplan Sekundo Mathematik, Klasse 6, Realschule plus Rheinland-Pfalz
© 2011 Bildungshaus Schulbuchverlage Westermann Schroedel Diesterweg Schöningh Winklers GmbH, Braunschweig
8