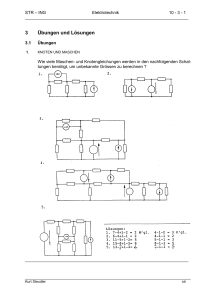
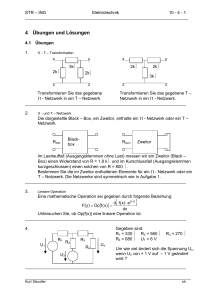
STR-ING ELEKTROTECHNIK 97 - 1 ______________________________________________________________________ 97 KOMPLEXE RECHNUNG III (Funktionen, SMITH - Chart) 97.1 Funktionen Die komplexe Zahl z sei ein Element der Menge A: z A und die Menge A sei eine Teilmenge der Menge der komplexen Zahlen: A . Der komplexen Zahl z werde durch eine Abbildungsvorschrift f die komplexe Zahl w zugeordnet. Die komplexe Zahl w (das Bild von z) sei Element einer Menge B: w B und die Menge B eine Teilmenge der komplexen Zahlen: B . f z w A Fig. 97-1 B Abbildung z in w Begriffe und Konventionen Die Abbildungsvorschrift f bezeichnen wir als komplexe Funktion. Die Menge A wird als Urmenge oder Definitionsbereich bezeichnet. Die Menge B bezeichnen wir als Bildmenge oder Wertebereich. In w = f(z) bedeuten z das Argument der Funktion f und w den Wert der Funktion f zum Argument z. Die komplexe Zahl z = a + j⋅b wird durch f abgebildet in die komplexe Zahl w = u + j⋅v. Für grafische Darstellungen werden zwei GAUSS’ sche - Zahlenebenen verwendet. In der z-Ebene finden wir die Urmenge (zum Beispiel die Menge aller Punkte eines Kreises │Z│⋅ e jωt ) und in der w-Ebene die Bildmenge (zum Beispiel die Menge aller Punkte eines Tragflügelprofils). Beispiel w = f(z) = 1 1 ⋅ z + 2 z _____________________________________________________________________ Kurt Steudler 97 - 1 str STR-ING ELEKTROTECHNIK 97 - 2 ______________________________________________________________________ 1j jb Im Im jv 1j z2 z1 1 z1 = 1 w2 a Re 1 w1 = 1 Re w2 = 0,75 + j z2 = 1 + j Fig. 97-2 u w1 Beispiel zu Abbildung z - w Die Abbildung w = f(z) = j⋅α 1 1 ⋅ z + , angewendet auf den Kreis 2 z z = -0,5+j + 1,803⋅e , zeigt ein Flügelprofil: z - Ebene 4 2 2 1 0 0 2 Fig. 97-3 w - Ebene 4 2 0 1 2 2 1 0 1 Flügelprofil 97.2 Die Umkehrfunktion Jene Abbildung, die dem Bild einer Funktion f(z) wieder die Urbilder zuordnet, -1 bezeichnen wir als Umkehrfunktion f (z). f z w A Fig. 97-4 f-1 B Umkehrfunktion _____________________________________________________________________ Kurt Steudler 97 - 2 str STR-ING ELEKTROTECHNIK 97 - 3 ______________________________________________________________________ -1 Funktion f(z) Umkehrfunktion f (w) a) w=z-a b) w = a⋅z c) d) w=e w = cos(z) z=w+a w z= a z = ln(w) z = arccos(w) z Beispiel: Berechnung von w = arccos(z) Aufgelöst nach z wird 1 und mit der Euler-Relation j⋅w Mit 2⋅e w = arccos(z) z = cos(w) jw + -jw e z= e 2 j⋅w 2⋅z⋅e multipliziert wird j⋅w j⋅2⋅w =e +1 2 und durch Substitution r=e r - 2⋅z⋅r + 1 = 0 Daraus wird r=e und durch logarithmieren ln(r) = j⋅w = ln( z ± z 2 - 1 ) Womit j⋅w 2 = z ± z2 - 1 w = -j⋅ln( z ± z 2 - 1 ) ___________________ 97.3 Transformationen z = x + j⋅y sei die kartesische Darstellung des Punktes z in der z-Ebene. Diesem Punkt wird durch die Abbildungsvorschrift f ein Punkt w in der w-Ebene zugeordnet. Die kartesische Darstellung von w sei angegeben mit w = u + j⋅v. Damit gilt: u + j⋅v = f(x + j⋅y) Vergleichen wir die Realteile und die Imaginärteile beider Seiten, erhalten wir u = (x,y) und v = v(x,y) u = u(x,y) und v = v(x,y) nennen wir Transformation. 1 2 Umformung aus (95.5). Es gelten folgende Beziehungen: e jα - e-jα e jα + e-jα . sin(α) = und cos(α) = 2⋅ j 2 Wenn z gegeben ist, lässt sich der Ausdruck weiter verarbeiten nach den Regeln in 95 und 96. _____________________________________________________________________ Kurt Steudler 97 - 3 str STR-ING ELEKTROTECHNIK 97 - 4 ______________________________________________________________________ Beispiel 1 : 2 Gegeben sei die Abbildungsvorschrift w = f(z) = z . Damit wird z = x + j⋅y abgebildet in 2 2 2 2 w = u + j⋅v = z = (x + j⋅y) = (x - y ) + j⋅2xy Daraus lässt sich die Transformation ablesen: 2 2 u = u(x,y) = (x - y ) und v = v(x,y) = j⋅2xy Anwendung: In der w-Ebene seien zwei spezielle Geraden gegeben, nämlich einerseits die Gerade u = 1 und andererseits die Gerade v = 1. Frage: wie sehen die Urbilder der beiden Geraden in der z-Ebene aus ? 2 2 Aus u = 1 = x - y und v = 1 = j⋅2xy erhalten wir x2 - 1 y= und y= 1 2x Die beiden Urbilder stellen in der z-Ebene demnach Hyperbeln dar. z - Ebene w - Ebene 2 2 1 1 0 0 1 2 2 Fig. 97-5 1 0 1 2 1 1 0 1 Hyperbel 2 Durch die Transformation w = z werden Hyperbeln in Geraden abgebildet. 2 Die Transformation w = z liefert eine Koordinatentransformation von kartesischen auf hyperbolische Koordinaten. _____________________________________________________________________ Kurt Steudler 97 - 4 str 2 STR-ING ELEKTROTECHNIK 97 - 5 ______________________________________________________________________ Beispiel 2 : Gegeben sei r = e jα = cos(α) + j⋅sin(α). Frage: was für eine Transformation liefert die lineare Abbildung w = r ⋅ z ? (z = x + j⋅y) = r⋅z = [cos(α) + j⋅sin(α)]⋅(x + j⋅y) = [x⋅cos(α) - y⋅sin(α)] + j⋅[x⋅sin(α) + y⋅cos(α)] = u + j⋅v Für x und y lesen wir folgende Transformationen ab: w u = u(x,y) = x⋅cos(α) - y⋅sin(α) und v = v(x,y) = x⋅sin(α) + y⋅cos(α) Sind x und y die kartesischen Koordinaten eines Punktes, dann sind u und v die Koordinaten desselben Punktes in einem um den Winkel α gedrehten Koordinatensystem. Die Transformation w = r⋅z bewirkt eine Drehung des Koordinatensystems. Transformationen dienen der einfacheren Handhabung in der Bildebene gegebener Problemstellungen in der Urebene 97.4 Die SMITH - Chart Aus der Transformation w = 3 4 z -1 entsteht das SMITH - Diagramm oder die z +1 SMITH - Chart. , Die Besonderheit dieser Transformation liegt darin, dass die ganze rechte Halbebene der GAUSS’ schen Zahlenebene (Re > 0) auf eine Kreisfläche mit dem 5 Radius 1 abgebildet wird. Normierte Impedanzen, Spannungsverhältnisse, Reflexionskoeffizienten und so weiter weisen in ihrer komplexen Darstellung einen positiven Realteil auf; sie bewegen sich in ihrer Frequenzabhängigkeit in der rechten Hälfte der GAUSS’ schen Ebene. Aus diesem Grund ist die Transformation gut geeignet für die Lösung von Problemen in elektrotechnischen und elektronischen Anwendungen. Die Abbildung von Geraden z = a ± j⋅Ω mit a ≥ 0, 0 ≤ Ω < ∞ 3 4 5 SMITH P.H., beschreibt 1939 diese Transformation erstmals im Artikel «Transmission Line Calculator» in ELECTRONICS Nr.1 Das SMITH - Diagramm gehört zum Handwerkzeug in der Elektronik. Netzwerk-Analysatoren arbeiten auf der Basis der SMITH - Chart; ohne Kenntnis der Transformation nach SMITH lassen sich diese Instrumente nicht einsetzen Die SMITH - Chart holt die Unendlichkeit in einen endlichen Kreis. _____________________________________________________________________ Kurt Steudler 97 - 5 str STR-ING ELEKTROTECHNIK 97 - 6 ______________________________________________________________________ Diese beliebigen Parallelen zur imaginären Achse, miteingeschlossen die imaginäre Achse selbst und mit dem Parameter a bilden sich folgendermassen ab w = z -1 a - 1± j ⋅ Ω = = u + j⋅v z +1 a + 1± j ⋅ Ω worin u = u(a,Ω) = v = v(a,Ω) = ± a2 - 1 + Ω 2 (a + 1)2 + Ω2 und 2⋅Ω (a + 1)2 + Ω 2 Für die imaginäre Achse selbst gilt a = 0. Damit bildet sich der Ursprung (Ω = 0) ab an den Ort -1 , 0. Für Ω → ∞ wird der Ort +1 , 0 erreicht. Für beliebige Ω liegen die abgebildeten Punkte auf einem Kreis mit dem Radius 1 und dem Zent6 rum im Ursprung des Koordinatensystems. Alle übrigen Parallelen zur imaginären Achse mit a > 0 bilden sich ebenfalls ab als Kreise, die durch +1 , 0 gehen, symmetrisch zur reellen Achse liegen und den Radius r = 1/(1+a) aufweisen. 2 1 1 0.5 0 0 1 2 Fig. 97-6 0.5 0.5 0 0.5 1 1.5 1 1 0.5 0 0.5 1 Smith – Chart 1 Die Abbildung von Geraden z = Ω ± j⋅b mit b ≥ 0, 0 ≤ Ω < ∞ Diese beliebigen Parallelen zur reellen Achse, miteingeschlossen die reelle Achse selbst und mit dem Parameter b bilden sich folgendermassen ab w 6 = z -1 Ω - 1± j ⋅ b = = u + j⋅v z +1 Ω + 1± j ⋅ b 2 2 Die Aussage ist beweisbar aus der Bedingung u + v = 1, die dann gelten muss. _____________________________________________________________________ Kurt Steudler 97 - 6 str STR-ING ELEKTROTECHNIK 97 - 7 ______________________________________________________________________ worin u = u(a,Ω) = v = v(a,Ω) = ± Ω 2 - 1 + b2 (Ω + 1)2 + b2 und 2⋅b (Ω + 1)2 + b2 Für die reelle Achse selbst gilt b = 0. Damit bildet sich der Ursprung (Ω = 0) ab an den Ort -1 , 0. Für Ω → ∞ wird der Ort +1 , 0 erreicht. Für beliebige Ω liegen die abgebildeten Punkte auf der reellen Achse an den Orten (Ω-1)/(Ω+1). Die Abbildung für Ω = 1 liegt im Ursprung des Koordinatensystems. Alle übrigen Parallelen zur reellen Achse mit b > 0 bilden sich ebenfalls ab als Kreisausschnitte, die in +1 , 0 enden und symmetrisch zur reellen Achse liegen. Mit b = 1 bilden sich Viertelkreise mit dem Radius 1, die in ±j , 0 beginnen und in +1 , 0 enden. 1 1 0 0 1 2 Fig. 97-7 0 0.5 1 1 1 0.5 0 0.5 1 Smith – Chart 2 Spezielle Eigenschaft: 1 Wird y = transformiert, entsteht ein Zeiger w(y), der zu w(z) um π (180°) gez dreht erscheint. 1 -1 z -1 y -1 7 = - w(z) == z w(y) = 1 y +1 z +1 +1 z 8 Für die praktische Anwendung wird spezielles Nomogramm-Papier hergestellt. Eine solche SMITH-Chart ist nachstehend gezeigt. 7 8 Diese Eigenschaft erlaubt es, den Kehrwert komplexer Grössen in der SMITH-Chart zu konstruieren. Die Konstruktion wird oft genutzt, um die Admitanz zu einer gegebenen Impedanz und umgekehrt aufzufinden. Ebenfalls Nomogramm - Papiere sind das einfachlogarithmische und das doppeltlogarithmische Papier. _____________________________________________________________________ Kurt Steudler 97 - 7 str STR-ING ELEKTROTECHNIK 97 - 8 ______________________________________________________________________ _____________________________________________________________________ Kurt Steudler 97 - 8 str STR-ING ELEKTROTECHNIK 97 - 9 ______________________________________________________________________ _____________________________________________________________________ Kurt Steudler 97 - 9 str STR-ING ELEKTROTECHNIK 97 - 10 ______________________________________________________________________ _____________________________________________________________________ Kurt Steudler 97 - 10 str