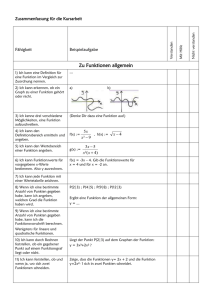
Beispiele zu linearen Funktionen

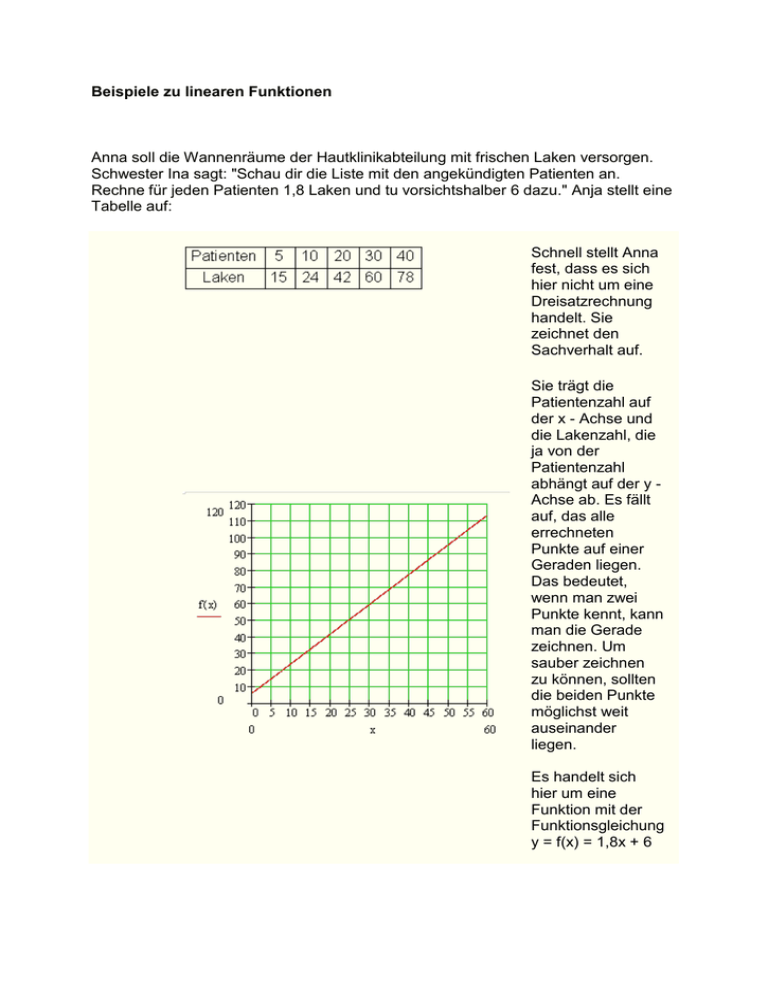
Beispiele zu linearen Funktionen
Anna soll die Wannenräume der Hautklinikabteilung mit frischen Laken versorgen.
Schwester Ina sagt: "Schau dir die Liste mit den angekündigten Patienten an.
Rechne für jeden Patienten 1,8 Laken und tu vorsichtshalber 6 dazu." Anja stellt eine
Tabelle auf:
Schnell stellt Anna
fest, dass es sich
hier nicht um eine
Dreisatzrechnung
handelt. Sie
zeichnet den
Sachverhalt auf.
Sie trägt die
Patientenzahl auf
der x - Achse und
die Lakenzahl, die
ja von der
Patientenzahl
abhängt auf der y Achse ab. Es fällt
auf, das alle
errechneten
Punkte auf einer
Geraden liegen.
Das bedeutet,
wenn man zwei
Punkte kennt, kann
man die Gerade
zeichnen. Um
sauber zeichnen
zu können, sollten
die beiden Punkte
möglichst weit
auseinander
liegen.
Es handelt sich
hier um eine
Funktion mit der
Funktionsgleichung
y = f(x) = 1,8x + 6
Besonderheit :
Aufgrund der Aufgabenstellung treten nur positive Werte in
den Koordinaten auf.
Eine Funktion heißt Lineare Funktion, wenn der Graph der
Funktion im rechtwinkligen Koordinatensystem eine Gerade
ist.
Sie heißt auch Funktion erster Ordnung oder Funktion ersten
Grades.
Die Funktionsgleichung lautet allgemein:
Definition
Der höchste Exponent von x ist 1, deshalb Funktion erster
Ordnung.
Beispiele von Graphen linearer Funktionen.
Bild 1
Bild 2
Bild 3
Bild 4
Gemeinsamkeiten:
Bild 1: Alle Graphen verlaufen durch den gemeinsamen
Koordinatenpunkt ( 0 | 1 ).
Bild 2. Alle Graphen sind zueinander parallel.
Bild 3: Alle Graphen verlaufen durch den gemeinsamen
Koordinatenpunkt ( 2 | 2 ).
Bild 4: Alle Graphen verlaufen durch den gemeinsamen
Koordinatenpunkt ( -3 | 0 ).
Eigenschaften linearer Funktionen
Weitere Eigenschaften linearer Funktionen werden nun
mathematisch betrachtet.
Arbeitsauftrag:
Die Graphen folgender linearer Funktionen sollen in ein
Koordinatensystem gezeichnet werden.
Stellen Sie eine Wertetabelle für x = - 5 , x
= 0 und x = 5 auf und zeichnen Sie die
Graphen.
Achsenteilung ( 1 cm = 1 ).
Vergleichen Sie mit den Graphen von Bild 1 bis Bild 4. Was
fällt Ihnen auf?
Wertetabelle:
Es besteht eine
Ähnlichkeit mit Bild 2.
Alle drei Graphen
verlaufen parallel
zueinander.
Der Schnittpunkt mit
der y - Achse entspricht
dem Wert von b aus
der Funktionsgleichung
y = f(x) = ax + b
Funktionenplotter
Überprüfen Sie die Graphen.
Merke
Der Graph der linearen Funktion y = f(x) = ax + b
schneidet die y - Achse im Punkt Py ( 0 | b ).
Arbeitsauftrag:
Die Graphen folgender linearer Funktionen sollen in ein
Koordinatensystem gezeichnet werden.
Stellen Sie eine Wertetabelle für x = - 5 , x
= 0 und x = 5 auf und zeichnen Sie die
Graphen.
Achsenteilung ( 1 cm = 1 ).
Wertetabelle:
Der Schnittpunkt mit
der y - Achse entspricht
dem Wert von b aus
der Funktionsgleichung
y = f(x) = ax + b
Alle drei Graphen
haben eine
unterschiedliche
Steigung.
Betrachtung der Steigung:
f(x) = 1x - 2 : wir gehen von x = -2 einen Schritt nach rechts,
der Graph steigt um 1
g(x) = 2x + 1 : wir gehen von x = 1 einen Schritt nach rechts,
der Graph steigt um 2
h(x) = -2x + 2 : wir gehen von x = 2 einen Schritt nach rechts,
der Graph fällt um 2
Die Steigung des Graphen hängt also unmittelbar mit dem
Faktor a aus f(x) = ax + b zusammen.
Funktionenplotter
Überprüfen Sie die Graphen.
Die Steigung
Was bedeutet das Verkehrszeichen 10% Steigung?
Prozent heißt von Hundert. Sinngemäß bedeutet 10%
Steigung, auf 100 m in waagerechter Richtung steigt die
Straße um 10 m oder auf 10 m steigt sie um 1 m.
Steigung
Die Steigung in einer linearen Funktion ist:
Das ist das Verhältnis von Gegenkathete zur Ankathete eines
beliebigen rechtwinkligen Dreiecks (Steigungsdreieck), dessen
Hypotenuse Teil des Funktionsgraphen ist.
Der Anstieg einer Geraden
Dieses Applet veranschaulicht in einem dynamischen
Diagramm den Anstieg als das Maß der "Steilheit" sowie den
Zusammenhang mit dem Strahlensatz.
Bemerkung:
Die Steigung einer linearen Funktion wird oft auch mit dem
Buchstaben m bezeichnet. ( z.B. y = mx + b )
Der Graph einer linearen Funktion hat überall die gleiche
Steigung.
Geraden mit der gleichen Steigung verlaufen parallel oder
sie überdecken sich.
Der Zähler des Bruches ist ein Maß für den Höhenanstieg,
der Nenner steht für Schritte nach rechts.
Beispiele:
Jetzt sind wir in der Lage, den Graphen einer linearen
Funktion direkt zu zeichnen, eine Wertetabelle ist nicht mehr
nötig.
Geraden erkennen
Es werden nacheinander mehrere Graphen linearer
Funktionen gezeigt, von denen die Funktionsgleichung zu
finden ist. Nach dem Durchlauf von 10 Aufgaben erfolgt eine
Benotung
Es ist nicht immer von Vorteil im Koordinatensystem für
beide Achsen den gleichen Maßstab zu nehmen. In der
Praxis werden oft unterschiedliche Größen dargestellt.
Beispiel:
Lea vergleicht vor dem Handykauf die Tarife unterschiedlicher
Anbieter.
Tarif A: Monatliche Grundgebühr 5 €, eine Minute telefonieren
0,25 €.
Tarif B: Monatliche Grundgebühr 10 €, eine Minute
telefonieren 0,20 €.
Welcher Tarif ist für sie der günstigste, wenn
a) ihr im Monat 50 € zur Verfügung stehen
b) sie nicht mehr als 80 Minuten telefonieren will
Da Lea in Mathematik gut aufgepasst hat, stellt sie sofort für
beide Tarife die Funktionsgleichungen auf und zeichnet die
Graphen in ein Koordinatensystem. Auf der x - Achse
(unabhängige Variable) trägt sie die Minuten ab und auf der y Achse (abhängige Variable) die Kosten.
Beispiel
a) Tarif B ist der günstigste,
wenn sie50 € im Monat
vertelefonieren will. Dafür
kann sie 200 Minuten
telefonieren.
b) Tarif A ist der günstigste,
wenn sie im Monat nur 80
Minuten telefonieren will.
Dafür zahlt sie 25 €.
Bemerkung:
Bei den meisten Aufgaben aus der Praxis ist vorher genau
zu überlegen, wie das Koordinatensystem anzulegen ist.
Welches ist die unabhängige, welches ist die abhängige
Variable. Welche Werte müssen auf der x - bzw. y - Achse
untergebracht werden. Wie ist der jeweilige Maßstab zu
wählen, um eine anschauliche Graphik zu bekommen. Oft
treten nur positive Werte auf.
Vokabeln
Zusammenfassung der Vokabeln
Lineare Funktion y = f(x) = ax Schnittpunkt mit der y - Achse
+b
Py ( 0 | b )
unabhängige Variable (x Steigungsdreieck
Achse)