Checkliste zum Thema „Lineare Funktionen“

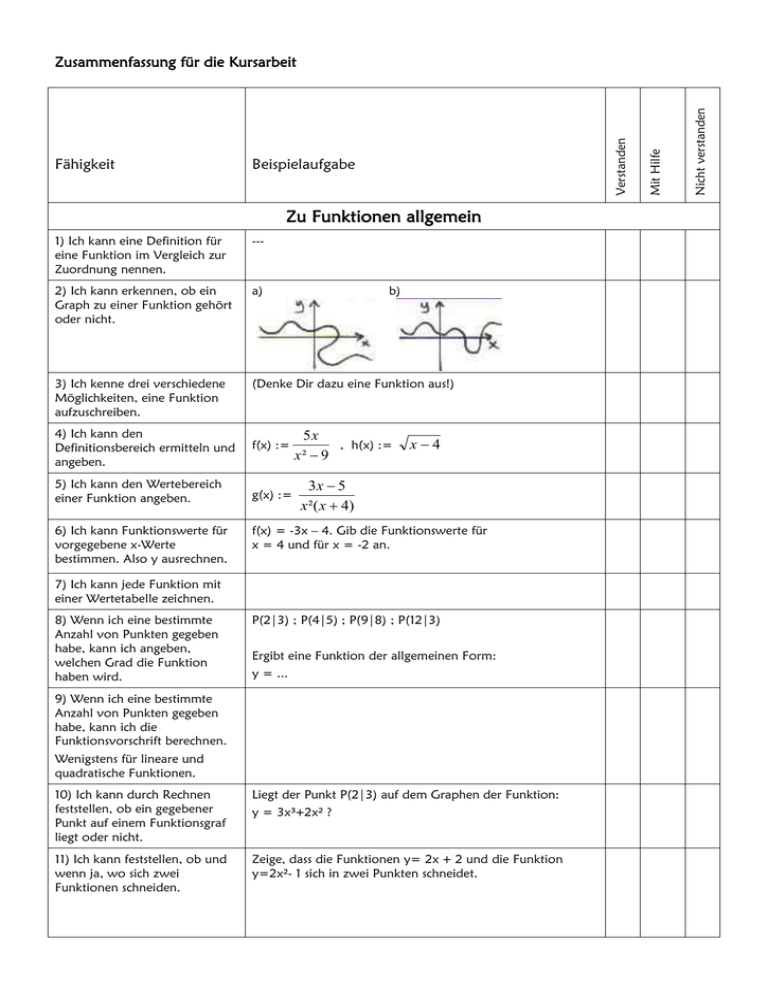
Zu Funktionen allgemein
1) Ich kann eine Definition für
eine Funktion im Vergleich zur
Zuordnung nennen.
---
2) Ich kann erkennen, ob ein
Graph zu einer Funktion gehört
oder nicht.
a)
3) Ich kenne drei verschiedene
Möglichkeiten, eine Funktion
aufzuschreiben.
(Denke Dir dazu eine Funktion aus!)
4) Ich kann den
Definitionsbereich ermitteln und
angeben.
f(x) :=
5) Ich kann den Wertebereich
einer Funktion angeben.
g(x) :=
6) Ich kann Funktionswerte für
vorgegebene x-Werte
bestimmen. Also y ausrechnen.
b)
5x
, h(x) :=
x²  9
x4
3x  5
x ²( x  4)
f(x) = -3x – 4. Gib die Funktionswerte für
x = 4 und für x = -2 an.
7) Ich kann jede Funktion mit
einer Wertetabelle zeichnen.
8) Wenn ich eine bestimmte
Anzahl von Punkten gegeben
habe, kann ich angeben,
welchen Grad die Funktion
haben wird.
P(2|3) ; P(4|5) ; P(9|8) ; P(12|3)
Ergibt eine Funktion der allgemeinen Form:
y = ...
9) Wenn ich eine bestimmte
Anzahl von Punkten gegeben
habe, kann ich die
Funktionsvorschrift berechnen.
Wenigstens für lineare und
quadratische Funktionen.
10) Ich kann durch Rechnen
feststellen, ob ein gegebener
Punkt auf einem Funktionsgraf
liegt oder nicht.
Liegt der Punkt P(2|3) auf dem Graphen der Funktion:
11) Ich kann feststellen, ob und
wenn ja, wo sich zwei
Funktionen schneiden.
Zeige, dass die Funktionen y= 2x + 2 und die Funktion
y=2x²- 1 sich in zwei Punkten schneidet.
y = 3x³+2x² ?
Nicht verstanden
Beispielaufgabe
Mit Hilfe
Fähigkeit
Verstanden
Zusammenfassung für die Kursarbeit
12) Ich kann die Nullstelle einer
Funktion wenigstens für Grad 1
und Grad 2 ermitteln.
13) Ich kann beweisen, ob eine
Funktion punktsymmetrisch
oder achsensymmetrisch ist.
Buch S. 22, S. 23
Beispiel 1+2
14) Ich weiß, was eine
Kurvenschar ist und kann
wenigstens einige
Repräsentanten zeichnen.
Gegeben: ft(x) := tx² +tx – 1
oder
Zeichne: f2(x)
15) Ich kann beweisen, ob eine
Kurvenschar unendlich viele,
eine oder keine Nullstelle oder
hat.
Zeige, dass die Kurvenschar ft(x) := 2tx² genau eine Nullstelle
besitzt.
16) Ich kann zeigen, dass alle
Graphen durch einen festen /
oder keinen festen Punkt gehen!
Beweisen Sie dass alle Graphen der Kurvenschar
Zeichne drei Funktionen der Kurvenschar von ft(x):=4tx² + 2
ft(x) := 2tx +1 durch einen festen Punkt gehen.
Spezielles zu linearen Funktionen
17) Ich kenne die allgemeine
Darstellung einer linearen
Funktion und weiß, was m und
b bedeutet.
18) Ich kann an einer Funktionsgleichung die Steigung und den
Schnittpunkt des Graphen mit
der y-Achse ablesen.
f(x) := -2x + 5
g(x) :=
1
x–3
4
19) Ich kann an einem Graphen
ein Steigungsdreieck einzeichnen
und die Steigung bestimmen.
20) Ich kann den Graphen einer
vorgegebenen Funktion
zeichnen ohne zu rechnen.
21) Ich kann anhand des
Graphen einer Funktion die
zugehörige Funktionsgleichung
aufstellen.
y= 
3
x2
5
Buch S. 19 Nr.
8+9
22) Ich kenne die
Steigungsformel.
m=
23) Ich kann aus 2 Punkten, die
auf dem Funktionsgraphen
liegen, die Steigung des Graphen
bestimmen.
24) Ich kann eine
Funktionsgleichung bestimmen,
wenn ich einen Punkt des
Funktionsgraphen und die
Steigung kenne.
A(-1/2), B(4/-5)
P(2/-3), m =
25) Ich kann anhand eines Texts
einen Funktionsgraphen
zeichnen und diesem
verschiedene Informationen
entnehmen.
1
2
Reisebüro A und Reisebüro B bieten Reisen nach Teneriffa an.
Im Reisebüro A kostet der Flug 250€ und der Aufenthalt im
Hotel pro Tag 50€. Reisebüro B bietet den Flug schon zum
Preis von 150€ an, dafür kostet der Hotelaufenthalt pro Tag
60€.
a) Zeichne für beide Angebote einen Graphen Anzahl der
Urlaubstage  Preis in ein Koordinatensystem.
Lies folgende Informationen am Graphen ab:
b) Wann ist welches Angebot das günstigste? Bei welcher
Reisedauer gibt es keinen Unterschied zwischen beiden
Angeboten?
c) Simon möchte 7 Tage verreisen. Wie viel müsste er in
Reisebüro A und wie viel in Reisebüro B bezahlen?
d) Clara hat 450€ zur Verfügung. Wie lange kann sie dafür
im Reisebüro A und im Reisbüro B verreisen?
26) Ich kenne zwei Darstellungsarten der Betragsfunktion.
Buch S. 16
S. 17 Bsp. 3
27) Ich weiß wie der Graph
einer Betragsfunktion aussieht.
28) Ich kann eine
Betragsfunktion verschieben.
Einfach
nachdenken!
Spezielles zu quadratischen Funktionen
29) Ich kenne zwei
Darstellungsformen der
quadratischen Funktion.
30) Ich kann jeweils eine Form
in die andere Form und
umgekehrt überführen.
(Quadrat Ergänzung und
binomische Formel)
31) Ich weiß, was die
Scheitelpunktform ist, wozu ich
diese brauche und kann diese
auch bestimmen.
32) Ich kann eine quadratische
Funktion zeichnen ohne eine
Wertetabelle aufzustellen.
33) Ich kenne die PQ-Formel
und kann damit z.B. Nullstellen
einer quadratischen Funktion
berechnen.
Spezielles zu Potenzfunktionen
34) Ich kann jede Funktion mit
ganzen Zahlen im Exponenten
skizzieren.
Arbeitsblatt
35) Ich kann die wichtigsten
Eigenschaften benennen.
Arbeitsblatt
Ganzrationale Funktionen
36) Ich kann angeben, ob eine
Funktion ganzrational ist oder
nicht.
37) Ich kann beweisen, ob eine
Funktion punktsymmetrisch
oder achsensymmetrisch ist.
38) Ich kenne die Bedeutung,
ob alle Exponenten gerade oder
ungerade sind.
39) Ich weiß, dass gilt:
y= 2x² -3 hat nur gerade
Hochzahlen hat, da gilt: 3 = 3x0
40) Ich kann einfache
Optimierungsaufgaben, die auf
quadratische Funktionen
hinauslaufen, lösen.
41) Ich kann einfach e
Steckbriefaufgaben lösen.
42) Ich kann Steckbriefaufgaben
mit einem Praxisbezug lösen.
Buch S. 20,
S. 21 Nr 2