Das Leontief-Modell - Warum besucht man www.dreifinger.de?

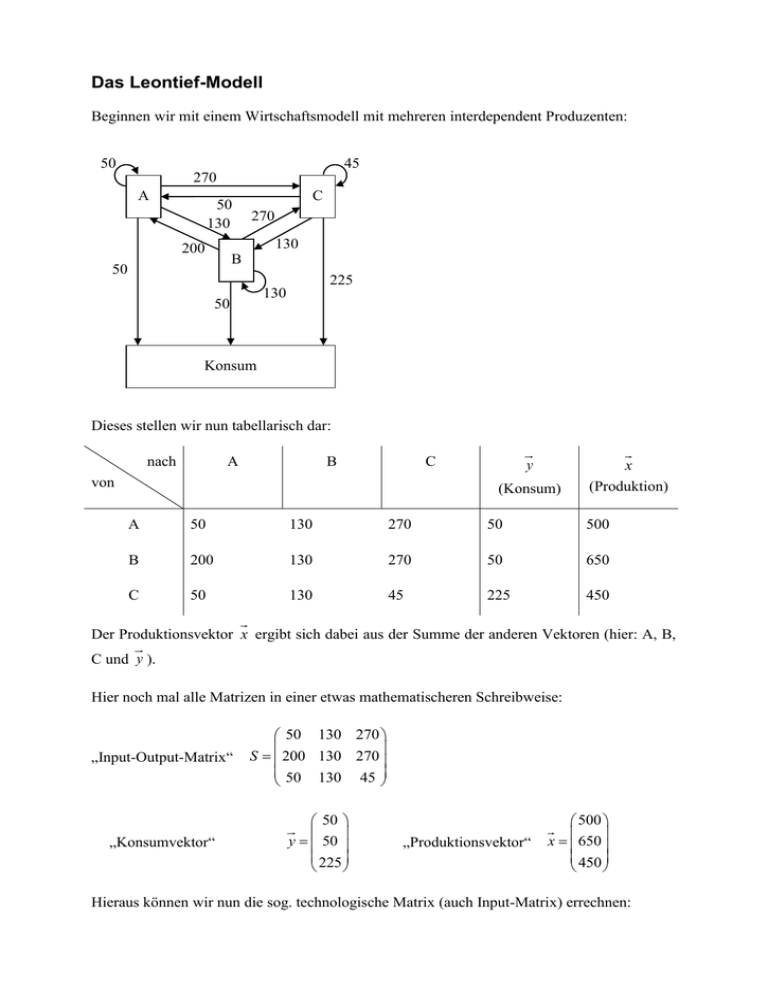
Das Leontief-Modell
Beginnen wir mit einem Wirtschaftsmodell mit mehreren interdependent Produzenten:
50
45
270
A
50
130
C
270
130
200
B
50
225
130
50
Konsum
Dieses stellen wir nun tabellarisch dar:
nach
A
B
C
von
y
(Konsum)
x
(Produktion)
A
50
130
270
50
500
B
200
130
270
50
650
C
50
130
45
225
450
Der Produktionsvektor x ergibt sich dabei aus der Summe der anderen Vektoren (hier: A, B,
C und y ).
Hier noch mal alle Matrizen in einer etwas mathematischeren Schreibweise:
„Input-Output-Matrix“
 50 130 270 


S   200 130 270 
 50 130 45 


„Konsumvektor“
 50 


y   50 
 225 


„Produktionsvektor“
 500 


x   650 
 450 


Hieraus können wir nun die sog. technologische Matrix (auch Input-Matrix) errechnen:
 50
 500

200
A
 500

 50
 500
130
650
130
650
130
650
270 
450   0,1 0, 2 0, 6 

270  

  0, 4 0, 2 0, 6 
450  
0,1 0, 2 0,1 

45  

450 
Das besondere dieser technologischen Matrix ist, dass sie unabhängig von der
Produktionsmenge stets konstant bleibt. Es gelten dabei folgende Zusammenhänge:
y  x  A x
x   E  A  y
1
Dabei bezeichnet man
 E  A
1
als „Leontief-Inverse“. Merke: Nur wenn in der Leontief-
Inverse alle Elemente positiv sind, muss es eine Lösung für x geben.
Rechenbeispiele
 50 
In dem obigen Beispiel konnten y   50  Einheiten verkauft/konsumiert werden. Wie viel
 225 


muss produziert werden, damit von dem ersten Produkt doppelt so viel konsumiert werden
kann, von den beiden anderen allerdings genau so viel?
 100 


Dann muss gelten: y   50  . Laut obiger Formel gilt also für den Produktionsvektor:
 225 


1
  1 0 0   0,1 0, 2 0, 6    100   583,3 


 
 
 
x    0 1 0    0, 4 0, 2 0, 6     50    708,3 
  0 0 1   0,1 0, 2 0,1    225   472, 2 
 
 
 


 550 


Nun kann aber nur x   700  produziert werden. Welcher Konsum ist damit möglich?
 470 


 550   0,1 0, 2 0, 6   550   73 

 
 
 

y   700    0, 4 0, 2 0, 6    700    58 
 470   0,1 0, 2 0,1   470   228 

 
 
 

Ein weiteres Beispiel: eine ganze Volkswirtschaft
Im folgenden Diagramm sind die Produktionsmengen der drei Produktionssektoren sowie
deren Verteilung dargestellt. Die Produktion eines Sektors wird durch die Zahl in dem Kasten
angegeben.
Aufgaben:
132
352
176
I
660
704
292
264
L
880
438
D
1460
a)
y ?
b)
A?
c)
y ?
 500 


x   700 
 350 


292
Konsum
d)
x?
 250 


y   600 
 270 


a)
 660  132  292  176   60 

 

y  1460  292  264  704    200 

880  352  438   90 

 660 


x  1460 
 880 


b)
 132 292
 660 1460

264 292
A
 660 1460

438
 0
 660 1460
176 
880 

704 
880 

352 

880 
c)
d)
190 


y  ( E  A)  x   80 
 0 


 2120 


x  ( E  A)1  y   4520 
 2710 


„Übungen zu 2.5“: Aufgabe 6
Analog zu dem vorherigen Beispiel gilt in einer Volkswirtschaft folgendes Diagramm:
150
Aufgaben:
200
200
A
600
B
800
200
50
100
200
a)
A?
b)
y ?
100
C
400
 x
 
x   x
 x
 
300
100
200
c)
Konsum
x?
 600 


y   300 
 200 


a)


 0, 25 0, 25 0,125 


1
A
0, 25 0, 25 
 3

 1


0
0, 25 
 6

d)
x?
100 


y  100 
100 


b)




 0, 75 0, 25 0,125 
 0,375 x 

  x 

1
   1


y  x  A  x   E  A  x  
0, 75 0, 25   x  
x 
 3
    6

 1
  x  7

 
0
0, 75 
x 

 12 
 6

c)
x   E  A
d)
1
 600  1275 

 

  300   1150 
 200   550 

 

 2175 


100   8 
1275 
1 

x   E  A  100   
 4 
100  



 775 
 4 
„Übungen zu 2.5“: Aufgabe 7
Input
Output
A
B
C
Außenmarkt
A
B
C
952
2720
2720
1904
5440
5440
5712
4080
8160
952
1360
4080
a) Ermitteln Sie die technologische Matrix A.
 952 


y   1360 
 4080 


 9520 


x   9520 
 20400 




 0,1 0, 2 0, 28 


2
4

A
0, 2 
 7

7
 2

4

0, 4 
7
 7

b) Begründen Sie, dass eine Verdoppelung aller Mengen auf dem Absatzmarkt eine
Verdopplung der Gesamtproduktion zur Folge hat.
x   E  A  y
1
x
y
c) Berechnen Sie den Produktionsvektor, wenn alle Mengen auf dem Absatzmarkt um
1470 ME erhöht werden sollen.
Komisch, hier bekomme ich beim Nachrechnen nur noch negativen Müll heraus.
Aufgeschrieben habe ich mir:
x   E  A
1
 2422   709240 

 

  2830   1155440 
 5550  1446450 

 

Diese Produktionsmenge erscheint mir aber etwas zu hoch.
„Übungen zu 2.5“: Aufgabe 8
 0,1 0,1 0, 2 


A   0,3 0, 2 0,1 
 0, 4 0,1 0,3 


 1000 


y   1600 
 4000 


x   E  A
 2000 


x   5000 
 2500 


1
 3435 


 y   4325 
 8195 


 800 


y   E  A  x   3150 
 450 


Aufgaben:
a)
b)
c)
d)