J. Mauch und P. Menzel
Werbung

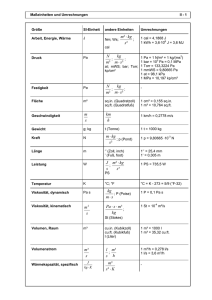
Online-Ergänzung Zum Beitrag Experimentelle Viskositätsvergleiche einfach und anschaulich Struktur-Eigenschaftsbeziehungen entwickeln J. Mauch und P. Menzel Physikalische Grundlagen zur Viskosität In diesem Artikel werden in vereinfachter Form nur die Grundbegriffe aufgeführt, die für das Verständnis der Experimente und der Deutung von Struktur-Eigenschaftsbeziehungen wichtig sind. Die umfangreiche Anleitung der Apparatur enthält sehr ausführliche Zusammenstellungen der theoretischen Grundlagen, Grafiken, Tabellen und eine Fülle von Versuchsanregungen [3]. Recht gute Informationen zum Thema sind auch im Internet (--> Wikipedia--> Viskosität) mit zahlreichen Grafiken, Tabellen und Literaturhinweisen zu finden. Strömende Flüssigkeiten oder Gase setzen der Fließbewegung einen Widerstand entgegen, sie besitzen eine bestimmte Viskosität. Diese Viskosität - auch als Zähigkeit oder innere Reibung bezeichnet - beruht auf der Gesamtheit der Kräfte, die zwischen zwei mit verschiedener Geschwindigkeit strömenden Schichten eines Stoffs wirksam sind. Die Viskosität ist die Fähigkeit eines Stoffs, der gegenseitigen laminaren Verschiebung zweier benachbarter Schichten einen Reibungswiderstand entgegenzusetzen. Sie ist also ein Maß für die Geschwindigkeit, mit der sich ein Körper unter dem Einfluss einer bestimmten Kraft verformt. Bereits 1687 stellte Newton für die Abhängigkeit des Geschwindigkeitsgefälles von dieser Kraft folgende Beziehung auf: 𝒅𝒗 𝑭 = 𝜼 𝑨 𝒅𝒙 𝜼= 𝑭 𝒅𝒙 𝑨 𝒅𝒗 F Kraft A Fläche dv Geschwindigkeitsunterschied dx Abstand η dynamische Viskosität Der Faktor η , die sogenannte Dynamische Viskosität, ist also das Verhältnis der Schubspannung τ ( F/A) zum Geschwindigkeitsgradienten D (dv/dx) senkrecht zur Strömungsrichtung: 𝞽 𝜼=𝑫 SI-Einheit Pascalsekunde (Pa●s) Alte Einheit Poise (P): 1 P = 0,1 Pa●s Diese dynamische Viskosität ist für viele Flüssigkeiten und Gase eine Stoffkonstante wie z.B. die Dichte, die Oberflächenspannung oder die Siedetemperatur. Sie muss nach dem oben Angeführten ein Maß für die Wechselwirkung zwischen den Schichten sein und damit auch Rückschlüsse auf die Struktur der betreffenden Stoffe ermöglichen. Langsam fließende, zähe Stoffe haben hohe Werte für η, dünnflüssige, schnellfließende entsprechend niedrigere Werte. Der Einfachheit halber wird in der Folge der Begriff " Viskosität“ für die dynamische Viskosität η verwendet, was der Bedeutung und dem normalen Sprachgebrauch entspricht. Viskosität von Gasen Experimentelle Untersuchungen zeigen, dass die Viskosität von Gasen um 1 bis 2 Zehnerpotenzen kleiner ist als bei Flüssigkeiten und auch anderen Gesetzen gehorcht. Dies ist verständlich, wenn man sich vor Augen hält, dass der mittlere Molekülabstand in Gasen sehr groß ist gegenüber dem Moleküldurchmesser, während in Flüssigkeiten der mittlere Molekülabstand in der Größenordnung des Moleküldurchmessers liegt. Die Viskosität von Gasen kann demnach nicht wie bei den Flüssigkeiten eine Folge der Anziehungskräfte zwischen den Teilchen sein, die nur auf geringe Abstände wirksam werden, sondern wird durch Zusammenstöße der Moleküle verursacht. Durch die Zusammenstöße wird die Strömungsbewegung in einem Gas von einer Schicht zur anderen übertragen. Bewegt sich ein Teilchen aus einer langsamen in eine schnellere Schicht, so wirkt es dort bremsend. Die umgekehrte Bewegung führt zu einer Beschleunigung der langsameren Schicht. Wie die kinetische Gastheorie zeigt, hängt die dynamische Viskosität eines idealen Gases überraschenderweise weder vom Druck noch von der Dichte ab, sie steigt aber mit Zunahme der Temperatur, weil damit auch die kinetische Energie zunimmt. Viskosität von Flüssigkeiten Bei Flüssigkeiten ist der Teilchenabstand so gering, dass hier die intermolekularen Anziehungskräfte die eigentliche Ursache der Viskosität sind. Dies wird besonders deutlich, wenn man annimmt, dass Flüssigkeiten eine mehr oder weniger aufgelockerte Gitterstruktur haben, die durch unbesetzte Plätze, sogenannte "Löcher", stellenweise gestört ist. Diese Löcher sind für die Beschreibung von Fließ- und Diffusionsvorgängen in Flüssigkeiten von entscheidender Bedeutung. Nach Eyring [5] erfolgt die Molekülbewegung über die Löcher bevorzugt unter dem Einfluss des Geschwindigkeits- bzw. Konzentrationsgefälles. Die Moleküle bewegen sich dabei über einen Potentialberg auf neue Gitterplätze. Abb. 4: Modellvorstellung des Fließvorganges in Flüssigkeiten nach Eyring [4] Die dazu erforderliche Aktivierungsenergie hängt von der Art der Wechselwirkung ab, die Viskosität muss also Rückschlüsse auf diese Kräfte erlauben. Auch andere physikalische Eigenschaften von Flüssigkeiten wie Dichte und Siedetemperatur hängen ebenfalls von diesen Kräften ab. Damit lassen sich Regeln für Zusammenhänge entwickeln. In der folgenden Tabelle 2 sind für einige Flüssigkeiten diese Werte tabelliert. Die Flüssigkeiten sind dabei nach steigender Viskosität angeordnet. Zwischen Viskosität und Siedetemperatur bzw. Dichte lässt sich zunächst nicht der erwartete Zusammenhang erkennen. Dieser erschließt sich erst, wenn die Flüssigkeiten bestimmten Stoffklassen zugeordnet werden. Tab. 1: Dichte und Siedetemperatur einiger Flüssigkeiten geordnet nach steigender Viskosität bei 20 0C [5] Stoff Diethylether Ethanol Chlorethan Hexan Aceton Essigsäuremethylester Schwefelkohlenstoff Bromethan Heptan Dichlormethan Essigsäureethylester Octan Chloroform Essigsäurepropylester Iodethan Methanol Benzol Nonan Chlorbenzol Decan Tetrachlormethan Brom Wasser Brombenzol Ethanol Propanal Iodbenzol Quecksilber Propanol -1 Propanol -2 Glycol Schwefelsäure Glycerin η (mPa · s) 0,243 0,2615 0,266 0,320 0,3225 0,381 0,367 0,392 0,4105 0,4355 0,449 0,538 0,546 0,584 0,585 0,591 0,649 0,711 0,80 0,92 0,969 0,995 1,002 1,13 1,200 1,41 1,49 1,554 2,256 2,39 19,9 25,4 1495,0 Dichte (g ·cm -2) 0,736/ 0º 0,788/ 13º 0,917/ 6º 0,600 0,795 0,974 1,263 1,459 0,684 1,336 0,900 0,702 1,498/ 15º 0,891/ 18º 1,933 0,792 0,879 0,718 1,106 0,730 1,596 3,14 0,998 1,484 0,789 1,046/ 24º 1,823/ 25º 13,545 0,804 0,785 1,113 1,834 1,261 Sdt (º C) 34,6 20,2 13,1 68,6 56,1 31,8 46,5 38,4 98,4 40,7 77,1 125,8 61,2 101,6 72,3 64,7 80,1 150,6 131,7 173,8 76,7 58,7 100,0 155,6 78,4 72,0 188,6 356,9 97,2 82,0 197,4 338 z. 173/ 11 Torr