1. Aufgabe: Materialverflechtung (20P)
Werbung
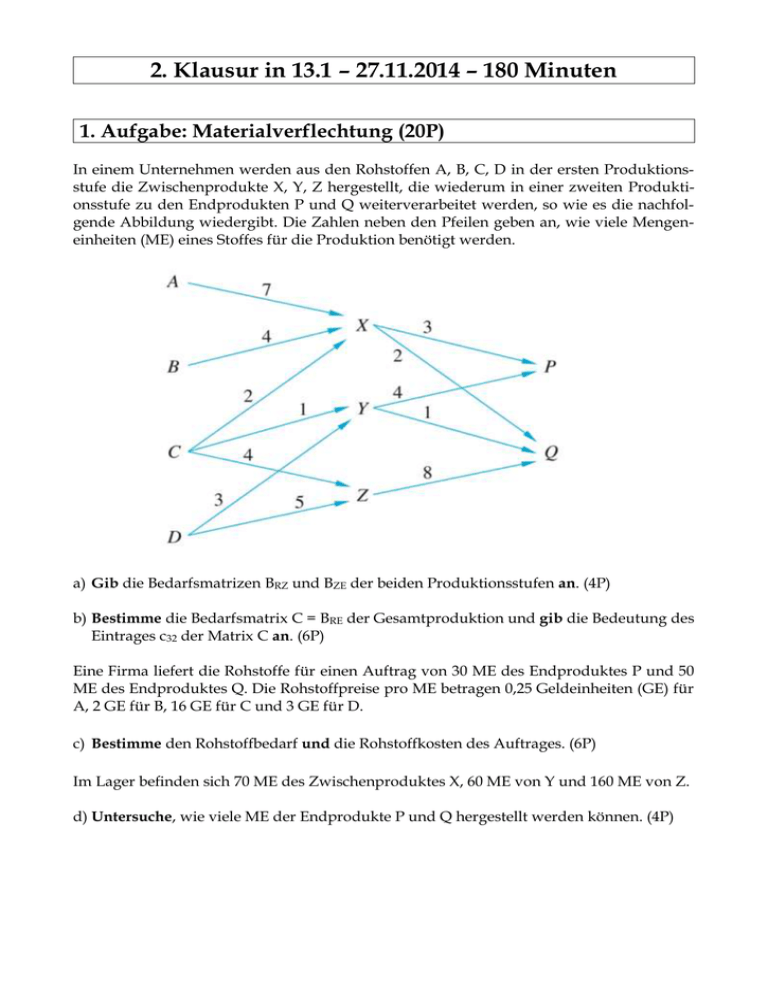
2. Klausur in 13.1 – 27.11.2014 – 180 Minuten 1. Aufgabe: Materialverflechtung (20P) In einem Unternehmen werden aus den Rohstoffen A, B, C, D in der ersten Produktionsstufe die Zwischenprodukte X, Y, Z hergestellt, die wiederum in einer zweiten Produktionsstufe zu den Endprodukten P und Q weiterverarbeitet werden, so wie es die nachfolgende Abbildung wiedergibt. Die Zahlen neben den Pfeilen geben an, wie viele Mengeneinheiten (ME) eines Stoffes für die Produktion benötigt werden. a) Gib die Bedarfsmatrizen BRZ und BZE der beiden Produktionsstufen an. (4P) b) Bestimme die Bedarfsmatrix C = BRE der Gesamtproduktion und gib die Bedeutung des Eintrages c32 der Matrix C an. (6P) Eine Firma liefert die Rohstoffe für einen Auftrag von 30 ME des Endproduktes P und 50 ME des Endproduktes Q. Die Rohstoffpreise pro ME betragen 0,25 Geldeinheiten (GE) für A, 2 GE für B, 16 GE für C und 3 GE für D. c) Bestimme den Rohstoffbedarf und die Rohstoffkosten des Auftrages. (6P) Im Lager befinden sich 70 ME des Zwischenproduktes X, 60 ME von Y und 160 ME von Z. d) Untersuche, wie viele ME der Endprodukte P und Q hergestellt werden können. (4P) 2. Aufgabe: Population von Vögeln (20P) Die jährliche Entwicklung der Population einer Vogelart bestehend aus Jung- (1) und Altvögeln (2) ist durch den folgenden Übergangsgraphen gegeben: a) Gib zu dem Übergangsgraphen eine Übergangsmatrix U an. (4P) b) Beschreibe anhand des Übergangsgraphen, nach welchen Modellannahmen die Entwicklung der Population dieser Vogelart abläuft. (3P) Die Population besteht zu Beobachtungsbeginn aus 80 Jungvögeln und 110 Altvögeln. c) Berechne den Bestandsvektor nach einem Jahr sowie den Bestandsvektor des Vorjahres. (6P) d) Bestimme, wie viel Prozent der Jungvögel drei Jahre alt werden. (3P) Um die Population konstant zu halten, soll der Ausgangsbestand an Altvögeln durch Tötung so verändert werden, dass er sich innerhalb eines Jahres nicht mehr ändert. Die Anzahl an Jungvögeln bleibt unverändert. e) Untersuche, wie viele Altvögel getötet werden müssen, damit der Bestandsvektor von Jahr zu Jahr unverändert bleibt. (4P) 3. Aufgabe: Entwicklung von Wirtschaftssektoren (40P) Der französische Nationalökonom Jean Fourastié stellte 1949 eine Theorie zur wirtschaftlichen Entwicklung von Entwicklungsländern auf. Danach sind in der vorindustriellen Gesellschaft die meisten Erwerbstätigen im primären Wirtschaftssektor I (Forst- und Landwirtschaft), in Folge der industriellen Revolution immer mehr Erwerbstätige im sekundären Sektor II (Industrie und produzierendes Gewerbe) und schließlich in der postindustriellen Gesellschaft die meisten Erwerbstätigen im tertiären Sektor III (Dienstleistungen) beschäftigt. Nach Fourastié bewirkt das wirtschaftliche Wachstum eine Verlagerung des Schwerpunktes der Wirtschaft vom primären über den sekundären zum tertiären Sektor. Zwei Modelle F1 und F2 sollen nun den Entwicklungsprozess der Beschäftigungsanteile zwischen den drei Wirtschaftssektoren über einen Zeitraum von 10 Jahre beschreiben. Die folgenden Tabellen 1 und 2 beschreiben diesen Prozess: von I II III I 0,75 0,10 0,15 F2 II 0 0,90 0,10 III 0 0 1 Tabelle 1: Modell F1 nach nach F1 von I II III I 0,50 0,20 0,30 II 0,01 0,60 0,39 III 0,01 0,12 0,87 Tabelle 2: Modell F2 Die folgende Tabelle 3 gibt die prozentualen Verteilungen der Beschäftigten auf die drei Wirtschaftssektoren in den USA für die Jahre 1980, 1990 und 2000 an: Sektor I Landwirtschaft II Industrie III Dienstleistung Jahr 1980 0,04 0,30 0,66 1990 0,03 0,27 0,70 2000 0,02 0,24 0,74 Tabelle 3: Prozentuale Verteilung der Beschäftigten auf die drei Sektoren a) Gib die Übergangsmatrizen F1 und F2 für die beiden Modelle an, und zeige, dass es sich in beiden Fällen um einen Austauschprozess handelt. (3P) b) Berechne F12 und F22 und gib ihre Bedeutungen im Sachzusammenhang an. (5P) Es sei ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v1980 die prozentuale Verteilung der Erwerbstätigen auf die drei Wirtschaftssektoren im Jahr 1980 (vgl. Tabelle 3). c) Ermittle für beide Modelle jeweils ⃗⃗⃗⃗⃗⃗⃗⃗⃗ v1990 und ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2000 und entscheide, ob F1 und/oder F2 gute Modelle für die wirtschaftliche Entwicklung in den USA im Zeitraum von 1980 bis 2000 sind. (10P) 0 0 Es gilt F1 80 = (0 0 1 1 0,02 0,02 0,02 0 0) und F2 20 = (0,23 0,23 0,23). 0,75 0,75 0,75 1 d) Interpretiere die Matrizen F1 80 und F2 20 im obigen Sachzusammenhang und entscheide mit Hilfe dieser beiden Matrizen, welches der beiden Modelle langfristig realistischer ist. (5P) e) Ermittle für das Modell F2 mithilfe des Ansatzes F2 v ⃗ =v ⃗ eine stationäre Verteilung v ⃗ und erkläre die Bedeutung der stationären Verteilung im Sachzusammenhang. (6P) Die Rohstoffreserven werden immer knapper. Ökologische Probleme zwingen die Politik zum Handeln. Der ökologische Landbau soll gestärkt werden. Der prozentuale Anteil der Beschäftigten im Industriesektor II sinkt immer weiter. Wegen politischer Vorgaben lautet die Übergangsmatrix F3 zwischen den drei Wirtschaftssektoren ab dem Jahr 2000 (F3 beschreibt wie F1 und F2 den Austauschprozess über einen Zeitraum von zehn Jahren): 1 0,10 0 F3 = (0 0,50 0). 0 0,40 1 f) Bestimme die Verteilung der Beschäftigten auf die einzelnen Sektoren unter diesen Voraussetzungen im Jahr 2020. (4P) [Hinweis: Verwende für die Startverteilung die Werte des Jahres 2000 aus Tabelle 3.] Es gilt: lim F3 n→∞ n 1 0,20 0 = (0 0 0,80 0 0) 1 g) Beschreibe, wie sich unter diesen Voraussetzungen die relative Verteilung der einzelnen Wirtschaftssektoren langfristig entwickelt. (2P) Zahlreiche Lobbyisten des Industriesektors üben Druck auf die Politik aus. Sie wollen ein Aussterben des Industriesektors verhindern. Es wird vertraglich vereinbart, dass ab dem Jahr 2040 durch gezielte Fördermaßnahmen des Industriesektors für zehn Jahre eine Verteilung hin zum Industriesektor stattfindet. Anschließend verlaufen die Vorgaben wieder nach dem Modell F3. Folgende Korrekturmatrix K wird vereinbart: 0,60 0 0 K = (0,40 1 0,40) 0 0 0,60 h) Ermittle unter Berücksichtigung der Matrizen F3 und K sowie der prozentualen Verteilung ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2000 einen Term für den Vektor ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2050 , der die prozentuale Verteilung der Beschäftigten im Jahr 2050 beschreibt. (2P) [Hinweis: Hier muss nicht gerechnet werden.] i) Beurteile, ob das Ergebnis für ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2050 beeinflusst würde, wenn die gleiche Korrektur 20 Jahre früher erfolgte. (3P) 4. Aufgabe: Wirkstoffkonzentration einer Droge (20P) Wenn jemand Drogen oder Aufputschmittel nimmt, vergeht eine gewisse Zeit, bis diese „so richtig anschlagen“. Die folgende Funktion k beschreibt für t 0 näherungsweise die Drogenkonzentration in Abhängigkeit von der Zeit t: 𝐤(𝐭) = 𝟏, 𝟓 ∙ (𝐞−𝟎,𝟐𝐭 − 𝐞−𝟒𝐭 ) = 𝟏, 𝟓 ∙ 𝐞−𝟎,𝟐𝐭 ∙ (𝟏 − 𝐞−𝟑,𝟖𝐭 ) Als Bezugsgröße für die Konzentration des Mittels im Körper wird das Blutplasma verwendet. Als Einheit für k(t) wählt man mg Wirkstoff pro Liter Blutplasma. Die Zeit t wird in Stunden angegeben. Zum Zeitpunkt t = 0 wird die Droge eingenommen. Der Graph ist im Folgenden angegeben. a) Begründe, dass es bei der Darstellung der Wirkstoffkonzentration durch die Funktion k nie zu einem vollständigen Abbau der Droge im Blut des Konsumenten kommt. (2P) b) Untersuche, nach welcher Zeit die Konzentration der Droge im Blutplasma am größten ist, und gib die maximale Konzentration an. (6P) [Zur Kontrolle: k´(t) = 1,5 ∙ e−0,2t ∙ (4e−3,8t − 0,2); Hinweis: Ränder nicht vergessen!] c) Zeige, dass die momentane Änderungsrate der Wirkstoffkonzentration der Droge für den Zeitabschnitt 0 ≤ t < t W = stetig anwächst. (4P) ln(400) 3,8 kontinuierlich abnimmt und für t > t W = ln(400) 3,8 [Zur Kontrolle: k´´(t) = 1,5 ∙ e−0,2t ∙ (0,04 − 16e−3,8t ); Hinweis: Ohne Nachweis darf verwendet werden, dass k´´´(t) = 1,5 ∙ e−0,2t ∙ (64e−3,8t − 0,008).] Der Inhalt der Fläche zwischen dem Graphen von k und der t-Achse ist ein Maß für die sogenannte Bioverfügbarkeit der verabreichten Droge. d) Zeige durch Integration, dass K mit K(t) = 1,5 ∙ e−0,2t ∙ (0,25 ∙ e−3,8t − 5) eine Stammfunktion zu k ist. (3P) e) Berechne die Maßzahl A der Fläche zwischen dem Graphen von k und der t-Achse im Intervall [0; 10] sowie die Maßzahl der Fläche zwischen dem Graphen von k und der tAchse im Intervall [0; t] für t → +. (5P) Lösungen 1. Aufgabe (20P) 7 = (4 2 0 0 0 1 3 0 3 2 0) und B = ( a) BRZ 4 1) (4P) ZE 4 0 8 5 7 0 0 21 14 3 2 4 0 0 b) Ansatz: C = BRZ ∙ BZE = ( ) ∙ (4 1) = ( 12 8 ) (4P), Bedeutung von 37: Für 1 ME Q benötigt 2 1 4 10 𝟑𝟕 0 8 0 3 5 12 43 man 37 ME C. (2P) 1330 21 14 30 12 8 c) Ansatz: x⃗ = C ∙ y ⃗ ⇔ x⃗ = ( ) ∙ ( ) = ( 760 ) (4P) 10 37 2150 50 12 43 2510 1330 T T ⃗⃗⃗⃗ ⃗⃗⃗⃗ Ansatz: K = k ∙ C ∙ y ⃗ = k ∙ x⃗ ⇔ (0,25 2 16 3) ∙ ( 760 ) = 43782,50 GE (2P) 2150 2510 3 2 𝟕𝟎 p d) Ansatz: (4 1) ∙ (q) = ( 60 ) ⇔ 3p + 2q = 𝟕𝟎, 4p + q = 60, 8q = 160 ⇔ p = 10, q = 20. (4P) 0 8 160 2. Aufgabe (20P) 0 a) U = ( 0,5 0,8 ) (4P) 0,6 b) (3P) Die jährliche Überlebensrate der Jungvögel beträgt 50 %. Die jährliche Geburtenrate beträgt 80 %, d. h. Jeder Altvogel bekommt 0,8 Junge. Die jährliche Überlebensrate der Altvögel beträgt 60 %. c) (6P) 0 ( 0,5 0 ( 0,5 0,8 80 88 )∙( )=( ) (3P) 0,6 110 106 𝑥 𝑥 0,8 80 100 ) ∙ (𝑦 ) = ( ) ⇒ (𝑦 ) = ( ) (3P) 0,6 110 100 d) p = 0,5 ∙ 0,6 ∙ 0,6 = 0,18 = 18 % (3P) e) ( 0 0,5 80 80 0,8 ) ∙ ( ) = ( ) ⇒ 0,8𝑦 = 80 ⇒ 𝑦 = 100; Es müssen zehn Altvögel getötet werden. (4P) 𝑦 𝑦 0,6 3. Aufgabe (40P) 0,75 0 0 0,50 0,01 0,01 a) F1 = (0,10 0,90 0) und F2 = (0,20 0,60 0,12). Es handelt sich in beiden Fällen um Austauschpro0,15 0,10 1 0,30 0,39 0,87 zesse, da beide Matrizen quadratisch sind, nicht negative Einträge und Spaltensumme 1 haben. (3P) 0,5625 0 0 0,255 0,0149 0,0149 b) F1 2 = ( 0,165 0,81 0) und F2 2 = (0,256 0,4088 0,1784). Diese beiden Matrizen beschreiben je0,2725 0,19 1 0,489 0,5763 0,8067 weils den Austauschprozess zwischen den Wirtschaftssektoren über einen Zeitraum von 20 Jahren. (5P) c) 0,04 0,03 0,03 0,75 0 0 0,0225 Modell F1: ⃗⃗⃗⃗⃗⃗⃗⃗⃗ v1990 = (0,10 0,90 0) ∙ (0,30) = (0,274); ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2000 = F1 ∙ (0,274) = (0,2496) (4P) 0,66 0,696 0,696 0,15 0,10 1 0,7279 0,04 0,0296 0,0296 0,50 0,01 0,01 0,024504 Modell F2: ⃗⃗⃗⃗⃗⃗⃗⃗⃗ v1990 = (0,20 0,60 0,12) ∙ (0,30) = (0,2672); ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2000 = F2 ∙ (0,2672) = (0,250624) (4P) 0,66 0,7032 0,7032 0,30 0,39 0,87 0,724872 Für die ersten zehn Jahre scheinen beide Modelle die Realität gut abzubilden, für die zweite Dekade weicht Modell 2 gerade für den Sektor I stärker vom tatsächlichen wert ab als Modell 1. (2P) d) F1 80 beschreibt den Austauschprozess der Sektoren unter Modell 1 über einen Zeitraum von 800 Jahren. Langfristig sterben nach diesem Modell also die ersten beiden Sektoren aus. F2 20 beschreibt die Entwicklung über einen Zeitraum von 200 Jahren nach dem zweiten Modell. Hier werden langfristig 75 % Beschäftigte im Sektor III, 23 % in Sektor II und 2 % in Sektor I arbeiten. Realistischer schein das zweite Modell zu sein, da alle Sektoren weiter bestehen bleiben. (5P) x x x 0,50 0,01 0,01 −0,50 0,01 0,01 0 e) (0,20 0,60 0,12) ∙ (y) = (y) ⇔ ( 0,20 −0,40 0,12 ) ∙ (y) = (0). Mit der zusätzlichen Bedinz z z 0,30 0,39 0,87 0,30 0,39 −0,13 0 gung x + y + z = 1 erhält man mit dem TR (wähle zwei Gleichung des homogenen LGS sowie die Zu1 155 165 satzbedingung) die Lösungen x = ≈ 0,02, y = ≈ 0,23 und z = ≈ 0,75. Die stationäre Verteilung 51 663 221 beschreibt eine Verteilung, die sich langfristig einstellt und sich unter dem Austauschprozess nicht mehr ändert. (6P) f) v2020 = F3 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 2 1 ∙v ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 2020 = (0 0 0 2 0,02 1 0) ∙ (0,24) = (0 1 0,74 0 0,10 0,50 0,40 0,15 0,25 0,60 0,02 0 0,056 0) ∙ (0,24) = ( 0,06 ) (4P) 0,74 1 0,884 x + 0,20y x 1 0,20 0 0 0 0) ∙ (y) = ( g) (0 ). Langfristig würde unter dem dritten Modell der Industriesektor ausz 0,80y + z 0 0,80 1 sterben. (2P) 4 h) ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2050 = K ∙ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2040 = K ∙ F3 ∙ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2000 (2P) i) Das Ergebnis würde beeinflusst werden, da K und F3 2 nicht kommutativ (vertauschbar sind). Denn für Gleichheit müsste gelten: K ∙ F3 4 ∙ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2000 = K ∙ F3 2 ∙ F3 2 ∙ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2000 = F3 2 ∙ K ∙ F3 2 ∙ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ v2000 . 0,60 0 0 0,60 0,09 0 1 0,15 0 K ∙ F3 2 = (0,40 1 0,40) ∙ (0 0,25 0) = (0,40 0,55 0,40) 0 0 0,60 0 0,36 0,60 0 0,60 1 0,60 0 0 1 0,15 0 0,66 0,15 0,06 ≠ F3 2 ∙ K = (0 0,25 0) ∙ (0,40 1 0,40) = (0,10 0,25 0,10) (3P) 0 0 0,60 0 0,60 1 0,24 0,60 0,84 4. Aufgabe (20P) a) k(t) = 1,5 ∙ (e−0,2t − e−4t ) = 1,5 ∙ e−0,2t ∙ (1 − e−3,8t ) > 0, da 0 < e−3,8t < 1 für t > 0. (2P) b) k´(t) = 1,5 ∙ e−0,2t ∙ (4e−3,8t − 0,2) = 0 ⇔ 4e−3,8t = 0,2 ⇔ e−3,8t = 0,05 ⇔ t = k´´(t) = 1,5 ∙ e−0,2t ∙ (0,04 − 16e−3,8t ); k´´ ( ln(20) 3,8 ) = 1,5 ∙ e ln(20) −0,2∙ 3,8 ln(0,05) ∙ (0,04 − 16e −3,8 = ln(20) −3,8∙ 3,8 ln(20) 3,8 ≈ 0,79 (2P) ) ≈ −0,97 < 0. (2P) (denkbar wäre auch der Nachweis eines VZW von k´ an der Extremstelle mit k´(0) > 0 und k´(1) < 0) t= k( ln(20) 3,8 ≈ 0,79 ist lokale Maximumstelle mit der dazugehörigen maximalen Wirkstoffkonzentration ln(20) 3,8 ) = 1,5 ∙ e ln(20) 3,8 −0,2∙ ∙ (1 − e ln(20) 3,8 −3,8∙ ) ≈ 1,22. Wegen k(0) = 0 und lim k(t) = 0. ist das innere Maxit→∞ mum global. (2P) c) Zu zeigen ist, dass die Funktion k bei t W = k´´ ( ln(400) ln(400) 3,8 3,8 ) = 0 und k´´´ ( d) K(t) = 1,5 ∙ ( 1 −0,2 e−0,2t − 1 −4 ) = 1,5 ∙ e ln(400) −0,2∙ 3,8 ln(400) 3,8 ∙ (64e eine Rechts-Links-Wendestelle hat. Wegen ln(400) −3,8∙ 3,8 − 0,008) ≈0,17 > 0 (RELIPO) (4P) e−4t ) = 1,5 ∙ (−5e−0,2t + 0,25e−4t ) = 1,5 ∙ e−0,2t ∙ (0,25 ∙ e−3,8t − 5) (3P) 10 e) ∫0 k(t)dt = K(10) − K(0) = 1,5 ∙ e−2 ∙ (0,25 ∙ e−38 − 5) − 1,5 ∙ (0,25 − 5) ≈ −1,02 + 7,125 ≈ 6,11 (2P) ∞ R ∫0 k(t)dt = lim ∫0 k(t)dt = K(R) − K(0) = lim (1,5 ∙ e−0,2R ∙ (0,25 ∙ e−3,8R − 5) + 7,125) = 7,125 (3P) 𝑅→∞ 𝑅→∞ Mögliche Punktzahl Name: 1 2 3 4 a) b) c) d) a) b) c) d) e) a) b) c) d) e) f) g) h) i) Du gibst die Bedarfsmatrizen an. Du bestimmst die Bedarfsmatrix des Gesamtprozesses … gibst … an. Du bestimmst Rohstoffbedarf und Rohstoffkosten des Auftrages. Du untersuchst, wie viel ME der Endprodukte P und Q … Du gibst die Populationsmatrix an. Du beschreibst, nach welchen Modellannahmen … Du berechnest … Du bestimmst, wie viel Prozent der Jungvögel drei Jahre alt werden. Du untersuchst … Du gibst an, … Du berechnest … und gibst an … Du ermittelst … und entscheidest … Du interpretierst … und entscheidest … Du ermittelst eine stationäre Verteilung und gibst … an. Du bestimmst die Verteilung … Du beschreibst … Du ermittelst … Du beurteilst … a) b) c) d) e) Du begründest … Du untersuchst … Du zeigst … Du zeigst … Du berechnest … I I II III I II II II III I I II II II II II III III II II II-III II II-III Summe (Aufgabe 1) 4 6 6 4 20 Summe (Aufgabe 2) 4 3 6 3 4 20 Summe (Aufgabe 3) 3 5 10 5 6 4 2 2 3 40 Summe (Aufgabe 4) 2 6 4 3 5 20 Punktzahl Aufgabe 1 Punktzahl Aufgabe 2 Punktzahl Aufgabe 3 Punktzahl Aufgabe 4 Gesamtpunktzahl 20 20 40 20 100 Note Punktabzug wegen mangelnder Darstellungsleistung (bis zu 3 Punkten möglich) Datum und Unterschrift Solingen, den 27.11.2014 Endnote Erreichte Punktzahl