Zu bearbeiten sind die Aufgaben 2 und 3a – d

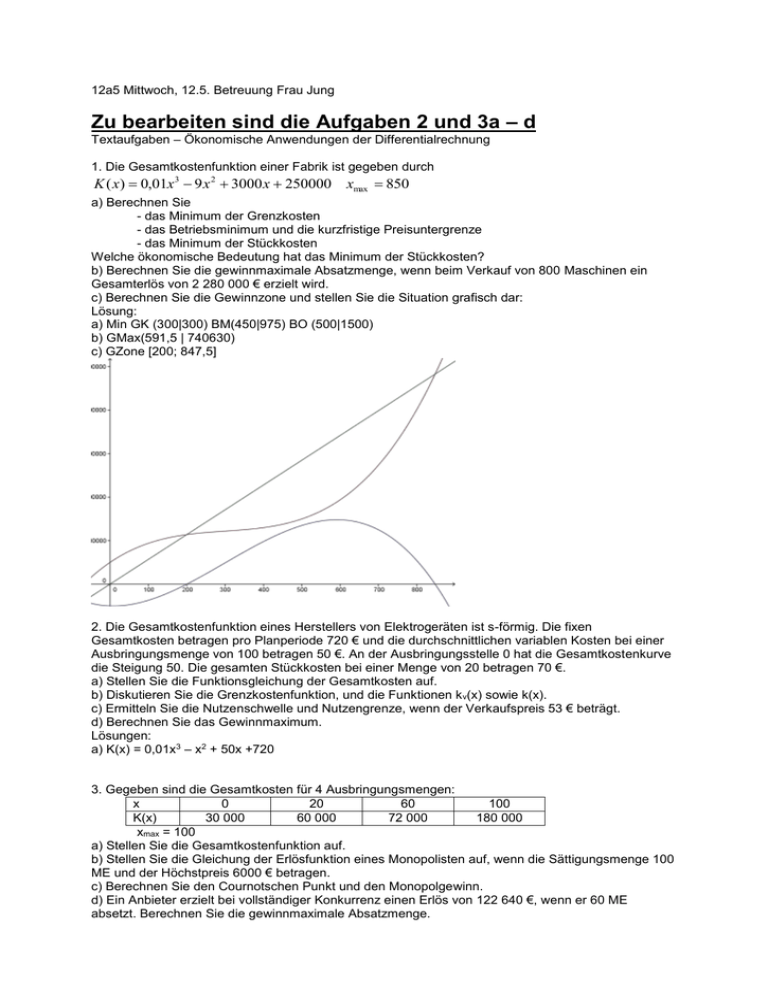
12a5 Mittwoch, 12.5. Betreuung Frau Jung
Zu bearbeiten sind die Aufgaben 2 und 3a – d
Textaufgaben – Ökonomische Anwendungen der Differentialrechnung
1. Die Gesamtkostenfunktion einer Fabrik ist gegeben durch
K ( x)  0,01x 3  9 x 2  3000 x  250000
xmax  850
a) Berechnen Sie
- das Minimum der Grenzkosten
- das Betriebsminimum und die kurzfristige Preisuntergrenze
- das Minimum der Stückkosten
Welche ökonomische Bedeutung hat das Minimum der Stückkosten?
b) Berechnen Sie die gewinnmaximale Absatzmenge, wenn beim Verkauf von 800 Maschinen ein
Gesamterlös von 2 280 000 € erzielt wird.
c) Berechnen Sie die Gewinnzone und stellen Sie die Situation grafisch dar:
Lösung:
a) Min GK (300|300) BM(450|975) BO (500|1500)
b) GMax(591,5 | 740630)
c) GZone [200; 847,5]
2. Die Gesamtkostenfunktion eines Herstellers von Elektrogeräten ist s-förmig. Die fixen
Gesamtkosten betragen pro Planperiode 720 € und die durchschnittlichen variablen Kosten bei einer
Ausbringungsmenge von 100 betragen 50 €. An der Ausbringungsstelle 0 hat die Gesamtkostenkurve
die Steigung 50. Die gesamten Stückkosten bei einer Menge von 20 betragen 70 €.
a) Stellen Sie die Funktionsgleichung der Gesamtkosten auf.
b) Diskutieren Sie die Grenzkostenfunktion, und die Funktionen k v(x) sowie k(x).
c) Ermitteln Sie die Nutzenschwelle und Nutzengrenze, wenn der Verkaufspreis 53 € beträgt.
d) Berechnen Sie das Gewinnmaximum.
Lösungen:
a) K(x) = 0,01x3 – x2 + 50x +720
3. Gegeben sind die Gesamtkosten für 4 Ausbringungsmengen:
x
0
20
60
100
K(x)
30 000
60 000
72 000
180 000
xmax = 100
a) Stellen Sie die Gesamtkostenfunktion auf.
b) Stellen Sie die Gleichung der Erlösfunktion eines Monopolisten auf, wenn die Sättigungsmenge 100
ME und der Höchstpreis 6000 € betragen.
c) Berechnen Sie den Cournotschen Punkt und den Monopolgewinn.
d) Ein Anbieter erzielt bei vollständiger Konkurrenz einen Erlös von 122 640 €, wenn er 60 ME
absetzt. Berechnen Sie die gewinnmaximale Absatzmenge.
e) Wie wirkt sich eine Preiserhöhung um h € (im Fall d) auf die gewinnmaximale Absatzmenge und
den Maximalgewinn aus?
f) Berechnen Sie die Änderungen zu e für h = 456.
g) Wie wirkt sich eine Änderung der Fixkosten auf die gewinnmaximale Menge und den Gewinn aus?
Lösungen:
a) K(x)=0,5x^3 – 60x^2 + 2500x + 30000
b) p(x)= -60x +6000 und E(x) = - 60x^2 + 6000x
c) gewinnmaximale Menge 48,30 ME p(48,30)= 3102 Gewinn: 82710,72
d) E(x)=2044x und G(x)= - 0,5x^3 + 60x^2 – 456x – 30000
Neues Gewinnmaximum: (76 |62416)
4. Im Angebotsmonopol sei der Höchstpreis 10 € und die Sättigungsmenge 100 ME. Die
Gesamtkosten (lineare Kostenfunktion) die zu den Ausbringungsmengen x1 = 20 und x2 = 60 gehören
sind 130 € und 190 €.
a) Stellen Sie die PAF, die Erlös und die Gesamtkostenfunktion auf..
b) Berechnen Sie die Cournotsche Menge, den Cournotschen Punkt und den Monopolgewinn.
c) Wie wirkt sich eine Veränderung der fixen Kosten um h € auf den Monopolgewinn aus?
d) Wie wirkt sich eine Veränderung der variablen Kosten um h € auf die Cournotsche Menge, den
Preis und den Gewinn aus?
Lösungen:
a) p(x) = -0,1x+10 E(x) = ? K(x) = 1,5x + 100
5. Ein Betrieb stellt Werkzeuge her. In der Planperiode fallen fixe Kosten von 2100 € und variable
Kosten von 280 € je 10 produzierte Einheiten an. Der Verkaufspreis beträgt 78 €.
a) Berechnen Sie die Nutzenschwelle.
b) Um welchen Betrag müsste der Stückpreis über dem proportionalen Satz liegen, wenn bereits bei
einer Absatzmenge von 35 ME die Gesamtkosten gedeckt sein sollen.
c) Berechnen Sie den maximalen Gewinn. (Die maximale Produktionsmenge beträgt 100
ME/Periode.)
d) Um welchen Betrag erhöht sich der Gewinn bzw. der Stückgewinn, wenn die Produktion auf 105
ME/Periode gesteigert werden kann?
6. Bestimmen Sie die lineare Gesamtkostenfunktion eines Monopolisten, wenn die Nutzenschwelle bei
8 ME und die Nutzengrenze bei 62 ME erreicht werden. Die Nachfragefunktion wird durch
p(x) = - 2x + 200 festgelegt.
Berechnen Sie gewinnmaximale Absatzmenge und Monopolgewinn.