DOCX

Formeln zur Höheren
Mathematik I
Lehrveranstaltungskopien ET/IKT/CSB
Inhaltsverzeichnis
1. Grundlagen .................................................................................... 4
1.1
Besondere Folgen 𝒂𝒌 und Reihen 𝒔𝒏 .................................................... 4
1.2
Elementare Aussagenverknüpfungen (Junktoren) der Formalen Logik .. 5
1.3
Komplexe Zahlen ................................................................................... 5
1.3.1
Darstellungsformen .............................................................................................. 5
1.3.2
Eulersche Formel .................................................................................................. 5
1.4
Trigonometrische und hyperbolische Funktionen .................................. 6
1.4.1
Winkelfunktionen ................................................................................................. 6
1.4.2
Additionstheoreme .............................................................................................. 7
1.4.3
Hyperbelfunktionen ............................................................................................. 7
1.5
Wichtige Eigenschaften von Funktionen ................................................ 8
2. Algebra .......................................................................................... 9
2.1
Vektoralgebra ........................................................................................ 9
2.2
Kurven und Flächen 2. Ordnung ........................................................... 10
3. Differentialrechnung ................................................................... 14
3.1
Grundformeln der Differentialrechnung .............................................. 14
3.1.1
Differentiationsregeln ........................................................................................ 14
3.1.2
Grundableitungen .............................................................................................. 14
3.2
Taylor-Approximation 𝑻𝒏𝒙 in 𝒙𝟎 für eine Funktion 𝒚 = 𝒇𝒙 ................ 15
3.3
Tabelle Taylor-Reihen .......................................................................... 16
4. Integralrechnung ......................................................................... 17
4.1
Grundformeln der Integralrechnung .................................................... 17
4.1.1
Integrationsregeln .............................................................................................. 17
4.1.2
Grundintegrale (ohne C)..................................................................................... 17
4.2
Geometrische Anwendung der Integralrechnung ................................ 18
5. Reihen ......................................................................................... 20
5.1
Zahlenreihen und Potenzreihen ........................................................... 20
5.1.1
Zahlenreihen....................................................................................................... 20
5.1.2
Potenzreihen ...................................................................................................... 20
5.2
Fourier-Reihen zu 𝒚 = 𝒇𝒙 mit Periode 𝑻 = 𝟐𝒑 ................................... 21
2
5.3
Tabelle Fourier-Reihen ......................................................................... 22
6. Laplace-Transformation .............................................................. 23
6.1
ET-Standardsignale .............................................................................. 23
6.2
Abbildungsgesetze der Laplace-Transformation 𝓛𝒇𝒕 = 𝑭𝒑 ................. 25
6.3
Stationäres Übertragungsverhalten von 𝑿𝒂𝒑 = 𝑮𝒑 ⋅ 𝑿𝒆𝒑 𝐑𝐞𝒑𝒌 < 0 26
6.4
Korrespondenztabelle zur Laplace-Transformation.............................. 26
7. Differentialgleichungen ............................................................... 28
7.1
DGL-Lösungsmethoden ........................................................................ 28
7.1.1
Trennung der Variablen ..................................................................................... 28
7.1.2
Allgemeine Lineare DGL 1. Ordnung .................................................................. 28
7.1.3
Lineare DGL mit konstanten Koeffizienten ........................................................ 28
3
1.
Grundlagen
1.1
Besondere Folgen 𝒂𝒌 und Reihen 𝒔𝒏
Arithmetische Folge: 𝑎𝑘+1 = 𝑎𝑘 + 𝑑 bzw. 𝑎𝑘 = 𝑎1 + (𝑘 − 1)𝑑 (d: konstante Differenz)
Arithmetische Reihe:
𝑛
𝑛
1
𝑠𝑛 = ∑ 𝑎𝑘 = (𝑎1 + 𝑎𝑛 ) = 𝑛𝑎1 + 𝑛(𝑛 − 1)𝑑
2
2
𝑘=1
Logik:
𝑠𝑛 = 𝑎1 + (𝑎1 + 𝑑) + ⋯ + (𝑎𝑛 − 𝑑) + 𝑎𝑛
} ⊕: 2𝑠𝑛 = 𝑛 ⋅ (𝑎1 + 𝑎𝑛 )
𝑠𝑛 = 𝑎𝑛 + (𝑎𝑛 − 𝑑) + ⋯ + (𝑎1 + 𝑑 ) + 𝑎1
z.B. Unterjährige Verzinsung (Stückzins), Technologische Stufungen (relativ selten, z.B.
Spannungsregler), Gleichförmige Bewegungen
Geometrische Folge: 𝑎𝑘+1 = 𝑎𝑘 ⋅ 𝑞 bzw. 𝑎𝑘 = 𝑎1 ⋅ 𝑞 𝑘−1 (q: konstanter Quotient)
Geometrische Reihe:
𝑛
𝑞𝑛 − 1
𝑎1
𝑠𝑛 = ∑ 𝑎𝑘 = 𝑎1 ⋅
; 𝑠∞ = lim 𝑠𝑛 =
für |𝑞| < 1
𝑛→∞
𝑞−1
1−𝑞
𝑘=1
Logik:
𝑠𝑛 = 𝑎1 + 𝑎1 ⋅ 𝑞 + 𝑎1 ⋅ 𝑞 2 + ⋯ + 𝑎1 ⋅ 𝑞 𝑛−1
} ⊖ : (𝑞 − 1)𝑠𝑛 = 𝑎1 (𝑞 𝑛 − 1)
𝑞 ⋅ 𝑠𝑛 = 𝑎1 ⋅ 𝑞 + 𝑎1 ⋅ 𝑞 2 + ⋯ + 𝑎1 ⋅ 𝑞 𝑛−1 + 𝑎1 ⋅ 𝑞 𝑛
z.B. Zinseszinsrechnung (Kapitalprobleme), Wachstums-, Abkling-, Zerfallsprozesse, eFunktionen, Technologische Stufungen (meistens, z.B. Rundwertreihen), gleichmäßig
beschleunigte Bewegung
Vergleich:
Arithmetische Stufung
a1
d
d
a2
Geometrische Stufung
d
a3
ϕ
a4 …
a1 a2 a3
𝑑 = 𝑎𝑛+1 − 𝑎𝑛
a4
𝜑
𝑎𝑛+1 1 + sin 2
𝑞=
=
𝜑
𝑎𝑛
1 − sin 2
𝜑 𝑎𝑛+1 − 𝑎𝑛
𝑎𝑛 + 𝑎𝑛+1
sin =
2 𝑎𝑛+1 + 𝑎𝑛
𝑎𝑛+1 − 𝑎𝑛
4
1.2
Elementare Aussagenverknüpfungen (Junktoren) der
Formalen Logik
Name
Negation
Alternative
(Disjunktion)
Konjunktion
Abkürzung Symbolik
NOT, non 𝑝, ¬𝑝, ~𝑝
Implikation
IMP, seq
Äquivalenz
AEQ, aeq
Antivalenz
XOR, ant
OR, vel
𝑝 ∨ 𝑞, +
AND, et
𝑝 ∧ 𝑞, ·, &
Formulierungen
nicht p, p quer
p oder (auch) q (nicht ausschließend)
p und q
aus p folgt q
wenn p, so q
𝑝 → 𝑞, ↷, ⇒
p ist hinreichend für q
q ist notwendig für p
aus p folg q und umgekehrt
𝑝 ⟷ 𝑞,
, ⟺, ∼, = p genau dann, wenn q
p ist notwendig und hinreichend für q
entweder p oder q
𝑝 >—< 𝑞, ≁
p kontra q
Wahrheitswerttabelle:
p q 𝑝 𝑝∨𝑞
w w f
w
w f f
w
f w w
w
f f w
f
1.3
𝑝∧𝑞
w
f
f
f
𝑝→𝑞
w
f
w
w
𝑝⟷𝑞
w
f
f
w
𝑝 >— < 𝑞
f
w
w
f
Komplexe Zahlen
1.3.1 Darstellungsformen
Arithmetische Form: 𝑧 = 𝑥 + 𝑗𝑦 (𝑥 = Re 𝑧 , 𝑦 = Im 𝑧)
Trigonometrische Form: 𝑧 = 𝑟(cos 𝜑 + 𝑗 sin 𝜑)
Exponentialform: 𝑧 = 𝑟𝑒 𝑗𝜑 (𝑟 = |𝑧|, 𝜑 = arg 𝑧)
Umrechnungen Kartesische Koordinaten ⇔ Polarkoordinaten:
𝑦
(𝑥, 𝑦) ⟹ (𝑟, 𝜑) ∶ 𝑟 = √𝑥 2 + 𝑦 2 , tan 𝜑 =
𝑥
(𝑟, 𝜑) ⟹ (𝑥, 𝑦) ∶ 𝑥 = 𝑟 cos 𝜑 , 𝑦 = 𝑟 sin 𝜑
1.3.2 Eulersche Formel
𝑒 ±𝑗𝜑 = cos 𝜑 ± 𝑗 sin 𝜑
⟶ (cos 𝜑 + 𝑗 sin 𝜑)𝑛 = cos 𝑛𝜑 + 𝑗 sin 𝑛𝜑 Moivrescher Satz
konjugiert komplexe Zahl: 𝑧 = 𝑥 − 𝑗𝑦 = 𝑟(cos 𝜑 − 𝑗 sin 𝜑) = 𝑟𝑒 −𝑗𝜑 (= 𝑧 ∗ )
5
Rechenoperation
arithmetisch exponentiell grafisch
Addition/Subtraktion
⊕
⊕
Multiplikation/Division
+
+
∅
Potenzieren
∅
⊕
Radizieren
⊕
j-Potenzen:
𝑗 = 𝑗 = 𝑗 4𝑔+1
𝑗 2 = −1 = 𝑗 4𝑔+2
𝑔=−1
𝑗 3 = −𝑗 = 𝑗 4𝑔+3 →
1
= −𝑗
𝑗
𝑗 4 = 1 = 𝑗 4𝑔
1.4
Trigonometrische und hyperbolische Funktionen
Gradmaß ⇔ Bogenmaß:
180°
𝜋
𝜑° =
⋅ 𝜑̂ ⟺ 𝜑̂ =
⋅ 𝜑° (𝜑̂ = arc 𝜑°)
𝜋
180°
1.4.1 Winkelfunktionen
sin 𝜑 =
H
𝐺𝐾
𝐻
ϕ
cos 𝜑 =
𝐴𝐾
𝐻
tan 𝜑 =
𝐺𝐾
𝐴𝐾
cot 𝜑 =
𝐴𝐾
𝐺𝐾
GK
AK
sin2 𝜑 + cos2 𝜑 = 1
tan 𝜑 =
𝜑°
0°
𝜑̂
0
sin 𝜑
→
←
cos 𝜑
cot 𝜑
30°
𝜋
6
45°
𝜋
4
60°
𝜋
3
90°
𝜋
2
1
1
1 1
1
1
√0 = 0
√1 =
√2
√3
√4 = 1
2
2
2 2
2
2
tan 𝜑
→
←
sin 𝜑
1
=
cos 𝜑 cot 𝜑
0
1
1
√3
6
√3
∞
cot ϕ
tan ϕ
sin ϕ
ϕ°
arc ϕ
cos ϕ
1.4.2 Additionstheoreme
sin(𝛼 ± 𝛽) = sin 𝛼 cos 𝛽 ± cos 𝛼 sin 𝛽 cos(𝛼 ± 𝛽) = cos 𝛼 cos 𝛽 ∓ sin 𝛼 sin 𝛽
sin 2𝛼 = 2 sin 𝛼 cos 𝛼
cos 2𝛼 = cos 2 𝛼 − sin2 𝛼
1
(1 − cos 2𝛼)
2
𝑥+𝑦
𝑥−𝑦
sin 𝑥 + sin 𝑦 = 2 sin
cos
2
2
𝑥+𝑦
𝑥−𝑦
sin 𝑥 − sin 𝑦 = 2 cos
sin
2
2
1
cos 2 𝛼 = (1 + cos 2𝛼)
2
𝑥+𝑦
𝑥−𝑦
cos 𝑥 + cos 𝑦 = 2 cos
cos
2
2
𝑥+𝑦
𝑥−𝑦
cos 𝑥 − cos 𝑦 = −2 sin
sin
2
2
sin2 𝛼 =
1.4.3 Hyperbelfunktionen
1 𝑥
(𝑒 − 𝑒 −𝑥 ) arsinh 𝑥 = ln (𝑥 + √𝑥 2 + 1)
2
1
cosh 𝑥 = (𝑒 𝑥 + 𝑒 −𝑥 ) arcosh 𝑥 = ln (𝑥 + √𝑥 2 − 1) |𝑥| ≥ 1
2
cosh2 𝑥 − sinh2 𝑥 = 1
sinh 𝑥 =
tanh 𝑥 =
sinh 𝑥
cosh 𝑥
coth 𝑥 =
1
tanh 𝑥
7
1.5
Wichtige Eigenschaften von Funktionen
Monotonie:
𝑥1 < 𝑥2 ↷ 𝑓(𝑥1 ) ≤ 𝑓(𝑥2 )
⇒ monoton wachsend
Beschränktheit:
obere Schranken
Symmetrie:
𝑓(−𝑥) = 𝑓(𝑥) ⇒ gerade
𝑓(−𝑥) = −𝑓(𝑥) ⇒ ungerade
Periodizität
𝑓(𝑥 + 𝑃) = 𝑓(𝑥)
P
Koordinatenverschiebung:
𝑦 = 𝑓(𝑥) ⇔ 𝑦 − 𝑏 = 𝑓(𝑥 − 𝑎)
y
y
b
x
x
a
Umkehrung:
grafisch:
analytisch:
𝑥↔𝑦
𝑦 = 𝑓(𝑥) →
y=f(x)
𝑥 = 𝑓(𝑦) ⇔ 𝑦 = 𝑓 −1 (𝑥)
y=x
y=f-1(x)
Wichtige Punkte und Verhalten von Funktionen:
y
E
P
E
N
y=f(x)
W
x
N: Nullstelle 𝑓(𝑥𝑁 ) = 0
E: Extremwert (Max, Min)
W: Wendepunkt (konvex – konkav)
P: Polstelle 𝑓(𝑥𝑃 ) = ±∞
A: Asymptote 𝑥 → ±∞ ∶ 𝑦 → 𝑦𝐴
A
A
8
2.
Algebra
2.1
Vektoralgebra
Ortsvektor:
𝑥
⃗⃗ 𝑟 = |𝑟⃗| = √𝑥 2 + 𝑦 2 + 𝑧 2
𝑦
𝑟⃗ = ( ) = 𝑥𝑖⃗ + 𝑦𝑗⃗ + 𝑧𝑘
𝑧
Skalarprodukt:
𝑒𝑟 =
⃗⃗⃗⃗
𝑟⃗
(|𝑒⃗⃗⃗⃗|
𝑟 = 1)
|𝑟⃗|
r2
ϕ
r1
𝑟⃗⃗⃗⃗1 ⋅ ⃗⃗⃗⃗
𝑟2 = |𝑟⃗⃗⃗⃗|
⃗⃗⃗⃗|
1 ⋅ |𝑟
2 ⋅ cos 𝜑 = 𝑥1 𝑥2 + 𝑦1 𝑦2 + 𝑧1 𝑧2
(𝑟⃗ ⋅ 𝑟⃗ = 𝑟⃗ 2 = |𝑟⃗|2 = 𝑥 2 + 𝑦 2 + 𝑧 2 ⃗⃗⃗⃗
𝑟1 ⋅ ⃗⃗⃗⃗
𝑟2 = 0 ↔ ⃗⃗⃗⃗
𝑟1 ⊥ ⃗⃗⃗⃗)
𝑟2
Vektorprodukt:
r1 x r2
r2
A
ϕ
r1
⃗⃗
𝑘
𝑟2 = |𝑟⃗⃗⃗⃗|
⃗⃗⃗⃗|
𝑧1 | |𝑟⃗⃗⃗⃗1 × ⃗⃗⃗⃗|
1 ⋅ |𝑟
2 sin 𝜑 = 𝐴
𝑧2
⃗⃗⃗⃗
𝑟1 × ⃗⃗⃗⃗
𝑟2 = ⃗⃗
0 ↔ ⃗⃗⃗⃗
𝑟1 ∥ ⃗⃗⃗⃗)
𝑟2
𝑖⃗
𝑗⃗
𝑟1 × ⃗⃗⃗⃗
⃗⃗⃗⃗
𝑟2 = |𝑥1 𝑦1
𝑥2 𝑦2
(𝑟⃗⃗⃗⃗1 × ⃗⃗⃗⃗
𝑟2 = −𝑟⃗⃗⃗⃗2 × ⃗⃗⃗⃗
𝑟1
Spatprodukt:
𝑥1
[𝑟⃗⃗⃗⃗1 ⃗⃗⃗⃗
𝑟2 ⃗⃗⃗⃗]
𝑟3 = ⃗⃗⃗⃗
𝑟1 ⋅ (𝑟⃗⃗⃗⃗2 × ⃗⃗⃗⃗)
𝑟3 = (𝑟⃗⃗⃗⃗1 × ⃗⃗⃗⃗)
𝑟2 ⋅ ⃗⃗⃗⃗
𝑟3 = |𝑥2
𝑥3
|[𝑟⃗⃗⃗⃗1 𝑟⃗⃗⃗⃗2 ⃗⃗⃗⃗]|
𝑟3 = 𝑉Spat = 6 ⋅ 𝑉Tetr.
𝑦1
𝑦2
𝑦3
𝑧1
𝑧2 |
𝑧3
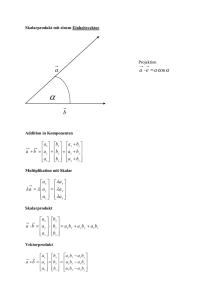
Orthogonalprojektion:
n
v
ϕ
vm
vn
m
Abstände
Fußpunkte
𝑣𝑚 = 𝑣 ⋅ cos 𝜑 = 𝑣
⃗⃗ ⋅ ⃗⃗⃗⃗⃗
𝑒𝑚
𝑣𝑚 = (𝑣
⃗⃗⃗⃗⃗
⃗⃗ ⋅ ⃗⃗⃗⃗⃗)
𝑒𝑚 ⃗⃗⃗⃗⃗
𝑒𝑚
𝑣𝑛 = 𝑣 ⋅ sin 𝜑 = |𝑣
⃗⃗ × ⃗⃗⃗⃗⃗|
𝑒𝑚 = √𝑣2 − 𝑣2𝑚
𝑣𝑛 = 𝑣
⃗⃗⃗⃗
⃗⃗ − ⃗⃗⃗⃗⃗
𝑣𝑚 = 𝑣𝑛 ⃗⃗⃗⃗
𝑒𝑛
9
Geraden:
g
n
m
r
r0
0
𝑟⃗ = ⃗⃗⃗⃗
𝑟0 + 𝑡 ⋅ 𝑚
⃗⃗⃗ (ℝ2 , ℝ3 )
(𝑟⃗ − ⃗⃗⃗⃗)
𝑟0 ⋅ 𝑛⃗⃗ = 0 (ℝ2 )
(𝑟⃗ − ⃗⃗⃗⃗)
𝑟0 × 𝑚
⃗⃗⃗ = ⃗0⃗ (ℝ2 , ℝ3 )
Ebenen:
m2
n
E
m1
r0
r
0
𝑟⃗ = ⃗⃗⃗⃗
𝑟0 + 𝑠 ⋅ ⃗⃗⃗⃗⃗⃗
𝑚1 + 𝑡 ⋅ ⃗⃗⃗⃗⃗⃗
𝑚2
3
(𝑟⃗ − ⃗⃗⃗⃗)
𝑟0 ⋅ 𝑛⃗⃗ = 0 (ℝ )
[(𝑟⃗ − ⃗⃗⃗⃗),
𝑟0 ⃗⃗⃗⃗⃗⃗,
𝑚1 ⃗⃗⃗⃗⃗⃗]
𝑚2 = 0
2.2
Kurven und Flächen 2. Ordnung
2D-Grundgleichungen (Kegelschnitte)
Kreis
𝑥2 + 𝑦2 = 𝑟2
y
x
r
Ellipse
𝑥2 𝑦2
+
=1
𝑎2 𝑏 2
y
b
x
a
Parabel
𝑥 2 = 2𝑝𝑦
𝑝
(𝑆𝐹 = )
2
y
F
x
S
10
Hyperbel
y
y
𝑥2 𝑦2
−
=1
𝑎2 𝑏 2
b
x
a
b
x
a
y
b
x
a
3D-Grundgleichungen
Flächen über 2D-Grundgleichungen (Niveau-Kurven) vorstellbar (→ „Drahtgitter-Modell“)
Ellipsoid
𝑥2 𝑦2 𝑧2
+
+ =1
𝑎2 𝑏 2 𝑐 2
z
c
a
b
y
x
elliptisches Paraboloid
𝑥2 𝑦2
+
=𝑧
𝑎2 𝑏 2
z
y
x
hyperbolisches Paraboloid
𝑥2 𝑦2
−
=𝑧
𝑎2 𝑏 2
z
y
x
11
einschaliges Hyperboloid
𝑥2 𝑦2 𝑧2
+
− =1
𝑎2 𝑏 2 𝑐 2
z
zweischaliges Paraboloid
y
b
a
x
𝑥2 𝑦2 𝑧2
−
− =1
𝑎2 𝑏 2 𝑐 2
z
y
x
elliptischer Kegel
𝑥2 𝑦2 𝑧2
+
− =0
𝑎2 𝑏 2 𝑐 2
z
b
a
c
y
x
𝑥2 𝑦2
+
=1
𝑎2 𝑏 2
elliptischer Zylinder
z
y
x
12
hyperbolischer Zylinder
𝑥2 𝑦2
−
=1
𝑎2 𝑏 2
z
y
x
𝑦 2 = 2𝑝𝑥
parabolischer Zylinder
z
y
x
Allgemeine quadratische Form
𝑎11 𝑥 2 + 𝑎22 𝑦 2 + 𝑎33 𝑧 2 + 2𝑎12 𝑥𝑦 + ⋯ + 𝑏1 𝑥 + ⋯ + 𝑐 = 0
𝑥⃗ 𝑇 ⋅ 𝐴 ⋅ 𝑥⃗ + 𝑏⃗⃗ 𝑇 ⋅ 𝑥⃗ + 𝑐 = 0
Transformation 1 (Drehung)
2
2
2
𝑥⃗ = 𝐵 ⋅ 𝑥⃗ ′ ⟶ 𝜆1 𝑥 ′ + 𝜆2 𝑦 ′ + 𝜆3 𝑧 ′ + 𝑏⃗⃗ 𝑇 ⋅ 𝐵 ⋅ 𝑥⃗ ′ + 𝐶 = 0
𝜆1
|𝐵| = +1 (Rechtssystem) 𝐵 ⋅ 𝐴 ⋅ 𝐵 = (
𝐵 = (𝑒
⃗⃗⃗⃗,
𝑒2 𝑒⃗⃗⃗⃗)
1 ⃗⃗⃗⃗,
3
0
𝑇
Transformation 2 (Verschiebung)
′
𝑥⃗ ′′ = 𝑥⃗ ′ − ⃗⃗⃗⃗⃗
𝑥0
2D-Vorstellung
y‘
y
e2
y‘‘
e1
x‘‘
x‘
x
13
0
𝜆2
)
𝜆3
3.
Differentialrechnung
3.1
Grundformeln der Differentialrechnung
3.1.1 Differentiationsregeln
konstanter Summand: [𝑐 + 𝑓(𝑥)]′ = 𝑓 ′ (𝑥)
konstanter Faktor:
[𝑐 ⋅ 𝑓(𝑥)]′ = 𝑐 ⋅ 𝑓 ′ (𝑥)
Summe/Differenz:
[𝑢(𝑥) ± 𝑣(𝑥)]′ = 𝑢′ ± 𝑣 ′
Produkt:
[𝑢(𝑥) ⋅ 𝑣(𝑥)]′ = 𝑢′ ⋅ 𝑣 + 𝑢 ⋅ 𝑣 ′
Quotient:
𝑢 ′ 𝑢′ ⋅ 𝑣 − 𝑢 ⋅ 𝑣 ′
[ ] =
𝑣
𝑣2
1′
𝑣′
[ ] = − 2 oder [𝑣 −1 ]′ = (−1) ⋅ 𝑣 −2 ⋅ 𝑣 ′
𝑣
𝑣
𝑑𝑓 𝑑𝑓 𝑑𝑢
′
=
⋅
= 𝑓 ′ (𝑢) ⋅ 𝑢′ (𝑥)
[𝑓(𝑢(𝑥))] =
𝑑𝑥 𝑑𝑢 𝑑𝑥
= äußere Ableitung · innere Ableitung
Kehrwert:
Verkettung:
Implizit:
′
[𝑓(𝑦(𝑥))] =
𝑑𝑓(𝑦) 𝑑𝑦
⋅
𝑑𝑦 𝑑𝑥
Bsp. : 𝑦 = arctan 𝑥 , (tan 𝑦 = 𝑥)′ ⟶ (1 + tan2 𝑦) ⋅ 𝑦 ′ = 1 ⟶ 𝑦 ′ =
3.1.2 Grundableitungen
Potenz-Funktion:
(𝑥 𝑟 )′ = 𝑟 ⋅ 𝑥 𝑟−1
Exponential-Funktion:
(𝑒 𝑥 )′ = 𝑒 𝑥 (𝑎 𝑥 )′ = 𝑎 𝑥 ln 𝑎 Vgl.: 𝑎 𝑥 = 𝑒 𝑥 ln 𝑎
1
1
ln 𝑥
(log 𝑎 𝑥)′ =
Vgl.: log 𝑎 𝑥 =
𝑥
𝑥 ln 𝑎
ln 𝑎
′
′
Trigonometrische Funktionen: (sin 𝑥) = cos 𝑥 (cos 𝑥) = − sin 𝑥
1
(tan 𝑥)′ =
= 1 + tan2 𝑥
cos2 𝑥
1
(cot 𝑥)′ = − 2 = −(1 + cot 2 𝑥)
sin 𝑥
1
Arcus-Funktionen:
(arcsin 𝑥)′ =
= −(arccos 𝑥)′ (|𝑥| < 1)
(Zyklom.)
√1 − 𝑥 2
1
(arctan 𝑥)′ =
= −(arccot 𝑥)′
1 + 𝑥2
(sinh 𝑥)′ = cosh 𝑥 (cosh 𝑥)′ = sinh 𝑥
Hyperbel-Funktionen:
1
(tanh 𝑥)′ =
= 1 − tanh2 𝑥
cosh2 𝑥
1
(coth 𝑥)′ = −
= 1 − coth2 𝑥
sinh2 𝑥
Logarithmus-Funktion:
(ln 𝑥)′ =
14
1
1 + 𝑥2
Area-Funktionen:
(arsinh 𝑥)′ =
1
(arcosh 𝑥)′ =
√1 + 𝑥 2
1
(artanh 𝑥)′ =
(|𝑥| < 1)
1 − 𝑥2
1
(arcoth 𝑥)′ =
(|𝑥| > 1)
1 − 𝑥2
3.2
1
√𝑥 2 − 1
(|𝑥| > 1)
Taylor-Approximation 𝑻𝒏 (𝒙) in 𝒙𝟎 für eine Funktion
𝒚 = 𝒇(𝒙)
𝑓 ′ (𝑥0 )
𝑓 (𝑛) (𝑥0 )
𝑓 (𝑛+1) (𝜉)
𝑛
(𝑥 − 𝑥0 ) + ⋯ +
(𝑥 − 𝑥0 ) +
(𝑥 − 𝑥0 )𝑛+1
𝑓(𝑥) = 𝑓(𝑥0 ) +
⏟
(𝑛 + 1)!
1!
𝑛!
⏟
Polynom 𝑇𝑛 (𝑥)
𝑛→∞
𝑛→∞
Restglied 𝑅𝑛 (𝑥) (𝑥0 …𝜉…𝑥)
Theoretisches Problem: 𝑇𝑛 (𝑥) → 𝑓(𝑥) ?, d.h. 𝑅𝑛 (𝑥) → 0 ?
Praktisches Problem: Für welche kleine n und 𝑥 ≈ 𝑥0 gilt 𝑇𝑛 (𝑥) ≈ 𝑓(𝑥) ausreichend gut?
𝑥0 bel
Bsp. 1: 𝑒 𝑥 = 𝑒 𝑥0 + 𝑒 𝑥0 (𝑥 − 𝑥0 ) + ⋯ +
𝑒 𝑥0
𝑒𝜉
(𝑥 − 𝑥0 )𝑛 +
(𝑥 − 𝑥0 )𝑛+1
(𝑛 + 1)!
𝑛!
für 𝑥 ∈ (−∞, ∞) konvergent
𝑥 =0
𝑥2
𝑥𝑛
𝑒𝜉
𝑥 0
speziell: 𝑒 = 1 + 𝑥 + + ⋯ +
+
𝑥 𝑛+1
(𝑛
2
𝑛!
+ 1)!
(|𝑥| < 0,044)
𝑒𝑥 ≈ 1 + 𝑥
2
(|𝑅
|
praktisch
𝑥
𝑛 < 0,001): 𝑥
(|𝑥| < 0,17)
𝑒 ≈ 1+𝑥+
2
𝑥2 𝑥4
Bsp. 2: cos 𝑥 = 1 − + ∓ ⋯ für 𝑥 ∈ (−∞, ∞) konvergent
2! 4!
𝑥2
(|𝑥| < 0,394 =
praktisch: (|𝑅𝑛 | < 0,001): cos 𝑥 ≈ 1 −
̂ 22,6°)
2
𝑥0 =0
𝑥0 =0
𝛼
𝛼
Bsp. 3: (1 + 𝑥)𝛼 = 1 + ( ) 𝑥 + ( ) 𝑥 2 + ⋯ (verallgemeinerter binomischer Satz) für 𝑥 ∈
1
2
(−1, 1) konvergent
1
z.B. 1+𝑥 = 1 − 𝑥 + 𝑥 2 − 𝑥 3 ± ⋯ (geometrische Reihe mit 𝑞 = −𝑥)
𝑥
⇒∫
0
1
𝑥2 𝑥3
𝑑𝑥 = ln(1 + 𝑥) = 𝑥 − + ∓ ⋯
1+𝑥
2
3
1 ′
1
(
) =−
= −1 + 2𝑥 − 3𝑥 2 ± ⋯
(1 + 𝑥)2
1+𝑥
1
praktisch (|𝑥| ≪ 1): (1 + 𝑥)𝛼 ≈ 1 + 𝛼𝑥 √1 + 𝑥 ≈ 1 + 𝑥
2
1
≈ 1 − 𝑥 ln(1 + 𝑥) ≈ 𝑥
1+𝑥
𝛼
𝛼
𝑥2
𝑥2
𝛼𝑥 2
𝛼
𝛼
Bsp.4: für |𝑥| ≪ 1 ist: (1 + cos 𝑥) ≈
⏟ (2 − ) = 2 (1 − ) ≈
⏟ 2𝛼 (1 −
)
2
4
4
Bsp.2
Bsp.3
(mehrfache T-Approximation)
15
3.3
Tabelle Taylor-Reihen
∞
𝒙 𝒙𝟐 𝒙𝟑
𝒙𝒏
𝒙
𝒆 =𝟏+ + + +⋯= ∑
𝟏! 𝟐! 𝟑!
𝒏!
𝒏=𝟎
𝑥2
(|𝑥| ≤ 0,17)
𝐴1: 𝑒 ≈ 1 + 𝑥 (|𝑥| ≤ 0,044), 𝐴2: 𝑒 ≈ 1 + 𝑥 +
2
∞
𝒙𝟑 𝒙𝟓
𝒙𝟐𝒏+𝟏
𝒏
𝐬𝐢𝐧 𝒙 = 𝒙 − + ∓ ⋯ = ∑(−𝟏)
(𝟐𝒏 + 𝟏)!
𝟑! 𝟓!
𝑥
𝑥
𝒏=𝟎
𝐴1: sin 𝑥 ≈ 𝑥 (|𝑥| ≤ 0,18 = 10,4°), 𝐴2: sin 𝑥 ≈ 𝑥 −
∞
𝑥3
(|𝑥| ≤ 0,63 = 36°)
6
𝒙𝟐 𝒙𝟒
𝒙𝟐𝒏
𝒏
𝐜𝐨𝐬 𝒙 = 𝟏 − + ∓ ⋯ = ∑(−𝟏)
(𝟐𝒏)!
𝟐! 𝟒!
𝒏=𝟎
𝑥2
(|𝑥|
(|𝑥| ≤ 0,394 = 22,6°)
𝐴1: cos 𝑥 ≈ 1
≤ 0,044 = 2,6°), 𝐴2: cos 𝑥 ≈ 1 −
2
𝟏
𝟐 𝟓
𝟏𝟕 𝟕
𝝅
𝐭𝐚𝐧 𝒙 = 𝒙 + 𝒙𝟑 +
𝒙 +
𝒙 + ⋯ konvergent |𝒙| <
𝟑
𝟏𝟓
𝟑𝟏𝟓
𝟐
𝑥3
(|𝑥| ≤ 0,38 = 21,6°)
𝐴1: tan 𝑥 ≈ 𝑥 (|𝑥| ≤ 0,14 = 8,2°), 𝐴2: tan 𝑥 ≈ 𝑥 +
3
∞
𝒙𝟑 𝒙𝟓
𝒙𝟐𝒏+𝟏
𝐬𝐢𝐧𝐡 𝒙 = 𝒙 + + + ⋯ = ∑
(𝟐𝒏 + 𝟏)!
𝟑! 𝟓!
𝒏=𝟎
𝐴1: sinh 𝑥 ≈ 𝑥 (|𝑥| ≤ 0,18), 𝐴2: sinh 𝑥 ≈ 𝑥 +
∞
𝑥3
(|𝑥| ≤ 0,65)
6
𝒙𝟐 𝒙𝟒
𝒙𝟐𝒏
𝐜𝐨𝐬𝐡 𝒙 = 𝟏 + + + ⋯ = ∑
(𝟐𝒏)!
𝟐! 𝟒!
𝒏=𝟎
𝑥2
(|𝑥| ≤ 0.39)
𝐴1: cosh 𝑥 ≈ 1 (|𝑥| ≤ 0,044) 𝐴2: cosh 𝑥 ≈ 1 +
2
𝟏
𝟐 𝟓
𝟏𝟕 𝟕
𝝅
𝐭𝐚𝐧𝐡 𝒙 = 𝒙 − 𝒙𝟑 +
𝒙 −
𝒙 ± ⋯ konvergent |𝒙| <
𝟑
𝟏𝟓
𝟑𝟏𝟓
𝟐
𝑥3
(|𝑥| ≤ 0,32)
𝐴1: tanh 𝑥 ≈ 𝑥 (|𝑥| ≤ 0,14), 𝐴2: tanh 𝑥 ≈ 𝑥 −
3
𝟏 𝒙𝟑 𝟏 ⋅ 𝟑 𝒙𝟓 𝟏 ⋅ 𝟑 ⋅ 𝟓 𝒙𝟕
𝐚𝐫𝐜𝐬𝐢𝐧 𝒙 = 𝒙 + ⋅ +
⋅ +
⋅ + ⋯ konvergent |𝒙| < 1
𝟐 𝟑 𝟐⋅𝟒 𝟓 𝟐⋅𝟒⋅𝟔 𝟕
𝑥3
(|𝑥| ≤ 0,42)
𝐴1: arcsin 𝑥 ≈ 𝑥 (|𝑥| ≤ 0,18), 𝐴2: arcsin 𝑥 ≈ 𝑥 +
6
𝒙𝟑 𝒙𝟓 𝒙𝟕
𝐚𝐫𝐜𝐭𝐚𝐧 𝒙 = 𝒙 − + − ± ⋯ konvergent − 1 < 𝑥 ≤ 1
𝟑
𝟓
𝟕
𝑥3
(|𝑥| ≤ 0,35)
𝐴1: arctan 𝑥 ≈ 𝑥 (|𝑥| ≤ 0,14), 𝐴2: arctan 𝑥 ≈ 𝑥 −
3
𝒙𝟐 𝒙 𝟑 𝒙𝟒
𝐥𝐧(𝟏 + 𝒙) = 𝒙 − + − ± ⋯ konvergent − 1 < 𝑥 ≤ 1
𝟐
𝟑
𝟒
𝑥2
(|𝑥| ≤ 0,14)
𝐴1: ln(1 + 𝑥) ≈ 𝑥 (|𝑥| < 0,044), 𝐴2: ln(1 + 𝑥) ≈ 𝑥 −
2
𝟏
= 𝟏 ∓ 𝒙 + 𝒙𝟐 ∓ 𝒙𝟑 … konvergent |𝒙| < 1
𝟏±𝒙
16
𝟏
𝟏
𝜶
𝜶
𝜶
(𝟏 ± 𝒙)𝜶 = 𝟏 ± ( ) 𝒙 + ( ) 𝒙𝟐 ± ( ) 𝒙𝟑 … z.B. 𝜶 = ; − ; −𝟐
𝟑
𝟏
𝟐
𝟐
𝟐
𝑛
𝑛
(Vgl. Binomischer Satz: (𝑎 + 𝑏)𝑛 = ∑ ( ) 𝑎𝑛−𝑘 𝑏 𝑘 )
𝑘
𝑘=0
4.
Integralrechnung
4.1
Grundformeln der Integralrechnung
4.1.1 Integrationsregeln
konstanter Summand:
∫ 𝐶 + 𝑓(𝑥)𝑑𝑥 = 𝐶 ⋅ 𝑥 + ∫ 𝑓(𝑥)𝑑𝑥
konstanter Faktor:
∫ 𝐶 ⋅ 𝑓(𝑥)𝑑𝑥 = 𝐶 ⋅ ∫ 𝑓(𝑥)𝑑𝑥
Summe/Differenz:
∫[𝑢(𝑥) ± 𝑣(𝑥)]𝑑𝑥 = ∫ 𝑢(𝑥)𝑑𝑥 ± ∫ 𝑣(𝑥)𝑑𝑥
partielle Integration:
∫ 𝑢′ ⋅ 𝑣𝑑𝑥 = 𝑢 ⋅ 𝑣 − ∫ 𝑢 ⋅ 𝑣 ′ 𝑑𝑥
Umkehrung der Produktregel:
(𝑢 ⋅ 𝑣)′ = 𝑢′ ⋅ 𝑣 + 𝑢 ⋅ 𝑣 ′
Integration durch Substitution:
∫ 𝑓(𝑢(𝑥)) ⋅ 𝑢′ (𝑥)𝑑𝑥 = 𝐹(𝑢(𝑥))
𝑑𝑡
= 𝑢′ (𝑥)
𝑑𝑥
Umkehrung der Verkettungs-Regel:
𝑑𝐹(𝑢(𝑥))
= 𝑓(𝑢(𝑥)) ⋅ 𝑢′ (𝑥)
𝑑𝑥
𝑍(𝑥)
∫
𝑑𝑥
𝑁(𝑥)
mit 𝑍(𝑥)/𝑁(𝑥) Polynome in x m-/n-ten Grades (𝑚 < 𝑛)

𝑁(𝑥) faktorisieren (reell, evtl. komplex)

Partialbrüche ansetzen (Koeffizienten 𝑐𝑖𝑘 )

𝑐𝑖𝑘 ermitteln, z.B. 𝑥𝑝 einsetzen und/oder x-Pot.-Vgl.

Partialbrüche integrieren
Sub: 𝑡 = 𝑢(𝑥),
Integration durch PBZ:
(Partialbruchzerlegung)
4.1.2 Grundintegrale (ohne C)
𝑥 𝑟+1
1
(𝑟 ≠ −1), ∫ 𝑑𝑥 = ln|𝑥|
𝑟+1
𝑥
𝑥
𝑎
∫ 𝑒 𝑥 𝑑𝑥 = 𝑒 𝑥 ∫ 𝑎 𝑥 𝑑𝑥 =
Vgl.: 𝑎 𝑥 = 𝑒 𝑥 ln 𝑎
ln 𝑎
∫ 𝑥 𝑟 𝑑𝑥 =
∫ sin 𝑥 𝑑𝑥 = − cos 𝑥
∫
∫ cos 𝑥 𝑑𝑥 = sin 𝑥
𝑑𝑥
= ∫(1 + tan2 𝑥)𝑑𝑥 = tan 𝑥
cos2 𝑥
∫
𝑑𝑥
= ∫(1 + cot 2 𝑥)𝑑𝑥 = − cot 𝑥
sin2 𝑥
17
𝑑𝑥
∫
= arcsin 𝑥 + 𝐶1 = − arccos 𝑥 + 𝐶2
√1 − 𝑥 2
𝑑𝑥
∫
= arctan 𝑥 + 𝐶1 = − arccot 𝑥 + 𝐶2
1 + 𝑥2
∫ sinh 𝑥 𝑑𝑥 = cosh 𝑥
∫
∫
𝑑𝑥
= tanh 𝑥
cosh2 𝑥
𝑑𝑥
√1 + 𝑥 2
4.2
∫ cosh 𝑥 𝑑𝑥 = sinh 𝑥
∫
𝑑𝑥
= − coth 𝑥
sinh2 𝑥
= arsinh 𝑥 = ln (𝑥 + √1 + 𝑥 2 ) ∫
𝑑𝑥
1+𝑥
(|𝑥| < 1)
= artanh 𝑥 = ln √
2
1−𝑥
1−𝑥
Geometrische Anwendung der Integralrechnung
Flächen
dA
A
𝑥2
𝑦𝑑𝑥
∫ 𝑦𝑑𝑥 (∫ 𝑦 ⋅ 𝑥̇ 𝑑𝑡)
𝑥1
x1
x2
𝑦2
𝑥𝑑𝑦
y2
∫ 𝑥𝑑𝑦 , 𝑥 = 𝑓 −1 (𝑦) (∫ 𝑥 ⋅ 𝑦̇ 𝑑𝑡)
y1
𝑦1
𝜑2
1 2
𝑟 𝑑𝜑
2
ϕ2
1
∫ 𝑟 2 𝑑𝜑
2
ϕ1
r
𝜑1
y
ϕ
x
1
→ (𝑥 2 + 𝑦 2 ) ⋅
2
t2
t1
1
⋅
𝑦 2
1 + (𝑥 )
𝑡2
𝑦̇ 𝑥 − 𝑦𝑥̇
𝑑𝑡
1
𝑥
𝑥2
∫|
𝑦
2
Beachte:
+
-
I1
I2
𝐴 = ∑|𝐼𝐾 |
𝐾
Längen
18
𝑡1
𝑥̇
| 𝑑𝑡
𝑦̇
𝑑𝑠 = √(𝑑𝑥)2 + (𝑑𝑦)2 → 𝑥 = 𝑟(𝜑) cos 𝜑 , 𝑦 = 𝑟(𝜑) sin 𝜑
𝑥2
𝜑2
𝑡2
𝑠 = ∫ √1 + 𝑦 ′ 2 𝑑𝑥
𝑠 = ∫ √𝑥̇ 2 + 𝑦̇ 2 𝑑𝑡
𝑥1
𝑠 = ∫ √𝑟 2 + 𝑟 ′ 2 𝑑𝜑
𝑡1
Volumina
dV
𝜋 ⋅ 𝑦 2 𝑑𝑥
𝜑1
V
𝑥2
𝜋 ⋅ ∫ 𝑦 2 𝑑𝑥
𝑥1
𝜋 ⋅ 𝑥 2 𝑑𝑦
𝑦2
𝜋 ⋅ ∫ 𝑥 2 𝑑𝑦
𝑦1
Oberflächen (nur Rotationskörper)
𝑑𝑂 = 2𝜋 ⋅ 𝑦𝑑𝑠
𝑥2
𝑂 = 2𝜋 ⋅ ∫ 𝑦 ⋅ √1 + 𝑦 ′ 2 𝑑𝑥
𝑥1
Integraler Mittelwert
y
x1
x2
𝑥2
𝑦 ⋅ (𝑥2 − 𝑥1 ) = ∫ 𝑦𝑑𝑥 (arithmetisch)
𝑥1
Numerische Integration
y0
x0
h
…
𝑥2𝑛
𝐼 = ∫ 𝑦𝑑𝑥 ≈
𝑥0
h
y2n
x2n
ℎ
(𝑦 + 4𝑦1 + 2𝑦2 + ⋯ + 𝑦2𝑛 ) (Fehler ~ℎ4 )
3 0
19
5.
Reihen
5.1
Zahlenreihen und Potenzreihen
5.1.1 Zahlenreihen
∞
𝑚→∞
𝑠 = ∑ 𝑎𝑛 ←
𝑚
𝑠𝑚 = ∑ 𝑎𝑛
𝑛=1
𝑛=1
Bsp. Geometrische Reihe:
𝑎𝑛 = 𝑞 𝑛 , 𝑠𝑚 = 1 + 𝑞 + ⋯ + 𝑞 𝑚 =
Konvergenz:


1 − 𝑞 𝑚+1 𝑚→∞
1
(|𝑞| < 1)
→
𝑠=
1−𝑞
1−𝑞
𝑛→∞
1
notwendig: 𝑎𝑛 → 0 (nicht hinreichend, z.B. ∑ 𝑛 divergent!)
hinreichend (𝑛 > 𝑛0 ):
𝑎𝑛+1

|



𝑛
𝑎𝑛
| ≤ 𝑞 < 1 (Quotienten-Kriterium)
√|𝑎𝑛 | ≤ 𝑞 < 1 (Wurzel-Kriterium)
𝑎𝑛 alternierend, |𝑎𝑛 | ↘ 0 (Leibniz-Kriterium)
∞
𝑎𝑛 ≥ 0 ∑∞ 𝑎𝑛 < ∫ 𝑓(𝑥)𝑑𝑥 < ∞
(Integral-Kriterium, allg. konvergente Majorante)
f n   an
z.B. 𝑎𝑛 =
1
1
𝛼 > 1:Konvergenz
↷ 𝑓(𝑥) = 𝛼 ⟶
𝛼
𝛼 ≤ 1:Divergenz
𝑛
𝑥
Berechnung: evtl. Funktionswerte von Taylor-/Fourier-Reihen, im allg. numerisch
5.1.2 Potenzreihen
∞
𝑓(𝑥) = ∑ ⏟
𝑎𝑛 (𝑥 − 𝑥0 )𝑛
𝑛=0
Vergleich:
Konvergenz:
𝑓𝑛 (𝑥)
𝑓 (𝑛) (𝑥0 )
Taylor:
geg. 𝑓(𝑥) → 𝑎𝑛 =
𝑛!
Potenz-Reihe: geg. 𝑎𝑛 → 𝑓(𝑥)
𝑎
1
In |𝑥 − 𝑥0 | < 𝑟 = lim |𝑎 𝑛 | =
gleichmäßig, sogar gliedweise
𝑛
|
𝑛→∞
𝑛+1
lim √|𝑎𝑛
differenzier- und integrierbar; 𝑥 − 𝑥0 = ±𝑟 →Sonderuntersuchung
Berechnung: Bekannte Reihen differenzieren, integrieren, multiplizieren, dividieren;
unbestimmte Ansätze benutzen
20
Fourier-Reihen zu 𝒚 = 𝒇(𝒙) mit Periode 𝑻 = 𝟐𝒑
5.2
Ansatz:
∞
𝑎0
𝑛𝜋
𝑛𝜋
reell: 𝑓(𝑥) =
+ ∑ [𝑎𝑛 cos ( 𝑥) + 𝑏𝑛 sin ( 𝑥)]
⏟
2
𝑝
𝑝
𝑓(𝑥)
𝑛=1
∞
komplex: 𝑓(𝑥) = ∑ 𝑐𝑛 𝑒
𝑗
𝑛𝜋
𝑥
𝑝
𝑛=−∞
Koeffizienten:
𝑝
𝑝
1
𝑛𝜋
1
𝑛𝜋
𝑎𝑛 = ∫ 𝑓(𝑥) cos
𝑥 𝑑𝑥 (𝑛 ≥ 0), 𝑏𝑛 = ∫ 𝑓(𝑥) sin
𝑥 𝑑𝑥 (𝑛 ≥ 1)
𝑝
𝑝
𝑝
𝑝
statt
−𝑝
𝑝
∫−𝑝…
−𝑝
auch
2𝑝
∫0 …
𝑓(𝑥) 𝑔𝑒𝑟𝑎𝑑𝑒:
möglich
𝑝
2
𝑎𝑛 = ∫ …
𝑝
𝑏𝑛 = 0
𝑎𝑛 = 0
2
𝑏𝑛 = ∫ …
𝑝
0
𝑓(𝑥) 𝑢𝑛𝑔𝑒𝑟𝑎𝑑𝑒:
𝑝
0
komplex:
𝑝
𝑛𝜋
1
−𝑗 𝑥
𝑐𝑛 =
∫ 𝑓(𝑥)𝑒 𝑝 𝑑𝑥 ⟷ 𝑐𝑛 + 𝑐−𝑛 = 2 Re 𝑐𝑛 = 𝑎𝑛 ; 𝑗(𝑐𝑛 − 𝑐−𝑛 ) = −2 Im 𝑐𝑛 = 𝑏𝑛
2𝑝
−𝑝
1
1
𝑎0
𝑐𝑛 = (𝑎𝑛 − 𝑗𝑏𝑛 ); 𝑐−𝑛 = 𝑐𝑛 = (𝑎𝑛 + 𝑗𝑏𝑛 ); 𝑐0 =
2
2
2
Falls 𝑓(𝑥) stückweise Polynom 𝑃(𝑥), so 𝑎𝑛 , 𝑏𝑛 auch aus Sprunghöhen
(𝑘)
Δ𝑠 = 𝑃 (𝑘) (𝑥𝑠 + 0) − 𝑃 (𝑘) (𝑥𝑠 − 0)
2
1
𝑛𝜋
𝑛𝜋
𝑛𝜋
(0)
(1) 𝑝
(2) 𝑝
𝑎𝑛 =
∑ [−Δ𝑠 sin ( 𝑥𝑠 ) − Δ𝑠
cos ( 𝑥𝑠 ) + Δ𝑠 ( ) sin ( 𝑥𝑠 )
𝑛𝜋
𝑝
𝑛𝜋
𝑝
𝑛𝜋
𝑝
𝑥𝑠 ∈[0,𝑇)
𝑝 3
𝑛𝜋
) cos ( 𝑥𝑠 ) … ]
𝑛𝜋
𝑝
2
1
𝑛𝜋
𝑛𝜋
𝑛𝜋
(0)
(1) 𝑝
(2) 𝑝
𝑏𝑛 =
∑ [Δ𝑠 cos ( 𝑥𝑠 ) − Δ𝑠
sin ( 𝑥𝑠 ) − Δ𝑠 ( ) cos ( 𝑥𝑠 )
𝑛𝜋
𝑝
𝑛𝜋
𝑝
𝑛𝜋
𝑝
(3)
+ Δ𝑠 (
𝑥𝑠 ∈[0,𝑇)
𝑝 3
𝑛𝜋
) sin ( 𝑥𝑠 ) … ]
𝑛𝜋
𝑝
Tricks: 𝑓(𝑥) verschieben, Differenzieren, Integrieren und Tabellen nutzen
(3)
+ Δ𝑠 (
1
1
1
Koeffizientenordnung:
~𝑛
~ 𝑛2
~ 𝑛3
Amplitudenspektrum aus 𝑎𝑛 cos 𝜔𝑛 𝑥 + 𝑏𝑛 sin 𝜔𝑛 𝑥 = 𝐴𝑛 cos(𝜔𝑛 𝑥 − 𝜑𝑛 )
𝑏
Amplitude 𝐴𝑛 = √𝑎𝑛2 + 𝑏𝑛2 , Phase 𝜑𝑛 : tan 𝜑𝑛 = 𝑎𝑛
𝑛
21
An
ϕn b n
an
𝑝
∞
𝑎0 2
1
( ) + ∑(𝑎𝑛2 + 𝑏𝑛2 ) = ∫|𝑓(𝑥)|2 𝑑𝑥
2
𝑝
𝑛=1
5.3
−𝑝
Tabelle Fourier-Reihen
Fourier-Reihe (eventuell Substitution 𝜔𝑡 = 𝑚𝑥 + 𝑛 nutzen)
Nr. Zeitfunktionen
Rechteckkurve
f(ωt)
A
1
-π
4𝐴
1
1
[sin(𝜔𝑡) + sin(3𝜔𝑡) + sin(5𝜔𝑡) + ⋯ ]
𝜋
3
5
𝐴1 + 𝐴2 2(𝐴1 − 𝐴2 )
+
⋅ [Klammer von oben])
(𝑎𝑙𝑙𝑔. 𝑓(𝜔𝑡) =
2
𝜋
⟶ 𝐴1 = 𝐴, 𝐴2 = −𝐴
𝑓(𝜔𝑡) =
(A1)
π 2π 3π
ωt
(A2)
Dreieckkurven
f(ωt)
2
8𝐴
𝜔𝑡
1
3𝜔𝑡
1
5𝜔𝑡
(
)
+
cos
(
)
+
cos
(
)+ ⋯]
[cos
𝜋2
2
9
2
25
2
Vgl. 𝜔𝑡2 ↔ 𝜔𝑡3 − 𝜋
𝑓(𝜔𝑡) =
A
-π
π
2π 3π
ωt
f(ωt)
A
3
-π
π 2π 3π
ωt
𝑓(𝜔𝑡) =
8𝐴
𝜔𝑡
1
3𝜔𝑡
1
5𝜔𝑡
) + sin (
) − +⋯]
[sin ( ) − sin (
2
𝜋
2
9
2
25
2
Vgl. 2. um A heben, 2A durch A ersetzen (𝐴3. ↔ 𝐴2. ), 𝜔𝑡3. ↔
𝜔𝑡2.
2
f(ωt)
A
4
-π
π 2π 3π
ωt
𝑓(𝜔𝑡) =
𝐴 4𝐴
𝜔𝑡
1
1
+ 2 [cos ( ) + cos(3𝜔𝑡) + cos(5𝜔𝑡) + ⋯ ]
2 𝜋
2
9
25
𝐴4.
1 𝑑 −𝜋
→ ⋅ …→
𝜔 𝑑𝑡
→ 𝐴1.
1.
Trapezkurve
f(ωt)
A
5
-π
𝑓(𝜔𝑡) =
a
π
2π 3π ωt
4𝐴
1
[sin 𝑎 sin(𝜔𝑡) + sin(3𝑎) sin(3𝜔𝑡)
𝑎𝜋
9
1
+ sin(5𝑎) sin(5𝜔𝑡) + ⋯ ]
25
22
Parabelbögen
𝐴
(𝜔𝑡 − 𝜋)2
𝜋2
6
f(ωt)
A
-π
𝐴 4𝐴
1
1
+ 2 [cos(𝜔𝑡) + cos(2𝜔𝑡) + cos(3𝜔𝑡) + ⋯ ]
3 𝜋
4
9
1 𝑑
2𝐴6. 𝐴7.
→ ⋅
mit 2 →
𝜔 𝑑𝑡
𝜋
𝜋
𝑓(𝜔𝑡) =
ωt
π 2π 3π
Sägezahnkurve
f(ωt)
7
-π
2𝐴
1
1
[sin(𝜔𝑡) + sin(2𝜔𝑡) + sin(3𝜔𝑡) + ⋯ ]
𝜋
2
3
Vgl. 10. 𝐴 ↔ −𝐴
𝑓(𝜔𝑡) = −
A
π 2π
3π
ωt
Sinushalbwellen
f(ωt)
8
-π
𝐴
𝜋
2
2
[1 + sin(𝜔𝑡) − cos(2𝜔𝑡) − cos(4𝜔𝑡) + ⋯ ]
𝜋
2
3
15
𝑑
cos-Signale über 𝑑𝑡 oder ∫ … 𝑑𝑡
𝑓(𝜔𝑡) =
A
π 2π 3π
ωt
Sinushalbwellen
f(ωt)
𝑓(𝜔𝑡) =
A
9
-π
π 2π 3π
ωt
f(ωt)
A
2𝐴
1
1
[sin(𝜔𝑡) + sin(2𝜔𝑡) + sin(3𝜔𝑡) + ⋯ ]
𝜋
2
3
Vgl. 7. 𝐴 ↔ −𝐴
𝑓(𝜔𝑡) =
10
-π
π
3π ωt
2π
𝑓(𝜔𝑡) =
f(ωt)
A
11
-π
2𝐴
2
2
2
[1 − cos(2𝜔𝑡) − cos(4𝜔𝑡) − cos(6𝜔𝑡)
𝜋
3
15
35
− ⋯]
π 2π
3π
ωt
𝐴 𝐴
1
1
+ [sin(𝜔𝑡) − sin(2𝜔𝑡) + sin(3𝜔𝑡) − ⋯ ]
4 𝜋
2
3
2𝐴
1
1
− 2 [cos(𝜔𝑡) + 2 cos(3𝜔𝑡) + 2 cos(5𝜔𝑡)
𝜋
3
5
+ ⋯]
6.
Laplace-Transformation
6.1
ET-Standardsignale

s-Signal (Einheitssprung, auch 𝜎; Heaviside): 𝑠(𝑡) = {
23
0 𝑡<0
1 𝑡>0

𝛿-Signal (Einheitsimpuls, Dirac): 𝛿(𝑡) = lim
1
𝜀→+0 𝜀
[𝑠(𝑡) − 𝑠(𝑡 − 𝜀)]
1
1/ε
1
1
ε

𝜔-Signal (Harmonische Schwingung):
Reell: 𝑓(𝑡) = 𝐴 sin(𝜔𝑡 + 𝜑) = 𝑎 cos 𝜔𝑡 + 𝑏 sin 𝜔𝑡 𝐴 = √𝑎2 + 𝑏 2
A
ϕ
b
tan 𝜑 =
𝑎
𝑏
a
Komplex: 𝑓(𝑡) = 𝐴 ⋅ 𝑒 𝑗(𝜔𝑡+𝜑) = 𝐴𝑒 𝑗𝜔𝑡 𝐴 = 𝐴𝑒 𝑗𝜑

F-Signal (Periodische Schwingung, Fourier): Periode 𝑇 = 2𝑝
2𝜋
2𝜋
𝜔𝑛 = 𝑇 𝑛, Δ𝜔 = 𝜔𝑛+1 − 𝜔𝑛 = 𝑇
∞
𝑎0
Reell: 𝑓(𝑡) =
+ ∑(𝑎𝑛 cos 𝜔𝑛 𝑡 + 𝑏𝑛 sin 𝜔𝑛 𝑡)
2
𝑛=1
∞
Komplex: 𝑓(𝑡) = ∑ 𝑐𝑛 𝑒 𝑗𝜔𝑛𝑡
𝑛=−∞
𝑇
2
𝑐𝑛 =
1
∫ 𝑓(𝑡)𝑒 −𝑗𝜔𝑡 𝑑𝑡 = Komplexe Amplitude zu 𝜔𝑛 -Anteil
𝑇
−
𝑇
2
Fourier-Transformation (komplexes F-Signal für 𝑻 → ∞):
𝑇
2
∞
𝑓(𝑡) = ∑ 𝑒
𝑗𝜔𝑛 𝑡
𝑛=−∞
∞
𝑇→∞
Δ𝜔
1
⋅
∫ 𝑓(𝑡)𝑒 −𝑗𝜔𝑛𝑡 𝑑𝑡 → 𝑓(𝑡) =
∫ 𝑒 𝑗𝜔𝑡
2𝜋
2𝜋
−
𝑇
2
−∞
⏟
∞
∫ 𝑓(𝑡)𝑒 −𝑗𝜔𝑡 𝑑𝑡 𝑑𝜔
⏟
−∞
( 𝐹(𝑗𝜔)=ℱ{𝑓(𝑡)}←𝑐𝑛 )
ℱ −1 {𝐹(𝑗𝜔)}
|𝐹(𝑗𝜔)| ∶ Amplitudenspektrum
F-Transformation: 𝐹(𝑗𝜔) = {
arg 𝐹(𝑗𝜔) ∶ Phasenspektrum
F-Cosinus-Transformation:
∞
∞
2
2
𝐹𝑐 (𝜔) = √ ∫ 𝑓(𝑡) cos 𝜔𝑡 𝑑𝑡 𝑓(𝑡) = √ ∫ 𝐹𝑐 (𝜔) cos 𝜔𝑡 𝑑𝜔 (𝑡 > 0)
𝜋
𝜋
0
0
F-Sinus-Transformation:
∞
∞
2
2
𝐹𝑠 (𝜔) = √ ∫ 𝑓(𝑡) sin 𝜔𝑡 𝑑𝑡 𝑓(𝑡) = √ ∫ 𝐹𝑠 (𝜔) sin 𝜔𝑡 𝑑𝜔 (𝑡 > 0)
𝜋
𝜋
0
0
24
6.2
Abbildungsgesetze
𝓛{𝒇(𝒕)} = 𝑭(𝒑)
der
Laplace-Transformation
Additionssatz:
ℒ{𝑎1 𝑓1 (𝑡) + 𝑎2 𝑓2 (𝑡)} = 𝑎1 ℒ{𝑓1 (𝑡)} + 𝑎2 ℒ{𝑓2 (𝑡)}
Verschiebungssatz:
ℒ{𝑓(𝑡 − 𝑎)} = 𝑒 −𝑎𝑝 ℒ{𝑓(𝑡)} = 𝑒 −𝑎𝑝 𝐹(𝑝) (𝑡 ≥ 𝑎 > 0)
Ähnlichkeitssatz:
Dämpfungssatz:
1 𝑝
𝐹 ( ) (𝑎 > 0)
𝑎 𝑎
ℒ{𝑒 −𝑎𝑡 𝑓(𝑡)} = 𝐹(𝑝 + 𝑎) (𝑎 ∈ ℂ)
ℒ{𝑓(𝑎𝑡)} =
Multiplikationssatz:
ℒ{𝑡 𝑛 ⋅ 𝑓(𝑡)} = (−1)𝑛 𝐹 (𝑛) (𝑝) (𝑛 = 1,2, … ; 𝐹 (𝑛)
= n-te Ableitung von F)
Divisionssatz:
1
ℒ { 𝑓(𝑡)} = ∫ 𝐹(𝑞)𝑑𝑞 (∫
𝑡
∞
parallel zu reeller Achse)
𝑝
Differentiationssatz:
ℒ{𝑓 ′ (𝑡)} = 𝑝 ⋅ 𝐹(𝑝) − 𝑓(+0)
′
ℒ{𝑓 (𝑛) (𝑡)} = 𝑝𝑛 ⋅ 𝐹(𝑝) − 𝑝𝑛−1 𝑓(+0) − 𝑝𝑛−2 𝑓 (+0) − ⋯
(
)
− 𝑓 𝑛−1 (+0)
Integrationssatz:
𝑡
ℒ {∫ 𝑓(𝜏)𝑑𝜏} =
0
1
𝐹(𝑝)
𝑝
𝑡
Faltungssatz:
ℒ{𝑓1 (𝑡) ∗ 𝑓2 (𝑡)} = 𝐹1 (𝑝) ⋅ 𝐹2 (𝑝) (𝑓1 ∗ 𝑓2 = ∫ 𝑓1 (𝜏) ⋅ 𝑓2 (𝑡 − 𝜏)𝑑𝜏)
0
Transformationsformel:
𝑇
1
ℒ{𝑓(𝑡)} =
∫ 𝑒−𝑝𝑡 𝑓(𝑡)𝑑𝑡 (𝑇:Periode von 𝑓(𝑡))
1 − 𝑒−𝑝𝑇
0
Anfangswertsatz:
𝑓(+0) = lim 𝑝 ⋅ 𝐹(𝑝) (falls 𝑓(+0) ∈ 𝑥; für reelle 𝑝)
Endwertsatz:
𝑓(+∞) = lim 𝑝 ⋅ 𝐹(𝑝) (falls 𝑓(+∞) ∈ 𝑥; d.h. Re 𝑝𝑘 < 0, für reelle 𝑝)
Residuenmethode:
𝑛→∞
𝑛→0
𝑓(𝑡) = ∑
𝑘
1
lim [(𝑝 − 𝑝𝑘 )𝑚𝑘 𝐹(𝑝)𝑒 𝑝𝑡 ](𝑚𝑘 −1)
(𝑚𝑘 − 1)! 𝑝→𝑝𝑘
𝑝𝑘 : Pole mk-ter Ordnung von 𝐹(𝑝), Ableitung nach p
𝐹(𝑝)-Anteile ~𝑒 −𝑎𝑝 ↷ 𝑓(𝑡)-Anteile ab 𝑡 ≥ 𝑎 > 0
Grundformel:
∞
ℒ{𝑓(𝑡)} = 𝐹(𝑝) = ∫ 𝑓(𝑡)𝑒−𝑝𝑡 𝑑𝑡
0
In allen Formeln für 𝑓(𝑡) ⋅ 𝑠(𝑡) kurz 𝑓(𝑡)!
25
6.3
Stationäres Übertragungsverhalten
𝑮(𝒑) ⋅ 𝑿𝒆 (𝒑) (𝐑𝐞 𝒑𝒌 < 𝟎)
von
𝑥𝑒 (𝑡)
𝑥𝑎,𝑠𝑡 (𝑡) (allgemein: 𝑥𝑎 (𝑡) = 𝑔(𝑡) ∗ 𝑥𝑒 (𝑡))
𝛿(𝑡)
0; 𝑥𝑎 (𝑡) = 𝑔(𝑡) = ℎ′ (𝑡)
𝑠(𝑡)
𝑡
𝑿𝒂 (𝒑) =
𝐺(0); 𝑥𝑎 (𝑡) = ℎ(𝑡) = ∫ 𝑔(𝜏)𝑑𝜏
0
𝑒
𝑗𝜔𝑡
𝑗𝜔𝑡
𝐺(𝑗𝜔)𝑒
𝐺(𝑗𝜔): Frequenzgang
|𝐺(𝑗𝜔)|: Amplitudengang
arg 𝐺(𝑗𝜔): Phasengang
∞
𝑎0
+ ∑(𝑎𝑛 cos 𝜔𝑛 𝑡 + 𝑏𝑛 sin 𝜔𝑛 𝑡)
2
𝑛=1
2𝜋
(𝜔𝑛 =
⋅ 𝑛, 2𝑝 = 𝑇:Periode)
2𝑝
6.4
∞
𝑎0
𝐺(0) + ∑[{𝑎𝑛 Re 𝐺(𝑗𝜔𝑛 ) + 𝑏𝑛 Im 𝐺(𝑗𝜔𝑛 )} cos 𝜔𝑛 𝑡
2
𝑛=1
+ {−𝑎𝑛 Im 𝐺(𝑗𝜔𝑛 ) + 𝑏𝑛 Re 𝐺(𝑗𝜔𝑛 )} sin 𝜔𝑛 𝑡]
Korrespondenztabelle zur Laplace-Transformation
Nr. 𝐹(𝑝) = ℒ{𝑓(𝑡)}
1 1
𝑓(𝑡) = ℒ −1 {𝐹(𝑝)} (statt p auch s gebräuchlich)
𝛿(𝑡)
2
1
𝑝
𝑠(𝑡) (Re 𝑝 > 0)
3
1
𝑝2
𝑡 (Re 𝑝 > 0)
4
1
𝑝𝑛
𝑡 𝑛−1
(Re 𝑝 > 0)
(𝑛 − 1)!
5
1
𝑝−𝑎
𝑒 𝑎𝑡 (Re 𝑝 > Re 𝑎)
6
1
𝑝(𝑝 − 𝑎)
1 𝑎𝑡
(𝑒 − 1)
𝑎
1
− 𝑎)
𝑝2 (𝑝
1 𝑎𝑡
(𝑒 − 𝑎𝑡 − 1)
𝑎2
8
1
𝑝(𝑝 − 𝑎)2
1
[1 + (𝑎𝑡 − 1)𝑒 𝑎𝑡 ]
𝑎2
9
1
(𝑝 − 𝑎)(𝑝 − 𝑏)
1
[𝑒 𝑎𝑡 − 𝑒 𝑏𝑡 ]
𝑎−𝑏
10
1
𝑝(𝑝 − 𝑎)(𝑝 − 𝑏)
1
𝑏𝑒 𝑎𝑡 − 𝑎𝑒 𝑏𝑡
[1 +
]
𝑎𝑏
𝑎−𝑏
11
𝑝
(𝑝 − 𝑎)2
(1 + 𝑎𝑡)𝑒 𝑎𝑡
7
26
Nr. 𝐹(𝑝) = ℒ{𝑓(𝑡)}
𝑝
12
(𝑝 − 𝑎)3
𝑝2
(𝑝 − 𝑎)3
𝑝
14
(𝑝 − 𝑎)(𝑝 − 𝑏)
13
15
16
17
18
19
20
1
(𝑝 − 𝑎)(𝑝 − 𝑏)(𝑝 − 𝑐)
𝑝
(𝑝 − 𝑎)(𝑝 − 𝑏)(𝑝 − 𝑐)
𝑎
2
𝑝 − 𝑎2
𝑝
𝑝2 − 𝑎2
𝜔
2
𝑝 + 𝜔2
𝜔2
𝑝(𝑝2 + 𝜔 2 )
𝜔2
𝑝2 (𝑝2 + 𝜔 2 )
𝑝
22
𝑝2 + 𝜔 2
1
(𝑝 + 𝑎)(𝑝2 + 𝜔 2 )
1
+
𝜔12 )(𝑝2
𝑎2 𝑡 2 𝑎𝑡
)𝑒
2
1
[𝑎𝑒 𝑎𝑡 − 𝑏𝑒 𝑏𝑡 ]
𝑎−𝑏
1
[(𝑏 − 𝑐)𝑒 𝑎𝑡 + (𝑐 − 𝑎)𝑒 𝑏𝑡 + (𝑎 − 𝑏)𝑒 𝑐𝑡 ]
(𝑎 − 𝑏)(𝑎 − 𝑐)(𝑏 − 𝑐)
1
[𝑎(𝑏 − 𝑐)𝑒 𝑎𝑡 + 𝑏(𝑐 − 𝑎)𝑒 𝑏𝑡 + 𝑐(𝑎 − 𝑏)𝑒 𝑐𝑡 ]
(𝑎 − 𝑏)(𝑎 − 𝑐)(𝑏 − 𝑐)
1 𝑎𝑡
(𝑒 − 𝑒 −𝑎𝑡 ) = sinh 𝑎𝑡
2
1 𝑎𝑡
(𝑒 + 𝑒 −𝑎𝑡 ) = cosh 𝑎𝑡
2
sin 𝜔𝑡
𝜔𝑡
2
1
sin 𝜔𝑡
𝜔
cos 𝜔𝑡
𝜔3
(𝑝2 + 𝜔 2 )2
𝜔𝑝
24
2
(𝑝 + 𝜔 2 )2
(𝑝2
(1 + 2𝑎𝑡 +
𝑡−
23
26
1
(𝑡 + 𝑎𝑡 2 ) 𝑒 𝑎𝑡
2
1 − cos 𝜔𝑡 = 2 sin2
21
25
𝑓(𝑡) = ℒ −1 {𝐹(𝑝)} (statt p auch s gebräuchlich)
+ 𝜔22 )
1
(sin 𝜔𝑡 − 𝜔𝑡 ⋅ cos 𝜔𝑡)
2
𝑡
sin 𝜔𝑡
2
1
𝑎
[𝑒 −𝑎𝑡 − cos 𝜔𝑡 + sin 𝜔𝑡]
2
2
𝑎 +𝜔
𝜔
𝑒 −𝑎𝑡
1
= 2
+
sin(𝜔𝑡 + 𝜑)
2
2
𝑎 +𝜔
𝜔√𝑎 + 𝜔 2
𝜔
(mit tan 𝜑 = )
𝑎
1
[𝜔1 sin 𝜔2 𝑡 − 𝜔2 sin 𝜔1 𝑡]
𝜔1 𝜔2 (𝜔12 − 𝜔22 )
27
𝜔
(𝑝 + 𝛿)2 + 𝜔 2
𝑒 −𝛿𝑡 sin 𝜔𝑡
28
𝑝+𝛿
(𝑝 + 𝛿)2 + 𝜔 2
𝑒 −𝛿𝑡 cos 𝜔𝑡
29
1
1
𝛿−𝑎
sin 𝜔𝑡)]
[𝑒 −𝑎𝑡 − 𝑒 −𝛿𝑡 (cos 𝜔𝑡 +
(𝑝 + 𝑎)[(𝑝 + 𝛿)2 + 𝜔 2 ] (𝛿 − 𝑎)2 + 𝜔 2
𝜔
27
7.
Differentialgleichungen
7.1
DGL-Lösungsmethoden
7.1.1 Trennung der Variablen
Typ: 𝑦 ′ =
𝑑𝑦
𝑑𝑦
= 𝑔(𝑥) ⋅ ℎ(𝑦) ⟶
= 𝑔(𝑥)𝑑𝑥 |∫
𝑑𝑥
ℎ(𝑦)
⟶ implizite Lösung
7.1.2 Allgemeine Lineare DGL 1. Ordnung
𝑇𝑦𝑝: 𝑦 ′ + 𝑎0 (𝑥)𝑦 = 𝑆(𝑥)
homogene DGL (𝑆(𝑥) = 0):
𝑦 = 𝑦ℎ = 𝐶 ⋅ 𝑒 − ∫ 𝑎0 (𝑥)𝑑𝑥
y über I.
inhomogene DGL (𝑆(𝑥) ≠ 0): 𝑦 = 𝑦 + 𝑦 = [∫ 𝑆(𝑥)𝑒 ∫ 𝑎0 (𝑥)𝑑𝑥 𝑑𝑥 + 𝐶] ⋅ 𝑒 − ∫ 𝑎0 (𝑥)𝑑𝑥
𝑝
ℎ
über 𝐶 = 𝐶(𝑥): Variation der Konstanten
7.1.3 Lineare DGL mit konstanten Koeffizienten
𝑛
Typ: ∑ 𝑎𝑘 𝑦 (𝑘) = 𝑆(𝑥) (alternativ zu a,b):Laplace-Transformation)
𝑘=0
a)
homogene DGL (𝑆(𝑥) = 0): Ansatz 𝑦 = 𝑒 𝜆𝑥 in DGL → charakteristisches Polynom
𝑛
𝑚
𝑘
𝑃𝑛 (𝜆) = ∑ 𝑎𝑘 𝜆 = 𝑎𝑛 ⋅ ∏(𝜆 − 𝜆𝑘
𝑛
𝑘=0
𝑚
)𝑟𝑘
= 0 (∑ 𝑟𝑘 = 𝑛; 𝜆𝑘 ∈ ℂ)
𝑘=1
𝑘=1
𝑦 = ∑ 𝑐𝑘 𝑦𝑘 (𝑥) ; {𝑦𝑘 (𝑥)} = {𝑒 𝜆𝑘 𝑥 ⋅ 𝑥 𝑖 ;
𝑘=1
b)
𝑘 = 1, … , 𝑚
}
𝑖 = 0, … , 𝑟𝑘−1
inhomogene DGL (𝑆(𝑥) ≠ 0): 𝑆(𝑥) = (𝑏0 + 𝑏1 𝑥 + ⋯ + 𝑏𝑚 𝑥 𝑚 )𝑒 𝜆𝑠 𝑥 ; 𝜆𝑠 ∈ ℂ (eventuell
auch reelle Rechnung)
Ansatz: 𝑦𝑝 (𝑥) = (𝐵0 + 𝐵1 𝑥 + ⋯ + 𝐵𝑚 𝑥 𝑚 )𝑒 𝜆𝑠 𝑥 ⋅ 𝑥 𝑟𝜆𝑠 falls 𝜆𝑠 𝑟𝜆𝑠 -fache Nullstelle von
𝑃𝑛 (𝜆)
Beachte: Berechnung der 𝐶𝑘 erst nach allgemeiner Lösung 𝑦 = 𝑦ℎ + 𝑦𝑝
28