Differenzialrechnung_Schuluebung_7i_1314

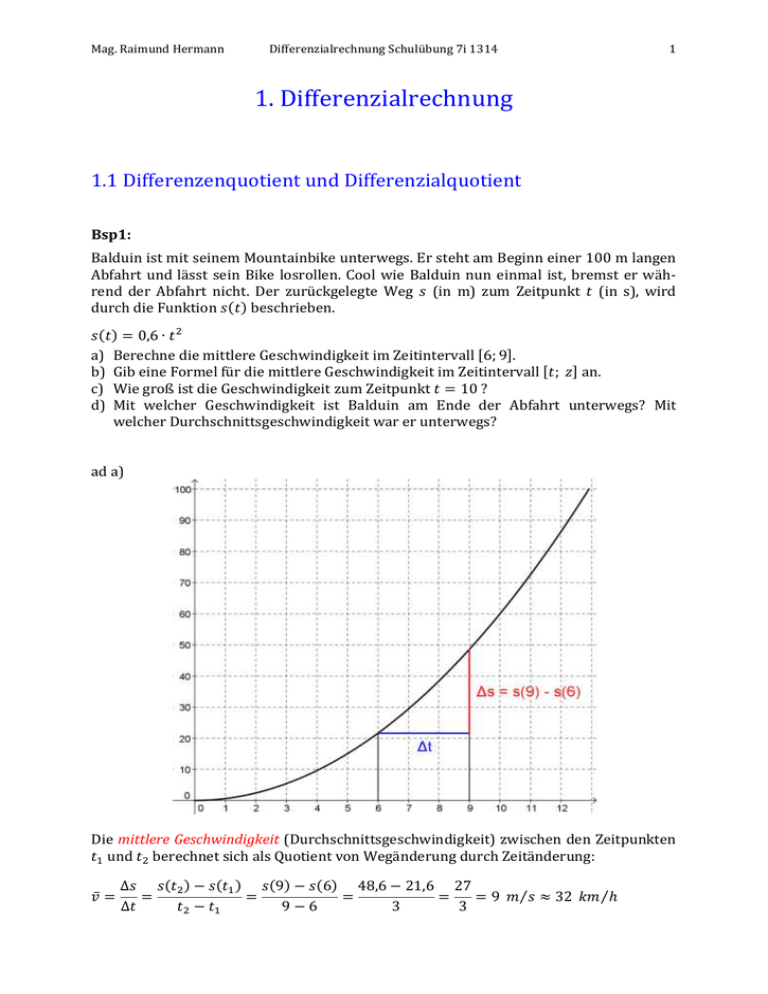
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
1
1. Differenzialrechnung
1.1 Differenzenquotient und Differenzialquotient
Bsp1:
Balduin ist mit seinem Mountainbike unterwegs. Er steht am Beginn einer 100 m langen
Abfahrt und lässt sein Bike losrollen. Cool wie Balduin nun einmal ist, bremst er während der Abfahrt nicht. Der zurückgelegte Weg 𝑠 (in m) zum Zeitpunkt 𝑡 (in s), wird
durch die Funktion 𝑠(𝑡) beschrieben.
𝑠(𝑡) = 0,6 ∙ 𝑡 2
a) Berechne die mittlere Geschwindigkeit im Zeitintervall [6; 9].
b) Gib eine Formel für die mittlere Geschwindigkeit im Zeitintervall [𝑡; 𝑧] an.
c) Wie groß ist die Geschwindigkeit zum Zeitpunkt 𝑡 = 10 ?
d) Mit welcher Geschwindigkeit ist Balduin am Ende der Abfahrt unterwegs? Mit
welcher Durchschnittsgeschwindigkeit war er unterwegs?
ad a)
Die mittlere Geschwindigkeit (Durchschnittsgeschwindigkeit) zwischen den Zeitpunkten
𝑡1 und 𝑡2 berechnet sich als Quotient von Wegänderung durch Zeitänderung:
𝑣̅ =
∆𝑠 𝑠(𝑡2 ) − 𝑠(𝑡1 ) 𝑠(9) − 𝑠(6) 48,6 − 21,6 27
=
=
=
=
= 9 𝑚⁄𝑠 ≈ 32 𝑘𝑚⁄ℎ
∆𝑡
𝑡2 − 𝑡1
9−6
3
3
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
2
ad b)
∆𝑠 𝑠(𝑧) − 𝑠(𝑡) 0,6 ∙ 𝑧 2 − 0,5 ∙ 𝑡 2 0,6 ∙ (𝑧 2 − 𝑡 2 ) 0,6 ∙ (𝑧 − 𝑡) ∙ (𝑧 + 𝑡)
=
=
=
=
∆𝑡
𝑧−𝑡
𝑧−𝑡
𝑧−𝑡
𝑧−𝑡
∆𝑠
𝑣̅ =
= 0,6 ∙ (𝑧 + 𝑡)
∆𝑡
𝑣̅ =
Beispielsweise beträgt die mittlere Geschwindigkeit im Zeitintervall [6; 9]
𝑣̅ = 0,6 ∙ (𝑧 + 𝑡) = 0,6 ∙ (9 + 6) = 9 𝑚⁄𝑠
ad c)
Um die Geschwindigkeit zum Zeitpunkt 𝑡 = 10 zu bestimmen, berechnen wir die Durchschnittsgeschwindigkeit in immer kleiner werdenden Zeitintervallen [𝑡; 𝑧]. D.h. wir
wählen z immer näher bei 𝑡. Die Intervalllänge ∆𝑡 = 𝑧 − 𝑡 geht somit gegen Null.
Zeitintervall
[10; 𝑧]
mittlere Geschwindigkeit
𝑣̅ = 0,6 ∙ (𝑧 + 10)
[10;
[10;
[10;
[10;
[10;
12,6
12,06
12,006
12,0006
12,00006
11]
10,1]
10,01]
10,001]
10,0001]
𝑣(3) = lim 0,6 ∙ (𝑧 + 10) = 0,6 ∙ 20 = 12 𝑚⁄𝑠
𝑧→10
𝑣(𝑡) = lim 0,6 ∙ (𝑧 + 𝑡) = 0,6 ∙ (𝑡 + 𝑡) = 0,6 ∙ 2𝑡 = 1,2 ∙ 𝑡
𝑧→𝑡
Die Funktion 𝑣 ordnet jedem Zeitpunkt 𝑡 die Momentangeschwindigkeit 𝑣(𝑡) zu.
Ein Körper bewegt sich gemäß der Zeit - Ort - Funktion 𝑠(𝑡)
𝑣̅ =
∆𝑠 𝑠(𝑡2 ) − 𝑠(𝑡1 )
=
∆𝑡
𝑡2 − 𝑡1
𝑠(𝑧) − 𝑠(𝑡)
𝑧→𝑡
𝑧−𝑡
𝑣(𝑡) = lim
Mittlere Geschwindigkeit im Zeitintervall [𝑡1 ; 𝑡2 ]
Momentangeschwindigkeit zum Zeitpunkt 𝑡
ad d)
𝑠(𝑡) = 0,6 ∙ 𝑡 2 → 100 = 0,6 ∙ 𝑡 2 → 𝑡 ≈ 12,910 𝑠
𝑣(𝑡) = 1,2 ∙ 𝑡 → 𝑣(12,910) = 1,2 ∙ 12,910 ≈ 15,492 𝑚⁄𝑠 ≈ 56 𝑘𝑚⁄ℎ
𝑣̅ = 0,6 ∙ (𝑧 + 𝑡) = 0,6 ∙ (12,910 + 0) = 0,6 ∙ 12,910 = 7,746 𝑚⁄𝑠 ≈ 28 𝑘𝑚⁄ℎ
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
3
Bsp2:
Ein zylinderförmiges Regenfass hat einen Durchmesser von 84 cm und eine Höhe von
100 cm. Am Boden befindet sich eine Abflussöffnung mit einem Durchmesser von 4 cm.
Die Funktion ℎ beschreibt die Höhe ℎ(𝑡) des Flüssigkeitsspiegels in Abhängigkeit der
Zeit t, wobei Füllhöhe zum Zeitpunkt 𝑡 = 0 gleich 100 cm ist. Die Höhe wird in cm, die
Zeit in Sekunden angegeben.
ℎ(𝑡) = (1 − 0,05 ∙ 𝑡)2
a) Nach welcher Zeit ist das Regenfass leer?
b) Berechne die Änderung der Höhe in den Intervallen [10; 15] und [180; 185].
c) Berechne die mittlere Abnahmegeschwindigkeit der Höhe in den Intervallen
[0; 200], [10; 15] und [180; 185]
d) Gib eine Formel für die mittlere Abnahmegeschwindigkeit der Höhe im Zeitintervall
[𝑡; 𝑧] an.
e) Gib eine Formel für die Abnahmegeschwindigkeit der Höhe zum Zeitpunkt 𝑡 an.
Berechne die Abnahmegeschwindigkeit der Höhe nach 10s, nach 180s und 200s.
ad a)
0 = (10 − 0,05 ∙ 𝑡)2 → 0 = 10 − 0,05 ∙ 𝑡 → 𝑡 = 200
ad b)
∆ℎ = ℎ(15) − ℎ(10) = −4,687
Im Zeitintervall [10; 15] nimmt die Höhe um rund 4,7 cm ab.
∆ℎ = ℎ(185) − ℎ(180) = −0,438
Im Zeitintervall [180; 185] nimmt die Höhe um rund 0,4 cm ab.
ad c)
∆ℎ ℎ(200) − ℎ(0) 0 − 100
=
=
= −0,5
∆𝑡
200 − 0
200
Im Zeitintervall [0; 200] nimmt die Höhe im Mittel um 0,5 𝑐𝑚⁄𝑠 ab.
∆ℎ ℎ(15) − ℎ(10) −4,687
=
=
= −0,937
∆𝑡
15 − 10
5
Im Zeitintervall [10; 15] nimmt die Höhe im Mittel um 0,9 𝑐𝑚⁄𝑠 ab.
∆ℎ ℎ(200) − ℎ(0) −0,438
=
=
= −0,088
∆𝑡
185 − 180
5
Im Zeitintervall [180; 180] nimmt die Höhe im Mittel um 0,09 𝑐𝑚⁄𝑠 ab.
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
4
ad d)
∆ℎ ℎ(𝑧) − ℎ(𝑡) (10 − 0,05 ∙ 𝑧)2 − (10 − 0,05 ∙ 𝑡)2
=
=
∆𝑡
𝑧−𝑡
𝑧−𝑡
∆ℎ 100 − 𝑧 + 0,0025 ∙ 𝑧 2 − 100 + 𝑡 − 0,0025 ∙ 𝑡 2 0,0025 ∙ (𝑧 2 − 𝑡 2 ) − 𝑧 + 𝑡
=
=
∆𝑡
𝑧−𝑡
𝑧−𝑡
∆ℎ 0,0025 ∙ (𝑧 − 𝑡) ∙ (𝑧 + 𝑡) − (𝑧 − 𝑡) (𝑧 − 𝑡) ∙ (0,0025 ∙ (𝑧 + 𝑡) − 1)
=
=
∆𝑡
𝑧−𝑡
𝑧−𝑡
∆ℎ
= 0,0025 ∙ (𝑧 + 𝑡) − 1
∆𝑡
ad e)
ℎ(𝑧) − ℎ(𝑡)
= lim 0,0025 ∙ (𝑧 + 𝑡) − 1 = 0,0025 ∙ (𝑡 + 𝑡) − 1
𝑧→𝑡
𝑧→𝑡
𝑧−𝑡
𝑣(𝑡) = 0,0025 ∙ 2 ∙ 𝑡 − 1 = 0,005 ∙ 𝑡 − 1
𝑣(𝑡) = lim
𝑣(10) = 0,005 ∙ 10 − 1 = −0,95
Nach 10s ändert sich die Höhe mit einer Geschwindigkeit von −0,95 𝑐𝑚⁄𝑠
𝑣(180) = 0,005 ∙ 180 − 1 = −0,1
Nach 10s ändert sich die Höhe mit einer Geschwindigkeit von −0,1 𝑐𝑚⁄𝑠
𝑣(200) = 0,005 ∙ 200 − 1 = 0
Nach 10s ändert sich die Höhe mit einer Geschwindigkeit von 0 𝑐𝑚⁄𝑠
Beachte:
In dieser Aufgabe beschreibt die Funktion 𝑣 mit welcher Geschwindigkeit sich die Höhe
ändert.
Die Funktion 𝑣 wird auch mit ℎ′ bezeichnet, also ℎ′ (𝑡) = 𝑣(𝑡) = 0,005 ∙ 𝑡 − 1
Es sei 𝑓: 𝐴 → ℝ: 𝑥 ↦ 𝑓(𝑥) eine reelle Funktion und [𝑎; 𝑏] ⊆ 𝐴
∆𝑦 𝑓(𝑏) − 𝑓(𝑎)
=
∆𝑥
𝑏−𝑎
𝑓(𝑧) − 𝑓(𝑥)
𝑧→𝑥
𝑧−𝑥
𝑓 ′ (𝑥) = lim
Differenzenquotient, mittlere Änderungsrate von 𝑓 in [𝑎; 𝑏]
Differenzialquotient von 𝑓 an der Stelle 𝑥
Änderungsrate von 𝑓 an der Stelle 𝑥
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
5
Bsp3:
Wird ein Stein ins Wasser geworfen, so geht vom Aufprallpunkt eine kreisförmige Welle
aus. Die Wellenfront ist ein Kreis mit zunehmenden Radius 𝑟 (in m). Ein derartiger Kreis
hat den Flächeninhalt 𝐴(𝑟).
a) Berechne die Zunahme des Flächeninhalts in den Intervallen [1; 2] und [2; 3].
b) Berechne die mittlere Änderungsrate des Flächeninhalts in den Intervallen [1; 2] und
[2; 3]
c) Gib eine Formel für die mittlere Änderungsrate des Flächeninhalts im Intervall [𝑟; 𝑧]
an.
d) Gib eine Formel für die Änderungsrate des Flächeninhalts an.
Berechne die Änderungsrate des Flächeninhalts für 𝑟 = 1, 𝑟 = 2 und 𝑟 = 3 .
Bsp4: Das Tangentenproblem
Die Gerade 𝑠 durch die Punkte 𝑃 und 𝑄 ist eine Sekante, da sie die Funktion 𝑓 in mehr als
einem Punkt schneidet.
Die Sekantensteigung berechnet sich als
∆𝑦 𝑓(𝑏) − 𝑓(𝑎)
=
∆𝑥
𝑏−𝑎
Der Differenzenquotient (die mittlere Änderungsrate) einer Funktion 𝑓 in [𝑎; 𝑏] ist
gleich der Steigung der Sekante durch die Punkte 𝑃(𝑎|𝑓(𝑎)) und 𝑄(𝑏|𝑓(𝑏))
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
Die mittlere Änderungsrate im Intervall [𝑥; 𝑧] ist gleich
6
∆𝑦 𝑓(𝑧) − 𝑓(𝑥)
=
∆𝑥
𝑧−𝑥
Rückt der Punkt Q immer näher zum Punkt 𝑃, so fallen schließlich die Punkte 𝑃 und 𝑄
zusammen und die Differenz ∆𝑥 = 𝑧 − 𝑥 wird unendlich klein. Aus der Sekante durch die
Punkte 𝑃 und 𝑄 wird eine Tangente durch den Punkt 𝑃. Eine Tangente ist eine Gerade,
welche die Funktion nur in einem Punkt berührt.
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
7
Die Steigung der Tangente im Punkt P lässt sich Grenzwert der Sekantensteigung berechnen:
𝑓 ′ (𝑥) =
𝑑𝑦
𝑓(𝑧) − 𝑓(𝑥)
= lim
𝑑𝑥 𝑧→𝑥
𝑧−𝑥
Sei 𝑓 eine reelle Funktion und 𝑓 ′ (𝑥) ihr Differentialquotient an der Stelle 𝑥.
Der Differenzialquotient (die Änderungsrate) einer Funktion 𝑓 an der Stelle 𝑥 ist gleich
der Steigung der Tangente durch die Punkte 𝑃(𝑥|𝑓(𝑥)).
Die Steigung einer Funktion 𝑓 an der Stelle 𝑥 ist gleich der Steigung der Tangente im
Punkt 𝑃(𝑥|𝑓(𝑥)).
𝑓 ′ (𝑥) =
𝑑𝑦
𝑓(𝑧) − 𝑓(𝑥)
= lim
𝑑𝑥 𝑧→𝑥
𝑧−𝑥
Alternative Schreibweise:
∆𝑦 𝑓(𝑧) − 𝑓(𝑥) 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥)
=
=
∆𝑥
𝑧−𝑥
∆𝑥
𝑓 ′ (𝑥) =
𝑑𝑦
𝑓(𝑧) − 𝑓(𝑥)
𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥)
= lim
= lim
∆𝑥→0
𝑑𝑥 𝑧→𝑥
𝑧−𝑥
∆𝑥
Differenzenquotient
Differentialquotient
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
1.2 Polynomfunktionen
Eine reelle Funktion 𝑓 der Form 𝑓(𝑥) = 𝑎𝑛 ∙ 𝑥 𝑛 + 𝑎𝑛−1 ∙ 𝑥 𝑛−1 + … + 𝑎1 ∙ 𝑥 + 𝑎0
mit 𝑛 ∈ ℕ, 𝑎𝑛 , 𝑎𝑛−1 , … , 𝑎0 ∈ ℝ und 𝑎𝑛 ≠ 0 heißt Polynomfunktion vom Grad 𝑛.
Beispiele:
𝑓(𝑥) = 3 ∙ 𝑥 2 − 2𝑥 + 3
Polynom vom Grad 2
𝑓(𝑥) = −2 ∙ 𝑥 3 + 3 ∙ 𝑥 2 + 4 ∙ 𝑥 − 5
Polynom vom Grad 3
𝑓(𝑥) = −𝑥 4 + 4 ∙ 𝑥 3 − 5 ∙ 𝑥
Polynom vom Grad 4
Die Funktion 𝑓 ′ : 𝑥 ↦ 𝑓 ′ (𝑥) heißt Ableitungsfunktion von 𝑓 oder Ableitung von 𝑓.
Das Berechnen der Ableitungsfunktion heißt Ableiten oder Differenzieren.
Bsp1:
1
𝑓(𝑥) = − ∙ 𝑥 2 + 2 ∙ 𝑥 + 5
4
Berechne die Ableitungsfunktion. Zeichne die Graphen von 𝑓 und 𝑓 ′ .
1
1
− 4 ∙ 𝑧2 + 2 ∙ 𝑧 + 5 + 4 ∙ 𝑥2 − 2 ∙ 𝑥 − 5
𝑑𝑦
𝑓(𝑧)
−
𝑓(𝑥)
𝑓 ′ (𝑥) =
= lim
= lim
𝑧→𝑥
𝑑𝑥 𝑧→𝑥
𝑧−𝑥
𝑧−𝑥
𝑓 ′ (𝑥) = lim
1
− 4 ∙ (𝑧 2 − 𝑥 2 ) + 2 ∙ (𝑧 − 𝑥)
𝑧−𝑥
𝑧→𝑥
𝑓 ′ (𝑥) = lim −
𝑧→𝑥
= lim
𝑧→𝑥
1
− 4 ∙ (𝑧 − 𝑥) ∙ (𝑧 + 𝑥) + 2 ∙ (𝑧 − 𝑥)
𝑧−𝑥
1
1
1
∙ (𝑧 + 𝑥) + 2 = − ∙ (𝑥 + 𝑥) + 2 = − ∙ 2 ∙ 𝑥 + 2
4
4
4
1
𝑓 ′ (𝑥) = − ∙ 𝑥 + 2
2
8
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
Bsp2: Ableitungsregeln
𝑓(𝑥) = 𝑐 (𝑐 ∈ ℝ)
𝑓 ′ (𝑥) = 0
→
Ableitung einer Konstanten
𝑓(𝑧) − 𝑓(𝑥)
𝑐−𝑐
0
= lim
= lim
= lim 0 = 0
𝑧→𝑥
𝑧→𝑥 𝑧 − 𝑥
𝑧→𝑥 𝑧 − 𝑥
𝑧→𝑥
𝑧−𝑥
𝑓 ′ (𝑥) = lim
𝑓(𝑥) = 𝑐 ∙ 𝑔(𝑥) (𝑐 ∈ ℝ)
→
𝑓 ′ (𝑥) = 𝑐 ∙ 𝑔′ (𝑥)
Regel vom konstanten Faktor
𝑓(𝑧) − 𝑓(𝑥)
𝑐 ∙ 𝑔(𝑧) − 𝑐 ∙ 𝑔(𝑥)
𝑔(𝑧) − 𝑔(𝑥)
= lim
= lim 𝑐 ∙
= 𝑐 ∙ 𝑔′ (𝑥)
𝑧→𝑥
𝑧→𝑥
𝑧→𝑥
𝑧−𝑥
𝑧−𝑥
𝑧−𝑥
𝑓 ′ (𝑥) = lim
𝑓(𝑥) = 𝑢(𝑥) + 𝑣(𝑥)
→
𝑓 ′ (𝑥) = 𝑢′ (𝑥) + 𝑣 ′ (𝑥)
Summenregel
𝑢(𝑧) + 𝑣(𝑧) − (𝑢(𝑥) + 𝑣(𝑥))
𝑓(𝑧) − 𝑓(𝑥)
= lim
𝑧→𝑥
𝑧→𝑥
𝑧−𝑥
𝑧−𝑥
𝑢(𝑧) + 𝑣(𝑧) 𝑢(𝑥) + 𝑣(𝑥)
𝑓 ′ (𝑥) = lim
−
= 𝑢′ (𝑥) + 𝑣 ′ (𝑥)
𝑧→𝑥
𝑧−𝑥
𝑧−𝑥
𝑓 ′ (𝑥) = lim
𝑓(𝑥) = 𝑥 𝑛 (𝑛 ∈ ℝ)
→
𝑓 ′ (𝑥) = 𝑛 ∙ 𝑥 𝑛−1
Potenzregel
9
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
Bsp3:
Berechne die Ableitung
1) 𝑓(𝑥) = 2𝑥 ∙ (2𝑥 − 4)
1 4 1 3 7 2
𝑥 + 𝑥 − 𝑥 − 4𝑥 + 12
16
4
4
4
𝑥
3
𝑓(𝑥) =
− 𝑥 3 + 2𝑥
2 2
𝑥 3 − 2𝑥 + 4
𝑦(𝑥) =
5
1
1
𝑦(𝑥) = 𝑥 3 + 𝑥 2 − 4𝑥 − 5
6
4
𝑦(𝑥) = (2𝑥 + 4) ∙ (2𝑥 − 4)
2) 𝑓(𝑥) =
3)
4)
5)
6)
Bsp4:
1
∙ (𝑥 3 − 3𝑥 2 − 24𝑥)
8
Bestimme die Nullstellen.
Ermittle die Monotoniebereiche und lokalen Extremstellen.
Ermittle die Krümmungsbereiche und Wendestellen.
Ist die Funktion achsensymmetrisch oder punktsymmetrisch?
Wie verhält sich die Funktion für 𝑥 → ±∞ ?
𝑓(𝑥) =
a)
b)
c)
d)
e)
ad a)
1
∙ (𝑥 3 − 3𝑥 2 − 24𝑥) = 0 → 𝑥 3 − 3𝑥 2 − 24𝑥 = 0
8
𝑥 ∙ (𝑥 2 − 3𝑥 − 24) = 0 → 𝑥1 = 0; 𝑥2 = −3,623; 𝑥3 = 6,623
𝑓(𝑥) = 0 →
𝑁1 (0|0), 𝑁2 (−3,623|0), 𝑁3 (6,623|0)
10
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
11
ad b)
In den Intervallen ]−∞; 2[ und ]4; ∞[ ist
die Funktion 𝑓 streng monoton steigend.
In diesen Bereichen ist 𝑓 ′ (𝑥) > 0
Im Intervall ]−2; 4[ ist die Funktion 𝑓
streng monoton fallend.
In diesem Bereichen ist 𝑓 ′ (𝑥) < 0
Bei den lokalen Extremstellen 𝑥 = −2 und
𝑥 = −2 ändert sich das Monotonieverhalten von 𝑓.
An diesen Stellen ist 𝑓 ′ (𝑥) = 0
Bei den Punkten H (lokales Maximum)
und T (lokales Minimum) verläuft die
Tangente waagrecht und hat somit eine
Steigung gleich Null.
1
∙ (𝑥 3 − 3𝑥 2 − 24𝑥)
8
1
𝑓 ′ (𝑥) = ∙ (3𝑥 2 − 6𝑥 − 24)
8
1
𝑓 ′ (𝑥) = 0 →
∙ (3𝑥 2 − 6𝑥 − 24) = 0 → 3𝑥 2 − 6𝑥 − 24 = 0 → 𝑥 2 − 2𝑥 − 8 = 0
8
𝑓(𝑥) =
𝑥1 = −2
𝑓(−2) = 3,5
𝐻(−2|3,5)
𝑥1 = 4
𝑓(4) = −10
𝑇(4|−10)
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
12
ad c)
Im Intervall ]−∞; 1[ nimmt die Steigung
der Funktion 𝑓 ab.
In diesem Bereich ist 𝑓 ′ streng monoton
fallend und 𝑓 ′′ (𝑥) < 0.
In diesem Bereich ist 𝑓 rechtsgekrümmt
(negativ gekrümmt).
Im Intervall ]1; ∞[ nimmt die Steigung
der Funktion 𝑓 zu.
In diesem Bereich ist 𝑓 ′ streng monoton
steigend und 𝑓 ′′ (𝑥) > 0
In diesem Bereich ist 𝑓 linksgekrümmt
(positiv gekrümmt).
Im Wendepunkt W ändert sich die
Krümmung und 𝑓 ′′ (𝑥) = 0.
Da 𝑓 ′′ die Ableitung von 𝑓 ′ ist bedeutet
die Gleichung 𝑓 ′′ (𝑥) = 0, dass 𝑓 ′ sein
lokales Minimum oder Maximum bei der
wendestelle hat. Bei der Wendestelle hat
𝑓 somit, die minimale oder maximale
Steigung.
1
∙ (𝑥 3 − 3𝑥 2 − 24𝑥)
8
1
𝑓 ′ (𝑥) = ∙ (3𝑥 2 − 6𝑥 − 24)
8
1
𝑓 ′ (𝑥) = ∙ (6𝑥 − 6)
8
𝑓(𝑥) =
𝑓 ′′ (𝑥) = 0 →
𝑥=1
1
∙ (6𝑥 − 6) = 0 → 6𝑥 − 6 = 0 → 𝑥 = 1
8
𝑓(1) = −3,25
𝑊(1|3,25)
Beachte:
Beim lokalen Maximum ist die Funktion 𝑓 rechtsgekrümmt, also 𝑓 ′′ (𝑥) < 0
Beim lokalen Minimum ist die Funktion 𝑓 linksgekrümmt, also 𝑓 ′′ (𝑥) > 0
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
ad d)
Ist 𝑓 punktsymmetrisch, also 𝑓(−𝑥) = −𝑓(𝑥) ?
1
1
∙ ((−𝑥)3 − 3 ∙ (−𝑥)2 − 24 ∙ (−𝑥)) = ∙ (−𝑥 3 − 3𝑥 2 + 24𝑥)
8
8
1
1
−𝑓(𝑥) = − ∙ (𝑥 3 − 3𝑥 2 − 24𝑥) = ∙ (−𝑥 3 + 3𝑥 2 + 24𝑥)
8
8
𝑓(−𝑥) ≠ −𝑓(𝑥)
𝑓(−𝑥) =
ad e)
1
1
3 24
∙ (𝑥 3 − 3𝑥 2 − 24𝑥) = lim ∙ 𝑥 ∙ (1 − − 2 ) = −∞
𝑥→−∞
𝑥→−∞ 8
𝑥→−∞ 8
𝑥 𝑥
1
1
3 24
lim 𝑓(𝑥) = lim ∙ (𝑥 3 − 3𝑥 2 − 24𝑥) = lim ∙ 𝑥 ∙ (1 − − 2 ) = ∞
𝑥→∞
𝑥→∞ 8
𝑥→∞ 8
𝑥 𝑥
lim 𝑓(𝑥) = lim
Eine Funktion 𝑓 hat an der Stelle 𝑥 ein lokales Minimum, wenn 𝑓 ′ (𝑥) = 0 ∧ 𝑓 ′′ (𝑥) > 0
Eine Funktion 𝑓 hat an der Stelle 𝑥 ein lokales Maximum, wenn 𝑓 ′ (𝑥) = 0 ∧ 𝑓 ′′ (𝑥) < 0
Es sei 𝑓: 𝐴 → ℝ: 𝑥 ↦ 𝑓(𝑥) eine reelle Funktion und 𝐼 ⊆ 𝐴 ein Intervall. Dann gilt:
𝑓 ist streng monoton fallend in 𝐼, wenn 𝑓 ′ (𝑥) < 0 für alle inneren Stellen 𝑥 ∈ 𝐼
𝑓 ist streng monoton steigend in 𝐼, wenn 𝑓 ′ (𝑥) < 0 für alle inneren Stellen 𝑥 ∈ 𝐼
Eine Funktion 𝑓 hat an der Stelle 𝑥 einen Wendepunkt, wenn 𝑓 ′′ (𝑥) = 0 ∧ 𝑓 ′′′ (𝑥) ≠ 0
Es sei 𝑓: 𝐴 → ℝ: 𝑥 ↦ 𝑓(𝑥) eine reelle Funktion und 𝐼 ⊆ 𝐴 ein Intervall. Dann gilt:
𝑓 ist rechtsgekrümmt (negativ gekrümmt) in 𝐼, wenn 𝑓 ′′ (𝑥) < 0 für alle inneren
Stellen 𝑥 ∈ 𝐼
𝑓 ist linksgekrümmt (positiv gekrümmt) in 𝐼, wenn 𝑓 ′′ (𝑥) > 0 für alle inneren
Stellen 𝑥 ∈ 𝐼
13
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
14
Bsp5:
𝑓(𝑥) = 𝑥 3
𝑓 ′ (𝑥) = 3 ∙ 𝑥 2
𝑓 ′′ (𝑥) = 6 ∙ 𝑥
Es gilt 𝑓 ′ (0) = 0.
Trotzdem hat die Funktion 𝑓 im Nullpunkt kein lokales Minimum
oder lokales Maximum, sondern einen sogenannten Sattelpunkt
(Terrassenpunkt).
Die Bedingung 𝑓 ′ (𝑥) = 0 ist für das Vorliegen eines lokalen
Minimums oder lokalen Maximums nur notwendig, aber nicht
hinreichend.
Damit an einer Stelle 𝑥 ein lokales Minimum oder Maximum
vorliegt muss zusätzlich zur Bedingung 𝑓 ′ (𝑥) = 0 gelten, dass
𝑓 ′′ (0) ≠ 0
Bsp6:
𝑓(𝑥) = 𝑥 4
𝑓 ′ (𝑥) = 4 ∙ 𝑥 3
𝑓 ′′ (𝑥) = 12 ∙ 𝑥 2
𝑓 ′′′ (𝑥) = 24 ∙ 𝑥
Es gilt 𝑓 ′′ (0) = 0.
Trotzdem hat die Funktion 𝑓 im Nullpunkt keinen Wendepunkt.
Die Bedingung 𝑓 ′′ (𝑥) = 0 ist für das Vorliegen eines Wendepunkts
nur notwendig, aber nicht hinreichend.
Damit an einer Stelle 𝑥 ein Wendepunkt vorliegt muss zusätzlich
zur Bedingung 𝑓 ′′ (𝑥) = 0 gelten, dass 𝑓 ′′′ (0) ≠ 0
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
15
Bsp7:
1 4
𝑥 + 𝑥2 − 2
32
Bestimme die Nullstellen.
Ermittle die Monotoniebereiche und lokalen Extremstellen.
Ermittle die Krümmungsbereiche und Wendestellen.
Ist die Funktion achsensymmetrisch oder punktsymmetrisch?
Wie verhält sich die Funktion für 𝑥 → ±∞ ?
𝑓(𝑥) = −
a)
b)
c)
d)
e)
Bsp8:
Von der Aussichtsplattform eines Aussichtsturmsturms (ℎ0 = 150𝑚) wird ein Kieselstein mit 𝑣0 = 20𝑚/𝑠 empor geschleudert. Die Funktion ℎ gibt die Flughöhe ℎ(𝑡) (in m)
in Abhängigkeit der Zeit t (in s) wieder.
𝑔
ℎ(𝑡) = ℎ0 + 𝑣0 ∙ 𝑡 − ∙ 𝑡 2
𝑔 = 9,81 𝑚⁄𝑠 2
2
a) Berechne die mittlere Änderungsrate in den Intervallen [1,5; 2] und [7; 7,5]. Was
beschreibt die mittlere Änderungsrate im Kontext?
b) Gib eine Formel für die Änderungsrate an.
Was beschreibt die Änderungsrate im Kontext?
c) Berechne die Aufprallgeschwindigkeit?
a) Wie lange dauert es bis der Stein am Boden gelandet ist? Wie groß ist die maximale
Höhe und wann ist sie erreicht?
d) Berechne die zweite Ableitung. Was beschreibt die zweite Ableitung im Kontext?
e) Zeichne den Graphen der Funktion ℎ und ℎ′ . Interpretiere jeweils deren Verlauf.
Beachte:
Die Geschwindigkeit beschreibt die Änderung des Weges in Abhängigkeit der Zeit.
Die Beschleunigung beschreibt die Änderung der Geschwindigkeit in Abhängigkeit der
Zeit.
Die Beschleunigung 𝑎 ist die Ableitung der Geschwindigkeitsfunktion 𝑣 und zugleich die
zweite Ableitung der Wegfunktion 𝑠.
𝑣(𝑡) = 𝑠 ′ (𝑡)
𝑎(𝑡) = 𝑣 ′ (𝑡) = 𝑠 ′′ (𝑡)
Bsp9:
𝑑𝑠
𝑑𝑡
𝑑𝑣
𝑎=
𝑑𝑡
𝑣=
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
16
Ordne den gegebenen Funktionsgraphen die Graphen der entsprechenden Ableitungsfunktion zu.
Funktionsgraphen:
A
Graphen der Ableitungen
Bsp10:
B
C
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
17
Der Graph einer Polynomfunktion 𝑓 4. Grades ist gegeben. Ermittle die Funktionsgleichung von 𝑓.
𝑓(𝑥) = 𝑎 ∙ 𝑥 4 + 𝑏 ∙ 𝑥 3 + 𝑐 ∙ 𝑥 2 + 𝑑 ∙ 𝑥 + 𝑒
Da f symmetrisch zur 𝑦 - Achse ist, gilt:
𝑓(−𝑥) = 𝑓(𝑥)
Deshalb muss 𝑓 folgende Gestalt haben:
𝑓(𝑥) = 𝑎 ∙ 𝑥 4 + 𝑐 ∙ 𝑥 2 + 𝑒
Der Schnittpunkt mit der y - Achse ist
(0|2), weshalb 𝑒 = 2
Der Punkt (2|−2) ist ein lokales Minimum
von 𝑓 und somit ist 𝑓 ′ (2) = 0. Zudem gilt
natürlich 𝑓(2) = −2
𝑓(𝑥) = 𝑎 ∙ 𝑥 4 + 𝑐 ∙ 𝑥 2 + 𝑒
𝑓 ′ (𝑥) = 4𝑎 ∙ 𝑥 3 + 2𝑐 ∙ 𝑥
𝑓(2) = −2
𝑎 ∙ 24 + 𝑐 ∙ 22 + 2 = −2
𝑓 ′ (2) = 0
4𝑎 ∙ 23 + 2𝑐 ∙ 2 = 0
16 ∙ 𝑎 + 4 ∙ 𝑐 = −4
32 ∙ 𝑎 + 4 ∙ 𝑐 = 0
−16 ∙ 𝑎 = −4
𝑎=
1
4
1
32 ∙ + 4 ∙ 𝑐 = 0
4
𝑓(𝑥) =
→
4 ∙ 𝑐 = −8
1 4
∙ 𝑥 − 2 ∙ 𝑥2 + 2
4
→
𝑐 = −2
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
1.3 Weitere Ableitungsregeln
Bsp1:
1
𝑥
1
2) 𝑓(𝑥) = 3
𝑥
1) 𝑓(𝑥) =
3) 𝑓(𝑥) = √𝑥
4)
𝑓(𝑥) = 𝑥 ∙ √𝑥
5)
𝑓(𝑥) = 𝑥 2 ∙ √𝑥
6)
𝑓(𝑥) = √√𝑥
3
Ableitungen spezieller Funktionen:
𝑓(𝑥) = 𝑠𝑖𝑛(𝑥)
𝑓 ′ (𝑥) = 𝑐𝑜𝑠(𝑥)
𝑓(𝑥) = 𝑐𝑜𝑠(𝑥)
𝑓 ′ (𝑥) = −𝑠𝑖𝑛(𝑥)
𝑓(𝑥) = 𝑒 𝑥
𝑓 ′ (𝑥) = 𝑒 𝑥
𝑓(𝑥) = 𝑙𝑛(𝑥)
𝑓 ′ (𝑥) =
𝑓 =𝑢∙𝑣
𝑓 ′ = 𝑢′ ∙ 𝑣 + 𝑢 ∙ 𝑣 ′
1
𝑥
Produktregel
Bsp2:
1) 𝑓(𝑥) = 𝑠𝑖𝑛(𝑥) ∙ 𝑐𝑜𝑠(𝑥)
4) 𝑦 = 4𝑥 ∙ 𝑠𝑖𝑛(𝑥) ∙ 𝑐𝑜𝑠(𝑥)
2) 𝑓(𝑥) = 𝑥 ∙ 𝑠𝑖𝑛(𝑥)
5) 𝑦 = 𝑥 ∙ 𝑒 𝑥
3) 𝑓(𝑥) = 𝑥 2 ∙ 𝑐𝑜𝑠(𝑥)
6) 𝑦 = 𝑥 ∙ 𝑙𝑛(𝑥)
𝑓=
𝑢
𝑣
𝑢′ ∙ 𝑣 − 𝑢 ∙ 𝑣 ′
𝑓 =
𝑣2
′
Quotientenregel
Bsp3: Bestimme die Definitionsmenge und die Ableitung.
𝑥
2𝑥 − 4
1) 𝑦 =
4) 𝑓(𝑥) = 2
2
1+𝑥
𝑥 −4
2) 𝑦 =
𝑥 2 − 4𝑥 + 4
2𝑥 2 − 4𝑥
5) 𝑓(𝑥) =
3𝑥 2 + 2
(𝑥 − 2)2
18
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
19
Bsp4:
Zeige die Richtigkeit folgender Ableitungsregel für die Tangensfunktion
′
(𝑡𝑎𝑛(𝑥)) =
1
= 1 + 𝑡𝑎𝑛2 (𝑥)
2
(𝑥)
𝑐𝑜𝑠
𝑓 ′ (𝑥) = 𝑔′ (ℎ(𝑥)) ∙ ℎ′ (𝑥)
𝑓(𝑥) = 𝑔(ℎ(𝑥))
z.B.:
𝑓(𝑥) = 𝑠𝑖𝑛(2𝑥 + 3)
𝑓
′ (𝑥)
→
ℎ(𝑥) = 2𝑥 + 3
Kettenregel
𝑔(𝑧) = 𝑠𝑖𝑛(𝑧)
= 𝑐𝑜𝑠(2𝑥 + 3) ∙ 2
Bsp5:
1) 𝑓(𝑥) = (𝑥 2 − 4)2
4) 𝑦 = √5𝑥 2 + 3𝑥 − 4
2) 𝑓(𝑥) = (𝑥 2 − 4)3
5) 𝑦 = 3√2𝑥 2 − 3
3) 𝑓(𝑥) = (2𝑥 + 4)4
6) 𝑦 2 = 9𝑥 ∙ (4 − 𝑥)2
Bsp6:
1) 𝑓(𝑥) = 𝑠𝑖𝑛2 (𝑥)
2) 𝑓(𝑥) = 𝑠𝑖𝑛(𝑥 2 )
1
3) 𝑓(𝑥) = 𝑠𝑖𝑛 ( )
𝑥
Bsp7:
1) 𝑦 = 𝑠𝑖𝑛(2𝑥) ∙ 𝑒 −0,3𝑥
2) 𝑦 =
1
√2𝜋
1 2
∙ 𝑒 −2𝑥
Bsp8: Bestimme die Definitionsmenge und die Ableitung.
3𝑥 − 1
(3𝑥 − 2)2
𝑥
2) 𝑦 = −
√1 + 𝑥 2
1) 𝑦 =
𝑧 = ℎ(𝑥)
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
20
Bsp8:
Die „Königsdisziplin“ der Leichtathletik ist bei den Männern der Zehnkampf. Dabei erhält jeder Athlet in jeder der zehn Disziplinen Punkte, die für jede Disziplin nach einer
eigenen Formel errechnet werden. Für den Weitsprung gilt folgende Formel:
𝑝 = 0,14354 ∙ (𝑥 − 220)1,4
Dabei ist 𝑥 die Sprungweite in cm und 𝑝 die Punktezahl (auf Ganze gerundet). Der Weltrekord im Weitsprung liegt bei 895 cm. Der Weltrekord im Zehnkampf wurde von
Roman Šebrle 2001 beim Leichtathletikmeeting in Götzis aufgestellt und liegt bei 9 026
Punkten. Seine Weitsprungleistung betrug dabei 811 cm.
a) Berechne, wie viele Punkte Roman Šebrle mehr erhalten hätte, wenn er die Weltrekordweite gesprungen wäre!
b) Begründe mit der Formel, warum erst Sprünge ab 220 cm einen Punktwert ergeben.
c) Eine Sprungleistungssteigerung um 84 cm bringt nicht von jedem Ausgangswert den
gleichen durchschnittlichen Punktezuwachs (in Punkten/cm). Zeigen Sie das für die
Intervalle [500 cm; 584 cm] und [811 cm; 895 cm] durch eine Rechnung.
d) Begründen Sie mithilfe der untenstehenden Graphik, warum ein absolut gleicher
Weitenzuwachs für größere Ausgangswerte mehr Punkte bringt als für kleinere Ausgangswerte.
e) Gib eine Formel für die mittlere Änderungsrate und die Änderungsrate an und erläutere deren Bedeutung im Kontext dieser Aufgabe.
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
21
Bsp9: Exponentielle Abnahme
Balduin ist mit seinen Freunden im Gasthaus. Einer seiner Freunde bestellt ein Bier und
bekommt in diesem Augenblick einen Anruf. Aus Langeweile beobachtet Balduin wie der
Schaum im Bierglas seines Freundes abnimmt. Zu Hause untersucht Balduin das Phänomen der Abnahme des Bierschaums genauer. Anfangs ist der Schaum im Glas 7,20 cm
hoch. Nach einer Minute beträgt die Schaumhöhe noch 3,96 cm.
a) Beschreibe den Bierschaumzerfall mit der natürlichen Exponentialfunktion.
b) Berechne die mittlere Änderungsrate in den Intervallen [0; 1,5] und [1,5; 3]. Was
beschreibt die mittlere Änderungsrate im Kontext?
c) Berechne die Abnahmegeschwindigkeit zu den Zeitpunkten 𝑡 = 0, 𝑡 = 1.5 und 𝑡 = 3.
d) Nach wie vielen Sekunden unterschreitet die Bierschaumhöhe einen Wert von 1 cm?
e) Zeichne die Graphen der Zerfallsfunktion und ihrer Ableitung im Bereich [0; 6]. interpretiere das Krümmungsverhalten von 𝑓 im Kontext.
Beachte:
Ein exponentieller Abnahmeprozess wird allgemein durch folgende Funktion beschrieben.
𝑚(𝑡) = 𝑚0 ∙ 𝑒 −𝜆∙𝑡
𝑚′ (𝑡) = 𝑚0 ∙ 𝑒 −𝜆∙𝑡 ∙ (−𝜆) = −𝜆 ∙ 𝑚(𝑡)
𝑚′ (𝑡) = −𝜆 ∙ 𝑚(𝑡)
Die Änderungsrate zu einem Zeitpunkt 𝑡 ist direkt proportional der zu diesem Zeitpunkt
vorhandenen Menge.
𝑚′ (𝑡) beschreibt die Abnahmegeschwindigkeit. Die Abnahmegeschwindigkeit ist zunächst groß, da 𝑚(𝑡) noch groß ist und verlangsamt sich zusehends, da 𝑚(𝑡) immer
kleiner wird.
Für einen exponentiellen Wachstumsprozess gilt:
𝑚(𝑡) = 𝑚0 ∙ 𝑒 𝜆∙𝑡
𝑚′ (𝑡) = 𝜆 ∙ 𝑚(𝑡)
𝑚′ (𝑡) beschreibt die Wachstumsgeschwindigkeit. Die Wachstumsgeschwindigkeit ist
zunächst klein, da 𝑚(𝑡) noch klein ist und vergrößert sich zusehends, da 𝑚(𝑡) immer
größer wird.
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
22
Bsp10: Begrenztes Wachstum
Balduin nimmt ein Bier aus dem Kühlschrank. Zu Beginn hat das Bier eine Temperatur
von 𝑇2 = 5°𝐶. Die Umgebung hat eine Temperatur von 𝑇1 = 20°𝐶. Nach einer Minute hat
das Bier eine Temperatur von 6,2°C. Die Änderung der Temperatur ist proportional zur
Differenz der Umgebungstemperatur und der Temperatur der Flüssigkeit. Die
Temperatur des Bieres wird durch die Funktion 𝑓 beschrieben.
𝑓(𝑡) = 𝑇1 − (𝑇1 − 𝑇2 ) ∙ 𝑒 −𝑘∙𝑡
a) Berechne die Konstante 𝑘.
b) Berechne die mittlere Änderungsrate in den Intervallen [0; 5] und [30; 35].
Was beschreibt die mittlere Änderungsrate im Kontext?
c) Berechne die Änderungsrate zu den Zeitpunkten 𝑡 = 10 und 𝑡 = 35.
Welche Bedeutung kommt der Änderungsrate im Kontext dieser Aufgabe zu?
d) Zeige durch Einsetzen der Termdarstellung, dass 𝑓 ′ (𝑡) = 𝑘 ∙ (𝑇1 − 𝑓(𝑡))
e) Falls das Bier eine Temperatur von 15° C erreicht, stuft Balduin das Bier als lau ein
und mag es nicht mehr. Wie viel Zeit bleibt ihm sein Bier zu trinken?
f) Wann wird sich theoretisch die Temperatur des Biers der Umgebungstemperatur
angleichen?
g) Zeichne die Graphen der Funktionen 𝑓 und 𝑓 ′ im Bereich [0; 35]. Interpretiere das
Krümmungsverhalten von 𝑓 im Kontext.
Beachte:
𝑓 ′ (𝑡) = 𝑘 ∙ (𝑇1 − 𝑓(𝑡))
Wenn die Temperatur nahe bei 𝑇2 liegt, ist der Faktor (𝑇1 − 𝑓(𝑡)) groß und die Geschwindigkeit der Erwärmung ist ebenfalls groß. Wird 𝑓(𝑡) kleiner, so wird auch der
Faktor (𝑇1 − 𝑓(𝑡)) kleiner und folglich verlangsamt sich die Temperaturzunahme.
Nähert sich schließlich die Temperatur an 𝑇1 an, so geht der Faktor (𝑇1 − 𝑦(𝑡)) gegen
Null und die Temperaturzunahme ist sehr klein.
Mag. Raimund Hermann
Differenzialrechnung Schulübung 7i 1314
23
Bsp11: Logistisches Wachstum
Eine Population von 1000 Grönlandwalen lebt in einem abgegrenzten Lebensraum des nördlichen Eismeeres. Da die Wale keine natürlichen Feinde haben
und in ihrem Lebensraum ein reichhaltiges Nahrungsangebot vorfinden werden sie sich zunächst
rasch vermehren. Durch die Zunahme an Walen sinkt
aber das Nahrungsangebot, da das als Nahrung dienende Plankton nicht in unbeschränkter Menge zur
Verfügung steht. Die Wale können sich nicht mehr mit der anfänglichen Wachstumsgeschwindigkeit vermehren. Somit bietet das nördliche Eismeer nur einer begrenzten Anzahl S von Grönlandwalen Lebensraum. Diese Zahl liegt nach vorsichtigen Schätzungen
bei 10000 Tieren. Nach einem Jahr werden 1150 Wale gezählt. Die Anzahl der Wale wird
durch die Funktion 𝑓 beschrieben.
𝑓(𝑡) =
𝑎∙𝑆
𝑎 + (𝑆 − 𝑎) ∙ 𝑒 −𝑆∙𝑘∙𝑡
𝑓 ′ (𝑡) = 𝑘 ∙ 𝑓(𝑡) ∙ (𝑆 − 𝑓(𝑡))
a) Bestimme die Termdarstellung von 𝑓.
b) Berechne die mittlere Änderungsrate in den Intervallen [0; 5] und [30; 35].
Was beschreibt die mittlere Änderungsrate im Kontext?
c) Berechne die Änderungsrate zu den Zeitpunkten 𝑡 = 10 und 𝑡 = 35.
Welche Bedeutung kommt der Änderungsrate im Kontext dieser Aufgabe zu?
d) Wann erreicht die Wachstumsgeschwindigkeit ihr Maximum? Berechne den Wendepunkt und interpretiere das Krümmungsverhalten von 𝑓 im Kontext.
e) Zeichne die Graphen der Funktionen 𝑓 und 𝑓 ′ im Bereich [0; 35]
Beachte:
𝑓 ′ (𝑡) = 𝑘 ∙ 𝑓(𝑡) ∙ (𝑆 − 𝑓(𝑡))
Wenn die Population wächst, also 𝑓(𝑡) größer wird, bleibt zunächst der Ausdruck
(𝑆 − 𝑦(𝑡)) noch recht groß und die Population wächst rasch an. Wird jedoch
𝑦(𝑡) immer größer, so wird der Faktor (𝑆 − 𝑦(𝑡)) immer kleiner und die Wachstumsgeschwindigkeit verlangsamt sich. Nähert sich schließlich die Populationsgröße 𝑦(𝑡) der
Sättigungsgrenze 𝑆 an, so wird der Faktor (𝑆 − 𝑦(𝑡)) fast Null und die Wachstumsgeschwindigkeit ist sehr klein.