Info – Differenzialrechnung Die mittlere oder durchschnittliche

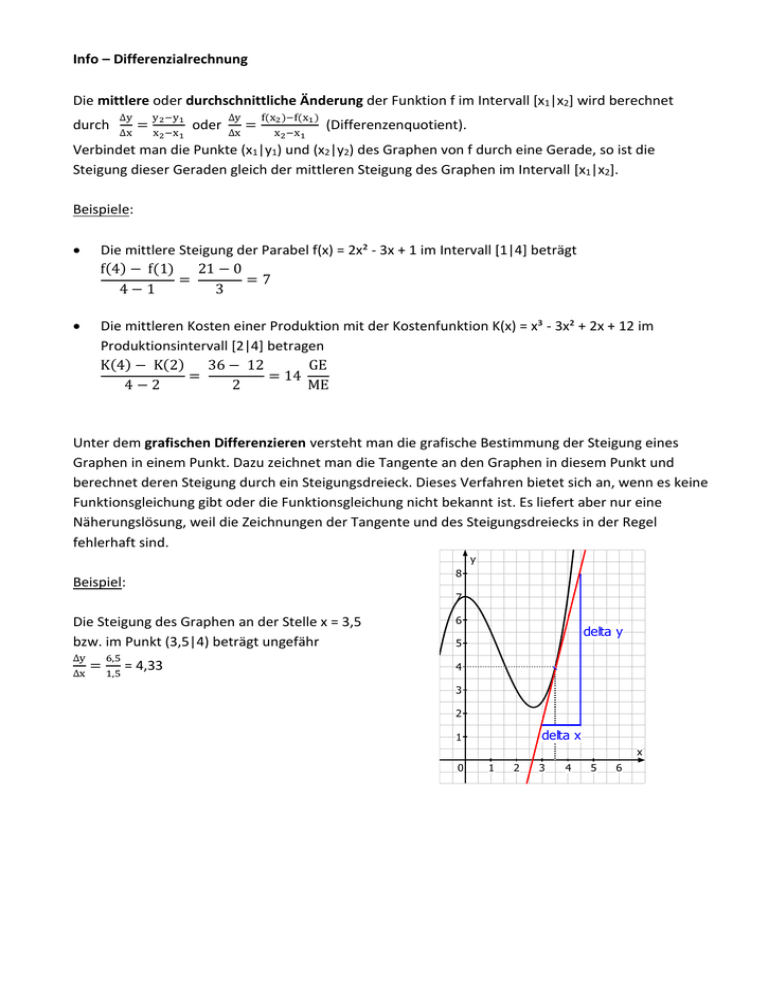
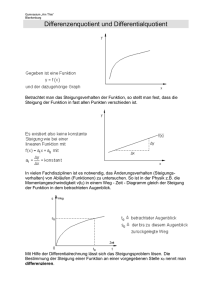
Info – Differenzialrechnung
Die mittlere oder durchschnittliche Änderung der Funktion f im Intervall [x1|x2] wird berechnet
durch
∆y
∆x
y −y
= x2 −x1 oder
2
1
∆y
∆x
=
f(x2 )−f(x1 )
x2 −x1
(Differenzenquotient).
Verbindet man die Punkte (x1|y1) und (x2|y2) des Graphen von f durch eine Gerade, so ist die
Steigung dieser Geraden gleich der mittleren Steigung des Graphen im Intervall [x1|x2].
Beispiele:

Die mittlere Steigung der Parabel f(x) = 2x² - 3x + 1 im Intervall [1|4] beträgt
f(4) − f(1)
21 − 0
=
=7
4−1
3

Die mittleren Kosten einer Produktion mit der Kostenfunktion K(x) = x³ - 3x² + 2x + 12 im
Produktionsintervall [2|4] betragen
K(4) − K(2)
36 − 12
GE
=
= 14
4−2
2
ME
Unter dem grafischen Differenzieren versteht man die grafische Bestimmung der Steigung eines
Graphen in einem Punkt. Dazu zeichnet man die Tangente an den Graphen in diesem Punkt und
berechnet deren Steigung durch ein Steigungsdreieck. Dieses Verfahren bietet sich an, wenn es keine
Funktionsgleichung gibt oder die Funktionsgleichung nicht bekannt ist. Es liefert aber nur eine
Näherungslösung, weil die Zeichnungen der Tangente und des Steigungsdreiecks in der Regel
fehlerhaft sind.
y
Beispiel:
8
7
Die Steigung des Graphen an der Stelle x = 3,5
bzw. im Punkt (3,5|4) beträgt ungefähr
∆y
∆x
6,5
= 1,5 = 4,33
6
delta y
5
4
3
2
delta x
1
x
0
1
2
3
4
5
6
Strebt x gegen 0 (Schreibweise x  0) erhält man die punktuelle oder lokale Änderung an der
lim f(x+∆x)− f(x)
Stelle x: f ′ (x) =
(Differenzialquotient)
∆x
x → 0
(In der Mathematik ist ein Differenzial eine unendlich kleine Differenz.)
f‘(x) (sprich „f Strich von x“) heißt auch Ableitung von f. Die Ableitung gibt die Steigung bzw. die
Änderung des Graphen von f an der Stelle x bzw. im Punkt (x|f(x)) an. Geometrisch ist die Ableitung
f‘(x) gleich der Steigung der Tangente an den Graphen von f im Punkt (x|f(x)).
Beispiele:

f(x) = x²  f‘(x) = 2x, d.h. die Steigung der Parabel f(x) = x² an der Stelle x beträgt 2x.

Die Steigung der Parabel f(x) = x² an der Stelle x = 3 beträgt demnach f‘(3) = 23 = 6.

Die Steigung der Parabel f(x) = x² im Punkt (-2|f(-2)) beträgt demnach f‘(-2) = 2(-2) = - 4.

In welchem Punkt hat die Parabel die Steigung 8?
f‘(x) = 8
Die Steigung beträgt 8, gesucht ist die entsprechende Stelle x.
2x = 8
x=4
f(4) = 4² = 16
Der zugehörige y-Wert des Punktes ist der Funktionswert an der Stelle x = 4.

Die Tangente an die Parabel im Punkt (-1|1) hat die Steigung f‘(-1) = 2(-1) = -2.
Ableitungsregeln

Ein konstanter Summand fällt beim Ableiten weg.
Beispiele: f(x) = x2 + 3  f‘(x) = 2x
f(x) = - 2  f‘(x) = 0

Beim Ableiten einer Potenz wird die Hochzahl zum Faktor und die neue Hochzahl ist um 1 kleiner als
die alte: f(x) = xn  f‘(x) = nxn-1 (Potenzregel)
Beispiele: f(x) = x4  f‘(x) = 4x4 - 1 = 4x3
f(x) = x  f‘(x) = 1x1 - 1 = x0 = 1

Ein konstanter Faktor bleibt beim Ableiten erhalten. (Faktorregel)
Beispiele: f(x) = 4x3  f‘(x) = 43x3 - 1 = 12x2
1
1
f(x) = - 2 x4  f‘(x) = - 2  4x4 - 1 = - 2x3

Die Ableitung einer Summe ist gleich der Summe der Ableitungen bzw. eine Summe wird
summandenweise abgeleitet. (Summenregel)
Beispiele: f(x) = 2x3 + 0,5x2 + 1  f‘(x) = 6x2 + x
f(x) = 0,25x3 - 2,5x2 + 3x – 5  f‘(x) = 0,75x2 - 5x + 3
Extrempunkte
H heißt relativer bzw. lokaler Hochpunkt oder Maximium, wenn es eine Umgebung um H gibt, in der H
der höchste Punkt ist. Ein absoluter Hochpunkt ist der höchste Punkt des Graphen.
T heißt relativer bzw. lokaler Tiefpunkt oder Minimum, wenn es eine Umgebung um T gibt, in der T der
niedrigste Punkt ist. Ein absoluter Tiefpunkt ist der niedrigste Punkt des Graphen.
In Hoch- und Tiefpunkten ist die Steigung 0.
Berechnung von Extrempunkten:
Ist f ’(xH) = 0 und f ’’(xH) < 0, dann ist H(xH|f(xH)) relativer Hochpunkt des Graphen von f.
Ist f ’(xT) = 0 und f ’’(xH) > 0, dann ist T(xT|f(xT)) relativer Tiefpunkt des Graphen von f.
oder
Ist f ’(xH) = 0 und hat f ’ an der Stelle xH einen Vorzeichenwechsel von + nach –, dann ist H(xH|f(xH))
relativer Hochpunkt des Graphen von f.
Ist f ’(xT) = 0 und hat f ’ an der Stelle xT einen Vorzeichenwechsel von – nach +, dann ist T(xT|f(xT))
relativer Tiefpunkt des Graphen von f.
Beispiele:
 f(x) = x3 - 3x2
 f‘(x) = 0
3x² - 6x = 0
x1 = 2 und x2 = 0  mögliche Extremstellen
 Ergebnisse aus  in f‘‘(x) einsetzen, um auf Hoch- oder Tiefpunkt zu untersuchen:
f‘‘(2) = 62 – 4 = 8 > 0, d.h. T bei x = 2
f‘‘(0) = – 4 < 0, d.h. H bei x = 0
 Ergebnisse aus  in f(x) einsetzen, um die y-Koordinaten zu berechnen:
f(2) = 2³ - 32² = 0 , d.h. T(2|-4)
Graph siehe unten
f(0) = 0, d.h. H(0|0)

f(x) = x4
 f‘(x) = 0
4x³ = 0
x1 = 0  mögliche Extremstelle
 Ergebnisse aus  in f‘‘(x) einsetzen, um auf Hoch- oder Tiefpunkt zu untersuchen:
f‘‘(0) = 0, d.h. keine Aussage über Hoch- und Tiefpunkte möglich
Untersuchung von f‘ auf Vorzeichenwechsel an der Stelle x = 0:
f‘(-1) = 4(-1)³ = - 4, also negativ
f‘ hat an der Stelle x = 0 einen Vorzeichenwechsel
f‘(0) = 0
von – nach +, d.h. T bei x = 0
f‘(1) = 41 = 4, also positiv
 Ergebnisse aus  in f(x) einsetzen, um die y-Koordinaten zu berechnen:
f(0) = 0, d.h. T(0|0)
Wendepunkte
Die Punkte des Graphen von f, in denen die Steigung maximal oder minimal ist, heißen Wendepunkte.
Daraus ergibt sich, dass die Krümmung von f in den Wendepunkten wechselt.
Berechnung von Wendepunkten:
Die Wendestellen von f sind die Extremstellen von f‘.
Ist f ’‘(xW) = 0 und f ’‘’(xW) < 0, dann ist W(xW|f(xW)) ein Wendepunkt mit maximaler Steigung.
Ist f ’(xW) = 0 und f ’‘’(xW) > 0, dann ist W(xW|f(xW)) ein Wendepunkt mit minimaler Steigung.
Beispiele:
 f(x) = x3 - 3x2
 f‘‘(x) = 0
6x - 6 = 0
x=1
 Ergebnisse aus  in f‘‘‘(x) einsetzen:
f‘‘‘(1) = 6 > 0, d.h. W mit minimaler Steigung bei x = 1
 Ergebnis aus  in f(x) einsetzen, um die y-Koordinate zu berechnen:
f(1) = 1³ - 31² = - 2 , d.h. W(2|- 2)
H
-1
0
f(x) = x³ - 3x²
1
2
-1
-2

3
f(x) = - x³ + 3x² - 3x + 3
4
3
W
2
-3
-4
x
Sa
1
x
T
0
1
2
3
4
f(x) = - x³ + 3x² - 3x + 3
 f‘‘(x) = 0
– 6x + 6 =
x=1
 Ergebnisse aus  in f‘‘‘(x) einsetzen:
f‘‘‘(1) = – 6 < 0, d.h. W mit maximaler Steigung bei x = 1
 Ergebnis aus  in f(x) einsetzen, um die y-Koordinate zu berechnen:
f(1) = – 1³ + 31² – 31 + 3 = 2 , d.h. W(1|2)
Da auch f‘(0) = 0 ist, ist W ein Wendepunkt mit der Steigung 0.
Solche Punkte nennt man Terrassen- oder Sattelpunkte.
Graph siehe oben
Kurvendiskussion
Unter einer Kurvendiskussion versteht die Untersuchung einer Funktion auf charakteristische Punkte.
Das sind Nullpunkte, Extrempunkte und Wendepunkte. Abschließend werden die Ergebnisse in dem
Funktionsgraphen dargestellt.
Beispiel:
f(x) = x3 + 3x2 – 9x – 27
 Ableitungen
f‘(x) = 3x2 + 6x – 9
f‘‘(x) = 6x + 6
f‘‘‘(x) = 6
3.
 Nullpunkte
f(x) = 0
x3 + 3x2 – 9x – 27 = 0
x1 = 3 und x2 = - 3
N1(3|0) und N2(-3|0)
Schnittpunkt mit der y-Achse: Sy(0|-27)
 Wendepunkte
1. f‘’(x) = 0
x=-1
2. Ergebnisse aus 1. in f‘‘‘ einsetzen:
f‘‘‘(-1) = 6 > 0  Wendepunkt
mit minimaler Steigung bei x = - 1
3. Funktionswerte berechnen:
Ergebnisse aus 1. in f(x) einsetzen
f(-1) = (-1)3 + 3(-1)2 - 9(-1) – 27 = - 16
 W(-1|-16)
 Extrempunkte
1. f‘(x) = 0
x1 = 1 und x2 = - 3
2. Ergebnisse aus 1. in f‘‘(x) einsetzen:
f‘‘(1) = 61 + 6 = 12 > 0
 Tiefpunkt bei x = 1
f‘‘(-3) = 6(- 3) + 6 = - 12 < 0
 Hochpunkt bei x = - 3
-5
-4
HN
-3
Funktionswerte berechnen:
Ergebnisse aus 1. in f(x) einsetzen
f(1) = 13 + 312 - 91 – 27 = - 32
 T(1|-32)
f(-3) = 0 (siehe Nullpunkte)
 H(-3|0)
 Graph
Einteilung der Achsen an den berechneten
Koordinaten ausrichten.
y = f(x)
-2
-1
0
1
-10
W
-20
-30
-40
Sy
T
2
3
N
x