Reziproker_Raum(7)_neu

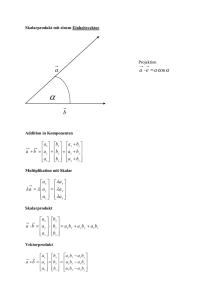
Die kristallographische Metrik
Gitterparameter: a, b, c, , , 
Positionsvektor:
 


r  xa  yb  zc  x
b
Bruchkoordinaten: x, y, z
y

a
 
z    b   XA
 c 
 
a





 




r1  r2  x1a  y1b  z1c  x2 a  y2b  z2c 
 x1x2 a 2  y1 y2b 2  z1z2c 2  x1 y2  x2 y1 ab cos   x1z2  x2 z1 ac cos    y1z2  y2 z1 bc cos 


     

a  a a  b a  c   x2 
a
a



       
 
 
 
r1  r2   x1 y1 z1    b   x2 y2 z2    b    x1 y1 z1    b  a b  b b  c    y2   X1ΓX 2
         
 c 
 c 
 
 
 c  a c  b c  c   z2 
Matrix (Tensor) der Metrik: 
1
Die kristallographische Metrik
Eigenschaften der -Matrix


det Γ  a 2b2c 2 1  cos2   cos 2   cos2   2 cos  cos  cos   V 2
Volumen der Elementarzelle:
  
V  abc 1  cos   cos   cos   2 cos  cos  cos   a  b  c
2
2
2
Länge des r-Vektors (Abstand von [0 0 0]):
2  
r  r  r  XΓX  x 2 a 2  y 2b 2  z 2 c 2  2 xyab cos   2 xzac cos   2 yzbc cos 
Abstände zwischen Atomen in Positionen (x1,y1,z1) und (x2,y2,z2):
 
 
  2
2
r1  r2  x  a 2  y 2 b 2  z 2 c 2  2xyab cos   2xzac cos   2yzbc cos 
x, y, z   x1  x2 , y1  y2 , z1  z2 
Winkel zwischen zwei Vektoren:
 
r1  r2
X ΓX
cos      1  2
r1  r2
r1  r2
2
Das reziproke Gitter
… ist analog zum Kristallgitter
Vektor im reziproken Gitter:




r  ua  vb  wc 
Definition der Basisvektoren im reziproken Raum (Gitter):
     
a  a  b b  c c 1
           
Senkrecht:
a b  a c  b  a  b c  c  a  c b  0
c
d(001)
b
a



  n100   n010   n001
a 
;b 
;c 
d100
d 010
d 001
 
 
 a  b
a b
ab sin  
c 
   
n001
V
V
a b c



c a
ca sin  
b    
n010
V
a b c
 

b c
bc sin  
a     
n100
V
a b c
3
Reziproke Gittervektoren
Triklin:

bc sin 
V
a 
; sin   
V
abc sin  sin 
  ca sin 
V
b 
; sin   
V
abc sin  sin 

ab sin 
V
c 
; sin   
V
abc sin  sin 
V  abc sin  sin  sin  * 
 abc sin  sin  * sin  
 abc sin  * sin  sin 
V  abc 1  cos 2   cos 2   cos 2   2 cos  cos  cos 
 1 

1
1
a

;
b

;
c

;       90 ;    180   ; V  abc sin 
Monoklin:
a sin 
b
c sin 
 1  1 

1

Orthogonal (orthorhombisch, a  ; b  ; c  ;         90; V  abc
a
b
c
tetragonal, kubisch):
Hexagonal:



2
1
3
a b 
; c   ;       90 ;    60 ; V  abc
c
2
a 3
Rhomboedrisch :


a  b   c  
sin 
a 1  3 cos 2   2 cos 3 
;         ; cos    
cos 
1  cos 
4
Das reziproke Gitter
… ist analog zum Kristallgitter (im direkten Raum)

  
Ghkl  ha  kb  lc
c*
003
103
203
002
102
202
001
101
201
100
000
303
302
403
a*, b*, c* … Basisvektoren des
reziproken Gitters
402
301
401
200
300
400
_
001
_
101
_
201
_
301
_
401
_
002
_
102
_
202
_
302
_
402
_
003
_
103
_
203
_
303
_
403
a*
h, k und l … ganze Zahlen
(Miller Indizes)
Im (direkten) Kristallgitter




T  n1a  n2b  n3c
5
Eigenschaften der reziproken Vektoren
Vektor des reziproken Gitters, G=ha*+kb*+lc*, ist senkrecht zu den
Netzebenen mit den Miller Indexen (hkl)
Matrix (Tensor) der reziproken Metrik (der Metrik im reziproken
Raum): 
 a 
 a   a  a   b a   c  
 


  









Γ  b  a b c   a b b b b c 
 
  

 a  c b  c  c   c  
 c 


 


Winkel zwischen zwei Netzebenen (h1k1l1) und (h2k2l2) ist gleich dem
Winkel zwischen den entsprechenden Vektoren im reziproken Gitter:
 




G1  G2
G1  h1a  k1b  1c 

cos     ; 


G

h
a

k
b


c
G1  G2
2
2
2
2
6
Winkel zwischen Netzebenen
(Kristallflächen)
 




G1  G2
G1  h1a  k1b  1c 

cos     ; 


G2  h2 a  k2b   2c 
G1  G2
 
 
 
2  
2
2
2
G  G  G  h 2 a  k 2 b   2 c  2hkab cos    2hac cos  *  2kbc cos  





 




G1  G2  h1a   k1b    1c   h2 a   k 2b    2 c  
 
 
 
 h1h2 a   k1k 2 b   1 2 c   h1k 2  h2 k1 a b cos    h1 2  h2  1 a c  cos    k1 2  k 2  1 bc  cos  


     
 a   a  a   b  a   c    h2 
 a 
 a 
        
  
  
 
G1  G2  h1 k1  1    b   h2 k 2  2    b   h1 k1  1    b   a  b   b  b   c     k 2   H1 Γ  H 2
               
 c  
 c  
 
 
 c  a c b c c  2 
2
2
2
7
Winkel zwischen Netzebenen
Kubisch:
cos  
h1h2  k1k2  1 2
h12  k12  12  h22  k22   22
Orthorhombisch:
Hexagonal:
cos  
h1h2 k1k 2 1 2
 2  2
2
a
b
c
h12 k12 12
h22 k 22  22


 2 2 2
a2 b2 c2
a
b
c
cos  


2
 2  1 2
h1h2  k1k 2  12 h1k 2  k1h2  
  2
c
a 3

h12
 k12

2
 2  12
 h1k1 
  2
a 3 c

h22
 k 22

2
 2   22
 h2 k 2 
  2
c
a 3
8
Winkel zwischen Netzebenen im
kubischen Kristallsystem
cos  
h1h2  k1k2  1 2
h12  k12  12  h22  k22   22
9
Vektor des reziproken Gitters
 


G  ha  kb  c
2  
2
2
2
G  G  G  h 2 a   k 2 b   2 c  
 
c*
003
103
203
002
102
202
001
101
201
100
000
303
302
 2hkab cos    2hac cos  *  2kbc cos  
402
Länge des G-Vektors =
= Abstand vom Anfang des reziproken
Gitters
(G ist senkrecht zu den Netzebenen)
= reziproker Abstand zwischen den
Netzebenen
= reziproker Netzebenenabstand
301
401
200
300
400
_
101
_
201
_
301
_
401
_
002
_
102
_
202
_
302
_
402
_
003
_
103
_
203
_
303
_
403
2
d hk

 
 
403
_
001
1
 
 
a*
Die Punkte im reziproken Raum
entsprechen den Familien der Netzebenen
 
2
2
2
2
 G  h 2 a  k 2 b   2 c  2hkab cos    2hac cos  *  2kbc cos  
10
Konstruktion des reziproken Gitters
11
Netzebenenabstände
Kubisch:
1
2
d hk


h2  k 2  2
a
Orthorhombisch:
Trigonal:
Monoklin:
1
2
d hk


1
a2
1
2
d hk

h

1
2
d hk

Tetragonal:
2

2

h2
a
2

k2
b
2

2
c
2
Hexagonal:


1
2
d hk

1
2
d hk



h2  k 2
a
4
3a
 k 2   2 sin 2   2hk  h  k  cos 2   cos 
2
2
h
2

2
c2

 k  hk 
2

1  2 cos3   3 cos 2 
h2
a 2 sin 2 

k2
b2

2
c 2 sin 2 

2h cos 
ac sin 2 
12
2
c2
Periodizität im direkten und
reziproken Raum
13
http://www.ysbl.york.ac.uk/~cowtan/fourier/gallery.html
Periodizität im direkten und
reziproken Raum
14
Periodizität im direkten und
reziproken Raum
15
Periodizität im direkten und
reziproken Raum
16
Periodizität im direkten und
reziproken Raum
17
Periodizität im direkten und
reziproken Raum (eindimensional)

d


Konstruktive Interferenz der
Strahlung bei:
2d sin   n
Laue
Bedingungen
s  s0  a  h
  
s  s0  b  k
s  s0  c  
Braggsche Gleichung
18
Beugungsbedingungen
Face centred cubic
40
s  s0  a  h
  
s  s0  b  k
s  s0  c  
30
25
qz (A^-1)
Laue
Bedingungen:
35
Laue Bedingungen
im reziproken Raum:
Bragg Gleichung:
s  s0   G

2 sin 


1
d hk
15
10
5
s  s0   G

20
0
-20
hk
-10
0
qx (A^-1)
10
20
Interferenzmaximum wird beobachtet,
wenn der Beugungsvektor in einem
Punkt des reziproken Gitters endet
hk
; 2d hk sin   
sin 
s0

s

sin 
19
Ewald Kugel
20
Beugungsbedingung
Elastische Röntgenstreuung
(gleiche Wellenlänge oder
gleiche Energie):

s0



s
 
s  s0 
 Ghk

 

s  s0 2 sin 
1

 Ghk 


d hk

2d hk sin   

Änderung der Länge des
Beugungsvektors:
 
s0  s


2 sin 

Drehen des reziproken
Gitters:
s/
2
s0/
Drehen des Kristalls im
Primärstrahl.
21
Beugungsbedingung für
polykristalline Proben
Information über die
Orientierung des Kristalls ist
verloren
s/
2
s0/
Die Bragg Gleichung
beschreibt vollständig die
Beugungsbedingung für
polykristalline Proben
2d hk sin   
22