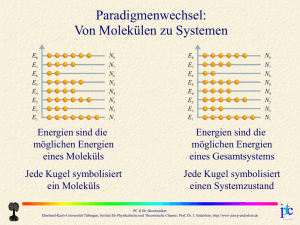
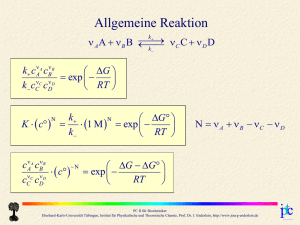
*************E

Grundgleichungen der Wellenfunktion
2
2
  2  2  2 



  U 
 2  2  2  U  
i t
2m  x
y
z 
2m
Laplace-Operator
Schrödingergleichung
Energieoperator


 E
i t
Hamiltonoperator
Hˆ  
Impulsoperator
2
2m
i
grad   p
 U
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Der quantenmechanische harmonische Oszillator
Gesucht:
Eigenzustände des
Hamiltonoperators
Teilchen im harmonischen
Potential (U = k∙x2/2):
Ĥ   x   E  x 
Gesamte Wellenfunktion:
 i 
  x, t     x  exp   Et 


2

d2 k 2 
 x    x   E  x 

2
 2m dx 2 
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Grundzustand des harmonischen Oszillators
2
2







x
d

x
ˆ
A0  x   exp  
 exp 
 0  x    0
 2  dx 
 2 

 x 2 
0  x   C exp  

2


 mx 2 
 m 
0  x   

 exp  

2




14
ĥ0  x   0  x 
E (J)
= 100 mm
m = 12 D

E0  x  
2
x (nm)
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
1. angeregter Zustand des harmonischen Oszillators
Aˆ  Aˆ  hˆ  
ˆ ˆ   hˆ  
AA

ˆ 0
A
0
ˆ ˆ   x  ?
Was ergibt hA
0

ˆ ˆ    x   Aˆ  Aˆ   Aˆ    x   Aˆ  AA
ˆ ˆ    x   Aˆ    x 
hA
0
0
0
0
ˆ ˆ   Aˆ  Aˆ  2
AA


ˆ ˆ    x   Aˆ  Aˆ  Aˆ  2   x   Aˆ    x   3Aˆ    x 
hA
0
0
0
0
ist neue Eigenfunktion
 d


ˆ
1  x  ~ A 0  x        0  x 
von ĥ mit Eigenwert 3!
 dx

3 
E1 
2
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
1. angeregter Zustand des harmonischen Oszillators
Aˆ  Aˆ  hˆ  
Normierung



ˆ ˆ   hˆ  
AA
 d


ˆ
1  x  ~ A 0  x        0  x 
 dx

dx  Aˆ  0  x    Aˆ  0  x   



ˆ ˆ    x    2
dx 0  x   AA
0

partielle Integration
 x 2  d 
 x 2  
1 ˆ
1
1  x  
A 0  x   
exp 
 exp  
 0 
2
2
 2  dx 
 2  
1  x 
 


14
 x 2  d
2


exp 
exp

x
 

2
 2  dx



m
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Höhere Zustände des harmonischen Oszillators
Aˆ  Aˆ  hˆ  
ˆ ˆ   hˆ  
AA
ˆ ˆ   Aˆ  Aˆ  2
 Aˆ , Aˆ    AA




 
ˆ ˆ   x  ~  Aˆ Aˆ    Aˆ   x   Aˆ  hˆ  2    x    2k  1 Aˆ   x 
hA
ˆ ˆ   x  ~  Aˆ Aˆ    Aˆ   x   Aˆ  hˆ  2    x    2k  1 Aˆ   x 
hA
ˆ ˆ    x  ~ Aˆ  Aˆ   Aˆ    x   Aˆ  hˆ  2   x   5Aˆ    x 
hA
1
1
1
1



k


k
k
k

k
k
k
k
Â+ und  sind sogenannte Leiteroperatoren: Â+ transformiert
Zustand in energetisch nächsthöheren, Â transformiert
Zustand in energetisch nächsttieferen Zustand
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Alle Zustände des harmonischen Oszillators
 
k  x  ~ Aˆ 
k
k

 x  d
 x  
0  x    1 exp 
 exp  
  0  x 
 2  dx
 2 

2
k
  
2
14
 x 2  d k
2


k  x  
1 exp 
exp

x


k


2 k n ! k
 2  dx

k
  
14
 x 2 
k  x  
exp  
 Hk
k
k
2 k !
 2 
 x
k
d
2


H x  z    1 exp z 2
exp

z
k 

dz
Hermitesche Polynome
k
 



1

Ek    k  
2


m
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Die untersten Zustände des harmonischen Oszillators
3  x  
Â
2  x  
Â

1  x  
Â
  
14
 x 2 
2
3 3
exp  
12

x

8

x

3
48
 2 
  
14
8
2

 x 2  2 2
exp  
 4 x  2
 2 



  
14
 x 2 
exp  
  2x 
2
 2 
0  x      
14
Â
 x 2 
exp  

 2 
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Â
Â
Die untersten Zustände des harmonischen Oszillators
2c


  1.99 1020 J

||2
x (nm)
x (nm)
Energie (J)
m = 12 D
 = 100 mm
Zahl der Nullstellen von 
(nodes) = k
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Wasserstoffatom
Potentielle Energie eines Elektrons im elektrischen Feld eines
positiv geladenen Protons:
q2

U r   

40 r
r
Klassische Bewegungsgleichungen
r  r r
r  r r
mp
d 2 rp
dt
2
 eˆ r
dU  r 
dr
e
p
e
dU  r 
d 2re
me 2  eˆ r
dt
dr
reduzierte Masse:
1
 1
1 
m

 me m p 


 1
d 2r
1  dU  r 
 eˆ r 


2

dt
 me m p  dr
dU  r 
d 2r
m 2  eˆ r
dt
dr
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
p
Wasserstoffatom
q2


Potentielle Energie U  r   
40 r
r
Reduzierte Masse
 1
1 
m

 me m p 


Zeitunabhängige
Wellenfunktion
1


f  r   f  r   Ef  r 
2m
r
2
Laplace-Operator in Kugelkoordinaten:
1 2
1
f 
rf

 2
2 
r r
r
 1 
f
1 2 f 
sin   2

2 
sin



sin




PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Intermezzo: Kugelkoordinaten
z
x  r sin  cos 

y  r sin  sin 
z  r cos 

y
x
eˆ  
 eˆ  
grad  eˆ r 

r r  r sin  
eˆ  
eˆ  

div  eˆ r 
sin  
r r sin  
r sin  
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Drehimpuls
Wellenfunktion bei Bewegung
um eine fixe Achse (z.B. z):
f ~ eim
Beschränkung:
f  r, ,   f  r, ,   2
m muß ganze Zahl sein!
Quantisierung des Drehimpulses:
Lz  m
Drehimpuls:
Impuls mal
Radius
Quantisierung des Drehimpulses gilt für jede Achse!!
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Drehimpuls um verschiedene Achsen
90°
90°
f ~ e i
f ~ ei  2  ei
f ~ e  i
f ~ e2i
f ~ e2i  3ei  6  3ei  e2i
f ~ e2i
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Wasserstoffatom: Trennung der
Variablenabhängigkeiten
2
2

rf  
2 
2mr r
2mr 2
2
 1 
f
1 2 f
sin   2

2
sin



sin



 
  f  Ef
 r
f ~ eim
2
2

rf  
2 
2mr r
2mr 2
2
Quadrat des
gesamten
Drehimpulses
L
K
 1 
f
m2
sin   2

 sin 
 sin  
 
f   f  Ef
 r
1 
f
m2
sin   2 f   Kf
sin  
 sin 
2
2
K


rf  
f  f  Ef
2 
2
2mr r
2mr
r
2
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Wasserstoffatom: -Abhängigkeit
1 
f
m2
sin   2 f   Kf
sin  
 sin 
2
sin
2
sin
K
2
 cos 2   sin   m2 sin
2


 1

 1 sin   m2 sin
m
Ansatz: f ~ sin 
2
   K sin 
2
   K sin 
Gesamtdrehimpuls ~ Drehimpuls um z
Generelle Lösung: f ~ Pm  cos 
Assoziierte Legendre-Polynome
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Assoziierte Legendre-Polynome
Pm  x  
 1
m
2 !

1  x2

m2
d m 2
x 1
m
dx


Pm  cos 
m=0
m=1
ℓ=0
ℓ=1
P0  P00  1
P1  P10  cos 
P11   sin 
ℓ=2
P2  P20  3cos 2   1 2 P21  3cos  sin  P22  3sin 2 


m=2
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Wasserstoffatom: -Abhängigkeit
m = -2
m = -1
m=0
m=1
m=2
ℓ=0
s
ℓ=1
p
ℓ=2
d
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Wasserstoffatom: r-Abhängigkeit
1 
f
m2
sin   2 f  
sin  
 sin 
f ~ Pm  cos  eim

2
 2  rf 
2m r
2

2

 1
r2
2m
Im Limes r → 0
r
2
~

 1
r
2
 1 f

 rf    rf   E   rf 
r
2
 2  rf 
Im Limes großer

~ E   rf 
2
Werte von r:
2m r
 2  rf 

  rf 
 2mE 
rf ~ exp  i
r 
2


 2mE 
rf ~ r exp  i
r 
2



1
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Wasserstoffatom: r-Abhängigkeit

2
 2  rf 
2m r
2

2

2m
Ansatz: rf ~ r



2m 
2
i
m

1
2mE
 1 2  2i
2
r
2mE  
E 1  
 1
r2
1

 rf    rf   E   rf 
r
 2mE 
exp  i
r 
2


 1 2mE 
 2 
r

m 2
2
2

 1
2

2

 1 1 
 E
2
2m
r
r
mq 4
32202
2

 1
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
2
Wasserstoffatom: Grundzustand
f1,0,0
 mq 2
 exp  
2
4

0

mq 4
E1  
322 02

 r 
r   exp   

 a0 
Bohr-Radius: a0 = 0.529 Å
2
E1  13.6 eV
Elektronenvolt: Energie, die ein Elektron bei Durchlaufen einer
Spannungsdifferenz von einem Volt erhält


1 eV  1.6022 1019 C  1 V   1.6022 1019 J
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Wasserstoffatom: Allgemeine Lösung
f n,
,m
 2r  2r  2 1  2r  m
im
 N exp  
L
P
cos

e


 n  1 
 
 na0  na0 
 na0 
Assoziierte
Laguerre-Polynome
 m , n
x k
p
e
x
d
 x pk
Lkp  x  
e
x
p
p ! dx

mq 4
En  
322 02 2 n 2
ℓ=0
n=2
L10  1
L11  2 x  1
n=3
L12  6  6 x  x 2
n=1

ℓ=1

ℓ=2
L30  1
2 L13  4  x L50  1
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de

Wasserstoffatom: Radialfunktion
n=1
ℓ=0
n=2
ℓ = 0,1
n=3
| f |2
normalisierte Funktionen
f
ℓ = 0,1,2
r (a0)
r (a0)
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Wasserstoffatom: Energieschema
- log |E|
- 0.14 eV
- 0.17 eV
- 0.21 eV
- 0.28 eV
- 0.38 eV
- 0.54 eV
- 0.85 eV
- 1.5 eV
Entartung des nten Energieniveaus:
- 3.4 eV
n 1
2
 1  n 2
0
- 13.6 eV
ℓ
Orbital
0
s
1
p
2
d
3
f
4
5
6
7
8
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
9
Spin
Wie ändert sich die Wellenfunktion eines
Teilchens, wenn es um eine Achse rotiert wird?
R     ?
Volle Rotation: R  2    !
Beide Vorzeichen sind möglich,
2
2
R  2    
da nur gelten muß
Fermionen R  2   
Bosonen
R  2   
R     eis
Spin-Quantenzahl s
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de
Pauli-Prinzip
Angenommen, zwei Teilchen befinden sich im identischen Zustand.
  r1 , r2     r1    r2 
Dann ist die Wellenfunktion, bei der beide Teilchen vertauscht sind,
identisch mit der ursprünglichen Wellenfunktion.
  r1    r2     r2    r1 
Vertauschung kann aber auch durch Drehung um ein Achse
erreicht werden. Für Fermionen haben wir demnach:
  r2    r1   R   r1    r2     R  r1    R  r2     r1    r2 
Zwei Fermionen können niemals im gleichen Zustand sein!
PC II für Biochemiker
Eberhard-Karls-Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Prof. Dr. J. Enderlein, http://www.joerg-enderlein.de