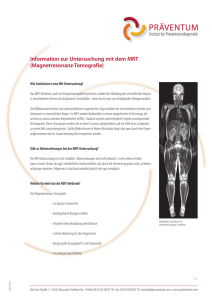
CT_MR

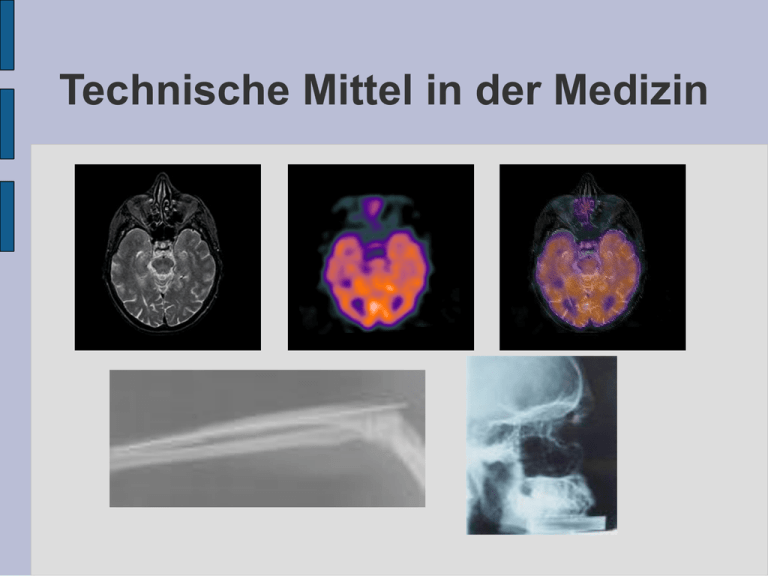
Technische Mittel in der Medizin
Technische Mittel in der Medizin




Verschiedene Verfahren und ihre Unterschiede
 Röntgen
 Ultraschall
 Magnetresonanztomographie (MRT)
 Computertomographie (CT)
Computertomographie
 Sequentielle CT
 Spiral-CT
Mathematik
 Schichtmodell
 Aufstellen eines linearen Gleichungssystems
Hersteller/ Quellen
Röntgen


Zur oberflächlichen
Untersuchung
grober Strukturen
wie z.B. Knochen
Kontrastmittelverabr
eichung in
besonderen Fällen
Ultraschall



Schallwellen KEINE Strahlung
Aufnahme von inneren Organen, Geweben,
Blutfluss und Gefäßen
Anwendungsgebiete: Bauchbereich (z.B.
Nierensteine
Schallschatten),
Bewegungsapparat, Schädel, ...
Magnetresonanztomographie (MRT)




Stellt unterschiedliche
Gewebetypen als
Bildkontrast dar
Keine Röntgenstrahlen
sondern Magnetfeld
und Radiowellen,
nichtinvasiv
Liefert
außergewöhnlich klare
Bilder
Anwendungsgebiete:
Kopf, Wirbelsäule, und
andere
Gewebestrukturen
Gesund (MRT)
Gehirntumor (MRT)
Schlaganfall (MRT)
Alzheimer (MRT)
Kreuzfeld-Jakob-Krankheit
(MRT)
Chorea Huntigton (MRT)
Computertomographie
Computertomographischer Querschnitt
einer Hirnregion
Computertomographie





schmerzfreie Untersuchungsmethode
Position des Patienten legt fest, welche
Schicht dargestellt werden soll
Sequentielle CT: Strahlenquelle Bündel
paralleler Strahlen durchqueren
Körperschicht
Strahlenempfänger misst
Stärke der Strahlung
In Bereichen mit periodischen Bewegungen
(z.B. Lunge, Herz) nur begrenzt aussagefähig
Spiral-CT: „Volumenaufnahme-Verfahren“
Röhrenstrahl tastet Körper spiralförmig ab
Aufbau eines
Computertomographen
Schichtmodell





I 0 = Intensität des Strahls vor
dem Eintritt in M
M = Materialschicht
I 1 = Intensität des Strahls
beim Austritt aus M
= Schwächungskoeffizient
Man kann davon ausgehen,
dass jeder einzelne Strahl
viele aufeinander folgende
Materialschichten gleicher
Dicke auf dem kürzesten
durchläuft
Schichtmodell II

Werden mehrere Schichten
M 1 , M 2 ,... , M n
mit den
Schwächungskoeffizienten
1 , 2 ,... , n
durchluafen, so multiplizieren
1 , 2 ,... , n
sich entsprechend
und
dieIIntensität
am Ende des
n= 1⋅ 2⋅ ...⋅ n⋅ I 0
Weges ist
Aufstellen eines linearen
Gleichungssystems

Um eine lineare Gleichung zu
erhalten, logarithmiert man
und erhält für
x1= log
1
,x2= log
2
,...,xn= log
n
x1 x2 ... xn= logdie
I n − log I 0
Beziehung

Der Querschnitt Q des
Messobjektes besteht in
diesem Fall aus 9
Bildpunkten. Hier muss man
also die Logarithmen von 9
Schwächungskoeffizienten
Aufstellen eines linearen
Gleichungssystems
Wird bei jedem Strahl s die Differenz
d = log(I n ) - log(I 0 ) aus den gemessenen
Intensitäten berechnet, so ist d in erster
Näherung gleich der Variablen, die zu den auf
dem Weg des Strahls liegenden Bildpunkte
gehören. In meinem Beispiel kann man sich auf
die Strahlen beschränken, die alle auf dem
Weg liegenden Zellen zentral treffen. Hier gibt
es also 16 Strahlen mit folgenden
dazugehörigen Differenzen aus den
Intensitäten:
Aufstellen eines linearen
Gleichungssystems
Aufstellen eines linearen
Gleichungssystems
Aus den bisherigen Erkenntnissen gelangt man
zu folgendem LGS:
Hersteller/ Quellen










Siemens
HP
LG
ATMOS Medizintechnik GmbH & Co. KG
Lambacher Schweizer Analytische
Geometrie mit linearer Algebra
www.med.harvard.com
www.medical.siemens.com
www.radiologie-sachsen.de
www.wikipedia.de
Verschiedene Fachliteratur