Vorlesung 20.07.00

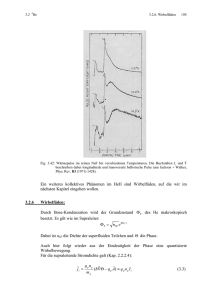
5.1.5 3He/4He Mischungskühlung 214
5.1 Kühltechniken
5.1.3
Joule-Thomson Kühler
Fig. 5.13 zeigt das Prinzip des Joule-Thomson-Effekts. Dabei strömt ein Arbeitsgas
mit hohem Druck durch einen porösen Stopfen oder eine Drossel und entspannt sich.
Fig. 5.13: Joule Thomson Effekt
Ändert das Gas dabei seine Temperatur, so spricht man vom Joule-Thomson-Effekt.
Wir betrachten die Arbeitsbilanz. Während links ein Volumen V1 im Stopfen
verschwindet, entsteht neu auf der rechten Seite das Volumen V2. Da die Drücke p1
und p2 konstant gehalten werden, gilt links:
0
0
W1 = − pdV = − p1 dV = + p1V1
V1
da p = p1 = const.
V1
und entsprechend rechts
V2
W2 = pdV = p2V2
0
Nach dem 1. Hauptsatz ist zudem:
∆U = ∆Q − ∆W
Da keine Wärme zu- oder abgeführt wird, ist ∆Q=0, (adiabatisch), so dass gilt:
U 2 − U 1 = W1 − W2 = p1V1 − p2V2
bzw.
U 2 + p 2V2 = U 1 + p1V1
D.h. die Enthalpie H ≡ U + pV bleibt beim Durchtritt durch den Stopfen ungeändert.
Dies gilt generell für alle Gase.
Nehmen wir zunächst an, das Arbeitsgas sei ein ideales Gas, d.h. die Teilchen
wechselwirken nicht miteinander. Dann enthält die innere Energie U nur die
kinetische Energie der Teilchen, und diese hängt nur von der Temperatur, aber nicht
von der Gasdichte bzw. dem Druck ab. Wegen pV=NkT hängt auch das Produkt pV
nur von der Temperatur ab, nicht aber vom Druck. Insgesamt ist also auch H nur von
T abhängig. Da sich H nicht ändert (s.o.) kann sich also auch T nicht geändert haben.
Ideale Gase zeigen also keinen Joule-Thomson-Effekt.
Wie verhält sich nun ein reales Gas? Betrachten wir dazu das pT-Diagramm für
Stickstoff (Fig. 5.14). In dieses sind die Isenthalpen eingezeichnet. Dies sind die
Kurven mit konstanter Enthalpie H, auf denen sich das Gas beim Durchgang durch
den Stopfen bewegt. Sie sind für ideale Gase horizontale Geraden, da die Temperatur
5.1 Kühltechniken
5.1.5 3He/4He Mischungskühlung 215
Fig. 5.14: pT-Diagramm für Stickstoff bzw. Helium(aus: Kent)
konstant ist. Für ein reales Gas sind sie stark gebogen und durchlaufen ein
Maximum.
Dieses Verhalten kann mit dem in Fig. 5.15 dargestellten interatomaren Potenzial
erklärt werden. Bei hohen Drücken ist der mittlere Abstand der Teilchen klein, so
dass sie sich häufig im stark abstoßenden Bereich des Potenzials befinden. Bei
Expansion laufen sie also bergab und werden beschleunigt, so dass ihre kinetische
Energie und damit die Temperatur zunimmt. Entsprechend steigt die Isenthalpe bei
abnehmendem Druck zu höherer Temperatur an.
Bei niedrigeren Drücken halten sich die Teilchen dagegen bevorzugt im anziehenden
Bereich des Potenzials auf. Dort werden sie bei Expansion verzögert. Also
abgekühlt. Entsprechend sinkt die Isenthalpe wieder ab. Das Maximum der
Isenthalpe ist die Grenze zwischen Erwärmung und Abkühlung und heißt daher
Inversionsdruck. Die Verbindungslinie aller Maxima heißt Inversionskurve. Sie ist in
fig. 5.14 gestrichelt eingezeichnet und umfaßt das schraffierte Gebiet, in dem
Abkühlung auftritt. Die höchste Temperatur, bei der gerade noch bei p=0 Abkühlung
auftritt, heißt Inversionstemperatur.
Es dürfen also nicht zu hohe Anfangs-Temperaturen und -Drücke verwendet werden.
Für Luft (N2,O2) liegt die Inversionstemperatur höher als die Zimmertemperatur, so
dass deren Verflüssigung mit Hilfe des Joule-Thomson-Effekts möglich ist. Dies
wird im Linde-Verfahren angewendet, siehe Fig. 5.16. Hier strömt das Gas erst durch
einen Gegenstromkühler und dann durch die Drossel, so dass das expandierte kalte
Gas das einströmende warme Gas vorkühlen kann. Dabei wird das Gas laufend
kälter, bis Flüssigkeit von der Düse tropft.
5.1.5 3He/4He Mischungskühlung 216
5.1 Kühltechniken
Fig. 5.15: Interatomares Potenzial im realen Gas
Fig. 5.16: Linde-Verfahren zu Verflüssigung von Luft.
5.1.4
Verdampfungskühler
Wenn wir die Windrichtung feststellen wollen, können wir einen Finger anfeuchten
und hochstrecken. Die angeströmte Seite wird kalt, da hier die Feuchtigkeit
verdunstet.
Die Abkühlung kommt daher, dass beim Übergang der Teilchen in die Gasphase
Arbeit gegen die Bindungskräfte zu den Nachbarn in der Flüssigkeit geleistet werden
muß, siehe Fig. 5.17.
Fig. 5.17: Prinzip der Verdunstung
In Fig. 5.18 ist das entsprechende Potenzial dargestellt. Die Bindungsenergie wirkt
als Potenzialschwelle zwischen Flüssigkeit und Gas. Bei endlicher Temperatur haben
die Teilchen in der Flüssigkeit eine Boltzmann-Verteilung, in der sich stets auch
5.1.5 3He/4He Mischungskühlung 217
5.1 Kühltechniken
Teilchen mit genügend hoher Energie befinden, so dass sie die Schwelle überwinden
und verdampfen können. Dabei ändert sich die Exponent der Verteilung nicht. Die
verdampften Teilchen haben also die Temperatur der Flüssigkeit. Jedoch gehen der
Flüssigkeit ständig die schnellsten Teilchen verloren, so dass sich deren
Boltzmannverteilung abkühlt. Dies erklärt die Verdampfungskühlung.
Läßt man eine Flüssigkeit unter vermindertem Druck verdampfen (durch
Abpumpen), so kühlt sie sich laufend ab. Diese Abkühlung erreicht aber eine Grenze,
wenn kBT<<EBindung wird, weil dann nur noch exponentiell wenige Teilchen die
Potenzialschwelle überwinden können. Für 4He liegt diese Grenze bei ca. 1K, bei
3
He bei 0,3K. Noch tiefere Temperaturen können durch sog. Mischkühler erreicht
werden.
Fig. 5.18: Potenzialverlauf in der Flüssigkeit bzw. im Gas
3.1.5
3
He/4He Mischungskühlung:
Zunächst betrachten wir nochmals das Phasendiagramm der 3He/4He-Mischungen
(Fig. 5.19), das in Kap. 3.4 besprochen wurde. Bei Temperaturen unter 0,87K
entmischen sich die Isotope. Bei T≈0 ist die 3He-Phase praktisch zu 100%
konzentriet, während die 4He Phase im Gleichgewicht noch 6,4% 3He enthält. Dieses
bildet (siehe Kap. 3.4) ein entartetes Fermigas mit sehr niedriger Fermi-Temperatur.
Fig. 5.19: Phasendiagramm
5.1 Kühltechniken
5.1.5 3He/4He Mischungskühlung 218
Die Wärmekapazität je Teilchen des Fermigases ist 1 π 2 k BT / TF (s. Kittel). Da die
2
Fermitemperatur TF des 3He im 4He viel niedriger ist als im konzentrierten 3He, ist
die Wärmekapazität je Atom entsprechend höher. Treten also 3He-Atome von der
konzentrierten in die verdünnte Phase über, so können sie dort sehr viel mehr Wärme
aufnehmen. Wird jedoch keine Wärme von außen zugeführt, so kühlen sich die 3HeAtome ab. Dies ist das Kühlprinzip des 3He-4He-Mischungskühlers.
Um ständig 3He-Atome vom 3He ins 4He übertreten zu lassen, ist ein kontinuierlicher
Kreislauf gemäß Fig. 5.20 nötig.
Fig. 5.20: 3He-4He-Entmischungskühler (aus: Mc Clintiock).
Von oben strömt flüssiges 3He aus einem 1K Wärmebad durch eine sogenannte
Destillationskammer nach unten. In dieser wird es auf 0,7K gekühlt. Das 3He fließt
weiter über einen Wärmetauscher in die Mischkammer (mixing chamber). Diese
enthält die beiden Phasen: 3He reich (concentrated phase) und 4He-reich (dilute
phase). Dazwischen liegt die Phasengrenze. Damit das 3He ständig durch diese
hindurchtritt, muß auf der 4He-Seite die 3He-Konzentration unter den
Gleichgewichtswert abgesenkt werden. Dies entspricht genau dem „Abpumpen“ des
Gases bei der Verdampfungskühlung, siehe 5.1.4. Die „Abpumpen“ des 3He im 4He
erfolgt über ein zweites Rohr, das über den Wärmetauscher zur Destillationskammer
führt. Diese befindet sich auf 0,7K, so dass das 3He bereits verdampfen kann und
durch ein Pumprohr abdestilliert wird, während das 4He bei dieser Temperatur
praktisch noch nicht verdampft. Durch die Destillation wird die 3He-Konzentration in
der oberen Kammer sehr niedrig gehalten, so dass das 3He im
Konzentrationsgradienten kontinuierlich von unten nach oben fließt und so die
Lösung von immer neuem 3He im 4He ermöglicht. So ergibt sich eine kontinuierliche
Abkühlung bis auf Temperaturen von ca. 10mK. Der Rekord liegt bei ca. 2mK.
Für noch tiefere Temperaturen nutzt man die magnetischen Kernmomente. Auf
dieses Prinzip wollen wir im nächsten Kapitel eingehen.
5.1 Kühltechniken
5.1.6
5.1.6 Kühlung durch magnetische Zentren 219
Kühlung durch magnetische Zentren:
Lokalisierte magnetische Momente im Festkörper können zur Kühlung verwendet
werden. Dabei kann es sich entweder um Momente der Elektronenhülle
(paramagnetische Salze) oder des Kerns (z.B. Cu-Metall) handeln. Zunächst
beschreiben wir den Kühleffekt allgemein.
Im äußeren Magnetfeld bildet der Gesamtdrehimpuls J eines magnetischen Zentrums
bekanntlich Eigenzustände zu festem Jz mit den Energieabständen:
∆E = γDB
Die Niveauabstände sind also durch das Magnetfeld abstimmbar. In kleinen Feldern,
entsprechend ∆E<<kT sind alle Niveaus gleichmäßig bevölkert, in großen Feldern
mit ∆E>>kT nur das unterste. Damit läßt sich eine Kühlvorrichtung aufbauen, die in
Fig. 5.21 schematisch dargestellt ist.
Fig. 5.21 Kühlvorrichtung
Die Probe befindet sich thermisch isoliert im Vakuum in einem supraleitenden
Magneten. Sie ist über einen „Wärmeschalter“ mit einem Wärmebad verbunden. Der
Wärmeschalter ist meist ein Al-Draht, der durch eine kleine Magnetspule
normalleitend geschaltet wird und dann hohe Wärmeleitfähigkeit besitzt, während er
im supraleitenden Zustand bei tiefer Temperatur die Wärme sehr schlecht leitet.
Anfangs ist der Wärmeschalter geschlossen. Dann ist die Probe bei der Temperatur
T0. Nun wird der SL Magnet hochgefahren, bis ∆E>>kBT0 ist. Dabei entvölkern sich
alle höheren Niveaus. Sie geben ihre Energie entweder ans Gitter (Salze) oder an die
Leitungselektronen (Metalle) ab. Über den Wärmeschalter fließt die Energie ins
Wärmebad.
Nach einiger Zeit sind alle magnetischen Zentren im Grundzustand. Dann wird der
Wärmeschalter geöffnet, und das Magnetfeld der Probe langsam wieder abgesenkt.
Dies kann Stunden bzw. Tage dauern, denn die Zentren müssen stets mit der Probe
im Gleichgewicht bleiben, um irreversible Prozesse zu vermeiden. Durch die
Absenkung des Magnetfeldes kommt die Probe in den Bereich ∆E≈kBT, so dass die
höheren Niveaus langsam wieder bevölkert werden und dabei Energie aufnehmen.
Die Energie wird jetzt wieder dem Gitter bzw. den Leitungselektronen entzogen.
Dadurch kühlt die Probe ab. Soll bei konstanter Temperatur eine Messung
vorgenommen werden, wird das Magnetfeld so lange angehalten. Bei B=0 ist die
tiefste Temperatur erreicht.
Im Prinzip müßten sich auf diese Weise beliebig tiefe Temperaturen erreiche lassen.
Eine Grenze wird aber durch die Wechselwirkung der magnetischen Zentren
5.1 Kühltechniken
5.1.6 Kühlung durch magnetische Zentren 220
untereinander gesetzt. Diese richtet ihrerseits die magnetischen Momente aus und
verhindert so, dass sich diese in schwachen Magnetfeldern (entsprechend kleinen
Temperaturen) noch nach den äußeren Feldern ausrichten können. Diese Grenze liegt
für magnetische Salze (z.B. Cer-magnesium-Nitrat, CMN) bei ca. 10mK. Da dieser
Temperaturbereich heutzutage durch Mischkühler leichter erreichbar ist, werden die
Salze nicht mehr verwendet. Weit tiefere Temperaturen kann man jedoch durch
Verwendung von Kernspins erreichen. Diese haben viel kleinere Momente, so dass
sie nur bei sehr tiefen Temperaturen (<10mK) verwendet werden können. Da aber
die Wechselwirkung der Kernspins untereinander ebenfalls verschwindend gering ist,
können damit Temperaturen bis herab zu ca. 50µK erreicht werden. Dies sind die
tiefsten bisher erreichten Gittertemperaturen in Festkörpern.
Fig. 5.22 zeigt eine detailliertere Skizze eines 1-stufigen Kernentmagnetisierungskühlers in üblicher Bauform.
Fig. 5.22: Einstufige Kernspinentmagnetisierungsmaschine