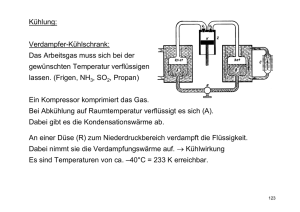
Vorlesung 25.05.00

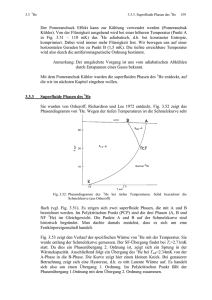
3.2 4He
3.2.6. Wirbelfäden
150
Fig. 3.42: Wärmepulse im reinen NaF bei verschiedenen Temperaturen. Die Buchstaben L und T
beschreiben dabei longitudinale und transversale ballistische Pulse (aus Jackson + Walker,
Phys. Rev. B3 (1971) 1428).
Ein weiteres kollektives Phänomen im HeII sind Wirbelfäden, auf die wir im
nächsten Kapitel eingehen wollen.
3.2.6
Wirbelfäden:
Durch Bose-Kondensation wird der Grundzustand Φ 0 des He makroskopisch
besetzt. Es gilt wie im Supraleiter:
Φ 0 = nSF e iΘ ( r )
Dabei ist nSF die Dichte der superfluiden Teilchen und Θ die Phase.
Auch hier folgt wieder aus der Eindeutigkeit der Phase eine quantisierte
Wirbelbewegung.
Für die supraleitende Stromdichte galt (Kap. 2.2.2.4):
H
H q pnp H
H
(D∇Θ − q p A) ≡ q p n p vs
js =
mp
(3.3)
3.2 4He
3.2.6. Wirbelfäden
151
Im Gegensatz zum Supraleiter ist He nicht geladen (q=0). Daher gibt es keinen
Magnetfluß und der Term qA verschwindet. Außerdem muß anstelle der
Ladungstromdichte js die superfluide Geschwindigkeit verwendet werden. Für diese
ergibt sich aus (3.3):
H
D H
∇Θ
vSF =
mHe
Entsprechend der Flußquantisierung im SL benutzen wir dieses Ergebnis zur
Wirbelquantisierung. Dazu bilden wir das Integral über einen geschlossenen Weg:
H H
H H
D H H
D
Γ ≡ vSF dr =
∇Θdr =
∇Θdr
mHe
mHe
Γ ist die aus der Strömungsmechanik bekannte Zirkulation.
Wie in Kap. 2.2.3.7 beschrieben, darf sich der Phasenfaktor eiΘ bei einem
geschlossenen Umlauf nicht ändern. Daher muß gelten:
H H
∇Θdr = 2πn,
n = ganze Zahl
h
quantisiert:
mHe
h
Γ=
n
mHe
Die Zirkulation ist also mit der Größe
(3.4)
Anmerkung: Auch in der klassischen Strömungslehre ist die Zirkulation
Γ = const. , unabhängig vom Integrationsweg (Thomsonscher
Satz). Jedoch ist hier die Konstante zusätzlich quantisiert.
Beim SL erhielten wir je nach Tiefe des Integrationsweges entweder die
Fluxoidquantisierung oder die Flußquantisierung (Kap. 2.2.2.4). Hier ergibt sich, da
keine Ladungen vorhanden sind, immer die gleiche Quantisierung – unabhängig von
der Tiefe des Integrationsweges.
Wir wollen dies nun auf einen einzelnen Wirbel anwenden (s. Fig. 3.43).
Fig. 3.43: Wirbel im Helium.
Das Helium fließt superfluid
im Kreis.
Das Problem ist zylindersymmetrisch. Aus diesem Grund wählen wir einen Kreis mit
Radius r als Integrationsweg. Auf diesem ist die Geschwindigkeit konstant. Damit
folgt für die Zirkulation:
Γ = v dr = v 2πr
v=
Γ
1 1
= n ∝
2πr m r r
3.2 4He
3.2.6. Wirbelfäden
152
Im Gegensatz zum SL, wo die Abschirmströme um einen Flußfaden nach außen
exponentiell ( ∝ e − r / λL ) abklingen, klingt hier das Strömungsfeld nur mit 1/r ab.
Damit hat die Wechselwirkung zwischen den Wirbelfäden im He eine unendlich
große Reichweite. In der Mitte hat das Strömungsfeld theoretisch eine Singularität.
Sie ist aber auf der Skala der Atomabstände abgeschnitten, weil dann die
Kontinuumsmechanik nicht mehr gültig ist.
Wir wollen nun überlegen, welche Energie mindestens nötig ist, um einen Wirbel zu
erzeugen. Nach (3.4) ergibt n=1 das kleinste Γ≠0 und damit die niedrigste kinetische
Energie.
Je länger ein Wirbelfaden ist, desto mehr Teilchen müssen in Bewegung gesetzt
werden. Um eine kleine Anregungsenergie zu erhalten, muß der Faden also
möglichst kurz sein. Wegen Γ=const. kann der Wirbelfaden nicht plötzlich aufhören,
sondern er muß entweder von Wand zu Wand laufen oder ringförmig geschlossen
sein. Der minimale Durchmesser eines solchen Rings beträgt einige Atomabstände.
Landau hatte vermutet, daß die Rotonen solche Wirbelringe seien, und hatte ihnen
deshalb diesen Namen gegeben. Da sich die Rotonen aber durch Neutronenstreuung
nachweisen lassen, weiß man heute, daß es sich dabei nicht um Wirbel sondern um
Dichteschwankungen handelt. Die Wirbel haben höhere Anregungsenergie, auch die
kleinsten. Daher sind sie thermisch nicht angeregt.
Da Wirbel nur stabil sind, wenn sie sich entlang ihrer Mittelachse bewegen (das
kennen wir von Rauchringen!), haben sie nicht nur Energie, sondern auch Impuls.
ε
ω
bzw.
kleiner als für Rotonen
Der Impuls ist dabei so groß, daß das Verhältnis
p
k
ist. Entsprechend sind sie bei niedrigeren Geschwindigkeiten anregbar. Daher ist die
gemessene kritische Geschwindigkeit von HeII in Kapillaren stets kleiner als die
Landausche kritische Geschwindigkeit. Beim Überschreiten werden Wirbel erzeugt.
Wie können solche Wirbelfäden sichtbar gemacht werden? Dazu rotiert man den
gesamten Kryostaten und kühlt das He während der Drehung unter den Lambda
Punkt ab.
Ist die Rotation sehr langsam, enthält die Flüssigkeit nur wenig kinetische Energie,
die nicht ausreicht, einen Wirbelfaden zu erzeugen. Da die Zirkulation null ist, ist
auch der Drehimpuls L=0. Das He bleibt also bei unterschreiten von Tλ plötzlich
stehen und erzeugt einen meßbaren Rückstoß auf die Gefäßwand. Dieser wirbelfreie
Zustand ist vergleichbar mit dem Meissner Zustand des SL.
Ist die Rotation schneller, bilden sich beim Abkühlen unter Tλ wie im SL 2. Art
(Shubnikov-Phase) Wirbel (s. Fig. 3.44a). Es zeigt sich ein charakteristisches Muster
von Wirbelfäden (s. Fig. 3.44b). Da die Fäden makroskopisch lang sind und ihre
Zirkulation nicht abklingt, muß sich das gesamte He drehen. Dies ist mit viel
Energie verbunden, so dass nur wenig Wirbel angeregt werden.
Fig. 3.44 zeigt eine Methode Wirbelfäden sichtbar zu machen. Dazu wir die HeOberfläche mit Elektronen aus einer Kathode besprüht. Diese fangen sich im
Wirbelkern. Durch Anlegen eines elektrischen Feld (200V) parallel zur
Rotationsachse werden die Elektronen aus den Wirbelfäden herausgezogen. Mittels
eines Leuchtschirms, der senkrecht zur Rotationsachse oberhalb des He angebracht
ist, kann so der Ort der Elektronen und damit der Ort der Wirbelfäden sichtbar
gemacht werden.
3.2 4He
3.2.6. Wirbelfäden
153
Fig. 3.44: Experimentelle Beobachtung der Wirbelfäden (aus McClintock usw.)
Das experimentell beobachtete Wirbelmuster ist in Fig. 3.45 abgebildet. Der
Gefäßdurchmesser beträgt ca. 2 mm. Die Rotationsgeschwindigkeit wurde zwischen
0,3 rad/s (a) und 0,9 rad/s (l) variiert. Die stabilen Muster drehen sich dabei mit dem
Gefäß mit.
Fig. 3.45: Stabile Wirbel Muster im rotierenden Helium (aus McClintock usw.)
Ein weiteres Isotop des Heliums ist das 3He, auf das wir im nächsten Kapitel
eingehen wollen.
3.3 3He
3.3.
3.3.1. 3He als Normalflüssigkeit
3
154
He
Für 3He gilt die Fermistatistik. Die Fermi-Eigenschaften zeigen sich besonders in
dichten Gasen, also hier in der 3He-Flüssigkeit.
3.3.1
3
He als Normalflüssigkeit
Die Fermistatistik kennen wir von den Elektronen im Festkörper. Es gilt für die
Besetzungswahrscheinlichkeit:
1
f (ε ) = E −µ (T )
e
k BT
+1
Dabei ist:
µ(T) das chemische Potenzial für N=const. bzw.
µ(0)≡εF die Fermienergie.
Die für T=0 definierte Fermitemperatur ist gegeben mit:
ε
TF ≡ F
kB
Dabei gilt für:
T >> TF:
T << TF:
das chemische Potenzial sinkt, da die Zustandsdichte für große Energien
zunimmt. Für µ→0 erhalten wir ein Boltzmann-Gas (s.
Festkörperphysik).
wir erhalten ein entartetes Fermigas mit scharfer Fermikante.
Wie groß ist die Fermitemperatur im 3He?
Nach Kap. 6 Kittel ist die Fermitemperatur gegeben durch:
2/3
D 2 æ 3π 2 N ö
ç
(3.4)
TF =
2mk B çè V
Die Masse m ist hier die Masse des Heliums. Sie ist viel größer als die Masse des
Elektrons. Damit ist TF,He << TF,Elektronen im Festkörper.
Nach (3.4) ergibt sich eine Fermitemperatur für He von TF≈5K.
Sie kann durch Messen der spezifischen Wärme bestimmt werden (Fig. 3.46). Diese
ist für 3He bei hohen Temperaturen (T>2K) vergleichbar mit der von 4He. Bis ca.
1K zeigt sich eine Abnahme wie im klassischen Gas. Erst bei sehr niedrigen
Temperaturen (T<100mK) ergibt sich eine lineare Temperaturabhängigkeit (c∝T).
Dieses Verhalten kennen wir bereits vom entarteten Fermigas der Elektronen im
Festkörper.
Fittet man den genauen Verlauf an, erhält man eine Fermitemperatur von TF≈0,5K.
Dieser Wert beträgt nur 10% des eigentlich erwarteten Wertes. Der Grund für diese
Diskrepanz liegt in einer vergrößerten effektiven Masse m3* aufgrund der Wechselwirkung der Teilchen. Schematisch ist dies in Fig. 3.47 gezeigt. Das grau markierte
Teilchen kann sich schlecht unabhängig von den anderen bewegen. Diese müssen
ihm „aus dem Weg gehen“ und erzeugen damit eine Rückströmung (back-flow). Es
muß also nicht nur eine, sondern mehrere Massen beschleunigt werden. Wir können
3.3 3He
3.3.1. 3He als Normalflüssigkeit
155
Fig. 3.46: Spezifische Wärmekapazität von 3He in Abhängigkeit von der Temperatur (aus Kent)
Fig. 3.47: Schematische Darstellung der Rückströmung aufgrund der Bewegung eines Teilchens
ein Quasiteilchen bestehend aus dem einen (grauen) Teilchen und den
rückströmenden Teilchen mit einer gesamten effektiven Masse m* definieren.
Aufgrund dieser vergrößerten Masse ist die Fermitemperatur verkleinert. Für die
Theorie der Quasiteilchen im flüssigen 3He hat Landau die Theorie der
Fermiflüssigkeit entwickelt. (Vergleiche dazu Kap. 10 Kittel).
3
He ist also bei tiefen Temperaturen eine entartete Fermiflüssigkeit.
Eine weitere wichtige Eigenschaft des 3He ist, sein unkompensiertes Kernmagnetisches Moment und der daraus resultierende schwache Magnetismus.
Fig. 3.48 zeigt die magnetische Suszeptibilität des 3He. Aufgetragen ist das Produkt
aus Suszeptibilität χ und Temperatur T als Funktion von der Temperatur. Für hohe
Temperaturen ist diese Produkt konstant, d.h. χ ∝ 1 (Curie-Gesetz). Bei tiefen
T
Temperaturen ist χT ∝ T , also χ = const. , wobei χ viel kleiner als im Curie-Gesetz
ist. Eine solche Konstanz erwartet man für ein entartetes Fermigas mit Paulischem
Spin-Paramagnetismus. Diesen wiederholen wir kurz aus der Festkörperphysik, siehe
Fig. 3.49. Dort ist in (a) die Energie gegenüber der Zustandsdichte aufgetragen, und
zwar für beide Spinsorten, deren Anzahl gleich ist. (b) zeigt die Situation nach dem
Einschalten eines Feldes B≠0. Die Energien werden je nach Spinstellung um die
magnetische Dipolenergie abgesenkt bzw. angehoben. (c) zeigt die Reaktion: die
Fermienergie gleicht sich aus, d.h. die Anzahl beider Spinsorten wird
unterschiedlich:
∆N = 2µ N BD(ε F )
3.3 3He
3.3.1. 3He als Normalflüssigkeit
156
Fig. 3.48: Magnetische Suszeptibilität von 3He als Funktion der Temperatur aufgetragen (aus Kent)
Fig. 3.49: Schematische Darstellung des Pauli-Spinmagnetismus
Für die Suszeptibilität gilt:
∆N
= 2 µ 0 µ N2 D (ε F )
B
Dies ist die von der Temperatur unabhängige Paulische Spinsuszeptibilität des
entarteten Fermigases bzw. des 3He bei tiefen Temperaturen.
χ = µ0 µ N
Die magnetischen Eigenschaften haben auch einen Einfluß auf die feste Phase, auf
die wir im nächsten Kapitel eingehen wollen.
3.3 3He
3.3.2.
3.3.2. festes 3He und Pomeranchuk Effekt
157
festes 3He und Pomeranchuk Effekt
Betrachten wir dazu das Phasendiagramm flüssig/fest von 3He und 4He (Fig. 3.50).
(Die Temperatur ist in dieser Figur logarithmisch aufgetragen.)
Das 4He liegt meist in der hcp-Kristallstruktur vor. Es zeigt sich ein „Zwickel“ mit
einer bcc-Struktur. An diesem mündet die λ-Linie ein (nicht eingezeichnet). Bei
hohen Temperaturen ist die Kristallstruktur fcc. Für tiefe Temperaturen (T<1K) zeigt
sich ein flacher Verlauf der Schmelzkurve.
3
He liegt ebenfalls als fcc-Struktur bei hohen Temperaturen vor. Es zeigt einen bcchcp-Übergang bei 100 bar Druck und tiefen Temperaturen. Bei T=0,32 ist ein
Minimum, d.h. ein Wiederanstieg der Schmelzkurve für kleinere Temperaturen, zu
verzeichnen. Dies ist der „Pomeranchuk-Effekt“.
Fig. 3.50: Phasendiagramm flüssig/fest für 3He und 4He (aus Bennemann und Kettersion, Teil I)
Wie kann dieses Minimum erklärt werden? Allgemein beschreibt man
thermodynamische Phasengrenzkurven mit der Clausius-Clapeyron-Gleichung:
dp
dT
=
Schmelzkurve
S flüssig − S fest
V flüssig − V fest
mit ∆S =
QSchmelz
TSchmelz
Diese beschreibt die Steigung der Schmelzkurve im p-T-Diagramm. Da das Volumen
bei der Verfestigung abnimmt, bedeutet die negative Steigung unterhalb des
Minimums, daß die Entropie zunimmt, also Sfest > Sflüssigt ist! Demnach ist die
Flüssigkeit geordneter als der Festkörper. Die Ursache liegt in den magnetischen
Eigenschaften des 3He. Im festen He sind die Atome halbwegs lokalisiert, d.h. die
Kernspins der einzelnen Atome wechselwirken nur schwach miteinander und können
sich so unabhängig voneinander einstellen.
3.3 3He
3.3.2. festes 3He und Pomeranchuk Effekt
158
Für je zwei Spineinstellungen wird daher die Entropie:
S = Nk B ln 2
unabhängig von der Temperatur für festes 3He. Damit ergibt sich bei tiefen
Temperaturen eine beträchtliche Entropie.
In der Flüssigkeit gilt die Fermistatistik. Wie wir sahen, ist die Wärmekapazität
proportional zur Temperatur:
C=
Damit ist
∂Q
dS
=T
∝T
∂T
dT
dS
konstant und S∝T. Die Entropie nimmt also linear mit der Temperatur
dT
ab. D.h. für tiefe Temperaturen geht im flüssigen Zustand S→0 und ist kleiner als die
temperaturunabhängige Entropie des Festkörpers.
Im oberen Teilbild von Fig. 3.51 ist die Schmelzkurve von 3He gezeigt, im unteren
Teilbild die Entropie als Funktion der Temperatur. Im Minimum der Schmelzkurve
schneidet die Linie der Entropie des Festkörpers die der Flüssigkeit (unteres Bild).
dp
Hier ist ∆S=0 und damit
= 0 ≡ Minimum. Bei sehr tiefen Temperaturen, T<2mK
dT
nimmt schließlich auch die Entropie des festen 3He ab, da es antiferromagnetisch
ordnet. Damit ist der 3. Hauptsatz erfüllt.
Fig. 3.51: Schmelzkurve und Entropie im flüssigen bzw. festen Zustand des 3He (aus Kent)
3.3 3He
3.3.3. Superfluide Phasen des 3He
159
Der Pomeranchuck Effekt kann zur Kühlung verwendet werden (Pomeranchuk
Kühler). Von der Flüssigkeit ausgehend wird bei einer höheren Temperatur (Punkt A
in Fig. 3.51 – 110 mK) das 3He adiabatisch, d.h. bei konstanter Entropie,
komprimiert. Dabei wird immer mehr Flüssigkeit fest. Wir bewegen uns auf einer
horizontalen Geraden bis zu Punkt B (1,5 mK). Die tiefste erreichbare Temperatur
wird also durch die antiferromagnetische Ordnung bestimmt.
Anmerkung: Der umgekehrte Vorgang ist uns vom adiabatischen Abkühlen
durch Entspannen eines Gases bekannt.
Mit dem Pomeranchuk Kühler wurden die superfluiden Phasen des 3He entdeckt, auf
die wir im nächsten Kapitel eingehen wollen.
3.3.3
Superfluide Phasen des 3He
Sie wurden von Osheroff, Richardson und Lee 1972 entdeckt. Fig. 3.52 zeigt das
Phasendiagramm von 3He. Wegen der tiefen Temperaturen ist die Schmelzkurve sehr
Fig. 3.52: Phasendiagramm des 3He bei tiefen Temperaturen. Solid bezeichnet die
Schmelzkurve (aus Osheroff)
flach (vgl. Fig. 3.51). Es zeigen sich zwei superfluide Phasen die mit A und B
bezeichnet werden. Die Punkte A und B auf der Schmelzkurve sind historisch
begründet. Man dachte damals zunächst, dass es sich um eine Festkörpereigenschaft
handelt.
Äquivalent zur Supraleitung, wo zwei Fermionen (Elektronen) ein Cooper-Paar
bilden, paaren sich hier die 3He Atome. Dabei stellen sich jedoch die Spins parallel.
Anders als im SL ist also die Spin-Wellenfunktion symmetrisch und damit nach
Pauli die Ortswellenfunktion antisymmetrisch, also L ungerade. Aus den
Experimenten zeigt sich eindeutig, daß L=1 ist, d.h. wir haben p-Wellen-Paarung.
Wegen der Parllelstellung der Spins hat jedes Paar ein magnetisches Moment. Daher
hängt das Phasendiagramm des SF 3He empfindlich vom Magnetfeld ab:
Für B>0 tritt an der Grenze zur normafluiden Phase noch eine zusätzliche A1-Phase
auf, und für B>0,6 T verschwindet die B-Phase ganz.