1. Komplexe Zahlen

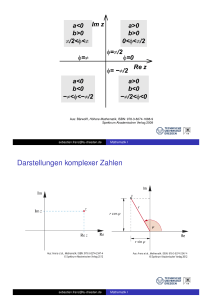
Prof. Dr. T. Nattermann
Dr. A. Blazhev
10. Übungsblatt zum Vorkurs Physik
Wintersemester 2014/15
www.ikp.uni-koeln.de/∼blazhev/vorkurs1415
1. Komplexe Zahlen
a) Wie lauten der Realteil Re(z) und der Imaginärteil Im(z) der folgenden komplexen Zahlen?
i)
3 + 5ı
iv)
(3 + 2ı)2
ii)
6 + 9ı
12
iii)
(4 + 2ı) · (3 − ı)
v)
(2 + 2ı)2 + (2 − 2ı)2
vi)
3
4 + 6ı
b) Zeigen Sie, dass Real- und Imaginärteil einer komplexen Zahl z allgemein wie folgt erhalten
werden können:
z + z∗
z − z∗
Re(z) =
Im(z) =
2
2ı
c) Nun betrachten wir zwei komplexe Zahlen zk = xk + ıyk mit k = 1, 2. Zeigen Sie, dass gilt:
i)
(z1 · z2 )∗ = z1∗ · z2∗
ii)
(z1 /z2 )∗ = z1∗ /z2∗
iii) |z1 · z2 | = |z1 | · |z2 |
d) Eine komplexe Zahl z kann sowohl in kartesischer Form mit z = x + ıy als auch in Polarform
mit z = r eıφ dargestellt werden. Zeigen Sie, dass für die Umrechnung von kartesischer Form
in Polarform gilt (solange x > 0):
y
p
r = x2 + y 2
φ = arctan
x
e) Wie lautet die Umrechnung von Polarform in kartesische Form?
f ) Berechnen Sie:
i)
√
−4
ii)
√
3 + 4ı
g) Finden Sie alle Lösungen für
x3 = −8
und geben Sie diese in kartesischer Form und Polarform an.
iii)
√
5
−1
2. Trigonometrische Funktionen
a) Zeigen Sie ausgehend von den Definitionen der trigonometrischen Funktionen und deren
Exponentialdarstellungen cos(x) = 12 (eıx + e−ıx ) und sin(x) = 21 (eıx − e−ıx ) dass gilt:
i) cos2 (x) + sin2 (x) = 1
1
1 + tan2 (x)
ii) cos2 (x) =
iii) sin2 (x) =
1
1 + cot2 (x)
b) Zeigen Sie mit Hilfe der Exponentialdarstellungen von Sinus und Kosinus und den bereits
bekannten Relationen die folgenden Additionstheoreme:
i)
cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y)
ii)
sin(2x) = 2 sin(x) cos(x)
x+y
x+y
sin(x) + sin(y) = 2 sin
cos
2
2
iii)
3. Hyperbolische Funktionen
Analog zu den Exponentialfunktion der trigonometrischen Funktionen lassen sich die sogenannten hyperbolischen Funktionen definieren als
1
cosh(x) = (ex + e−x )
2
1
sinh(x) = (ex − e−x )
2
und
Zeigen Sie mit Hilfe der Definitionen die folgenden Beziehungen:
i)
sinh(−x) = − sinh(x)
ii)
cosh2 (x) − sinh2 (x) = 1
iii)
sinh(x ± y) = sinh(x) cosh(y) ± sinh(y) cosh(x)
iv)
cosh(x ± y) = cosh(x) cosh(y) ± sinh(x) sinh(y)
und
cosh(−x) = cosh(x)
4. Ableitungen elementarer Funktionen
Berechnen Sie die Ableitungen nach x der folgenden Funktionen:
a) x2 ln(x)
e) sin(x) cos(x)
x2 + 3
x−5
x sin(x)
f) e
b)
c)
√
x+
g) ax
2
√
n
x
d)
p
3x2 + 2x − 1
h) cosh(x)