- dieter

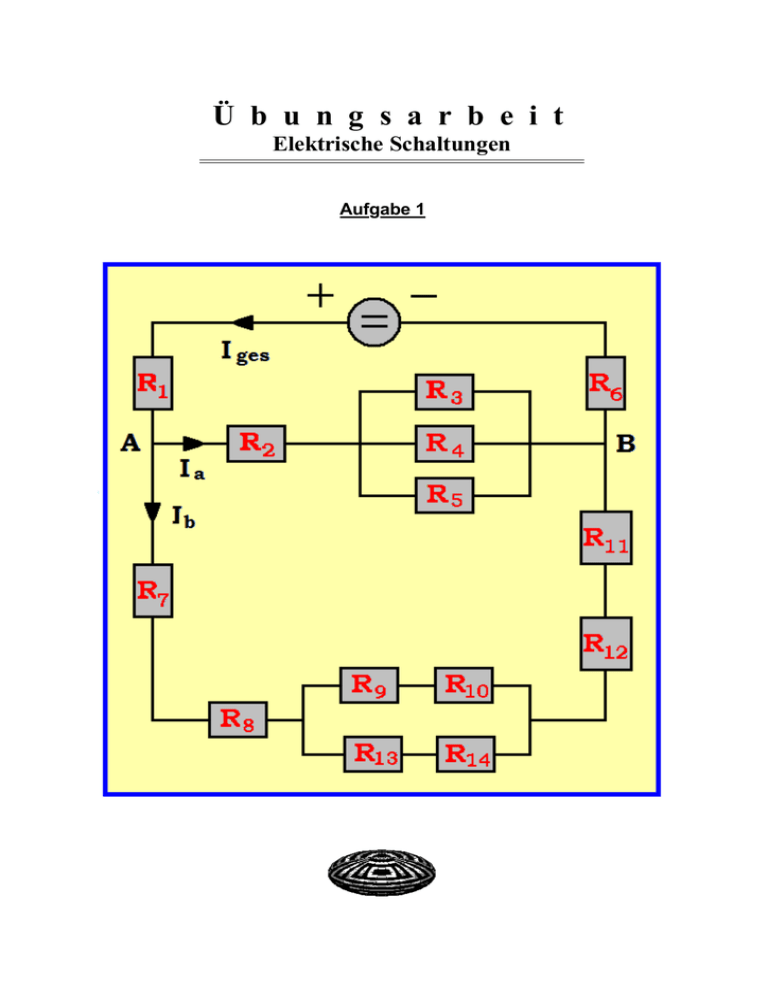
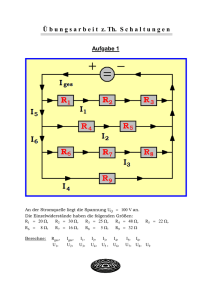
Ü b u n g s a r b e i t
Elektrische Schaltungen
Aufgabe 1
Fortsetzung von Aufgabe 1
An der Stromquelle liegt die Gesamtspannung Uges = 220 V an.
Die einzelnen Widerstände der Schaltung haben folgende Größen:
R1 = 11 Ω,
R2 = 14 Ω,
R 3 = 40 Ω,
R 4 = 60 Ω,
R 5 = 48 Ω,
R 6 = 19 Ω,
R 7 = 32 Ω,
R 8 = 46 Ω,
R 9 = 25 Ω,
R10 = 55 Ω,
R11 = 20 Ω,
R12 = 12 Ω,
R13 = 50 Ω,
R14 = 30 Ω.
Berechne: Rges,
Iges,
Ia,
Ib,
U1,
UAB, U12,
U6,
U14.
Wähle zur Berechnung dieser Größen eine sinnvolle Reihenfolge.
Aufgabe 2
Die Widerstände R1 = 20 Ω, R2 = 40 Ω, R3 = 60 Ω und R4 = 180 Ω sollen so
geschaltet werden, dass man folgende Gesamtwiderstände erhält:
a) Rges = 224 Ω
b) Rges = 118 Ω
c) Rges = 42 Ω
d) Rges = 48 Ω
Fertige zu jeder Teilaufgabe eine Schaltskizze der Widerstände an und
berechne dann jeweils den Gesamtwiderstand.
Aufgabe 3
Das Messwerk eines Drehspulinstruments trägt die Aufschrift: 400 µA, 80 mV
a) Berechne den Messwerkwiderstand RM des Drehspulinstruments.
Mit diesem Gerät soll bei Zeigervollausschlag
b) die Stromstärke 5 A c) die Spannung 250 V gemessen werden.
Berechne die Größe der Widerstände, die zum Messwerk hinzugeschaltet
werden und gib jeweils an, ob es sich dabei um eine Parallel- oder um eine
Serienschaltung handelt.
Bestimme außerdem den Gesamtwiderstand des Messgerätes, wenn es
als Amperemeter- und wenn es als Voltmeter betrieben wird.
Um wieviel Prozent weicht der Gesamtwiderstand des Voltmeters von dem
zum Messwerk hinzugeschalteten Widerstand ab ?
Aufgabe 4
Der Kupferdraht einer Spule hat die Querschnittsfläche A = 0,25 mm2 .
Der mittlere Windungsradius der Spule beträgt r = 8 cm.
Die Spule hat den Widerstand R = 150 Ω.
Ω mm 2
Der spezifische Widerstand von Kupfer ist ρCu = 0,017
.
m
Berechne die Windungszahl der Spule. Runde auf volle Windungen.
L ö s u n g e n
zu Aufgabe 1
Berechnung des Gesamtwiderstandes
Zusammenfassung der in Serie geschalteten Widerstände
R1,6
=
R1 + R6
=
11 Ω + 19 Ω
=
30 Ω
R7,8,11,12
=
R7 + R8 + R11 + R12
=
32 Ω + 46 Ω + 20 Ω + 12 Ω =
110 Ω
R9,10
=
R9 + R10
=
25 Ω + 55 Ω
=
80 Ω
R13,14
=
R13 + R14
=
50 Ω + 30 Ω
=
80 Ω
Zusammenfassung der parallel geschalteten Widerstände
bzw. Ersatzwiderstände

 −1
 1
1
1 
1
1  −1
1

R3,4,5
=
= 
=
+
+
+
+

 R3
R4
R5 
60 Ω
48 Ω 
40 Ω



R9,10,13,14
=
R9,10 ⋅ R13,14
R9,10 + R13,14
80 Ω ⋅ 80 Ω
80 Ω + 80 Ω
=

 −1
1


 0,0625 Ω 
=
16 Ω
=
40 Ω
Zusammenfassung der in Serie geschalteten Ersatzwiderstände
R2,3,4,5
=
R2 + R3,4,5
=
14 Ω + 16 Ω
=
30 Ω
R7,8,9,10,11,12,13,14
=
R7,8,11,12 + R9,10,13,14
=
110 Ω + 40 Ω
=
150 Ω
:=
Rx
:=
Ry
Zusammenfassung der parallel geschalteten Ersatzwiderstände
R2,3,4,5,x
=
R2,3,4,5 ⋅ Rx
R2,3,4,5 + Rx
=
30 Ω ⋅ 150 Ω
30 Ω + 150 Ω
=
25 Ω
Zusammenfassung der in Serie geschalteten Ersatzwiderstände
Rges
=
R1,6 + Ry
=
30 Ω + 25 Ω
Die Schaltung hat den Gesamtwiderstand Rges = 55 Ω .
=
55 Ω
Fortsetzung von Aufgabe 1
Uges
220 V
=
= 4A
Rges
55 Ω
Die Gesamtstromstärke beträgt Iges = 4 A.
Iges =
U1 = R1 ⋅ Iges = 11 Ω ⋅ 4 A = 44 V
Am Widerstand R1 liegt die Spannung U1 = 44 V.
U6 = R6 ⋅ Iges = 19 Ω ⋅ 4 A = 76 V
Am Widerstand R6 liegt die Spannung U6 = 76 V.
UAB = Uges − U1 − U6 = 220 V − 44 V − 76 V = 100 V
Zwischen Den Punkten A und B liegt die Spannung
Ia =
UAB = 100 V.
UAB
100 V
1
=
= 3 A
R2,3,4,5
3
30 Ω
Die Stromstärke Ia beträgt Ia = 3
1
A.
3
1
2
A =
A
3
3
2
A.
Die Stromstärke Ib beträgt Ib =
3
Ib = Iges − Ia = 4 A − 3
2
A = 8V
3
liegt die Spannung U12 = 8V.
U12 = R12 ⋅ Ib = 12 Ω ⋅
Am Widerstand R12
2
A hinter dem
3
1
1
A und I13,14 =
A.
=
3
3
Da R9,10 = R13,14 = 80 Ω gilt, teilt sich die Stromstärke Ib =
Widerstand R8 in zwei gleich große Teilströme I9,10
Folglich gilt für die Spannung U14:
1
U14 = R14 ⋅ I13,14 = 30 Ω ⋅ A = 10 V
3
Am Widerstand R14 liegt die Spannung U14 = 10 V.
Aufgabe 2 a
Rges = R1 +
R2 ⋅ R3
40 Ω ⋅ 60 Ω
+ R4 = 20 Ω +
+ 180 Ω = 224 Ω
R2 + R3
40 Ω + 60 Ω
Die Schaltung hat den Gesamtwiderstand Rges = 224 Ω.
Aufgabe 2 b
Rges =
R1 ⋅ R4
20 Ω ⋅ 180 Ω
= 40 Ω +
+ 60 Ω = 118 Ω
R1 + R4
20 Ω + 180 Ω
Die Schaltung hat den Gesamtwiderstand Rges = 118 Ω.
Aufgabe 2 c
Rges =
R1 ⋅ R4
R1 + R4
+
R2 ⋅ R3
R2 + R3
=
20 Ω ⋅ 180 Ω
40 Ω ⋅ 60 Ω
+
= 42 Ω
20 Ω + 180 Ω
40 Ω + 60 Ω
Die Schaltung hat den Gesamtwiderstand Rges = 42 Ω.
Aufgabe 2 d
Rges
R + R  ⋅ R + R 
20 Ω + 40 Ω  ⋅ 60 Ω + 180 Ω 
2  3
4
 1

 

=
=
R1 + R2 + R3 + R4
20 Ω + 40 Ω + 60 Ω + 180 Ω
=
60 Ω ⋅ 240 Ω
300 Ω
=
14400 Ω 2
300 Ω
=
48 Ω
Die Schaltung hat den Gesamtwiderstand Rges = 48 Ω.
Aufgabe 3 a
RM =
UM
IM
=
80 mV
400 µ A
=
0,08 V
0,0004 A
= 200 Ω
Das Messwerk des Drehspulinstruments hat den Widerstand RM = 200 Ω.
Aufgabe 3 b
Zum Messwerk muss der Widerstand RP parallel geschaltet werden.
Die Größe von RP ist so zu wählen, dass durch RP ein Strom der Stärke
IP = I − IM = 5 A − 0,0004 A = 4,9996 A hindurchfließt. Es gilt:
IM
RP
=
⇔
IP
RM
IM
0,0004 A
200
RP =
⋅ RM =
⋅ 200 Ω =
Ω ≈ 0,016 Ω
IP
4,9996 A
12499
Zum Messwerk wird der Widerstand RP = 0,016 Ω p a r a l l e l geschaltet.
Berechnung des Gesamtwiderstandes Rges des Amperemeters
200
200 Ω ⋅ 12499
Ω
RM ⋅ RP
Rges =
=
= 0,0016 Ω
200
RM + RP
200 Ω + 12499
Ω
Da der parallel geschaltete Widerstand RP sehr viel kleiner ist als der Messwerkwiderstand RM, ist der Gesamtwiderstand des Amperemeters Rges mit dem
Widerstand RP praktisch identisch.
Das Amperemeter hat den Gesamtwidwiderstand Rges = 0,016 Ω.
Aufgabe 3 c
US
=
U − UM
=
250 V − 80 mV
=
250 V − 0,08 V
=
249,92 V
Zum Messwerk muss der Widerstand RS in Serie geschaltet werden.
Die Größe von RS ist so zu wählen, dass an ihm bei der Stromstärke
IM
= 0,0004 A die Spannung US = 249,92 V abfällt.
US
RS
=
UM
RM
⇔
RS =
US
249,92 V
⋅ RM =
⋅ 200 Ω = 624800 Ω
0,08 V
UM
Zum Messwerk des Voltmeters muss der Widerstand RS = 624800 Ω
in Serie geschaltet werden.
Rges = RS + RM = 624800 Ω + 200 Ω = 625000 Ω = 625 kΩ
Der Gesamtwiderstand des Voltmeters beträgt Rges = 625 kΩ.
648000 Ω j 100 % ⇒ 6480 Ω j 1 % ⇒ 650000 Ω j
650000
% ≈ 100,31 %
6480
Der Gesamtwiderstand des Voltmeters Rges ist um
0,31 % g r ö ß e rals der
in Serie hinzu geschaltete Widerstand RS.
Aufgabe 4
Für den ohmschen Widerstand der Spule gilt:
R =
l
ρ⋅l
A
⇔
= 2πrn ⇔
l
=
n =
R⋅A
ρ
=
l
2πr
=
150 Ω ⋅ 0,25 mm 2
0,017
Ω mm 2
m
2205,882 m
2 π ⋅ 0,08 m
Die Windungszahl der Spule beträgt n = 4388.
≈ 2205,882 m
≈
4388