Statistik mit Excel und SPSS

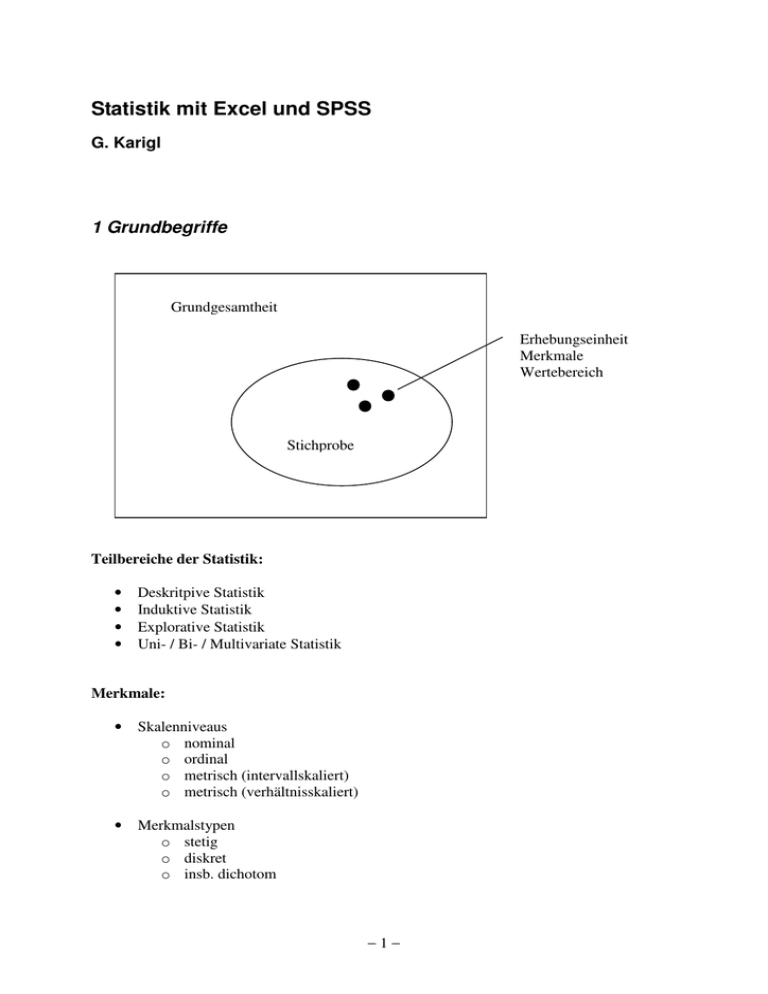
Statistik mit Excel und SPSS
G. Karigl
1 Grundbegriffe
Grundgesamtheit
Erhebungseinheit
Merkmale
Wertebereich
Stichprobe
Teilbereiche der Statistik:
•
•
•
•
Deskritpive Statistik
Induktive Statistik
Explorative Statistik
Uni- / Bi- / Multivariate Statistik
Merkmale:
•
Skalenniveaus
o nominal
o ordinal
o metrisch (intervallskaliert)
o metrisch (verhältnisskaliert)
•
Merkmalstypen
o stetig
o diskret
o insb. dichotom
−1−
Zulässige Verfahren in Abhängigkeit vom Skalenniveau:
Skalenniveau
Auszählen
Ordnen
nominal
ordinal
metrisch (Intervall)
metrisch (Verhältnis)
ja
ja
ja
ja
ja
ja
ja
Summe,
Differenz
ja
ja
Quotient
ja
Das Tabellenkalkulationsprogramm Excel:
•
•
•
Arbeitsmappen mit –blättern, Symbolleiste, Bearbeitungsleiste, aktive Zelle
Daten, Formeln (mit absolutem und relativem Zellbezug), Grafiken
Statistische Analysen: Tabellenkalkulation, Statistikfunktionen, Analysefunktionen
Das Statistikprogramm SPSS (Statistical Package for the Social Sciences):
•
•
•
•
•
Dateneditor (Daten- und Variablenansicht)
Zeilen für Erhebungseinheiten (Fälle)
Spalten für Variablen
Datenaufbereitung: Umkodieren, Transformieren, Fälle gewichten, Fälle auswählen
Datenanalyse: Analysieren, Grafiken
Viewer: Ergebnisse, Tabellen, Grafiken, Export
Lernprogramm
−2−
2 Deskriptive Statistik
2.1 Deskriptive Methoden für eindimensionale Stichproben
Stichprobe x1, x2, ..., xn vom Umfang n
bzw. geordnete Stichprobe x(l) ≤ x(2) ≤ ... ≤ x(n)
Häufigkeitsverteilungen:
•
•
Diskrete Merkmale: Urliste, Häufigkeitsverteilung
Stetige Merkmale: Klassenbildung (Gruppierung)
# Klassen ≈ √n, Klassengrenzen, Klassenmitten
Excel:
SPSS:
HÄUFIGKEIT(Datenbereich; Klassen)
(mit Strg+Umschalt+Eingabe abschließen!)
Analysieren → Deskriptive Statistiken → Häufigkeiten
Transformieren → Umkodieren in andere Variablen
Grafiken → Diagrammerstellung
Maßzahlen:
Lagemaße:
•
•
•
•
arithmetisches Mittel x =
1 n
∑ xi
n i =1
für n = 2k + 1
x (k +1)


Median xɶ =  1
für n = 2k
 2 ( x (k ) + x (k +1) )
x (k +1)
mit k = [pn], falls pn keine ganze Zahl


α-Quantil xɶ α =  1
mit k = pn, falls pn ganze Zahl
 2 ( x (k ) + x (k +1) )
Modalwert xmod
Streuungsmaße:
1 n
∑ (x i − x)2
n − 1 i =1
•
Varianz s 2 =
•
Standardabweichung s = s 2
s
Variationskoeffizient v =
x
Spannweite R = xmax − xmin
Interquartilabstand IOR = xɶ 0,75 − xɶ 0,25
•
•
•
−3−
Zulässige Maßzahlen in Abhängigkeit vom Skalenniveau:
Skalenniveau
nominal
ordinal
metrisch
(Intervall)
metrisch
(Verhältnis)
Modalwert
ja
ja
ja
Lage
Median,
Quantile
ja
ja
arithm.
Mittel
ja
Spannw.,
IQR
ja
ja
ja
ja
ja
Streuung
Varianz
ja
Var.koeff.
-
ja
ja
Excel:
MITTELWERT(Daten)
MEDIAN(Daten)
QUANTIL(Daten; α)
MODALWERT(Daten)
VARIANZ(Daten)
STABW(Daten)
SPSS:
Analysieren → Deskriptive Statistiken → Häufigkeiten
Analysieren → Deskriptive Statistiken → Deskriptive Statistiken
Analysieren → Deskriptive Statistiken → Explorative Datenanalyse
−4−
2.2 Multivariate deskriptive Statistik
Stichprobe (x1,y1), (x2,y2), ..., (xn,yn) vom Umfang n
Kontingenztafeln (insb. Vierfeldertafel):
allgemeine Form einer k × m – Kontingenztafel
b1
b2
⋯
a1
n11
n12
⋯ n1 j ⋯ n1m
n1.
a2
n 21
n 22 ⋯ n 2 j ⋯ n 2 m
n 2.
⋮
⋮
⋮
ai
n i1
ni2
⋮
⋮
⋮
ak
•
•
•
bj
⋯
⋮
⋯
n ij
bm
⋮
⋯ n im
⋮
⋮
⋮
n i.
⋮
n k1 n k 2 ⋯ n kj ⋯ n km
n k.
n .1
n
n .2
⋯ n. j
⋯ n .m
absolute und relative Häufigkeiten, Randverteilungen, bedingte Verteilungen
(n ij − n ij *) 2
niini j
2
Kontingenzkoeffizient χ = ∑
mit n ij * =
n ij *
n
i, j
χ2
∈ [ 0,1]
Kontingenzindex von Cramer V =
n(min(k, m) − 1)
SPSS:
Analysieren → Deskriptive Statistiken → Kreuztabellen
Korrelation:
s xy
∈ [ −1,1] mit s xy =
•
Korrelationskoeffizient r =
•
Rangkorrelationskoeffizient von Spearman
n
6∑ d i
rs = 1 −
Excel:
SPSS:
sxsy
1 n
∑ (x i − x)(yi − y)
n − 1 i =1
2
i =1
(n − 1)n(n + 1)
∈ [ −1,1] mit d i = R(x i ) − R(yi )
KORREL(X-Bereich; Y-Bereich)
Analysieren → Korrelation → Bivariat
Grafiken → Diagrammerstellung → Streudiagramm
−5−
Regression:
•
•
Regressionsgerade nach dem Prinzip der kleinsten Quadrate
s xy
y = a + bx mit b = 2 , a = y − bx
sx
2
Bestimmtheitsmaß r
Excel:
ACHSENABSCHNITT(Y-Bereich; X-Bereich)
STEIGUNG(Y-Bereich; X-Bereich)
BESTIMMTHEITSMASS(Y-Bereich; X-Bereich)
SCHÄTZER(x; Y-Bereich; X-Bereich)
SPSS:
Analysieren → Regression → Linear
Analysieren → Regression → Kurvenanpassung
Grafiken → Diagrammerstellung → Streudiagramm
−6−
3 Über diskrete und stetige Verteilungen
Binomialverteilung B(n, p):
•
•
n
Wahrscheinlichkeitsfunktion f (k ) = P(X = k ) =   p k q n − k , k = 0,1,..., n
k
Verteilungsfunktion F(x) = P(X ≤ x) = ∑ f (k)
k≤x
Excel:
BINOMVERT(k; n; p; 0)
BINOMVERT(x; n; p; 1)
Normalverteilung N(µ, σ):
1
1  x −µ 
− 

2 σ 
2
•
Dichtefunktion f ( x ) =
•
Verteilungsfunktion F( x ) = P(X ≤ x ) =
•
α-Quantil x = F−1 (α) (gemäß P(X ≤ x) = α )
σ 2π
e
x
∫ f ( t) dt
−∞
Excel:
NORMVERT(x; µ; σ; 0)
NORMVERT(x; µ; σ; 1)
NORMINV(α; µ; σ)
Ferner: Poissonverteilung, Hypergeometrische Verteilung
t-Verteilung, F-Verteilung, χ2-Verteilung
−7−
4 Statistische Testverfahren
Zweistichproben-t-Test für unabhängige Stichproben:
•
•
•
Modell: X1, X2 sind normalverteilt gemäß N(µ1, σ) bzw. N(µ2, σ)
Nullhypothese H0: µ1 = µ2, Alternative H1: µ1 ≠ µ2, Signifikanzniveau α
X1 − X 2
n1n 2 (n1 + n 2 − 2)
Testgröße TG =
2
2
n1 + n 2
(n − 1)S + (n − 1)S
1
•
•
1
2
2
ist t-verteilt mit n1 + n2 − 2 Freiheitsgraden
P-Wert (Signifikanz) P = P(| X |>| TG |)
Entscheidung: P < α ⇒ H0 wird verworfen
Excel:
TTEST(X1-Bereich; X2-Bereich; 2; 2)
SPSS:
Analysieren → Deskriptive Statistiken → Explorative Datenanalyse
Analysieren → Mittelwerte vergleichen → T-Test bei unabhängigen
Stichproben
χ2-Anpassungstest zum Vergleich von beobachteten und erwarteten Häufigkeiten:
•
•
•
•
•
Modell: X diskret verteilt
Nullhypothese H0: X verteilt gemäß p1, p2, ..., pk, Signifikanzniveau α
k
(n − n i *) 2
Testgröße TG = ∑ i
mit n i * = npi
ni *
i =1
ist χ2-verteilt mit k − 1 Freiheitsgraden
P-Wert (Signifikanz) P = P(X > TG)
Entscheidung: P < α ⇒ H0 wird verworfen
Excel:
CHITEST(X1-Bereich; X2-Bereich)
SPSS:
Analysieren → Nichtparametrische Tests → Chi-Quadrat
−8−