O1 Geometrische Optik Stoffgebiet: Abbildung durch Linsen

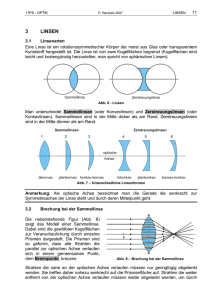
O1
Geometrische Optik
Stoffgebiet:
Abbildung durch Linsen, Abbildungsgleichung, Bildkonstruktion,
Linsensysteme, optische Instrumente ( Beleuchtungs- und
Abbildungsstrahlengang im Projektionsapparat )
Versuchsziel:
Brennweitenbestimmungen über die Linsenformel und mit Hilfe der
Besselschen Methode sollen Grundelemente der geometrischen
Optik näherbringen. Der Aufbau des Projektionsapparates soll einige
Aspekte der technischen Optik aufzeigen.
Literatur:
Lehrbücher der Physik, z.B.
Hering, Martin, Stohrer: Physik für Ingenieure S. 403 ff
Dobrinski, Krakau, Vogel: S. 264-272
Zeller-Franke: S. 429 ff, S. 448 ff
Walcher: Praktikum der Physik, S. 130 ff
1.
Grundlagen
Optische Probleme müssen grundsätzlich unter Berücksichtigung der Wellennatur des
Lichtes behandelt werden. Wenn jedoch die Wellenlänge des Lichts im Verhältnis zu
den aktuellen Abmessungen ( z.B. Objektstruktur, Linsen- und Blendendurchmesser )
als vernachlässigbar klein angenommen werden darf, wird mit Erfolg die mathematisch
einfachere geometrische Optik oder Strahlenoptik angewandt. Man spricht von
Lichtstrahlen und stützt sich auf folgende drei Elementargesetze:
Geradlinige Ausbreitung des Lichts im homogenen und isotropen Medium,
Reflexionsgesetz,
Brechungsgesetz.
Typische Wellenerscheinungen wie Interferenz und Beugung kann die geometrische
Optik nicht klären.
O1
1/14
1.1
Abbildung durch Linsen
Ein wichtiges Anwendungsgebiet der geometrischen Optik ist die optische Abbildung
durch Linsen. Linsen entstehen durch hintereinander angeordnete brechende Flächen
und sind lichtdurchlässige Körper aus einer brechenden Substanz
( Brechzahl n L ), die von gekrümmten Flächen begrenzt sind. Bei den ( technisch am
einfachsten herstellbaren ) durch Kugelflächen begrenzten Linsen nennt man die
Verbindungslinie der Kugelmittelpunkte optische Achse.
Sammel- oder Konvexlinsen ( L + ) sind in der Achse dicker, Zerstreuungs- oder
Konkavlinsen ( L - ) sind in der Achse dünner als am Rand. Vereinfacht haben diesen
beiden Linsentypen folgende Eigenschaften: Ein parallel zur optischen Achse
einfallendes Lichtbündel wird von einer Sammellinse in einem hinter L + liegendem
Brennpunkt F´ vereinigt, von einer Zerstreuungslinse so gebrochen, als ob es von
einem vor L - liegendem Brennpunkt herkäme.
F´
opt.
Achse
L+
F´
L-
1.1.1 Abbildung durch eine Sammellinse L +
Die abbildende Wirkung einer Sammellinse lässt sich vereinfacht beschreiben, wenn
man enge, achsennahe ( „paraxiale“ ) Strahlenbündel und einfarbiges
( „monochromatisches“ ) Licht voraussetzt. In der Praxis unvermeidbare Abweichungen
davon, führen zu sog. Linsenfehlern ( sphärische und chromatische Fehler ). Der
wirkliche Verlauf der Lichtstrahlen innerhalb der Linse wird durch das Brechungsgesetz bestimmt und ist sehr kompliziert. Unter den oben genannten Voraussetzungen
ist es möglich, den physikalischen Strahlengang durch einen mathematischen
Strahlengang zu ersetzen, der innerhalb der Linse wesentlich einfacher ist und
außerhalb mit dem physikalischen zusammenfällt. Der vereinfachte Strahlengang wird
durch die Einführung von sog. Hauptebenen und Brennebenen festgelegt.
O1
2/14
Gegenstandsraum
Bildraum
(ungestrichene Größen)
( gestrichene Größen)
n
n´
A (1)
y
B
D´
C´
S
H H´
S´
O
F
F´
(2)
(-)z (..)f
(-)y
A´
f´
(-)a
Abb. 1:
O´
z´
a´
Abbildung durch eine Sammellinse
( Die Punkte S, S´ nennt man Linsenscheitel; die Schnittpunkte der
Haupt- bzw. Brennebenen mit der optischen Achse sind die Hauptbzw. Brennpunkte. )
Ein vom Gegenstandspunkt A in Richtung B verlaufender und zur opt. Achse paralleler
Strahl (1) wird auf der vorderen Linsenfläche zum Einfallslot hin gebrochen. Beim
Austritt wird er vom Lot weg gebrochen und geht durch den bildseitigen Brennpunkt F´.
Der Schnittpunkt D´ der Geraden durch AB und F´C´ legt die bildseitige Hauptebene H´
fest. Durch Einführung der Hauptebene H´ wird somit die zweimalige Brechung
in B und C auf eine gedachte einmalige Brechung in D´ zurückgeführt. Analog gelangt
man zur gegenstandsseitigen Hauptebene H, wenn man den Lichtweg (2) verfolgt
( Brennstrahl Þ Parallelstrahl ). Die Abstände von Hauptebene zu Brennebene nennt
man Brennweite f bzw. f ` und von Hauptebene zu Gegenstand bzw. Bild,
Gegenstandsweite a bzw. Bildweite a`. Wenn Gegenstandsraum a und Bildraum a` im
gleichen Medium sind, ergibt sich f = - f ´ ( n = n`).
O1
3/14
Vorzeichenkonvention nach DIN 1335 für technische Strahlenoptik
Zum Rechnen mit Abständen in Gegenstands- und Bildraum ist die Festlegung der
Vorzeichen folgendermaßen vereinbart: Im Gegenstandsraum wird ein Koordinatensystem mit Ursprung in H, im Bildraum ein solches mit Ursprung in H ´ verwendet.
Gegenstandsraum
y
F
Bildraum
y`
F´
a
H
a`
H´
Abb. 2 Koordinatensystem K h , K h ´
Danach wird die Brennweite f und Gegenstandsweite a bei L + negativ (K h ), Brennweite f ` und Bildweite a` dagegen positiv ( K h´ ) bewertet. Die eingeklammerten Vorzeichen in Abb. 1 sollen an diese Regelung erinnern ( in älterer Literatur noch nicht
üblich! ).
Anmerkung:
Nach DIN 1335 können auch Koordinatensysteme mit Ursprung in F
bzw. F´ verwendet werden.
Mit den besonders ausgezeichneten Parallel- und Brennstrahlen kann bei bekannter
Lage der Haupt- und Brennebenen die eindeutige Konstruktion der optischen Abbildung
erfolgen. Ausgehend vom Gegenstand OA = y kann das Bild O`A` = y` konstruiert
werden. Der sog. Hauptstrahl AH hat zusätzlich die Eigenschaft, dass er im Bildraum
unter dem gleichen Winkel zur opt. Achse verläuft wie im Gegenstandsraum ( parallel
versetzt ).
1.1.2 “Dünne Linsen“
Bei dicken Linsen oder Linsensystemen ist die Einführung der beiden Hauptebenen
meist zwingend erforderlich. Diese können außerhalb des Linsensystems liegen oder
eng benachbart auf einer Seite des Systems. Für die Bildkonstruktion ist neben der
Angabe der Brennweite auch die Lage der Hauptebenen, von denen ab die Brennweite
gemessen wird , anzugeben. Nur bei “dünnen Linsen“ liegen die Hauptebenen H und
H´ in vernachlässigbarem Abstand etwa in der Mitte zwischen den Linsenscheiteln S
und S` und nur hier kann die Brennweite ab der Mitte gerechnet werden ( Ursprünge
von K h und K h ´ fallen zusammen ).
Bei der Abbildungskonstruktion wird aus dem parallel versetzten Hauptstrahl der
durchgezogene Mittelstrahl.
O1
4/14
1.2
Abbildungsgleichungen
Für die Sammellinse lässt sich aus Abb.1 folgende Beziehung ablesen ( Ähnlichkeit von
Dreiecken ) :
-
y¢ f z¢
= =
y z f¢
Daraus ergibt sich die sog. Newton`sche Abbildungsgleichung:
z z¢ = f f ¢
y
F
F`
H
H`
(-)y `
(-)z
Abb. 3:
(-)f
f`
z`
Ähnliche Dreiecke im Strahlengang einer Sammellinse
Bei Einführung der Gegenstandsweite a = f + z und der Bildweite a` = f ` + z `, sowie
unter Berücksichtigung von f = - f ` ( n = n`) erhält man die Linsenformel :
1
1 1 1
=- = f¢
f a¢ a
In den meisten Fällen sind bei der Berechnung nur die Beträge von a, a`, f und f `
von Bedeutung:
1
f¢
=
1
1
1
=
+
f
a¢
a
Aus Abb. 1 oder Abb. 3 lässt sich weiterhin die Beziehung
y¢ a¢
= =ß
y a
gewinnen Man nennt ß die Lateral- (Seiten-) -Vergrößerung oder den Abbildungsmasstab. Die Größe ß ist vorzeichenbehaftet; negatives ß bedeutet Bildumkehrung.
O1
5/14
1.3
Bildkonstruktion
Nach DIN 1335 wird als Lichtrichtung die Richtung von links nach rechts gewählt und
die opt. Achse strichpunktiert gezeichnet. Bei bekannter Lage der Brenn- und
Hauptebenen kann nun das Bild y` des Gegenstandes y konstruiert werden, wenn man
zwei der ausgezeichneten Strahlen ( Parallel-, Haupt- und Brennstrahl ) benutzt.
Dabei gelten folgende Regeln:
®
Brennstrahl b
Parallelstrahl p`
Parallelstrahl p ®
Brennstrahl b`
Der Hauptstrahl verläuft unter gleichem Winkel zur opt. Achse parallel versetzt.
H
H`
4`
1
2
3
4
F
F`
1` 2`
Abb. 4
3`
Bildkonstruktion mit Haupt-, Parallel- und Brennstrahl
Es ergeben sich folgende für Sammellinsen typische Eigenschaften
(Vorzeichenregelung beachten !) :
a =¥
a¢ = f ¢
Parallelstrahlen werden in f `
gesammelt
(1)
a > 2f
f ¢ < a¢ < 2 f ¢
verkleinertes Bild ( 0 > ß > -1 )
(2)
a=2f
a¢ = 2 f ¢
Bild und Gegenstand gleich groß
( ß = -1 )
(3)
(4)
2f > a > f
a¢ >2 f ¢
vergrößertes Bild ( ß < -1 )
a=f
a¢ = ¥
Bild rückt ins Unendliche (ß = - ¥ )
a <f
a¢ < 0
“virtuelles“ und aufrechtes Bild
( ß > 0 ); im Bildraum divergente
Bündel.
O1
6/14
Anmerkung:
Bei Zerstreuungslinsen L - erhält man genau dieselben Abbildungs-
gleichungen wie bei Sammellinsen, wenn man berücksichtigt, dass die Lage der
Brennebenen F und F ` vertauscht ist. Nach der Vorzeichenregelung ist daher bei
L - f `negativ und f positiv. Auch die Bildkonstruktion verläuft analog. Für Konkavlinsen ist typisch: Man erhält nur virtuelle und keine reellen Bilder.
1.4
Linsensysteme
Für ein aus zwei beliebigen Einzellinsen L1 und L2 zusammengesetztes System bei
dem
der Abstand der Hauptpunkte H1`H2 = t ist ( t > 0 ), gilt für die Berechnung der
resultierenden Brennweite f ` des Linsensystems aus den Brennweiten f1` und f2` der
Einzellinsen:
1 1
1
t
= +
f ¢ f1¢ f2¢ f1¢ • f2¢
j¢ = j1¢ + j2¢ - t • j1¢ • j2¢
oder
( Die reziproke Brennweite f -1 = j hat den besonderen Namen Brechkraft; ihre Einheit
ist die Dioptrie ( dpt );
1dpt = 1m-1 . )
Obige Formel kann zur Berechnung der Brennweite von Zerstreuungslinsen L –
verwendet werden; die Zerstreuungslinse liefert nämlich nur virtuelle Bilder und ist somit
einer direkten Brennweitenbestimmung durch Messung von Gegenstands- und
Bildweite nicht zugänglich. Man kombiniert L - mit einer Sammellinse L + bekannter
Brennweite f +` zu einem System, das noch sammelnd wirkt und die Gesamt brennweite f ` hat. Bei dünnen Sammel- und Zerstreuungslinsen, die sich in geringem
Abstand befinden
(t)
f-¢ - f+¢ ergibt sich für dir Brennweite f ` von L _ :
<<
1
1
1
=
¢
¢
fff+¢
oder
j-¢ = j¢ - j+¢
Daraus ergibt sich nach Bestimmung von f + ´ und f ´ ( Messung von Bild- und
Gegenstandsweite und Anwendung der Linsenformel ) die gesuchte Brennweite f _´ der
Zerstreuungslinse.
O1
7/14
2.
Versuchsdurchführung
Versuche mit optischen Elementen werden meist auf einer sog. optischen Bank
durchgeführt. Linsen, Lichtquellen usw. werden von “Reitern“ getragen, die an ihrem
Fuß eine Ablesemarke tragen und auf einer Schiene mit Millimetereinteilung
verschiebbar angeordnet sind. Die Ablesemarke liegt meist nicht in einer für die auf
dem Reiter befindlichen Elemente optisch relevanten Ebene. Deshalb muss in einem
Vorversuch die relative Lage von Ablesemarke zu Linsenmitte bzw. Objekt- oder
Bildebene ermittelt werden ( siehe dazu Abschnitt 2.4 ).
2.1 Bestimmung der Brennweite einer dünnen Sammellinse mit Hilfe der Linsenformel
Man beleuchtet dazu einen Gegenstand G ( Glasträger mit Millimeterskala ) durch eine
Lichtquelle L und bildet G scharf auf einem Schirm S ab. Da die Scharfstellung nur
unsicher beurteilt werden kann, werden mehrere Messungen mit unterschiedlicher
Gegenstandsweite vorgenommen. Man erhält so a` als Funktion von a . Zur
Auswertung verwendet man die Linsenformel umgeformt in:
y = x + j¢
mit y =
1
1
, x=
a¢
a
und
j¢ =
1
f¢
Dies ist die Gleichung einer Geraden mit einer Steigung 1 und einem Achsenabschnitt
j¢ . Man trägt also x gegen y in einem rechtwinkligen Koordinatensystem
gegeneinander auf und legt entweder graphisch oder numerisch eine Ausgleichsgerade
durch die
Messpunkte. Aus dem Achsenabschnitt kann dann die reziproke Brennweite j¢
entnommen werden ( s. Abb. 5 ).
Bei der Messung ist darauf zu achten, daß die
1
a¢
Messpunkte über den ganzen Messbereich
verteilt sind, d.h. es sollten stark vergrößernde
und vor allem auch stark verkleinernde Ab-
1
f¢
1
a
Abb. 5
O1
bildungen berücksichtigt werden. Nur so ist der
Fehler des Achsenabschnitts möglichst klein.
Ausgleichsgerade bei Brennweitenbestimmung mit Hilfe der Linsenformel
8/14
2.2
Bestimmung der Brennweite einer dünnen Sammellinse mit der
Besselschen Methode
Die Methode von Bessel geht davon aus, dass bei einem festen Abstand e zwischen
Gegenstand G und Schirm S ( dabei ist e > 4f ` ) zwei Linsenstellungen existieren, die
jeweils ein scharfes Bild liefern. Aus der Linsenformel folgt nämlich mit
e = a` - a = const. :
a¢2 - a¢ e + e f ¢ = 0
Dies ist eine quadratische Gleichung für a` mit den Lösungen a`1 = -a2 und a`2 = -a1 .
Die Lösungen verhalten sich so, als ob die Positionen von Bild und Gegenstand
vertauscht wären.
1
2
G
S
F `2
F `1
Bild 1
Bild 2
d
Abb. 6:
Brennweitenbestimmung mit dem Besselverfahren
Wenn man den Abstand d der beiden Linsenstellungen einführt, erhält man für die
Brennweite f ` der Linse
f¢ =
1 æ
d2 ö
• çe ÷
4 è
e ø
Ein Vorteil des Besselverfahrens ist darin zu sehen, dass bei fest eingestelltem
Abstand e zwischen G und S nur die relative Verschiebung d der beiden
Linsenstellungen gemessen wird.
O1
9/14
2.3
Aufbau eines Projektionsapparates
Die wesentlichen Elemente eines Projektionsapparates sind Lichtquelle L,
Kondensor K, Diapositiv D, Objektiv O und Bildschirm S. Das Diapositiv wird durch das
Objektiv scharf auf dem Schirm abgebildet. Die Wirkungsweise des Kondensors, der
aus einer kurzbrennweitigen Sammellinse mit großem Durchmesser besteht, lässt sich
am besten anhand einer Skizze erklären:
S
O
D
(1)
(3)
(2)
L
L`
(3)
(2)
Bild
der Lichtquelle
(1)
a) ohne Kondensor
S
O
K
D
(3)
L
L`
(2)
(2)
(3)
Bild der Lichtquelle
b) mit Kondensor
Abb. 7
Projektionsapparat mit und ohne Kondensor
Zum besseren Verständnis der Darstellung in Abb. 7 ist die bei optischen Instrumenten
häufig benutzte Unterscheidung von Beleuchtungs- und Abblildungsstrahlengang
erforderlich , je nachdem die Abbildung der Lichtquelle oder des Objekts (hier des Dias)
durch die Linsen des Instruments in Frage steht. Dabei werden nur selten die bei der
Bildkonstruktion wichtigen ausgezeichneten Strahlen ( Brenn-, Parallelstrahlen )
benutzt.
O1
10/14
(3) Beleuchtungsstrahlengang: Strahlen des Strahlenpaares (3) schneiden sich am
Ort von L und L` .
(2) Abbildungsstrahlengang:
Strahlen des Strahlenpaares (2) schneiden sich am
Ort von D und S.
Das Strahlenpaar (1) in Abb. 7a zeigt die begrenzende Wirkung der Objektivfassung auf
den abgebildeten Bereich des Dias. Der Kondensor bildet L in O ab und vergrößert so
den abgebildeten Bereich des Dias. ( Unbeeinflusst bleibt daneben der Abbildungsmaßstab bei der Abbildung des Dias durch das Objektiv auf den Bildschirm. ) Um die
Baulänge des Projektors kurz zu halten, wählt man für die Abbildung der Lichtquelle L
in der Regel ß = -1 ( symmetrische Abbildung ). Ein zweiter Vorteil des Kondensors ist
die Erhöhung der Lichtausbeute.
2.4
Messungen und Auswertungen
2.4.1 Die Brennweite einer Sammellinse L + soll nach Abschnitt 2.1 bestimmt werden.
( Es soll sich nur die Sammellinse im Linsenhalter befinden )
Dazu ist der funktionale Zusammenhang zwischen Gegenstandsweite a und
Bildweite a` für 10 bis 15 geeignet gewählte Einstellungen zu messen. Für die
Messung bei stark verkleinernder Abbildung ist die Spannung U der Lampe zu
reduzieren, da sonst wegen der zu großen Helligkeit des Bildes keine
Einzelheiten erkannt werden können. Die Brennweite f + ist aus einem
Diagramm analog Abb. 5 zu entnehmen. Durch Variation der graphisch
ermittelten Ausgleichsgeraden soll der maximale Fehler von f +
abgeschätzt werden.
æ 1ö
Δ f+ = Δ ç + ÷ • f+
èf ø
( )
2
2.4.2 Die bisher verwendete Sammellinse L + wird mit einer Zerstreuungslinse L kombiniert ( LK = L+ L - ). Die Linsenkombination LK kann im vorliegenden Fall
als dünne Sammellinse betrachtet werden. Es ist die Brennweite von LK ( fK )
mit dem Besselverfahren nach Abschnitt 2.2 zu bestimmen. Dazu sollen bei
einem fest gewähltem Abstand (e = 1000 mm) 10 unabhängige Messungen der
Linsenverschiebung d vorgenommen werden. Mittelwert und mittlerer Fehler von
d sind zu berechnen ( s. Abschnitt 2.2 in “Anleitung zur Fehlerrechnung“ ).
O1
11/14
Mit Hilfe des totalen Differentials lässt sich der Fehler von fK aus der Formel
2
æ
1
édù ö
fK = e • ç 1 - ê ú ÷ berechnen.
ç
4
ë e û ÷ø
è
¶ fK
¶ fK
ΔfK =
• Δe +
• Δd
¶e
¶d
2
¶ fK 1 æ
édù
= • ç1 + ê ú
¶ e 4 çè
ëe û
wobei
ö
÷
÷
ø
¶ fK
1 d
=- •
2 e
¶d
Einsetzen ergibt den absoluten Fehler:
2
1 æ
édù
Δ fK = • ç 1 + ê ú
4 çè
ëeû
ö
1 d
÷ • Δe + • • Δd
÷
2 e
ø
Division durch fK führt auf den relativen Fehler
Δ fK 1 + z Δ e 2 • z Δ d
=
•
+
•
fK
1- z e
1- z d
ædö
mit z = ç ÷
èeø
2
Mit fK und f + soll nach Abschnitt 1.4 ( Linsensysteme ) die Brennweite f - der
Zerstreuungslinse und deren relativen Fehler ermittelt werden:
1 1 1
= f- fK f+
Für die Fehlerabschätzung von f - wird die Formel nach f - aufgelöst:
f- =
fK • f+
f+ - fK
Die Regeln für die Fehlerfortpflanzung ergeben:
Δ f- Δ fK Δ f+ Δ f+ + Δ fK
=
+
+
ffK
f+
f+ - fK
O1
12/14
Anmerkung zu 2.4.1 und 2.4.2
Vor der Messung ist jeweils die relative Lage von Ablesemarke zu Linsenmitte,
Objektebene und Schirmebene zu bestimmen, damit die abgelesenen Werte korrigiert
werden können. Dazu wird am besten folgendermaßen verfahren: Man bildet das
Objekt so scharf ab, dass die Abbildung gut reproduzierbar ist ( z.B. starke
Vergrößerung bei der Eichung von O - und L- Reiter ). Anschließend wird eine
Reiterkante ( nicht Ablesemarke ) z.B. links abgelesen. Der Reiter wird umgedreht und
bei unveränderter Lage aller übrigen Reiter nochmals scharfgestellt. Die gleiche Kante
( jetzt rechts ) wird abgelesen. Der Mittelwert beider Ablesungen ergibt die Lage der
Linsenmitte bzw. des Objekts.
(1)
(2)
Mittelwert aus (1) und (2) ergibt die Lage der Linsenmitte
2.4.3 Aufbau eines Projektionsapparates ( Modell ) mit und ohne Kondensor
Mit einem Objektiv ( f0 = 85 mm, Æ 28 mm ) und einer Sammellinse als Kondensor
( fK = 60 mm, Æ 45 mm ) soll ein Projektionsapparat aufgebaut werden. Die
Lichtquelle ist eine Glühlampe ( vorher die auf die Lampenfassung aufgesteckte Linse
entfernen, so dass die Glühlampe( -wendel) sichtbar wird ! ). Sie wird mit der
Kondensorlinse in das Objektiv abgebildet ( ß = -1 ). Für die Abbildung des Dias soll
möglichst genau die Vergrößerung ß = -10 eingestellt werden ( Maßstab abbilden ! ).
Machen Sie am Modell die Vergrößerung des abgebildeten Bereichs des Dias deutlich
( Kondensorwirkung ) !
O1
13/14
3.
Fragen
(1)
a) Für eine Sammellinse mit f ` = - f = 32 mm und HH` = 16 mm ist die
Abbildungskonstruktion für einen Gegenstand mit y = 20 mm und
- a = 98, 64, 48, 20 mm durchzuführen.
b) Was ändert sich, wenn HH` = 0 ist ( dünne Linse ) ?
c) Führen Sie die Abbildungskonstruktion an einer Zerstreuungslinse durch mit
f = - f ` = 32 mm, HH` = 16 mm, y = 20 mm und a = - 30 mm !
(2)
Wie kann man möglichst einfach feststellen, ob eine Sammellinse als dünne
Linse behandelt werden kann ( Hinweis: zusätzliche Messung von ß ) ?
(3)
Warum soll die Kondensorlinse beim Projektor “kleine“ Brennweite und “großen“
Durchmesser haben ( Hinweis: Betrachten Sie den Zusammenhang mit
Baulänge, Lichtausbeute und Diagröße ! ) ?
(4)
Vollziehen Sie die Fehlerrechnung in Abschnitt 2.4.2 nach und ergänzen Sie die
fehlenden Schritte !
O1
14/14