Algebra - SwissEduc

Algebra
1. Erste und letzte
Gesucht ist die erste und die letzte Ziffer, sowie die totale Anzahl Ziffern der Zahl 31256
2. Tabelle
a
b
b−a
a−b
−(a + b)
−a + b
−2
−3
?
?
?
?
1
2
3
4
?
?
?
?
b
-16
|a|
?
| − b|
?
|a + b|
?
|a − b|
?
−
3. Beträge
a
10
a − |b|
?
|a| − |b|
?
4. Bruchrechnen
3
7
6
4
− − −
+
−
= ?
−
5
2
10
5
5. kgV und ggT
(a) Wie lautet das kgV der Zahlen 444, 753, 280?
(b) Wie lautet der ggT der Zahlen 123, 456, 789?
6. Multiplikation langer Zahlen
In einer Anwendung müssen häufig 12-stellige mit 8-stelligen Zahlen exakt multipliziert werden. Die
Geschwindigkeit spielt dabei keine besondere Rolle. Der zur Verfügung stehende Rechner kann aber
nur maximal 5-stellige Zahlen exakt miteinander multiplizieren. Gefragt ist eine schematische Skizze
eines Verfahren, mit dem die Multiplikationen ausgeführt werden können!
Wieviele einstellige Multiplikationen (“Aufrufen des Einmaleins”) benötigt das Verfahren?
7. Riesige Zahl
Wie lautet die letzte Ziffer der Zahl p = 123456789123456789 + 28
8. Wissenschaftliche Darstellung von Zahlen
Wie lautet die wissenschaftliche Darstellung der folgenden Zahlen?
(a) 0.0000123456789
(b) Zweimilliardensiebenhundertfünfzigmillionenzweihundertvierundneunzigtausendfünfhundertdreiundfünfzig
p
(c)
(23 · 23 · 10234 )
(d) Eine gewisse Menge des radioaktiven Materials Uran235 zerfällt in 7.04 · 108 Jahren auf die Hälfte
der ursprünglich vorhandenen Menge. Wie viele Sekunden verstreichen, bis von 100 Mikrogramm
Uran235 nur noch 25 Mikrogramm übrig sind?
9. Kürzen!
Die folgenden Brüche sind soweit als möglich zu kürzen.
75 · 119 · 54
=?
45 · 144 · 51
10. Vereinfachen
a+b a−b
−
=?
b
a
11. Vereinfachen
c
2
−
=?
c2 − 8c + 16 c2 − 6c + 8
6f 4 (gh)5
=?
(2f g)3 h2
12. Vereinfachen
a2 + c2
b−c
a−b
+
=?
−
a2 + ac ac + c2
a2 c + ac2
13. Vereinfachen
10u2 − 11u − 6
=?
25u2 − 4
14. Vereinfachen
c2 + c − 20
=?
−c2 + c + 30
15. Vereinfachen
(2s − 2r)2
7r2 s
=?
·
12(r − s)
21rs2
16. Erweitern!
Die folgenden Brüche sind entsprechend zu erweitern.
41ab5
779a3 b9
=
37a2 d4
?
3(a + b)2
?
=
2
5abcd
255a b2 c2 d2
17. Gleichnennrig
Die folgenden 3 Brüche sind gleichnennrig zu machen.
3f g 2
48f 2 g 4
18. Multiplizieren
17r4 s3 24st2
·
=?
54t5
85r2
2
3n2
7m2
·
=?
(b)
12n3
7m
(a)
19. Dividieren
9c
6ac
:
=?
10ab 25b
4uv 4
(2uv 2 )3
(b)
:
=?
4
18w
(3uw)2
(a)
20. addieren und subtrahieren
u
v
−
=?
2v 2u
13
4
(b)
=?
+1−
2
6h
21h
21. Vereinfachen
3 2
5 2
4x
a
:
2a3 b
6
y2
:
=?
1
5
(2a2 b)3 · (3x2 y 3 )3
(a)
22. vereinfachen
2
2
2 2
3b
5
2a
b +
− b2
3
2
6
3
:
=?
3
3
5a
4 2
a b
b2
3
2h5
112f gh
8
23. Der Grösse nach
Die 3 Bruchzahlen sind der Grösse nach aufsteigend zu ordnen.
9
7
7
9
10
13
24. Einfache Gleichungen
Gesucht ist die Lösung der Gleichung(en). Die Lösungsmenge ist jeweils anzugeben.
1
9
+2=
x
x
2x + 4
8x − 7
(b)
=
8
20
(a)
25. Gleichungen
Gesucht ist die Lösung der Gleichung(en). Die Lösungsmenge ist jeweils anzugeben.
2 x
27
·
=
9 11
22
15 12
(b)
·
=6
x 21
(a)
26. Kanarienvögel
1
4 Kanarienvogel frisst 125 Körner in
27. Umrechnung
15
8 kg einer Obstsorte kosten
25
22
32
3
Tagen. Wie viele Körner fressen 4 Kanarienvögel in 16 Tagen?
Fr. Wieviel kosten 3 12 kg der gleichen Sorte?
28. Von Hälften und anderen Teilen
Addiert man zu einem Drittel von einem Viertel die Hälfte von einem Fünftel und subtrahiert dann
den zehnten Teil von zwei Dritteln, so ist dieser Bruchteil einer gesuchten Zahl gleich 24. Wie lautet
die Zahl?
29. Brüche einfügen
Zwischen 18 und 19 sind 4 verschiedene Brüche einzufügen.
30. Kürzen von rationalen Ausdrücken
Wie lautet die gekürzte Darstellung des Bruches
x4 − 2x3 − 15x2 + 32x − 16
x3 − 3x2 + 3x − 1
31. Kettenbrüche
Von den beiden untenstehenden unendlich langen Kettenbrüchen sind einige Näherungswerte zu berechnen und eine Vermutung aufzustellen für den Wert des Kettenbruches. Die Vermutung soll anschliessend überprüft werden, indem eine Gleichung für den Kettenbruch aufgestellt wird.
2+
1+
1
4+
1
4+
4+
1
1
4+···
1
2+
1
3+
4+
1
1
5+···
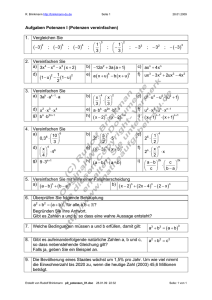
32. Unterhaltsame Potenzgesetze
Im Unterricht wurden die folgenden 5 Potenzgesetze behandelt:
• 1. Gesetz:
• 2. Gesetz:
an · am = an+m
an
= an−m
am
• 3. Gesetz:
(an )m = an·m
• 4. Gesetz:
an · bn = (a · b)n
a n
an
=
bn
b
• 5. Gesetz:
In der darauffolgenden Prüfung zu diesem Thema mussten die Schülerinnen und Schüler die Aufgabe
lösen:
’Formuliere alle 5 Potenzgesetze vollständig und korrekt in Worten.’
Nicht immer gelang es den Schülerinnen und Schülern die richtigen Worte zu finden. Welches Gesetz
wollte der Autor/die Autorin der folgenden Stilblüten wohl jeweils beschreiben? (Rechtschreibfehler
und kurlige Formulierungen sind kein Zufall!)
(a) Die Potenzen werden exponentiert, indem man den ersten Exponenten mit dem zweiten multipliziert.
(b) Potenzen werden voneinander dividiert, indem man die beiden Exponenten subtrahiert.
(c) Wenn eine Klammer vorherrscht werden die Exponenten miteinander multipliziert.
(d) Wenn man eine Zahl hoch rechnet, so kann man die beiden Exponenten multiplizieren.
(e) Wenn man zwei Variablen multipliziert, so kann man die Potenzen addieren.
(f) Potenziert man die Basis x mit n und nachher noch mit m, so behält man die Basis x und
multipliziert die Potenzen m & n miteinander.
(g) Wird eine Zahl mit der Basis x und der Potenz m mit einer Zahl der selben Basis und dem Potenz
n multipliziert, so behält man die Basis ich mit der Potenz m+n .
(h) Potenzen mit gleicher Basis und gleichem Exponent werden die Basis addiert und der Exponent
bleibt der gleiche.
(i) Bei Potenzen mit vers. Basen und gleichem Exponent wird die Basis addiert und der Exponent
bleibt. (ab ) · (cb ) = a + cb
(j) Die zwei Basen einer Multiplikation zwischen zwei Potenzen können unter dem Exponent addiert
werden wenn die zwei Exponentialzahlen gleich sind.
(k) Die Exponenten werden bei einer Multiplikation addiert indem man die Basis beibehält & die
Exponenten miteinander addiert.
(l) Bei einer Division die in einer Klammer steht wird die Hochzahl mit jedem Exponenten multipliziert.
(m) Wenn die Basis bei der Multiplikation der beiden Summanden gleich sind, aber die Potenzen
verschieden, so addiert man die Potenzen unter beihaltung der Basis.
33. Vereinfachen von Ausdrücken mit Potenzen
Die folgenden Ausdrücke sind soweit als möglich zu vereinfachen:
(a) z 2k−5 : z 3 : z k
(b) 90 · 3n−2 − 3n
5
6
x 3
: x2
(c)
4
34. Vereinfachen von Ausdrücken mit Potenzen
Die folgenden Ausdrücke sind soweit als möglich zu vereinfachen:
(3a − 1)2k−1
(1 − 3a)2k+1
2 −2 3 −2
6a b
2(cd)n cn d2n
(b)
:
·
cn+1 d2n
(ab)−1 3ab−2
(a)
(c)
x2a+5
(−y 3 )
2b+5
· [(−z)4 ]
3b+3
:
x2a
2b−1
(yz)6b+10 · [(−z)3 ]
35. Es geht auch einfacher
Gesucht ist die einfachste Form der folgenden Terme:
−1 2 −3
2a b
=?
(a)
3ac−2
u n v 3n+4 −v 2n+1
(b)
·
:
=?
v
u
u
x5 + 1 2x2 − 2 2 − x
−
+ m−2 = ?
xm+2
xm
x
2p+1 p+1 4p
z−3
5+z
z−3
(d)
·
:
=?
z+5
z−3
z+5
2 "
−1 #−2
2
1
t
(e) 1 +
·
−
−1
=?
t
t
2
(c)
36. Pascalsches Dreieck
Die folgenden Terme sind mit Hilfe des Pascalschen Dreiecks auszumultiplizieren.
(a) (a2 b − 2ab2 )4
(b) (2x2 + 4x4 )−3
37. Potenzterme vereinfachen
Die Lösung ist so anzugeben, dass sie keine negativen Exponenten enthält.
(a)
(2a)−3
4a−1 z 2
:
2
3
(x y)
(xy 2 z)−2
1
5
3
(b) −3r− 6 · r 3 : (2r 4 )2
38. Wurzelterme vereinfachen
Die Lösung ist jeweils in Wurzelschreibweise anzugeben.
√
√
3
6
(a) a−2 − 3 a−4
q
p
√
(b) 4 a3 · 3 a2 · a
√
√
6
3
(c) Radiziere teilweise und vereinfache: 80x4 − 2x 100x2
39. Vereinfachen von Ausdrücken mit Potenzen
Die folgenden Ausdrücke sind von Hand soweit als möglich zu vereinfachen:
√
√ 3
3
(a) a2 : ( a)
qp
√
(b) t t t
6
√ 1
√ 1 5
(c) 8 2 3 4 2 − 7 4 2 3
40. Quadratwurzeln
Die folgenden Ausdrücke sind soweit als möglich zu vereinfachen:
√
√ √
(a) 3rs s + 2r? s3 : s
√
√
√
√
(b)
u+v+ u−v ·
u+v− u−v
p
√
(c)
(x2 − 1) (x − 1) : x + 1
41. Vereinfachen
Die folgenden Ausdrücke sind soweit als möglich zu vereinfachen:
(x − 1)2n+1
2n+2
√
1−x
q
q
√
√
√
3
(b) m · 3 m · m · m · 6 m = ?
(a)
42. Basis gesucht
Gesucht ist bei jeder Aufgabe die Basis b.
1
(a) logb 25
=2
(b) logb 5 = 0.5
(c) logb 2 = 0
43. Ein einziger Logarithmus
Die folgenden Terme sollen durch einen einzigen Logarithmus ersetzt werden.
(a) log(ab) + log ab − log(ab)2
(b) (n + 1) · log x − 13 · log x6n
(c) 2 log u + 12 (log(u + v) + log(u − v))
44. Addition und Subtraktion
(a) 12a − (−3a) = ?
(b) 3c − 9c + (−3c) + 4c + 5c = ?
(c) −6k + 15k − 13k = ?
(d) −(−3Φ) + 5Φ − 4Φ + (−Φ) = ?
(e) (−2d + e) − (5d + 4e) − 2d + 3e = ?
(f) 12x − (12x + 3y) + (−3y) − (3x − y) = ?
(g) −6m − (4 − 6m) + 3m + (4 − 3m) = ?
(h) a − b − c − d − (a − b − c − d) + (a − b − c − d) = ?
(i) 7m − 5n − [5m − (3n − m) − (2m + n) − 5n] = ?
(j) [7a + 5b − (3a + b)] − {[3b − (2a − b)] − 5a} = ?
45. Terme vereinfachen
Die folgenden Terme sind soweit wie möglich zu vereinfachen.
(a) 1 − (2 − (3 − (4 − (5 − a)))) = ?
(b) 12q 2 − [25q 2 − (17q − 20) − 13q 2 ] − (10q − 15) = ?
(c) 7n(9n + 28) − (7n − 1)(9n + 28) = ?
(d) (60a3 b2 − 72a4 b − 48a2 b3 ) : 12a2 b = ?
46. Ausklammern
Bei den folgenden Termen ist soviel wie möglich auszuklammern.
(a) x5 − x4 − x3 − x2 =?
(b) 36g 3 h4 k 2 − 12g 4 h3 k + 66g 3 h3 = ?
47. Treppensteigen
Eine Person steigt eine Treppe mit 50 Stufen empor. Jede Stufe ist 16cm hoch und 35cm tief. Wieviel
Prozent Steigung überwindet die Person?
48. Fettgehalt
Butter hat einen Fettgehalt von 82%, Creme Fraiche enthält 30% Fett. Wie viel Gramm Butter
enthalten die gleiche Menge Fett wie ein Becher mit 125 g Creme Fraiche?
49. Abschlagen Aufschlagen
Der Preis von Äpfeln wird um 20% des bisherigen Preises gesenkt. Da die Äpfel zu dem abgesenkten
Preis reissenden Absatz finden, beschliesst der Händler, diese Äpfel wieder zu dem höheren alten Preis
zu verkaufen. Um wie viele Prozent schlagen aus Sicht des Konsumenten die Äpfel nun auf?
50. Wahlen
An einer Wahl nahmen 426’688 Wahlberechtigte teil und stimmten je für eine der 3 Parteien A, B,
oder C. Die Partei B erhielt 70% der Stimmen von A, die Partei C 80% der Stimmen von B. Wie viele
Stimmen erhielt jede der Parteien?
51. Ankauf/Verkauf
Ein Händler kauft ein Gerät ein und verkauft es an den Kunden mit 15% Rabatt. Der Kunde bezahlt
schlussendlich 1’250 Euro. Für welchen Betrag hat der Händler das Gerät im Laden zum Verkauf
angeboten? Zu welchem Preis hat er das Gerät gekauft, wenn er schlussendlich 12% Gewinn gemacht
hat?
52. Drittel-Neuntel-Rest
Ein Drittel eines Kapitals wird zu 5% angelegt. Ein weiterer Neuntel zu 4% und der Rest zu 4.5%.
Der gesamte Zinsertrag beläuft sich auf 2282.50 Euro. Wie gross ist das Anfangskapital?
53. Max und Moritz
Max und Moritz legen beide ihr Spargeld am 1. Januar auf einem Sparkonto an. Max zahlt 3312 Euro
ein und erhält einen Zinssatz von 4%. Moritz zahlt 3276 Euro auf ein Konto mit 8% Zins ein. An
welchem Tag haben sie exakt gleich viel auf dem Konto?
54. Mofa
Der Preis für ein Mofa stieg zuerst um 15%, sank dann wieder um 10% und beträgt nun 1449.- Fr. Um
wieviel % hat sich der Preis total verändert?
55. Ratenzahlung
Ein Kleinwagen kostet 15’600 Euro, wenn er bar bezahlt wird. Das Auto kann auch in zwei Raten zu
8’000 Euro bezahlt werden, wobei die erste Rate sofort und die zweite nach einem halben Jahr fällig
ist. Wieviel beträgt der Zinssatz, den der Verkäufer bei diesem Abzahlungsgeschäft verlangt?
56. Sparen
Ein Betrag von 1000 Euro wird am 1.1.06 auf ein Bankkonto mit 4% Zins angelegt. Wieviel Geld wäre
auf dem Konto, wenn man es am...
(a) ... 31. Mai 06 auflösen würde?
(b) ... 11. September 06 auflösen würde?
(c) ... 30. Dezember 06 auflösen würde?
57. Verzinsung
Welche Summe muss man heute zu 6% Zins anlegen, um in einem Jahr an Kapital und Zins 10000.Fr. zu besitzen?
58. Zinssenkung
36’000 Euro werden am 1. Februar auf ein Konto zu 5.5% Zins einbezahlt. Im Verlaufe des Jahres
wurde der Zinssatz um 0.5% gesenkt. Am Ende des Jahres konnten 1762.5 Euro an Zinsen kassiert
werden. Nach wie vielen Monaten fand die Zinssenkung statt?
59. Zwei Banken
Zwei Banken liefern sich einen Wettbewerb um die Gunst der Kunden.
A-Bank sagt: ’Bei uns bekommen sie 8% Zins auf ihre Spareinlage’.
B-Bank bietet: ’Bei uns bekommen sie zweimal im Jahr, nämlich einmal Ende Juni und einmal Ende
Dezember 4% Zins auf ihrem Konto gutgeschrieben’.
Bei welcher Bank fährt man als Kunde besser? Die Begründung ist rechnerisch zu geben.
60. Amortisation
Von einer Hypothek von 250’000 Euro muss jedes Jahr 3% der (verbleibenden) Schuld zurückbezahlt
werden (Amortisation). Wieviele Prozent der ursprünglichen Schuld sind nach 3 Jahren noch vorhanden?
61. Pascal’sches Dreieck
(a) (2a − 3b)4
(b) (1 + x)4 − (x − 1)4
62. Faktorzerlegung
Wie lautet die Faktorzerlegung des Polynoms x4 − 4x3 − x2 + 16x − 12 ?
Lösung zu: Algebra
1. Erste und letzte
erste Ziffer: 1
letzte Ziffer: 1
Anzahl Ziffern: 600
Die Berechnung kann zu (3157 )8 aufgeteilt werden, um einen Overflow im Taschenrechner zu umgehen.
Für die letzte Ziffer ist die Periodizität der Dreierpotenzen (3;9;7;1) zu berücksichtigen. Mit 1256 mod
4 = 0 folgt, dass die letzte Ziffer eine 1 sein muss.
2. Tabelle
-2; -3; -1; 1; 5; -1
− 21 ; 34 ; 54 ; − 54 ; − 14 ;
5
4
3. Beträge
10; -16; 10; 16; 6; 26; -6; -6
4. Bruchrechnen
2
−
5
5. kgV und ggT
(a) kgV = 7’801’080
(b) ggT = 3
6. Multiplikation langer Zahlen
Eine Lösung besteht darin, die Zahlen in einzelne Stücke aufzuteilen - zum Beispiel 12345678 = 1234 ·
104 + 5678 - und anschliessend die Teilprodukte zu addieren.
7. Riesige Zahl
Endzahl 7. Die Endzahlen der Potenzen von 9 sind bei ungeraden Exponenten 9 und bei geraden
Exponenten 1. Da der Exponent 123456789 ungerade ist, ist die Endzahl 9. Rechnet man noch 28
dazu, so entsteht die Endzahl 7.
8. Wissenschaftliche Darstellung von Zahlen
(a) 1.23456789 · 10−5
(b) 2.750294553 · 109
(c) 2.3 · 10118
(d) 4.4402688 · 1016 (mit 365 Tage pro Jahr gerechnet)
9. Kürzen!
35
24
10. Vereinfachen
a2 + b2
ab
11. Vereinfachen
c2 − 4c + 8
(c − 2)(c − 4)2
12. Vereinfachen
b
ac
3f g 2 h3
4
13. Vereinfachen
2u − 3
5u − 2
14. Vereinfachen
c−4
−
c−6
15. Vereinfachen
r(r − s)
9s
16. Erweitern!
779a3 b9
703a4 b4 d
153(a + b)2 abcd
255a2 b2 c2 d2
17. Gleichnennrig
21f g 2 h
336f 2 g 4 h
6f g 3 h5
336f 2 g 4 h
18. Multiplizieren
4r2 s4
45t3
3n
(b)
28
(a)
19. Dividieren
15
4a2
u4 v 2
(b)
w2
(a)
20. addieren und subtrahieren
u2 − v 2
2uv
42h2 − 8h + 91
(b)
42h2
(a)
21. Vereinfachen
625 3 2 4 1
a b x y 3
32
22. vereinfachen
10125
1024a5 b3
23. Der Grösse nach
10
7
9
13 < 9 < 7
24. Einfache Gleichungen
(a) x = 4
(b) x =
17
3
25. Gleichungen
2688f 2 g 4 h
336f 2 g 4 h
(a) x =
(b) x =
243
4
10
7
26. Kanarienvögel
3000 Körner
27. Umrechnung
70
33 Franken.
20
1 Kg kostet 33
Fr.
28. Von Hälften und anderen Teilen
1440
7
29. Brüche einfügen
mögliche Lösung:
7
41
11 43
90 ; 360 ; 60 ; 360
30. Kürzen von rationalen Ausdrücken
Durch Bestimmen der Nullstellen des Zähler- und Nennerpolynoms und Abspalten der entpechenden
Linearfaktoren erhält man
x2 − 16
(x + 4)(x − 4)(x − 1)3
=
(x − 1)3
x−1
.
31. Kettenbrüche
Der Wert des ersten Kettenbruches lässt sich einfach berechnen, indem man
x=
1
4+
1
1
4+ 4+···
setzt. Man erhält die Gleichung
x=
und damit für den Kettenbruch den Wert
√
1
4+x
5.
Der zweite Kettenbruch lässt dieses Vorgehen nicht zu und kann nicht einfach berechnet werden.
32. Unterhaltsame Potenzgesetze
(a) 3. Gesetz
(b) 2. Gesetz
(c) 3. Gesetz
(d) 3. Gesetz
(e) 1. Gesetz
(f) 3. Gesetz
(g) 1. Gesetz
(h) ziemlicher Quatsch!
(i) wohl 4. Gesetz - mit viel Phantasie!
(j) nochmals ein völlig falsch interpretiertes 4. Gesetz?
(k) 1. Gesetz
(l) 5. Gesetz
(m) 1. Gesetz
33. Vereinfachen von Ausdrücken mit Potenzen
(a) z k−8
(b) 3n+2
(c)
x9
234
34. Vereinfachen von Ausdrücken mit Potenzen
Die folgenden Ausdrücke sind soweit als möglich zu vereinfachen:
(a) −
1
(3a − 1)2
(b) 25 3a6 cn−3
(c)
x5
y5 z5
35. Es geht auch einfacher
27a6
8b6 c6
v 3
(b) −
u
2x2 + 1
(c)
xm+2
3p
z+5
(d)
z−3
(a)
(e) (t − 2)2
36. Pascalsches Dreieck
(a) a8 b4 − 8a7 b5 + 24a6 b6 − 32a5 b7 + 16a4 b8
1
(b)
64x12 + 96x10 + 48x8 + 8x6
37. Potenzterme vereinfachen
(a)
32a2
x8 y 7
(b) − 34
38. Wurzelterme vereinfachen
√
(a) −2 · 3 a12
√
24
(b)
a23
√
√
(c) 0; Der Term lässt sich teilweise radizieren auf: 2x 3 10x − 2x 3 10x
39. Vereinfachen von Ausdrücken mit Potenzen
(a) a−5/6
(b) t7/8
(c) 2
40. Quadratwurzeln
(a) 5rs
(b) 2v
(c) x − 1
41. Vereinfachen
(a) −(1 − x)n
√
3
(b) m4
42. Basis gesucht
1
⇒ b = 15
(a) b2 = 25
√
(b) b = 5 ⇒ b = 25
(c) b0 = 2 ⇒ nicht lösbar!
43. Ein einziger Logarithmus
(a) log a·b·a
− 2 log(ab) =
b
log a2 − log(a2 b2 ) =
2
log aa2 b2 = log b12
(b) log xn+1 − log x2n = log
xn+1
x2n
= logx1−n
√
(c) logu2 + 12 log(u2 − v 2 ) = log(u2 u2 − v 2 )
44. Addition und Subtraktion
(a) 15a
(b) 0
(c) −4k
(d) 3Φ
(e) −9d
(f) −3x − 5y
(g) 0
(h) a − b − c − d
(i) 3m + 4n
(j) 11a
45. Terme vereinfachen
(a) 3 − a
(b) 7q − 5
(c) 9u + 28
(d) 5ab − 6a2 − 4b2
46. Ausklammern
(a) x2 (x3 − x2 − x − 1)
(b) 6g 3 h3 (6hk 2 − 2gk + 11)
47. Treppensteigen
45.71%
Horizontaldifferenz: 17.5m; Höhendifferenz: 8m
48. Fettgehalt
45.73g
125g Creme Fraiche enthalten 37.5g Fett.
49. Abschlagen Aufschlagen
25%
50. Wahlen
A 188’800
B 132’160
C 105’728
A erhält 100 ’Teile’, B 70 und C 56. Das sind total 226 ’Teile’. Ein ’Teil’ entspricht somit 1’888
Wählerstimmen.
51. Ankauf/Verkauf
angeschriebener Verkauspreis: 1470.60 Euro
1250 Euro entsprechen 85%
Ankaufspreis: 1116.05 Euro
1250 Euro entsprechen 112%.
52. Drittel-Neuntel-Rest
49’000 Euro
Kaptial x Euro ⇒ 13 · x · 0.05 +
1
9
· x · 0.04 +
5
9
· x · 0.045 = 2282.5
53. Max und Moritz
100 Tage
Ansatz: Zins Max + 36 = Zins Moritz
54. Mofa
Der Preis ist um 3.5% gestiegen
55. Ratenzahlung
10.526% Jahreszins
Der Verkäufer leiht dem Käufer 7600 Euro für ein halbes Jahr und verlangt dafür eine ’Gebühr’ von
400 Euro.
56. Sparen
(a) 1016.666 Euro (5 Monate)
(b) 1027.888 Euro (251 Tage)
(c) 40 Euro (ein Jahr)
57. Verzinsung
9433.95 Fr.
58. Zinssenkung
7.5 Monate
x: Anzahl Monate zu 5.5%; (11-x): Anzahl Monate zu 5%
x
36000 · 0.055 · 12
+ 36000 · 0.05 · (11−x)
= 1762.5
12
59. Zwei Banken
B-Bank ist besser.
A-Bank: 1000*0.08 = 80 Euro Zins
B-Bank: Zinseszins! Total 81.6 Euro Zins.
60. Amortisation
91.2673%
61. Pascal’sches Dreieck
(a) 16a4 − 96a3 b + 216a2 b2 − 216ab3 + 81b4
(b) 8x3 + 8x
62. Faktorzerlegung
Zugehörige Polynomfunktion hat Nullstellen x1 = 1, x2 = 2, x3 = −2, x4 = 3, also (x − 1)(x − 2)(x +
2)(x − 3)