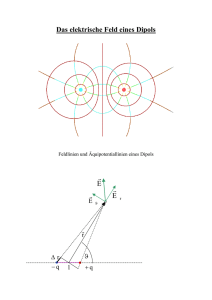
Das Feld eines elektrischen Dipols

Ergänzungen zu Physik II
Das Feld eines elektrischen Dipols
Das Feld eines elektrischen Dipols
z
Wir betrachten zwei entgegengesetzt geladene
Teilchen, deren Ladungen den gleichen Betrag haben (|q+ | = |q− | =: q). Unser Ziel ist es, das
von ihnen erzeugte elektrische Feld zu beschreiben, wobei wir die folgenden Schritte vornehmen:
6
g3 r P
ggggg
g
g
g
g
ggggg
q+ u
gggg~rg
g
A
g
g
g
g
d~ 6
r−
gAgggg
0
A
ϑ A
u
1
q− )=
d · cos(ϑ)
r+
- x
1) Bestimmung von V (r)
~ r) = −gradV
2) Berechnung von E(~
Schritt 1)
V (r)
::::::::::
∂V
6 Er = − ∂r
und damit
1
1
−
r+
r−
V(r)
V (r) = V+ + V−
q+
q−
1
+
=+
4π0 r+
r−
q
1
1
=+
−
,
4π0 r+
r−
1
1
−
r+
r−
+q
4π0
·
1
r
wobei r− ∼
= r+ + d · cos(ϑ)
-r
r
d · cos(ϑ)
d · cos(ϑ)
r+ + d · cos(ϑ) − r+ ∼
∼
=
.
=
=
r+ r−
r+ 2 + r+ d cos(ϑ)
r+ 2 (1 + rd+ cos(ϑ))
Für r+ , r− d ist r+ ' r sowie
V =
d
r+
cos(ϑ) 1 , also
d · cos(ϑ)
∼
=
r2
q
d · cos(ϑ)
=⇒ V (r) ∼
.
·
=+
4π0
r2
Führen wir nun die Definition des Dipolmoments p~ := q · d~ ein, so lässt sich das Potential schreiben als
V (r) ∼
=
1
1
1
1
pr cos(ϑ)
p~ ◦ ~r
=
· 3 · qd r cos(ϑ) =
·
· 3 .
3
4π0 r |{z}
4π0
r
4π0
r
|~
p|
|
{z
}
p~ ◦ ~r
Diskussion: Indem wir cos(ϑ) als cos(ϑ) =
V (r) =
z
r
(1)
beschreiben, finden wir für die obige Näherung die Form
1
p · cos(ϑ)
p
z
·
=
· 3.
2
4π0
r
4π0 r
(2)
Für ϑ = π/2, d.h. in der ganzen xy-Ebene (denn dort ist z = 0), gilt folglich V (r) = 0 = konst. – die
~ senkrecht
xy-Ebene ist also eine Äquipotentialfläche. Dies wiederum bedeutet, dass das elektrische Feld E
zur xy-Ebene steht; es ist Ex = Ey = 0.
1
Ergänzungen zu Physik II
Das Feld eines elektrischen Dipols
Schritt 2)
::::::::::
~ r) = −gradV , d.h. es ist mit Gl.(2) z.B. die x-Komponente
E(~
Ex
∂V
p 0 · r3 − z ·
= −
·
= −
∂x
4π
r6
| {z 0}
∂(r 3 )
∂x
,
=:A
und da r =
p
x2 + y 2 + z 2 , ist
3
∂(r )
∂x
2 1√
= 3r2 ∂(r)
∂x = 3r · 2
Ex = −Az
2
= 3x rr = 3xr , woraus folgt:
x
3xr
= −3Az · 5 .
r6
r
Ey = −3Az ·
Analog dazu ist
2x
x2 +y 2 +z 2
(3)
y
.
r5
(4)
Tatsächlich gilt mit den gefundenen Ausdrücken wie erwartet Ex (z = 0) = Ey (z = 0) = 0 4. Für die
z-Komponente findet man schliesslich
Ez = −
1 · r3 − z ·
∂V
= A·
∂z
r6
∂(r 3 )
∂x
= A·
r3 − z · 3zr
r3
= A· 6
6
r
r
woraus sich für z = 0 die Beziehung Ez (z = 0) =
A
r3
1−
3z 2
r2
=
A
3z 2
·
1
−
, (5)
r3
r2
ergibt.
2