Klasse 11 Aufgaben zum zentralen Stoß - Robert-Koch

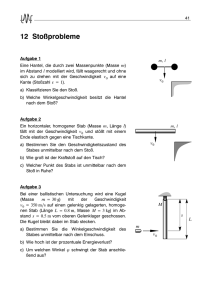
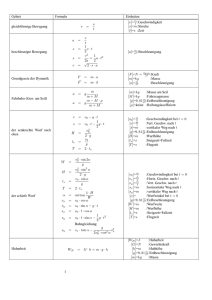
Klasse 11
Aufgaben zum zentralen Stoß– 1 –
April
(WWG)
1. Ein Schüler der Masse m = 60 kg springt mit der Geschwindigkeit v = 5, 0 ms in
Fahrtrichtung auf einen Wagen der Masse M = 200 kg. Beide zusammen rollen
anschließend mit der Geschwindigkeit v 0 reibungsfrei auf der waagerechten Straße
weiter.
a) Um welche Art von Stoß handelt es sich bei dem Vorgang?
b) Welche Geschwindigkeit v 0 hat der Wagen nach dem Auftreffen des Schülers?
2. Umkehrung nach v: Ein Schüler der Masse m = 60 kg springt in Fahrtrichtung auf
einen Wagen der Masse M = 150 kg. Beide zusammen rollen anschließend mit der
Geschwindigkeit v 0 = 1, 5 ms reibungsfrei auf der waagerechten Straße weiter.
Mit welcher Geschwindigkeit v ist der Schüler auf den Wagen aufgesprungen?
3. Umkehrung nach m: Ein Schüler der Masse springt mit der Geschwindigkeit v =
5, 0 ms in Fahrtrichtung auf einen Wagen der Masse M = 100 kg. Beide zusammen
rollen anschließend mit der Geschwindigkeit v 0 = 1, 4 ms reibungsfrei auf der waagerechten Straße weiter.
Welche Masse hat der Schüler?
4. Aus einem Gewehr der Masse M = 4, 0 kg wird ein Geschoss der Masse m = 10 g mit
einer Geschwindigkeit von v = 750 ms abgefeuert.
a) Berechne die Rückstoßgeschwindigkeit des Gewehrs.
b) Der Schütze bremst das Gewehr innerhalb von 0, 1 s ab. Welche mittlere Kraft
wirkt während dieser Zeit auf den Schützen?
c) Formuliere alle Möglichkeiten, wie die Aufgabenstellung von a umgekehrt werden
kann.
5. Ein Neutron der Masse m1 = 1, 67 · 10−27 kg stößt gerade, zentral und elastisch mit
einem ruhenden Stickstoffkern der Masse m2 = 14 · m1 . Das Neutron hat vor dem
Stoß die Geschwindigkeit v1 = 1, 96 · 107 ms .
a) Welche Geschwindigkeit u1 hat das Neutron nach dem Stoß?
b) Mit welcher Geschwindigkeit u2 bewegt sich der Stickstoffkern nach dem Stoß?
6. Ein Neutron der Masse m1 = 1, 67 · 10−27 kg stößt gerade, zentral und elastisch
mit einem ruhenden Atomkern. Das Neutron hat vor dem Stoß die Geschwindigkeit
v1 = 1, 96 · 107 ms , nach dem Stoß u1 = 1, 66 · 107 ms .
a) Welche Masse m2 hat der Atomkern?
b) Drücke diese Masse durch m1 aus.
7. Zwei Kugeln der Massen M = 500 g und m = 100 g
fallen wie rechts gezeichnet aus einer Höhe von h =
1, 5 m herab und prallen vollelastisch gegen den Fußboden. Die Radien der Kugeln werden hierbei vernachlässigt.
Wie hoch steigt die Kugel der Masse m nach dem
Aufprall am Fußboden wieder nach oben?
m
M
Klasse 11
Aufgaben zum zentralen Stoß– 2 –
April
(WWG)
8. Ein Tischtennisball der Masse m = 20 g fliegt mit einer Geschwindigkeit von v1 = 20 ms
auf den gegnerischen Tischtennisschläger zu, der sich seinerseits mit einer Geschwindigkeit von v2 = 10 ms auf den Ball zubewegt. Die Masse des Schlägers ist im Vergleich
zu der des Balles praktisch unendlich groß. Der Aufprall des Balles sei vollelastisch.
Welche Geschwindigkeit hat der Ball nach dem Kontakt mit dem Schläger?
9. Eine Gewehrgeschoss der Masse m = 1, 5 g wird in einen ruhenden, an zwei dünnen
schnüren aufgehängten Holzklotz der Masse M = 400 g geschossen. Der Holzklotz
wird dadurch wie ein Pendel ausgelenkt. Die maximal horizontale Verschiebung seines
Schwerpunkts aus der Ruhelage beträgt d = 30 cm. Die Schnüre haben eine Länge
von r = 1, 50 m.
a) Berechne die Höhe h, um die der Holzklotz durch den Einschuss maximal angehoben wird. Dabei darf davon ausgegangen werden, dass h gegenüber r sehr
klein ist.
b) Berechne die Geschwindigkeit v des Geschosses vor dem Auftreffen auf den Holzklotz. Hier kann in die Rechnung eingehen, dass m sehr klein gegenüber M ist.
Vo r d e m A u ftreffen:
Im U m k e h rp u n k t d e s P e n d e ls:
H o lz k lo tz
r
M
m
G e sc ho ss
Z e iger
d
reibungsfrei rollender Güterwaggon der
10. Ein mit der Geschwindigkeit v1 = 5, 0 km
h
Masse m1 = 18 t fährt auf einen zweiten, ruhenden der Masse m2 = 12 t auf und
kuppelt ein. Beide fahren reibungsfrei weiter.
a) Welche Art von Stoß liegt vor?
b) Welche Geschwindigkeit u haben beide Waggons nach dem Zusammenkuppeln?
11. Bei einem Regenschauer treffen pro Sekunde 1000 Regentropfen mit einer Geschwindigkeit von v = 120 km
senkrecht auf ein Dachfenster der Fläche A = 1, 5 m2 . Die
h
Tropfen haben eine Masse von m = 0, 12 g.
a) Welche Kraft F wird durch den Aufprall auf das Fenster ausgeübt? (ohne
Schwerkrafteinfluss des Wasserfilms!)
b) Welchen Druck p üben die Tropfen durch den Aufprall auf das Fenster aus?
Hilfe: 2. Newtonsches Gesetz: F · ∆t = ∆p.
Viel Erfolg !
Kink
Klasse 11
Aufgaben zum zentralen Stoß– 1 –
(WWG)
Musterlösung – 1 –
1. geg: m = 60 kg, M = 200 kg, v = 5, 0 ms .
a) Es handelt sich um einen vollkommen unelastischen Stoß.
b) Impulserhaltung:
mv = (M + m) v 0
60 kg
m
m
m
·v =
· 5, 0 = 1, 2
v0 =
M +m
200 kg +60 kg
s
s
2. geg: m = 60 kg, M = 150 kg, v 0 = 1, 5 ms .
mv = (M + m) v 0
M + m 0 150 kg +60 kg
m
m
·v =
· 1, 5 = 5, 3
v=
m
60 kg
s
s
3. geg: M = 100 kg, v = 5, 0 ms , v 0 = 1, 4 ms .
mv = (M + m) v 0
mv = v 0 M + v 0 m
m (v − v 0 ) = v 0 M
1, 4 ms
v0
m=
·M =
· 100 kg = 39 kg
v − v0
5, 0 ms − 1, 4 ms
4. geg: M = 4, 0 kg, m = 10 g, v = 750, 0 ms , V 0 = 1, 4 ms , ∆t = 0, 1 s.
a) Impulserhaltung:
mv = M v
m
0, 010 kg
m
m
v=
·v =
· 750 = 1, 9
M
4, 0 kg
s
s
b) Kraftstoß=Impulsänderung:
F · ∆t = ∆p
F · ∆t = mv
0, 010 kg ·750 ms
mv
F =
=
= 75 N
∆t
0, 1 s
Alternativ: Bewegungsgleichung:
a=
v
∆t
0, 010 kg ·750 ms
v
mv
f =m·a=m·
=
=
= 75 N
∆t
∆t
0, 1 s
April
Klasse 11
Aufgaben zum zentralen Stoß– 1 –
(WWG)
Musterlösung – 2 –
4.
c)
April
i. Aus einem Gewehr wird ein Geschoss der Masse m = 10 g mit einer Geschwindigkeit von v = 750 ms abgefeuert. Das Gewehr wird dabei mit
v = 1, 9 ms zurückgestoßen.
Berechne die Masse des Gewehrs.
ii. Aus einem Gewehr der Masse M = 4, 0 kg wird ein Geschoss mit einer
Geschwindigkeit von v = 750 ms abgefeuert. Das Gewehr wird dabei mit
v = 1, 9 ms zurückgestoßen.
Berechne die Masse des Geschosses.
iii. Aus einem Gewehr der Masse M = 4, 0 kg wird ein Geschoss der Masse
m = 10 g abgefeuert. Das Gewehr wird dabei mit v = 1, 9 ms zurückgestoßen.
Berechne die Geschwindigkeit des Geschosses.
5. geg: m1 = 1, 67 · 10−27 kg, m2 = 14 · m1 , v1 = 1, 96 · 107 ms .
a) Vollelastischer gerader Stoß:
m1 v1 + m2 (2v2 − v1 )
m1 v1 + m2 (2 · 0 − v1 )
m1 v1 − m2 v1
=
=
m1 + m2
m1 + m2
m1 + m2
7m
(m1 − 14 · m1 ) · 1, 96 · 10 s
(m1 − m2 ) v1
m
=
=
= −1, 7 · 107
m1 + m2
m1 + 14 · m1
s
u1 =
b) Für u2 gilt entsprechend:
m2 v2 + m1 (2v1 − v2 )
m2 · 0 + m1 (2v1 − 0)
2v1 m1
=
=
m1 + m2
m1 + m2
m1 + m2
7m
2 · 1, 96 · 10 s · m1
m
=
= 2.6 · 106
m1 + 14 · m1
s
u2 =
6. geg: m1 = 1, 67 · 10−27 kg, v1 = 1, 96 · 107 ms , u1 = −1, 66 · 107 ms (Vorzeichen!).
a) Vollelastischer gerader Stoß:
m1 v1 + m2 (2v2 − v1 )
m1 v1 + m2 (2 · 0 − v1 )
=
m1 + m2
m1 + m2
m1 v1 − m2 v1
u1 =
m1 + m2
u 1 m 1 + u1 m 2 = m 1 v 1 − m 2 v 1
m2 (v1 + u1 ) = m1 (v1 − u1 )
1, 96 · 107 ms + 1, 66 · 107 ms
v1 − u1
m2 =
· m1 =
· m1
v1 + u1
1, 96 · 107 ms − 1, 66 · 107 ms
u1 =
= 12 · m1 = 12 · 1, 67 · 10−27 kg
b) Aus Teilaufgabe a:
m2 = 12 · m1
Klasse 11
Aufgaben zum zentralen Stoß– 1 –
(WWG)
Musterlösung – 3 –
April
7. geg: Kugel 1: m1 = M = 500 g, Kugel 2: m2 = m = 100 g, h = 1, 5 m.
Unmittelbar vor dem Aufprall auf dem Fußboden haben beide Kugeln die Geschwindigkeit v:
v 2 = 2gh
p
v2 = − 2gh
= −5, 4
m
(nach unten)
s
√
Nach dem alleinigen Aufprall von Kugel 1 hat diese die Geschwindigkeit
v
=
2gh
1
√
und stößt elastisch und gerade mit Kugel 2 der Geschwindigkeit v2 = − 2gh = −v1 .
Nach dem Stoß hat Kugel 2 dann die Geschwindigkeit
−m2 v1 + m1 (2v1 + v1 )
−m2 v1 + 3m1 v1
m2 v2 + m1 (2v1 − v2 )
=
=
m1 + m2
m + m2
m +m
√1
√ 1 2
(−m2 + 3m1 ) v1
(3m1 − m2 ) 2gh
(3M − m) 2gh
m
=
=
=
= 12, 7
m1 + m2
m1 + m2
M +m
s
u2 =
Steighöhe h0 von Kugel 2:
u22 = 2gh0
u22
(3M − m)2
(3M − m)2 (2gh)
=
=
·h
2g
2g (M + m)2
(M + m)2
(3 · 500 g −100 g)2
=
· 1, 5 m = 8, 2 m
(500 g +100 g)2
h0 =
8. geg: Ball: m1 = m = 20 g, v1 = 20 ms , Schläger: m2 = M m1 , v2 = 10 ms .
Im System des Tischtennisschlägers trifft der Ball mit einer Geschwindigkeit von
v1 + v2 auf und wird reflektiert, d.h. er hat nachher die Geschwindigkeit − (v1 + v2 ).
Weil sich der Schläger selbst aber mit −v2 (nach links) bewegt, ist die Geshwindigkeit
des Balles gegenüber dem ruhenden System −v1 − 2v2 = −20 ms − 2 · 10 ms = −40 ms ,
also dem Betrage nach 40 ms .
Alternativ als elastischer gerader Stoß mit anschließendem Grenzübergang M → ∞:
mv1 + M (2v2 − v1 )
m+M
mv1 + M (2v2 − v1 )
m
m
m
lim u1 = lim
= 2v2 − v1 = 2 · −10
− 20 = −40
M →∞
M →∞
m+M
s
s
s
u1 =
Klasse 11
Aufgaben zum zentralen Stoß– 1 –
(WWG)
Musterlösung – 4 –
April
9. geg: Ball: m = 1, 5 g, M = 400 g, r = 1, 50 m, d = 30 cm.
Eine Gewehrgeschoss der Masse m = 1, 5 g wird in einen ruhenden, an zwei dünnen
schnüren aufgehängten Holzklotz der Masse M = 400 g geschossen. Der Holzklotz
wird dadurch wie ein Pendel ausgelenkt. Die maximal horizontale Verschiebung seines
Schwerpunkts aus der Ruhelage beträgt d = 30 cm. Die Schnüre haben eine Länge
von r = 1, 50 m.
r
r-h
d
h
a) Hypotenusensatz des Pythagoras:
r2
r2
h2 − 2rh + d2
−2rh + d2
= (r − h)2 + d2 ,
= r2 − 2rh + h2 + d2 ,
= 0. Da h r folgt:
≈ 0,
h=
d2
(0, 30 m)2
=
= 0, 030 m = 3, 0 cm .
2r
2 · 1, 50 m
b) Energieerhaltung, dabei ist u die anfängliche Geschwindigkeit des Klotzes:
1
(M + m) u2 = (M + m) gh,
2
p
u = 2gh.
Impulserhaltung beim unelastischen Stoß des Geschosses auf den Klotz:
mv = (M + m) u,
(M + m)
(M + m) p
v=
u=
2gh. Da m M folgt:
m
mr
Mp
400 g
m
m
m
v≈
2gh =
· 2 · 9, 81 2 · 0, 030 m = 205 ≈ 200 .
m
1, 5 g
s
s
s
Klasse 11
Aufgaben zum zentralen Stoß– 1 –
(WWG)
Musterlösung – 5 –
April
10. geg: m1 = 18 t, v1 = 5, 0 km
, m2 = 12 t.
h
a) Es handelt sich um einen vollkommen inelastischen Stoß. (Die überschüssige
Energie muss von Stoßdämpfern in den Puffern in Wärme umgewandelt werden.)
b) Impulserhaltung:
m1 v1 = (m1 + m2 ) u
18 t
km
km
m1
u=
· v1 =
· 5, 0
= 3, 0
m1 + m2
18 t +12 t
h
h
11. geg: m = 0, 12 g, v = 120 km
= 33, 3 ms , A = 1, 5 m2 , n = 1000.
h
a) Kraftstoß = Impulserhaltung während der Zeit ∆t = 1, 0 s:
F · ∆t = ∆p
F · ∆t = n · m · v
F =
1000 · 0, 12 · 10−3 kg ·33, 3 ms
n·m·v
=
= 4, 0 N
∆t
1s
b) Druck:
p=
F
4, 0 N
=
= 2, 7 Pa = 0, 027 mbar
A
1, 5 m2