Kongruenz von Figuren - minus-p

Kongruenz von Figuren
Kongruenz von Figuren
Definition: Zwei Figuren sind kongruent (deckungsgleich), wenn sie in der Form und
Größe übereinstimmen.
Schreibweise: A { B
Bedeutung: lateinisch: congruens = übereinstimmend, passend
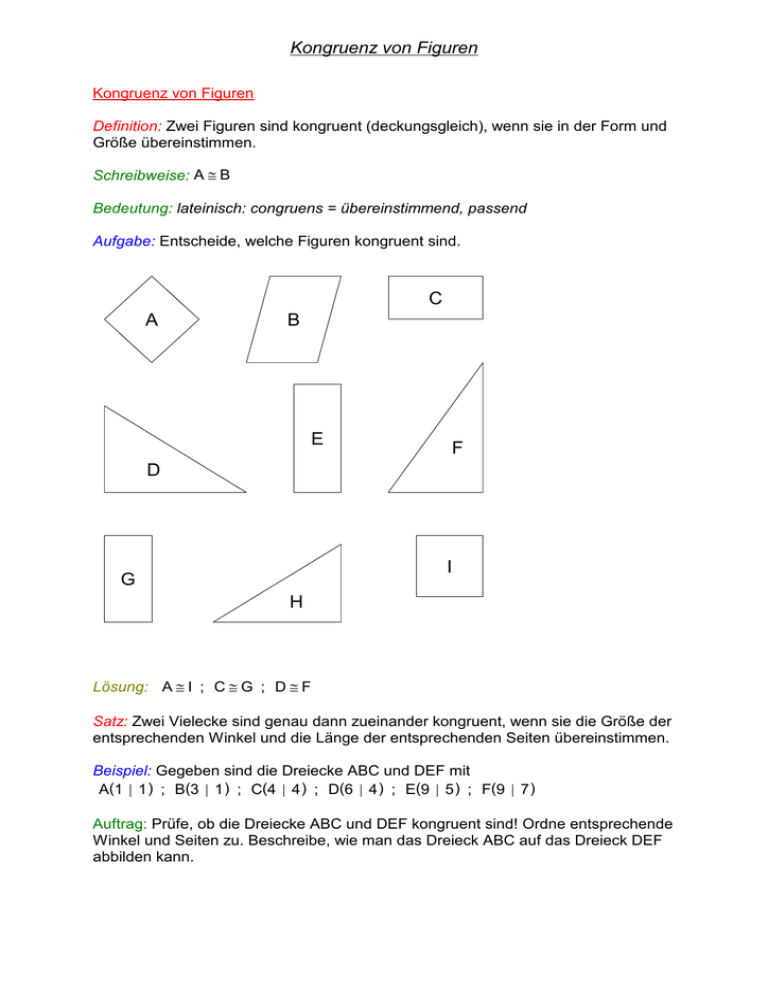
Aufgabe: Entscheide, welche Figuren kongruent sind.
C
A
B
E
F
D
I
G
H
Lösung: A { I ; C { G ; D { F
Satz: Zwei Vielecke sind genau dann zueinander kongruent, wenn sie die Größe der
entsprechenden Winkel und die Länge der entsprechenden Seiten übereinstimmen.
Beispiel: Gegeben sind die Dreiecke ABC und DEF mit
A(1 x 1 ) ; B(3 x 1 ) ; C(4 x 4 ) ; D(6 x 4 ) ; E(9 x 5 ) ; F(9 x 7 )
Auftrag: Prüfe, ob die Dreiecke ABC und DEF kongruent sind! Ordne entsprechende
Winkel und Seiten zu. Beschreibe, wie man das Dreieck ABC auf das Dreieck DEF
abbilden kann.
Kongruenz von Figuren
Erkenntnis: Vielleicht hast du erkannt, dass man das Dreieck durch eine Spiegelung
an einer Geraden und einer Drehung um den Punkt D aufeinander abbilden kann.
Immer wenn das gelingt, hat man ebenfalls nachgewiesen, dass Original- und
Bildfigur kongruent zueinander sind. Das halten wir in dem nächsten Satz fest.
Satz: Zwei Figuren sind zueinander kongruent, wenn sie durch eine Spiegelung,
Verschiebung oder Drehung aufeinander abgebildet werden können.
Aufgaben: S. 153 Nr. 9/10/11/12
Lösung: S. 153 Nr. 9
«ABFE { «ABFE
«BCGF { «ADHE
«EFGH { «ABCD
In einem Würfel sind alle Seitenflächen kongruent.
< ABS { <BCS
< ABS { <CDS
< ABS { <ADS
Kongruenz von Figuren
Lösung: S. 153 Nr. 10 a)
S. 153 Nr. 10 b)
S. 153 Nr. 10 c)
Lösung: S. 153 Nr. 11
Verschiebung
Achsenspiegelung:
Kongruenz von Figuren
Drehung um 180° bzw. Punktspiegelung:
Achsenspiegelung:
Lösung: S. 153 Nr. 12
a)
b)
c)
d)
e)
f)
g)
wahr
falsch
wahr
falsch
wahr
wahr
wahr