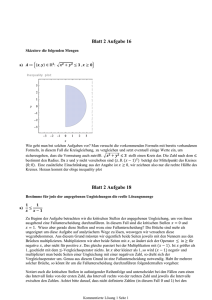
Konstanz des Produkts

Vorlesung zur Arithmetik
• V1 18./19.04.
• V2 -./26.04.
•
V3
02./03.05.
•
V4
09./10.05.
•
V5
16./17.05.
•
•
•
V6
V7
V8
23./24.05.
30.05./31.05.
06./07.06.
•
•
V9 20./21.06.
V10 27./28.06.
•
•
•
V11 04./05.07.
V12 11./12.07.
V13 18. 07.
Arithmetik in der Grundschule
Die Entwicklung des Zahlbegriffs
beim Kind/Konzepte für den
Anfangsunterricht
Natürliche Zahlen im
Anfangsunterricht
Die Grundrechenoperationen Addition
und Subtraktion
Die Grundrechenoperationen
Multiplikation und Division
Rechengesetze und Rechenstrategien
Rechenfakten automatisieren
Natürliche Zahlen und ihre
Eigenschaften
Schriftliche Rechenverfahren
Rechenschwäche und
Rechenbegabung
Aufgabenformate und Übungsangebote
Zusammenfassung und Überblick
Klausur
1
Programm
• 1 Rechengesetze und Rechenregeln beim
Multiplizieren und Dividieren
• 2 Rechenstrategien für das Multiplizieren und
Dividieren
2
1 Rechengesetze, mathematische
Zusammenhänge, Rechenregeln
• Zusammenhang zwischen den
Operationen
• Kommutativgesetz der Multiplikation
• Assoziativgesetz der Multiplikation
• Distributivgesetz der Multiplikation
bezüglich der Addition
3
Der Zusammenhang zwischen Multiplikation
und Division in N wird genutzt, um
Quotienten zu berechnen.
4
Beobachtungen beim Teilen in Kl. 2: Additives Denken
unterstützt die Prozesse beim Teilen
Kommutativgesetz der Multiplikation
• Es gilt 3·4=4+4+4=12 und 4·3=3+3+3+3=12, d.h., 4·3=3·4.
• Die Faktoren eines Produkts dürfen vertauscht werden, ohne
dass sich das Ergebnis ändert.
• Für alle natürlichen Zahlen a, b gilt:
a·b=b·a
Veranschaulichung
Leonardo/Diesterweg
6
Assoziativgesetz der Multiplikation
• Sind drei Zahlen miteinander zu multiplizieren, so sind
zunächst zwei von ihnen zu multiplizieren und dieses
Produkt dann mit der dritten. Dabei ist die Reihenfolge der
Zusammenfassung ohne Einfluss auf das Ergebnis, z. B.:
• 4·2·3 = (4·2)·3 = 8·3 = 24
• 4·2·3 = 4·(2·3) = 4·6 = 24
• Anwendungsbeispiele:
12 · 6
s. Vorlesung
3 · 28
4 · 50
Für alle natürlichen
Zahlen a, b, c gilt:
(a·b)·c = a·(b·c)
7
Die Multiplikationstabelle
lässt folgende
Vermutungen zu:
- Die Multiplikation in N
ist kommutativ.
- 1 ist das neutrale
Element der
Multiplikation.
- a · 0 = 0 · a ist
allgemeingültig in N.
8
Distributivgesetz
• Dieses Gesetz der Verteilung drückt einen Zusammenhang
zwischen Rechenoperationen verschiedener Stufe aus:
5·(4+3) = 5·4 + 5·3.
• Es beschreibt, wie sich bei der Multiplikation einer Summe
der andere Faktor auf die Summanden verteilt
(Distributivgesetz der Multiplikation bezüglich der
Addition).
• Für alle natürlichen Zahlen a, b, c gilt:
a · (b + c) = a · b + a · c
Aus dem Distributivgesetz sind ableitbar die Beziehungen:
• (a – b) · c = a · c – b · c
• (a + b) : c = a : c + b : c
c 0
• (a - b) : c = a : c – b : c
c 0
Für natürliche Zahlen a, b, c sind diese Gleichungen nur sinnvoll, wenn
die Subtraktion a - b und die Division a : c und b : c ausführbar sind.
9
Veranschaulichung
2 · (3+4) = 2 · 3 + 2 · 4
• Anwendungsbeispiele:
– 12 · 6
– 3 · 28 s. Vorlesung
– 4 · 50
10
Veranschaulichung
6·9
6 · (5 + 4) = 6 · 5 + 6 · 4
11
Hinzu kommen Betrachtungen zur Konstanz
des Produkts und des Quotienten:
• Konstanz des Produkts (gegensinniges Verändern)
•
z. B.: Das Produkt bleibt gleich, wenn man einen Faktor verdoppelt und den
anderen halbiert (sofern dies im Bereich der natürlichen Zahlen möglich ist).
• 6·8 = 12·4 = 3·16 = 24·2 = 48·1 = 96·0,5 ...
• 24·50 = 12·100 ...
• Konstanz des Quotienten (gleichsinniges Verändern)
•
z. B.: Der Quotient bleibt gleich, wenn man den Dividenden verdoppelt und den
Divisor verdoppelt.
• 12:2 = 24:4 = 48:8 = ...
• 24:4 = 240:40 = ...
12
Weitere Beziehungen
• Verdoppelt man in einem Produkt einen
Faktor, so verdoppelt man das Produkt
insgesamt.
3·8=24
6·8=48
• Halbiert man in einem Produkt einen Faktor,
so halbiert man das Produkt insgesamt.
3·8=24
3·4=12
13
Beispiele
• 4·50
• 4·(5·10)=(4·5) ·10
• (2·2)·50=2·(2·50)
Assoziativgesetz
• 4·50
• 4·(25+25)=4·25+4·25
• 4·(100-50)=4·100-4·50
Distributivgesetz
• 4·50
• 2·100
Konstanz des Produkts
•
•
•
•
3·24
3·(20+4)
3·(3·8)
6·12
6·9
(2·3) ·9
6·(10-1)
3 · 9 = 27
dann ist 6 · 9 = 54
14
Ausführbarkeit der Division
• Die Division ist im Bereich der natürlichen Zahlen
nicht immer ausführbar.
z. B. 17 : 5
3 · n = 17 (3·5=15; 3·6=18); 17=3·5+2.
• Durch Null kann nicht dividiert werden.
5 : 0 = n würde bedeuten n · 0 = 5. Für jede Zahl n ist ein
solches Produkt aber 0.
Auch mit Dividend 0 nicht möglich, da kein eindeutiges
Ergebnis zugeschrieben werden kann: 0:0=? (0:0=17, weil
17·0=0 oder 0:0=183, weil 183·0=0 oder ...)
15
Die Divisionstafel lässt
folgende Vermutungen zu:
- Die Division in N ist nicht
stets ausführbar. Es
bleiben Felder leer.
- Die Division in N ist nicht
kommutativ. Es liegt keine
Symmetrie bezüglich der
Hauptdiagonalen vor.
-In jedem Feld der
Hauptdiagonalen steht die
Zahl 1; stets gilt a : a = 1.
-Es gibt keine zur
Eingangszeile gleiche Zeile.
Die erste Spalte ist leer.
Quotienten a:0 existieren
nicht.
16
2 Rechenstrategien
2.1 Rechenstrategien für das
Multiplizieren
2.2 Rechenstrategien für das Dividieren
17
2.1 Rechenstrategien für das
Multiplizieren
•
schrittweise
39·6 = 180 + 54 = 234
30·6
9·6
Distributivität
123·7=700+140+21=861
100·7
20·7
3·7
18
schrittweise
18·30= 540
18·3·10
Assoziativität
34·4 = 136
34·2·2
Assoziativität
19
Aufgabe vereinfachen
16· 50 = 800
8·100
Konstanz des
Produkts
20
Mit einer Hilfsaufgabe rechnen
• 39·6
40·6 - 1·6
• 17·19
17·20 - 17·1
• 17·21
17·20 + 17·1
• 37· 5
37·10 = 370 Die Hälfte ist 185.
Distributivität
Wenn ich einen Faktor
verdopple, verdoppelt sich
das Produkt.
21
Multiplizieren mit dem Malkreuz
(stellenweises Rechnen)
130
+
52
140
+
42
= 182
22
Rechenstrategien für das
Multiplizieren
• schrittweise
• Aufgabe vereinfachen
• Hilfsaufgabe
• Malkreuz (stellenweises Rechnen)
Probieren Sie die Strategien für die folgenden
Aufgaben aus: 38 · 8; 24 · 12.
23
2.2 Rechenstrategien für das
Dividieren
•
schrittweise
• 54:3 = 10+8 = 18
30:3
24:3
• 956:4 = 239
800:4 = 200
120:4 = 30
36:4 = 9
Distributivität
956: 4 = 239
400: 4 = 100
400: 4 = 100
120: 4 = 30
36: 4 = 9
24
Hilfsaufgabe
54:3=20-2=18
60:3
6:3
956:4=250-11=239
1000:4
44:4
Wird von Schülern kaum angewendet.
Distributivität
25