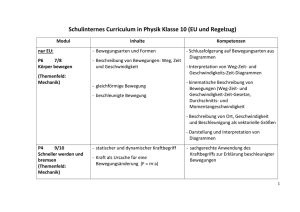
exphys_skript_teil1

Experimentalphysik A
fr
Chemie- und Elektroingenieure
von
Frank Frenzel
Karsten Kth
Hartmut Kuttruf
Was wir wissen ist ein Tropfen,
was wir nicht wissen ein Ozean.
(Isaac Newton)
Inhaltsverzeichnis
0.1
0.2
0.3
0.4
Vorwort . . . . . . . . .
Inhalt Teil B . . . . . .
griechische Buchstaben .
Zehnerpotenzen . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1.1 Kinematik des Punktes . . . . . . . . . . . . . . . . . . . . . . .
1.1.1 Geschwindigkeit . . . . . . . . . . . . . . . . . . . . . .
1.1.2 Beschleunigung . . . . . . . . . . . . . . . . . . . . . . .
1.1.3 Die gleichf
rmig beschleunigte Bewegung . . . . . . . .
1.1.4 Bewegungen in zwei oder drei Dimensionen . . . . . . .
1.2 Grundgesetze der klassischen Mechanik . . . . . . . . . . . . .
1.2.1 Die drei Newtonschen Axiome . . . . . . . . . . . . . . .
1.2.2 Trgheitsprinzip und Inertialsysteme
(Erstes Newtonsches Axiom) . . . . . . . . . . . . . . .
1.2.3 Kraft, Masse und Impuls
(Zweites Newtonsches Axiom) . . . . . . . . . . . . . . .
1.2.4 Kraft und Gegenkraft, Schwerelosigkeit
(Drittes Newtonsche Axiom) . . . . . . . . . . . . . . .
1.2.5 Die quivalenz von schwerer und trger Masse . . . . .
1.2.6 Reibungskrfte . . . . . . . . . . . . . . . . . . . . . . .
1.3 Drehbewegung / Rotation . . . . . . . . . . . . . . . . . . . . .
1.3.1 Kinematik der Drehbewegung . . . . . . . . . . . . . . .
1.3.2 Scheinkrfte im gleichf
rmig rotierenden Bezugssystem .
1.4 Arbeit, Leistung, Energie und Krfte . . . . . . . . . . . . . . .
1.4.1 Arbeit . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4.2 Leistung und Wirkungsgrad . . . . . . . . . . . . . . . .
1.4.3 Potentielle Energie . . . . . . . . . . . . . . . . . . . . .
1.4.4 Kinetische Energie . . . . . . . . . . . . . . . . . . . . .
1.4.5 Der Energieerhaltungssatz (EES) . . . . . . . . . . . . .
1.4.6 konservative und nicht konservative Krfte . . . . . . .
1.4.7 Kraft und Potential . . . . . . . . . . . . . . . . . . . .
1.5 Schwingungen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5.1 Die harmonische Schwingung . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1 Mechanik
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
7
8
8
9
9
9
10
11
12
14
14
. . . 14
. . . 15
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
16
16
16
17
17
19
20
20
21
21
23
23
23
23
24
24
INHALTSVERZEICHNIS
4
1.6
1.7
1.8
1.9
1.10
1.11
1.5.2 Die harmonische Schwingung einer Hookschen Feder . . . . .
1.5.3 Energieerhaltung bei einer harmonischen Schwingung . . . .
1.5.4 Das mathematische Pendel . . . . . . . . . . . . . . . . . . .
Impulserhaltung und Stogesetze . . . . . . . . . . . . . . . . . . . .
1.6.1 Der Impulserhaltungssatz . . . . . . . . . . . . . . . . . . . .
1.6.2 Der Schwerpunkt (oder Massenmittelpunkt) . . . . . . . . . .
1.6.3 gerader, elastischer Sto . . . . . . . . . . . . . . . . . . . . .
1.6.4 gerader, zentraler inelastischer Sto . . . . . . . . . . . . . .
1.6.5 nicht zentraler Sto mit m1 = m2 . . . . . . . . . . . . . . . .
Die Physik der Drehbewegung . . . . . . . . . . . . . . . . . . . . . .
1.7.1 Drehbewegung eines Massenpunktes . . . . . . . . . . . . . .
1.7.2 kinetische Energie . . . . . . . . . . . . . . . . . . . . . . . .
1.7.3 Leistung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.7.4 Hebelgesetz . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.7.5 Formulierung des 2. Newtonschen Gesetzes fr die Drehbewegung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.7.6 Gegenberstellung von Translation und Rotation . . . . . . .
1.7.7 Der Drehimpulserhaltungssatz . . . . . . . . . . . . . . . . .
Die Mechanik starrer K
rper . . . . . . . . . . . . . . . . . . . . . .
1.8.1 Trgheitsmoment ausgedehnter K
rper . . . . . . . . . . . . .
1.8.2 Der Satz von Steiner . . . . . . . . . . . . . . . . . . . . . . .
1.8.3 Zylinder auf schiefer Ebene . . . . . . . . . . . . . . . . . . .
1.8.4 Translation und Rotation rollender K
rper . . . . . . . . . .
1.8.5 vektorielle Schreibweise bei Drehbewegungen . . . . . . . . .
1.8.6 Der Kreisel . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.8.7 Gleichgewicht am starren K
rper . . . . . . . . . . . . . . .
1.8.8 Hooksches Gesetz der Torsion, Drehschwingung . . . . . . . .
Gravitation und Keplersche Gesetze . . . . . . . . . . . . . . . . . .
1.9.1 Das Newtonsche Gravitationsgesetz . . . . . . . . . . . . . .
1.9.2 Feldstrke, Potential und potentielle Energie im Gravitationsfeld . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.9.3 Bestimmung der Gravitationskonstanten . . . . . . . . . . .
1.9.4 Planetenbahnen und Keplersche Gesetze . . . . . . . . . . . .
1.9.5 Gebundene und ungebundene Zustnde . . . . . . . . . . . .
Deformation fester K
rper . . . . . . . . . . . . . . . . . . . . . . . .
1.10.1 Dehnung und Zugversuche . . . . . . . . . . . . . . . . . . . .
1.10.2 Spannung, Dehnung und Hooksches Gesetz . . . . . . . . . .
1.10.3 Querkontraktion . . . . . . . . . . . . . . . . . . . . . . . . .
1.10.4 Kompressibilitt . . . . . . . . . . . . . . . . . . . . . . . . .
1.10.5 Scherung und Torsion . . . . . . . . . . . . . . . . . . . . . .
1.10.6 Elastische Energie und Energiequelle . . . . . . . . . . . . . .
Ruhende Flssigkeiten und Gase (Hydrostatik und Aerostatik) . . .
1.11.1 Druck in ruhenden Flssigkeiten (ohne Gravitation) . . . . .
25
25
26
26
26
26
27
27
28
28
28
29
29
30
30
31
31
32
32
33
34
34
35
35
37
38
39
39
39
40
40
41
41
41
42
43
44
44
46
46
46
INHALTSVERZEICHNIS
5
1.11.2 Gravitation bei Flssigkeiten: der Schweredruck . . . . . . .
1.11.3 Auftrieb Prinzip von Archimedes . . . . . . . . . . . . . . . .
1.11.4 p(h) bei Gasen: die barometrische H
henformel . . . . . . . .
1.11.5 Oberchenspannung und Kapillaritt . . . . . . . . . . . . .
1.12 Str
mende Flssigkeiten und Gase (Hydrodynamik und Aerodynamik)
1.12.1 Die Kontinuittsgleichung (inkompressible Str
mung) . . . .
1.12.2 Potentielle und kinet. Energie in str
menden Medien: die
Bernoulli-Gleichung . . . . . . . . . . . . . . . . . . . . . . .
1.12.3 Viskose Str
mung zwischen Platten . . . . . . . . . . . . . .
1.12.4 Laminare Str
mung durch Rohre das Gesetz von HagenPoiseuille . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.12.5 Stokesche Reibung einer Kugel . . . . . . . . . . . . . . . . .
1.12.6 Turbulente Str
mung und Reynolds-Zahl . . . . . . . . . . .
1.12.7 Luftwiderstand und cw -Wert . . . . . . . . . . . . . . . . . .
2 Schwingungen
2.1 Freie und erzwungene Schwingungen . . . . . . .
2.1.1 Schwingungsarten . . . . . . . . . . . . .
2.1.2 Die Bewegungsgleichung . . . . . . . . . .
2.1.3 Dierentialgleichungen . . . . . . . . . . .
2.1.4 Der harmonische Oszillator . . . . . . . .
2.1.5 Gegenberstellung verschiedener
harmonischer Schwingungen . . . . . . . .
2.1.6 Der freie, gedmpfte Oszillator . . . . . .
2.1.7 Erzwungene Schwingungen und Resonanz
2.1.8 Einschwingvorgnge . . . . . . . . . . . .
2.2 berlagerung von Schwingungen . . . . . . . . .
2.2.1 berlagerung paralleler Schwingungen . .
2.2.2 berlagerung orthogonaler Schwingungen
2.2.3 Fourier-Synthese und Fourier-Analyse . .
2.2.4 Gekoppelte Schwingungen . . . . . . . . .
3 Wellen
3.1 Von Schwingungen zu Wellen . . . . . . . .
3.2 Die Wellengleichung . . . . . . . . . . . . .
3.3 Wellenarten . . . . . . . . . . . . . . . . . .
3.3.1 Longitudinale Wellen . . . . . . . . .
3.3.2 Transversale Wellen . . . . . . . . .
3.3.3 Ebene- und Kugelwellen . . . . . . .
3.3.4 Beugung und Huygenssches Prinzip
3.3.5 Stehende Wellen . . . . . . . . . . .
3.4 Beispiel einer mechanischen Welle . . . . . .
3.5 Energietransport durch die Welle . . . . . .
3.6 Der Dopplereekt . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
47
47
48
49
50
50
51
53
53
54
54
55
57
58
58
58
58
59
59
60
62
63
63
63
65
67
67
71
71
72
72
72
72
72
72
73
74
75
75
INHALTSVERZEICHNIS
6
3.7 Kohrenz und Interferenz . . . . . . . . . . . . . . . . . . . . . . . . 76
3.8 Dispersion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
4 Thermodynamik
4.1 Wrmeenergie und Temperatur . . . . . . . . . . . . . . . . . .
4.1.1 Temperatur und der Nullte Hauptsatz . . . . . . . . . .
4.1.2 Temperaturskala / absoluter Nullpunkt . . . . . . . . .
4.1.3 Wrmeausdehnung . . . . . . . . . . . . . . . . . . . . .
4.1.4 Technische Verfahren zur Temperaturmessung . . . . . .
4.1.5 Wrmeenergie und spezische Wrme . . . . . . . . . .
4.1.6 Phasenumwandlungen und latente Wrme . . . . . . . .
4.1.7 Phasendiagramme . . . . . . . . . . . . . . . . . . . . .
4.1.8 Ideale und reale Gase . . . . . . . . . . . . . . . . . . .
4.1.9 Die Zustandsgleichung fr ideale Gase . . . . . . . . . .
4.2 Mikroskopische Denition des idealen Gases . . . . . . . . . . .
4.2.1 kinetische Gastheorie . . . . . . . . . . . . . . . . . . . .
4.2.2 Maxwellsche Geschwindigkeitsverteilung . . . . . . . . .
4.3 Partialdruck, Dampfdruck, Luftfeuchtigkeit . . . . . . . . . . .
4.3.1 Daltonsches Gesetz der Partialdrcke . . . . . . . . . .
4.3.2 Dampfdruck . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.3 Siedepunkt . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.4 Relative Luftfeuchtigkeit im Taupunkt . . . . . . . . . .
4.4 Reale Gase: van der Waalsche Zustandsgleichung . . . . . . . .
4.5 Joule - Thomson - Eekt und Gasverssigung nach Linde . .
4.6 Zustandsnderungen und Kreisprozesse idealer Gase . . . . . .
4.6.1 Der erste Hauptsatz der Thermodynamik . . . . . . . .
4.6.2 Die spezischen Molwrmen Cp und Cv idealer Gase . .
4.6.3 Zustandsnderungen idealer Gase . . . . . . . . . . . . .
4.6.4 Der Carnotsche Kreisproze . . . . . . . . . . . . . . . .
4.6.5 Energiebilanz und Wirkungsgrad der Carnot - Maschine
4.6.6 Die rckwrts laufende Carnot - Maschine . . . . . . . .
4.6.7 Stirling - Proze und Heiluftmotor . . . . . . . . . . .
4.6.8 Technische Khlschrnke und Wrmepumpe . . . . . .
4.6.9 Transport von Wrmeenergie . . . . . . . . . . . . . . .
4.7 Entropie und der zweite Hauptsatz . . . . . . . . . . . . . . . .
4.7.1 Formulierung des zweiten Hauptsatzes . . . . . . . . . .
4.7.2 Reversible und irreversible Prozesse . . . . . . . . . . .
4.7.3 Reduzierte Wrme und Entropie . . . . . . . . . . . . .
4.7.4 Nullpunkt der Entropie und dritter Hauptsatz . . . . .
4.7.5 Der berstr
mversuch von Gay - Lussac . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
77
77
77
77
78
79
79
79
80
81
82
82
83
84
85
85
85
85
85
86
86
87
87
87
88
91
93
94
95
95
96
96
96
97
97
98
98
0.1. VORWORT
7
0.1 Vorwort
Mit dieser Mitschrift wollen wir die Reihe der im Internet erhltlichen Skripte ergnzen und es den H
rern der Experimentalphysik fr Chemie- und Elektroingenieure
empfehlen. Da es trotz Fehlerkorrektur m
glich ist, da sich Fehler eingeschlichen
haben, freuen wir uns ber konstruktive Kritik.
Die Mitschrift haben wir unter Linux mit LYX, einer graschen Oberche zu LATEX,
erstellt.
Dieses Skript und sein Nachfolgeskript Experimentalphysik B sind unter
http://www.uni-karlsruhe.de/upix erhltlich.
Frank Frenzel
Karsten K
th
Hartmut Kuttruf
0.2 Inhalt Teil B
1. Elektrizitt und Magnetismus
(a) Elektrostatik
(b) Magnetostatik
(c) Elektrodynamik
2. Optik
(a) geometrische Optik
(b) Wellenoptik
(c) Quantenoptik
3. Aufbau der Materie
(a) Atome und Molekle
(b) Festkrper
(c) Kerne
[email protected]
[email protected]
[email protected]
INHALTSVERZEICHNIS
8
0.3 griechische Buchstaben
"
#
A Alpha
B Beta
; Gamma
Delta
E Epsilon
Z Zeta
H
Eta
Theta
o
$
I
Jota
K Kappa
Lambda
M
My
N
Ny
Xi
O Omikron
Pi
%
&
'
!
P Rho
Sigma
T Tau
Y Ypsilon
Phi
X Chi
Psi
Omega
Vorsilbe
Deka
Hekto
Kilo
Mega
Giga
Tera
Peta
Dezi
Zent
Milli
Mikro
Nano
Piko
Femto
Abkrzung
da
h
k
M
G
T
P
d
c
m
n
p
f
0.4 Zehnerpotenzen
Potenzschreibweise Dezimalschreibweise
101
10
2
10
100
103
1 000
106
1 000 000
9
10
1 000 000 000
1012
1 000 000 000 000
1015
1 000 000 000 000 000
;
1
10
0,1
;
2
10
0,01
;
3
10
0,001
10;6
0,000 001
10;9
0,000 000 001
;
12
10
0,000 000 000 001
10;15
0,000 000 000 000 001
Kapitel 1
Mechanik
1.1 Kinematik des Punktes
1.1.1 Geschwindigkeit
mittlere Geschwindigkeit
x=0
x2
x1
x(t1) = x1
x(t2) = x2
x = x(t2 ) ; x(t1) = x2 ; x1 zurckgelegter Weg
t = t2 ; t1 dafr ben
tigte Zeit
vm = x(tt22);;xt1(t1 ) = xt
: v] = 1 ms
mittlere Geschwindigkeit oder Durchschnittsgeschwindigkeit.
Momentangeschwindigkeit v
Idee: Wir machen die Zeit t immer kleiner.
x(t2 );x(t1)
v =t2lim
!t1 t2 ;t1 Momentangeschwindigkeit
x
oder v =lim
t!0 t
In der Physik ist die Geschwindigkeit meist die Momentangeschwindigkeit.
Weg-Zeit-Diagramm:
x(t)
t1
t2
t
9
KAPITEL 1. MECHANIK
10
Geschwindigkeit-Zeit-Diagramm:
v(t)
t1
t2
t
Die Steigung im Weg-Zeit-Diagramm als Momentangeschwindigkeit:
x(t)
x(t)
∆x
α
∆t
s
vm = xt =tan x = (t) =x_
v =lim
dt
t!0 t
t
dt innitesimal
Die Geschwindigkeit ist die Ableitung des Ortes nach der Zeit.
x_ = tan gibt die Steigung der Tangente an die x(t)-Kurve zum Zeitpunkt t
an.
Dies gilt auch fr beliebige x(t).
1.1.2 Beschleunigung
Geschwindigkeit: nderung des Weges als Funktion der Zeit.
Beschleunigung: nderung der Geschwindigkeit als Funktion der Zeit ?
mittlere Beschleunigung am :
am = v(t2t2);;vt1(t1) = vt
Einheit: m
a] = vt]] = 11ss = 1 sm2
momentane Beschleunigung:
v(t2);v(t1 )
v = dv =_v
a =t2lim
dt
!t1 t2;t1 =lim
t!
0 t
2 x(t)
d
dx
dv
a(t) = dt = dt ( dt ) = dt2 =x(t)
1.1. KINEMATIK DES PUNKTES
11
allgemein
v(t)
v(t)
∆v
α
∆t
t
a ist die Steigung im v(t)-Diagramm, a kann auch negativ sein. Bei negativem
a mu jvj nicht geringer werden, da das Vorzeichen auch von der Wahl des Bezugssystems abhngen kann.
v = a t
allgemein fr a(t) gilt:
dv = a(t) dt
P a(t )t
v =lim
i i
ti !0
Schreibweise als Integral
Rt
v = a(t) dt v(t ) =
2
2
t1
v(t
1)
|{z}
2
+
Integrationskonstante
ebenso beim Weg:
v = dx
x = v t
dtR
x = v(t)dt
Rt2
x(t2) = x(t1)+ v(t)dt
Zt
t1
a(t)dt
| {z }
Aufsum: innitesimaler Geschw:aenderungen
dx = v(t)dt
t1
1.1.3 Die gleichfrmig beschleunigte Bewegung
Die Grundformeln
v(t = 0) = 0
x(t = 0) = 0
a = const:
v(t)
v(t)
t
v = at
x = vm t = v(t);2 v(0) t
x = at2;0 t
x = 12 a t2
gilt nur bei a = const:
Rt
Rt
0
0
oder : x = v(t)dt = (at)dt
KAPITEL 1. MECHANIK
12
Rt
= a t dt = 21 a t2
0
R
allg.: tn dt =
1 n+1
n+1 t
v = at (1)
q
x = 12 a t2 ) t2 = 2ax ) t = 2ax
q p
(2)in(1) v = a 2ax = 2ax
(2)
Das Superpositionsprinzip in einer Dimension
Bewegungsablufe lassen sich bertragen.
Beispiel: Anfangsgeschwindigkeit: v0 , Anfangskoordinaten: x0
=) x(t) = x0 + v0 t + 12 a t2
und v(t) = v0 + at
Dabei kann auch v0 < 0 und a = 0 sein.
Anwendungen:
senkrechter Wurf
Fugnger mit vF = const:
1.1.4 Bewegungen in zwei oder drei Dimensionen
Superpositionsprinzip in 2 oder 3 Dimensionen
Eine Bewegung lt sich in Teilbewegungen zerlegen.
Die Teilbewegungen laufen unabhngig voneinander ab und beeinussen sich
nicht gegenseitig.
Die Summe der Teilbewegungen ergibt die Gesamtbewegung.
=) Die Bewegungen in x-, y-, und z- Richtung lassen sich v
llig unabhngig
voneinander beschreiben.
Beispiele
Freier Fall
waagrechter Wurf
Freier Fall aus der H
he H, v0 = 0
v(t) = gt im Schwerefeld der Erde.
h(t) = H ; g2 t2
Fallzeit: qt(h = 0) = 0 = H ; 12 g t2
=) t = 2gH
Zerlegung in 2 Teilbewegungen:
freier Fall in z-Richtung z(t) = ; 21 g t2
konstante Bewegung mit vx in x-Richtung
1.1. KINEMATIK DES PUNKTES
13
x(t) = vx t ) t = xv(xt)
(2) z(t) = ; 12 g vxx22 = ; 21 vgx2 x2
Wurfparabel (z(x) = const x2 )
(1)
z
x
Wurfparabel
Die vektorielle Darstellung
Idee: unabhngige Beschreibung der Teilbewegungen
x(t) = x0vx t = ax t2
y(t) = y0 vy t = ay t2
z(t) = z0 vz t = az t2
0als xVektoren:
1 0x 1 0vx1 0a 1
0
0
x
B@ y C
A = B@ y0 CA + B@ v0y CA t + 12 B@ ay CA t2
z
z0
v0 z
az
oder kurz: ~r = ~r c + ~v0 t + 12 ~a t2
011
Vektoren haben Einheiten! z.B.: ~a= B
@ 2 CA sm2
3
1.Vektor - 2.Vektor (Verschiebungsvektor)
1.Vektor
2.Vektor
Die mittlere Geschwindigkeit zeigt in die Richtung des Verschiebungsvektors!
Wir betrachten zwei Arten physikalischer Gr
en:
Skalare (nur Betrag)
Vektoren (Betrag + Richtung)
KAPITEL 1. MECHANIK
14
1.2 Grundgesetze der klassischen Mechanik
1.2.1 Die drei Newtonschen Axiome
1. Erstes Newtonsches Axiom
Trgheitsprinzip (siehe auch 1.2.2)
Ein K
rper verharrt im Zustand der Ruhe oder der gleichf
rmig geradlinigen
Bewegung, solange keine resultierende Kraft auf ihn einwirkt.
P
d.h. ~v = const: falls F~i = 0 (fr m = const:)
2. Zweites Newtonsches Axiom
Aktionsprinzip (siehe auch 1.2.3)
F~ = m~a , ~a = mF~
P
~ Kraft
F:
F~ = i F~i
m : Masse
~a : Beschleunigung
Die Beschleunigung eines K
rpers ist umgekehrt proportional zu seiner Masse
und direkt proportional zur resultierenden Kraft, die auf ihn einwirkt.
allgemeinere Formulierung:
F~ = p~ ~p = m~v
3. Drittes Newtonsches Axiom
Reaktionsprinzip (siehe auch 1.2.4)
actio = reactio
Krfte treten immer paarweise auf. bt ein K
rper A auf einen K
rper B eine
Kraft F aus, so bt K
rper B eine betragsmig gleiche, aber entgegengesetzte
Kraft auf K
rper A aus.
1.2.2 Trgheitsprinzip und Inertialsysteme
(Erstes Newtonsches Axiom)
)
~r
_
sind immer in Bezug auf ein Koordinatensystem deniert.
~v = ~r
_
~a = ~v ~r
Ein solches Koordinatensystem, auf das man sich bei der Beschreibung einer Bewegung bezieht, heit Bezugssystem.
Ein unbeschleunigtes Bezugssystem heit Inertialsystem.
In allen relativ zu einem Inertialsystem mit ~v = const: bewegten Koordinatensystemen gilt das erste Newtonsche Axiom und folglich gilt:
~v1 = const:!~v2 = const: ) ~v1 + ~v2 = const: ) Jedes solches System ist
ebenfalls Inertialsystem.
In einem relativ zu einem Inertialsystem beschleunigten Bezugssystem
gilt das 1. Newtonsche Axiom nicht, da dies kein Inertialsystem ist.
1.2. GRUNDGESETZE DER KLASSISCHEN MECHANIK
15
Die Erde kann nur nherungsweise als Inertialsystem angesehen werden. Das
1. Newtonsche Axiom gilt nicht exakt, wegen der Erdrotation.
Dies fhrt zur sogenannten Corioliskraft.
1.2.3 Kraft, Masse und Impuls
(Zweites Newtonsches Axiom)
Masse: m
m] = 1 kg
Messung der Masse ber die Gewichtskraft: F = m g
Vergleich mit der Gravitationskraft, die auf ein Massennormal, das Ur-Kilogramm
,
wirkt.
Kraft: F
F~ = m~a
F] = m]a] = 1kg sm2 = 1N
Messung der Kraft:
1. Vergleich mit der Gewichtskraft einer bekannten Masse.
2. Messung mit Hilfe einer Federwaage (Hooksches Gesetz)
Die Ausdehnung einer Feder ist proportional der lngs ihrer Achse wirkenden
Zugkraft.! F = D x D: Federkonstante
x: Auslenkung der Feder
Achtung: Dies ist kein Naturgesetz, gilt nur nherungsweise und fr kleine
Auslenkungen.
Impuls
~p = m~v
p] = m]v] = 1 kgsm
Die allgemeine Form des 2. Newtonschen Axioms
F~ = p~ = dtd (m~v ) (Produktregel !)
= m~v + ~v m_
~ = m~a + m~
) F
_v
Wir unterscheiden zwei Flle:
Fall 1:
m = const
F~ = m~a
Fall 2:
~a = 0 ) ~v = const
~ = m~
) F
_v
Es wird immer mehr Masse aus der Ruhe auf eine Bestimmte Geschwindigkeit ~v gebracht.
)
m_ = 0
KAPITEL 1. MECHANIK
16
1.2.4 Kraft und Gegenkraft, Schwerelosigkeit
(Drittes Newtonsche Axiom)
Zu jeder Kraft wirkt eine Gegenkraft.
Wirkt auf einen K
rper eine Gegenkraft, so ist die relative Beschleunigung
Null.
Beispiel: Ein Mensch sitzt auf einem Stuhl.
Auf ihn wirken zwei Krfte:
F~0 = m~g und F~Stuhl = ;m~g =) Der Mensch bleibt in Ruhe.
Beispiel: freier Fall
Stein
mg
-mg
Erde
Zur Gewichtskraft wirkt auf den Stein keine Gegenkraft, daher fllt er.
1.2.5 Die quivalenz von schwerer und trger Masse
P F = m ~a (trge Masse)
i
i i
F~g = ms ~g (schwere Masse)
P
Ist ein K
rper nur seiner Gewichtskraft ausgesetzt, so gilt i = F~i = ms ~g
) ms ~g = mi~a
~a = mmst ~g
Beobachtung:
Ohne Luftwiderstand ist die Beschleunigung im freien Fall fr alle K
rper am selben
Ort gleich. mmst = const =: 1 =) quivalenz von ms und mt . =) Massenvergleich
ber die Gewichtskraft m
glich.
1.2.6 Reibungskrfte
Haft- und Gleitreibung
FH = H FN Haftreibungskraft
FGl = Gl FN Gleitreibungskraft
Diese Nherung ist unabhngig von Geschwindigkeit und Auageche.
1.3. DREHBEWEGUNG / ROTATION
17
.
FN
FN : Normalkraft = Kraft senkrecht (?) H : Haftreibungskonstante
Reibungsarbeit
WR = Gl FN s (Gleitreibung)
Bei Haftreibung tritt keine Reibungsarbeit auf, da s = 0 gilt.
Bestimmung von H an der schiefen Ebene
.
mg
FH
α
FN
FH = FN H
m g sin = m g cos H
sin = tan ) H = cos
1.3 Drehbewegung / Rotation
1.3.1 Kinematik der Drehbewegung
v(t)
v(t)
s
r
Ein Massenpunkt bewegt sich auf einem Kreis mit dem Radius r um den Mittelpunkt zunchst gleichf
rmig.
Eindimensional:
v(t) = ds
dt = s_ = const
Dreidimensional:
~v (t)
aber j~vj = const: die Richtung ndert sich!
Der Geschwindigkeitsvektor ist immer tangential zur Bahnkurve.
KAPITEL 1. MECHANIK
18
~v = j~vj ~etan ~etan : Einheitsvektor in Richtung der Tangente.
Da ~v = ~v(t) gilt, liegt eine beschleunigte Bewegung vor.
Radial- und Tangentialkomponente der Beschleunigung:
djvj ~e
~a(t) =
+ jvj d~edttan
dt tan
| {z }
| {z }
tangential (~atan =0 ) gleichfoermig
radial ~ar
etan
∆s
ϕ
r
Falls ' sehr klein ist, ist ~etan auf den Mittelpunkt gerichtet.
j~etanj
= rs ) d~edttan = limt!0 tsr = jrvj
j~etanj
| {z }
=0
) Radialbeschleunigung jar j = vr Die Kreisbewegung
schleunigung jar j in Richtung des Kreismittelpunktes.
2
hat eine konstante Be-
Beschreibung der Winkelgr
e ' im Bogenma: ' = rs ' : rad]
Die zeitliche nderung des Winkels ist die Winkelgeschwindigkeit:
;1
! = d'
!] = 1 rad
dt
s = 1s
fr die gleichf
rmige Kreisbewegung: ! = 2T =^ Kreisfrequenz,T = Umlaufzeit
Die Winkelgeschwindigkeit ist ein axialer Vektor: ~!
ω
v
.
..
r
v
;! ~
! steht senkrecht auf der Ebene der Kreisbewegung. ;! Die Drehrichtung
ist eine Rechtsschraube (Rechte-Hand-Regel).
Es gilt: ~v = ~! ~r (1)
Das Vektorprodukt zweier Vektoren ~a und ~b ist der Vektor ~c: ~c = ~a ~b
~c steht senkrecht zu ~a und ~b.
Fr seinen Betrag gilt: j~cj = j~ajj~bj sin <) (~a ! ~b)
~a ! ~b ! ~c bilden ein Rechtssystem.
Das Vektorprodukt ist weder kommutativ noch assoziativ:
(~a ~b) = ;(~b ~a)
1.3. DREHBEWEGUNG / ROTATION
19
~c (~a ~b) = (~c ~b)~a ; (~c ~a)~b
~v = ~! ~r
~r ~v = ~r (~! ~r)
= (~r ~r)~! ; (~
|r{z ~!}) ~r
=0
= r2~!
=) ~! = r12 ~r ~v
mit jar j = vr2
=) ~ar = ;!2~r Radialbeschleunigung
d2 '
Winkelbeschleunigung = dw
dt = dt2
Da gilt: dtd ! = dtd ( dtd ') und ! = d'
dt .
1.3.2 Scheinkrfte im gleichfrmig rotierenden Bezugssystem
z
ω
.A
z’
x’
y
x
y’
Scheinkrfte treten in beschleunigten Bezugssystemen auf, wobei in unserem
Beispiel die Drehachse z 0 parallel zu z ist.
ruhendes Bezugssystem:
(x! y! z) mit e^x ! e^y ! e^z (^ex ist Einheitsvektor in x-Richtung).
rotierendes Bezugssystem:
(x0! y0 ! z 0 ) mit e^0x ! e^0y e^0z .
Der Punkt A hat den Ortsvektor:
~r(t) = x(t)^ex + y(t)^ey + z(t)^ez ,
und die Geschwindigkeit:
dy
dz
~v (t) = dx
dt e^x + dt e^y + dt e^z ,
im rotierenden System dagegen:
~r(t) = x e^x + y e^y + z e^z
und die Geschwindigkeit:
~v (t) = d~dtr = dxdt e^x + dydt e^y + dzdt e^z
Ein ruhender Beobachter gibt die Geschwindigkeit im rotierenden System so an
(Rotation des Koordinatensystems wird bercksichtigt):
~v(t) = dxdt e^x + dydt e^y + dzdt e^z + (x e^x + y e^y + z e^z )
KAPITEL 1. MECHANIK
20
= ~v (t) + !~ ~r
und die Beschleunigung:
r
~a(t) = d~dtv = d~dtv + (~! d~
dt )
~a = ~a +
2(~
| v {z ~!}
+
~!| (~{z
r ~!})
Coriolisbeschleunigung Zentrifugalbeschleunigung
1.4 Arbeit, Leistung, Energie und Krfte
1.4.1 Arbeit
Konstante Kraft und geradliniger Weg
W := F s cos W] = F ]s]
= 1N 1m = 1Nm =: 1J
1J = 1Nm = 1 kgs2m m
Wir ziehen einen Wagen von links nach rechts:
F
α
.
|Fs | = |F| sinα
s
Wagen
|Fa | = |F| cos α
Fa = F cos Fa Kraftkomponente parallel zu ~s W = Fs cos = Fa s
Arbeit ist das Produkt aus Kraftkomponenten parallel zum zurckgelegten Weg
und dem Weg s selbst. F~ : auf den K
rper wirkende Zugkraft ~s : vom K
rper
zurckgelegter Weg
Vorzeichen:
gleiches Vorzeichen von Fjj und s :
verrichtet.
W > 0 =) Am K
rper wird Arbeit
unterschiedliche Vorzeichen von Fjj und s : W > 0
=) Der K
rper verrichtet Arbeit an seiner Umgebung, was im Gegensatz zum
Arbeitsbegri im Alltag steht.
Die Kraft abhngig vom geradlinigen Weg
F = F (s)
)
W = F s cos gilt hier nicht, da F nicht konstant ist.
Konzept: fr innitesimal kleine Wegpunkte ds ist die Kraft F konstant.
P
W = lims!0 F s cos Rs2
dW = F cos ds ) W = F(s) cos ds
s1
1.4. ARBEIT, LEISTUNG, ENERGIE UND KRFTE
Allgemeiner Fall: Dreidimensionale Bewegung
Idee: 0Zerlegung
1 der Kraft
0 Fin x-,1 y- und z- Komponente
dx
x
d~s = B
@ dy CA F~ =B
@ Fy CA
dz
Fz
Fx verrichtet nur eine Arbeit lngs d~x, nicht lngs d~y oder d~z, weil d~y! d~z?F~x.
Analog fr F~y und F~z =) dW = Fxdx + Fy dy + Fz dz
Skalarprodukt
Definition:
0a 1
x
~a =B
@ ay CA
az
~
~a b = ax bx + ay by + az bz
~a| 2{zR3} ~b| 2{zR3} ~a| ~b{z2 R}
0b 1
x
~b =B
@ by CA
bz
V ektor V ektor Skalarprodukt
Rechenregeln: (~a) ~b = (~a ~b) = ~a (~b) fr 2 R(Skalar)
Anwendung: dW = F d s cos dW = F~ d~s = Fx dx + Fy dy + Fz dz
Rs2
) W = F~ d~s
s1
1.4.2 Leistung und Wirkungsgrad
Arbeit: Parallelkomponente der Kraft mal Weg.
Leistung: Arbeit pro Zeit.
P = dW
Leistung
dt
(Spezialfall: fr P=const. gilt auch P = Wt )
P] = Wt]] = 1sJ = 1W
kg m m
kg m2
1W = 1 Js = 1 Nm
s = 1 s2 s = 1 s3
mechanische Leistung:
F~ d~s ~ d~s ~
P = dW
dt = dt = F dt = F ~v
P = F~ ~v = Fxvx + Fy vy + Fz vz
Wirkungsgrad (einer Maschine, Motor etc.):
Nutzleistung
= PPout
= investierte
Leistung
in
1.4.3 Potentielle Energie
Denition der Energie allgemein
Energie ist die Fhigkeit eines Systems, Arbeit zu verrichten.
Energie = gespeicherte Arbeit!
;! F] = W ] = 1J = 1Nm
Formen von Energie:
21
KAPITEL 1. MECHANIK
22
potentielle Energie (Energie der Lage / Federenergie)
kinetische Energie (Energie der Bewegung)
thermische Energie (Wrmeenergie)
chemische Energie (z.B. im Treibsto)
Strahlungsenergie (z.B. Licht)
potentielle Energie einer Hookschen Feder
F =Dx
(Feder entspannt fr x = 0)
Arbeit:
Rx
Rx
2
2
W = F(x) dx cos
| {z} = F(x) dx
x1
1 fuer F~ jj ~x
xR2
x1
xR2
W = Dx dx = D x dx
x1
x1
W = D ( x22 ; x21 )
2
2
Spezialfall:
x1 = 0
W = 12 D x2
Arbeit W zum Spannen der Feder = in der gespannten Feder gespeicherte Ener-
gie
Epot = 12 D x2 potentielle Energie einer Hookschen Feder
anschauliche Herleitung: W = mittlere Kraft Weg
W = D2x x = D2 x2
potentielle Energie im Gravitationsfeld
Annahme: g = const
Anheben um h
F = mg = const
s=h
cos = 1
) W = F s cos = mg h 1 = Epot
Epot = m g h
Beachte: Der Nullpunkt der potentiellen Energie im Gravitationsfeld ist willkrlich
festgelegt. Dies hat jedoch auf die Arbeit und damit die nderung Epot der
potentiellen Energie Epot keinen Einu.
1.4. ARBEIT, LEISTUNG, ENERGIE UND KRFTE
23
1.4.4 Kinetische Energie
An einem K
rper verrichtete Beschleunigungsarbeit resultiert in einem Zuwachs an
kinetischer Energie (Energie der Bewegung).
F = ma mitF~jj ~a ) cos = 1
= 12 a va22 = 2va2
s = 12 a t2 |{z}
v=at ) t= av
2
W = Fs cos
| {z} = ma v2a 1
=1
= 12 m v2
Ekin = 12 m v2
1.4.5 Der Energieerhaltungssatz (EES)
In einem abgeschlossenen System ist die Summe aller Energien konstant (Ein Erfahrungssatz).
Daher:
Energie kann weder aus dem Nichts erzeugt noch vernichtet werden, sondern immer
nur in andere Energieformen umgewandelt werden: Unm
glichkeit eines sogenannten Perpetuum Mobile.
EES der Mechanik (ein Spezialfall des allgemeinen EES)
In einem abgeschlossenen System ist die Summe aus potentieller und kinetischer Energie konstant, sofern ausschlielich konservative Krfte wirken:
Ekin + Epot = const
1.4.6 konservative und nicht konservative Krfte
Denitionen:
Bei konservativen Krften ist die verrichtete Arbeit unabhngig vom
Weg, der vom Startpunkt ~r1 zum Zielpunkt ~r2 verwendet wird. Die Gewichtskraft ist also eine konservative Kraft. Fr konservative Krfte lt sich jedem
Ort relativ zu einem Bezugspunkt eindeutig ein Potential (= pot. Energie
relativ zum Bezugspunkt) zuordnen.
Bei nicht-konservativen Krften ist die verrichtete Arbeit abhngig vom
Weg der von ~r1nach ~r2 verwendet wird. Die Reibungskraft ist also eine nichtkonservative Kraft.
1.4.7 Kraft und Potential
In einer Dimension:
dEpot = Fx dx
Fx = dEdxpot
KAPITEL 1. MECHANIK
24
In drei
1 (bei konservativen Krften):
0 Dimensionen
dEpot
dx
dEpot C
~
~ :Gradient (Vektor!)
r
dy A =: rEpot
dEpot
dz
Epot = Epot(x! y! z)
dEpot :potentielle Ableitung nach x (y, z werden dabei wie Konstanten
dx
F =B
@
schwereMasse = 1
traegeMasse
behandelt)
1.5 Schwingungen
1.5.1 Die harmonische Schwingung
Kreisbewegung von der Seite betrachtet (d.h. Projektion der Kreisbewegung auf
die y-Achse)
y
A
ϕ
A sinϕ
x
' =!t
: Winkel zum Zeitpunkt t = 0.
allg.: A(t) = A0 sin(!t + )
)sog. harmonische
Schwingung
| {z } A0: Amplitude
periodische Bewegung
!t + : Phase
!: Kreisfrequenz (! = 2T )
T: Periode
Wir setzen nun = 0 fr folgende berlegungen:
Ort: A(t) = A0 sin(!t)
_ = A0 ! cos(!t)
Geschwindigkeit: v(t) = A(t)
Beschleunigung: a(t) = v_ (t) = ;A0 !2 sin(!t)
2
=) Kraft: F(t) = m a(t) = ;
| m!
{z } A(t)
const:
Eine rcktreibende Kraft, deren Betrag proportional zur Auslenkung ist, fhrt zu
einer harmonischen Schwingung.
Eine solche Kraft heit elastische Kraft (Beispiel Hooksche Feder).
1.5. SCHWINGUNGEN
25
1.5.2 Die harmonische Schwingung einer Hookschen Feder
Feder, masselos
Gleichgewichtslage
bei y=0
0
Masse m
y(t) = y0 sin !t
a = y(t) = ;!2 y0 sin!t = ;!2 y(t)
F = m a = ;m !2 y (1)
F = ;Dy
(2)
(Hooksches Gesetz)
2
Aus(1)
q Dund (2) folgt D = m!
!= m
!: Kreisfrequenz
D: Federkonstante
m: Masse
1.5.3 Energieerhaltung bei einer harmonischen Schwingung
y = y0 sin !t
y_ = y0 ! cos !t
Epot = D2 y2 = D2 y02 sin2 !t
Ekin = m2 y_ 2 = m2 v02 !2 cos2 !t
= m2 y02 Dm cos2 !t
= D2 y02 cos2 !t
E = Epot + Ekin
= D2 y02 sin2 !t + D2 y02 cos2 !t
2
D
= D2 y02 |sin2 !t +
{z cos !t} = 2 y02
=1
E = Epot + Ekin = const
= D2 y02 = m2
2 2
y|{z}
0!
max: Geschwindigkeit
KAPITEL 1. MECHANIK
26
1.5.4 Das mathematische Pendel
ϕ
ϕ
|F |=mg sinα
.
mg
|FP|=mg cosα
rcktreibende Kraft: F? = ;m g sin '
Nherung fr kleine ' (' < 5 )
sin ' '
) F? = ;m g ' Elastische Kraft fr kleine '0
) harmonische Schwingung fr kleine '0
1.6 Impulserhaltung und Stogesetze
1.6.1 Der Impulserhaltungssatz
zur Erinnerung: ~p = m~v : Impuls
2. Newtonsche Axiom: F~ = ~p_
3. Newtonsche Axiom: F~1 = ;F~2 (jede Kraft hat eine Gegenkraft)
~ = F~1 + F~2 = 0 ) ~p_ = 0 ) p~ = const:
) F
(2 Massenpunkte in gegenseitiger Wechselwirkung)
allg.: Impulserhaltungssatz (IES)
Der Gesamtimpuls eines abgeschlossenen Systems ist konstant.
Ein abgeschlossenes System ist dabei ein System, auf das keine resultierende Kraft
von auen wirkt.
P
Gesamtimpuls: p~ = m1~v1 + m2~v2 : : : = i mi~vi
1.6.2 Der Schwerpunkt (oder Massenmittelpunkt)
P
~rs = Pmmi ~iri = m1m~r11 ++mm22 ~r+2:::+:::
d
~r_s = ~vs P
dt ~rs =P
= Pmmi ~vi i = P m~pii = mp~
~rs: Ort des Gesamtschwerpunktes
~ri: Ort des Einzelschwerpunktes
~vs: Schwerpunktgeschwindigkeit
p: Gesamtimpuls
m: Gesamtmasse
~p = m~vs
1.6. IMPULSERHALTUNG UND STOGESETZE
27
1.6.3 gerader, elastischer Sto
Gerader, zentraler Sto: Beide Massen bewegen sich auf einer Geraden.
Elastischer Sto: Der EES der Mechanik gilt, was bedeutet, da die gesamte
kinetische Energie vor und nach dem Sto gleich bleibt und keine Umwandlung von
kinetischer Energie in Wrme stattndet.
m1v1
m1v2
vor dem Sto: ~v1 ! ~v2
nach dem Sto: ~v10 ! ~v20
IES: m1~v1 + m2~v2 = m1~v10 + m2~v20
m1 (v1 ; v10 ) = m2 (v20 ; v2)
EES: 12 m1 v12 + 12 m2 v22 = 12 m1 v102 + v202
m1 (v12 ; v102 ) = m2 (v22 ; v202)
m1 (v1 + v10 )(v1 ; v10 ) = m2 (v20 + v2 )(v20 ; v2)
v1 ; v2 = ;(v10 ; v20 ) ()
() in IES eingesetzt:
v10 = (m1 ;mm21)+vm1 +22 m2 v2
v20 = (m2 ;mm11)+v2m+22 m1 v1
1. Spezialfall: m1 = m2 = m
v10 = v2 Geschwindigkeit, Impuls und Energie werden ausgetauscht.
v20 = v1
2. Spezialfall: m1 m2
m1
y
m2
v1 ; v2 = v20 ; v10
+v # ;v " v1 ; v2 = v ; (;v) = 2v
v = 2v v20 : ndert sich kaum bei Sto mit m1 .
1.6.4 gerader, zentraler inelastischer Sto
Der EES der Mechanik gilt nicht, da z.B. Energie durch Reibung oder unelastischer
Verformung entzogen wird.
IES: wie gehabt.
EES: E1 + E2 = E10 + E20 + W
KAPITEL 1. MECHANIK
28
1 m1 v2 + 1 m2 v2 = 1 m1 v02 + 1 m2 v02 + W
1 2
2 2
1
2
2
2
Falls W nicht bekannt ist, wird eine weitere Gleichung ben
tigt.
Gegeben: v1! v2 = 0! m1 = m2 = m
IES: m1 v1 + m2 v2 = (m1 + m2 ) v0
v0 = m1mv11 ++mm22 v2 = mm1 +1 vm1 2 = 2mm v1 = v21
vor dem Sto: Ekin = 12 m v12
0 = 2m v22 = 1 m v12
nach dem Sto: Ekin
2
4
1.6.5 nicht zentraler Sto mit m1 = m2
Kraftsto:
p
F = d~
dt
) d~
p = FR(t) dt
) ~
p = F(t) dt
mv1
α
mv1
mv’=v
1 a sinα
v2=va cos α
Stoßgerade
Keine Reibung zwischen den Kugeln!
=) Kraft ? Berhrungsche
=) Impulsbertrag ("Kraftsto) um jj Stogerade.
=) v20 jj Stogerade.
Kugel 2 erhlt wegen m1 = m2 den gesamten Impulsanteil jj Stogerade. Der
Impuls ? Stogerade ist nicht bertragbar und verbleibt daher bei Kugel 1.
~v102?~v202
fr m1 = m2
0
~v1: Geschwindigkeit der Kugel 1 nach dem Sto.
~v20 : Geschwindigkeit der Kugel 2 nach dem Sto.
1.7 Die Physik der Drehbewegung
1.7.1 Drehbewegung eines Massenpunktes
Bis jetzt hatten wir nur die Physik der Translationsbewegung, nun kommen wir
zur Physik der Kreisbewegung. Unser Ziel ist es, eine m
glichst bequeme Beschreibung ganz analog zur Translation zu nden. Als einfachstes System untersuchen
wir zunchst einen Massenpunkt auf einer festen Kreisbahn ohne Einwirkung der
Gravitation.
1.7. DIE PHYSIK DER DREHBEWEGUNG
29
Kinematik
Kinematik der Translation
s:
v = s_
a = v_ = s
Weg
Geschwindigkeit
Beschleunigung
Formeln fr a = const:
v = a t
a t2
s=p
2
v = 2as
Kinematik der Rotation
':
Winkel
! = ':_
Winkelgeschwindigkeit
= !_ = ':
Winkelbeschleunigung
Formeln fr = const:
! = !_ t
' = !2_ t2
p
! = 2!'
_
Umrechnung bei Kreisbewegung:
r
ds
dϕ
)
ds = r d'
ds = r d'
dt
dt
|{z}
|{z}
v
)
v = r!
!
1.7.2 kinetische Energie
kinetische Energie der Translation:
2
= 2pm
Ekin = 12 m v2 |{z}
p=mv
m: Masse
p: Impuls
kinetische Energie der Rotation
Ekin = 12 m v2 |{z}
= 12 m r2 !2 =: Ekin = 21 # !2
v=r!
#: Trgheitsmoment
#] = m]r2] = 1kg m2
Umformung:
)2 = L2
Ekin = 12 # !2 = (#!
2
#
2#
Ekin = L2#2
mit L := #!
L: Drehimpuls (vgl.: p = mv
2
L] = #]!] = 1 kgsm
$
L = #!)
1.7.3 Leistung
Leistung bei Translation:
F ds
P = dW
(falls F~ jj~v)
dt = dt = Fv
mit # = mr2
KAPITEL 1. MECHANIK
30
F: Kraft
v: Geschwindigkeit
Leistung bei Rotationsbewegung:
P = Fv = |{z}
Fr ! = M!
M
P = M ! mit M = F r wobei F~ ?~r
M: Drehmoment M] = F]r] = 1Nm
Vorsicht: trotz gleicher Einheit ist M weder eine Arbeit noch eine Energie!!!
1.7.4 Hebelgesetz
r1
ϕ
F1
dW = F2 ds = |{z}
F2 r d'
dW = M d'
M
mit M = |{z}
F2
r2
F2
r
|{z}
Kraft Hebelarm
Aus dem EES folgt:
F?r = const:
, F1r1 = F2r2
F1 = r2
) F
r1
2
1.7.5 Formulierung des 2. Newtonschen Gesetzes fr die
Drehbewegung
Die Tangentialkraft FT ist die tangential zur Kreisbahn wirkende Kraft.
FT = maT = mr!_
rFT = mr
|{z}2 !_
|{z}
M
r#
M = #!_
(vgl.: F = ma)
M: Drehmoment
#: Trgheitsmoment
)
1.7. DIE PHYSIK DER DREHBEWEGUNG
31
1.7.6 Gegenberstellung von Translation und Rotation
Translation
Gr
e, Formelzeichen
Weg
s! ds
Geschwindigkeit
~v = ds
dt
Beschleunigung
d2 s
~a = dv
dt = dt2
Masse
m
Kraft
F = m~a = dp
dt
Impuls
p = m~v
Kraftkonstante
c = Fs Arbeit
dW = F ds
Spannarbeit
W = 12 c s2
kinetische Energie
Ekintrans = 12 mv2
Leistung
P = dW
dt = Fv
Rotation
Einheit
Gr
e, Formelzeichen
m
Winkel
'! d'
m
Winkelgeschwindigkeit
s
~! = d'
dt
m2
Winkelbeschleunigung
s
d2 '
~ = d!
dt = dt2
kg
Massentrgheitsmoment
P
# = i mi ri2
kg sm2 = N
Drehmoment M~ = ~r F
M~ = #~ = dL
dt
kg ms = Ns
Drehimpuls
L~ = #~!
N
Winkelrichtgr
e
m
c = M' Nm = J = Ws Arbeit
dW = M d'
J
Spannarbeit
W = 12 c '2
J
kinetische Energie
Ekintrans = 12 #!2
W = Js
Leistung
~
P = dW
dt = M~!
Einheit
rad = 1
rad
s
= 1s
rad
s2
= s12
kg m2
Nm
kg ms2 = Nms
m2 = J
N rad
Nm = J = W s
N m rad2 = J
J
W = Js
1.7.7 Der Drehimpulserhaltungssatz
Drehimpuls L~ : Vektor mit Richtung jj zur Drehachse fr Massenpunkt. Die Richtung ergibt sich aus dem Umlaufsinn, der sich mit der Rechten-Hand-Regel! bestimmen lt.
L~ = ~r ~p = ~r (m~v )
L~ = #~!
Es gilt: Der gesamte Drehimpuls eines abgeschlossenen Systems (= Summe der Einzeldrehimpulse) ist konstant. Ein abgeschlossenes System
ist dabei ein System, auf das kein resultierendes ueres Drehmoment
~ ES )
wirkt. (Drehimpulserhaltungssatz, L
KAPITEL 1. MECHANIK
32
1.8 Die Mechanik starrer Krper
1.8.1 Trgheitsmoment ausgedehnter Krper
Trgheitsmomente sind immer bezglich einer bestimmten Achse deniert. Fr
verschiedene Drehachsen existieren verschiedene Trgheitsmomente.
Bis jetzt: Krper mit einem Massenpunkt
# = m r2
#: Trgheitsmoment
m: Masse
r: Abstand der Masse von der Drehachse
mehrere Massenpunkte mi
P
P
# = i #i = i mri2
Beispiel:
m1
r2
r1
Achse A1
m
2
Zeichenebene
Achse A || masseloser Stab
2
ausgedehnte Krper kontinuierlicher Massenverteilung
Integration
# = r2 dm = r2 %V
#: Beitrag von dm zu #
m
% = V : Dichte
V : Volumen
R
R r2 dV
# = r2R dm
=
%
R R r2(x! y! z) dx dy dz
=%
)
Einfache Beispiele:
Ring oder Hohlzylinder um eigene Achse
Scheibe oder Vollzylinder
r = const
R
R
# = r2 dm = r2 dm
# = mr2
Geringeres # als Hohlzylinder. Gleiche Masse und gleicher Radius gegenber
dem Hohlzylinder, da die Masse im Mittel! an der Drehachse liegt.
Methode: Aufsummierung der gleichen Volumenelemente mit gleichem Radius
als konzentrische Ringe.
1.8. DIE MECHANIK STARRER KRPER
dm = % dV = % U l dr
= % 2r
l dr r
r
R
R
# = r2 dm = r2 % 2r l dr
0
0
r
R
3
# = 2l% r dr
0
# = 2lg r44 ]r0
# = 2lg ( r44 ; 0)
2 2r2
1 2
# = r
| {zlg} 4 = 2 m r
=V %=m
Zylinder
dr
Homogener Stab (dnn), um seinen Schwerpunkt
L: Gesamtlnge des Stabes
%L := mL
RL
# = 2 #2 = 2 02 l2 dm
RL
# = 2 02 l2 %L dl
L
RL
# = 2%L 02 l2 dl = 2%L l33 ]02
# = 2%L 13 L83 = 121 %L L3
# = 121 m L2
Bei der
Rotation um
das Stabende:
R
R
L
L
2
# = 0 l dm = %L 0 l2 dl = %L l33 ]L0
# = %L L33 = 13 m L2
Kugel um den Mittelpunkt (homogene Vollkugel)
# = 25 m r2
1.8.2 Der Satz von Steiner
gegeben: #SP bezglich Achse ASP die durch den Schwerpunkt SP geht.
gesucht: # bezglich Achse A, die nicht durch SP geht, wobei A jj ASP .
33
KAPITEL 1. MECHANIK
34
Durchstoßpkt.
r SP
dm
a
A
SP
A SP
~rR= ~a + ~rSPR
# = r2 dm = (~a + ~rSP )2 dmZ
R
R
2 dm
= a2 dm + 2~a~rSP dm + rSP
| {z }
Z
#
SP
R
2
= a dm +2~a rSP dm + #SP
| {z }
=m
# = m a2 + #SP
Satz von Steiner
#SP : Trgheitsmoment bzgl. Achse durch SP
#: Trgheitsmoment durch neue Achse, die zu obiger parallel ist
a: Abstand der beiden Achsen
1.8.3 Zylinder auf schiefer Ebene
Drehachse ist die momentane Auageachse () a = r)
) # = #SP + mr2
(Satz von Steiner)
1
2
2
(Vollzylinder)
= 2 mr + mr
3
2
= 2 mr
(# = 2mr2 fr Hohlzylinder)
M = F?r = mgr sin '
M = #!_ ) !_ = M#
) a = rM
#
2
a = mgr32 mrsin2 ' = g sin32 '
a < g sin ' (;! Beschleunigung bei reibungslosem Gleiten)
1.8.4 Translation und Rotation rollender Krper
Beispiel: Der rollende Zylinder, Drehachse = Auageachse
Abstand Drehachse - Schwerpunkt: r
) # = #SP + mr2
(Satz von Steiner)
besser: vSP = !r (Geschwindigkeit des SP), sogenannte Rollbedingung (fr
Rollen ohne Schlupf)
Kinetische Energie:
2 mr2 2
Ekin = #2 !2 = #SP
2 ! + 2 !
1.8. DIE MECHANIK STARRER KRPER
Ekin
=
|{z}
Rollbeschleunigung
35
#SP !2 + m v2
2
2 SP
2
Ekin = 12 #SP !2 + 12 m vSP
Gesamte kinetische Energie = kinetische Energie der Rotation um den SP + kinetische Energie der Translation des SP
Allgemeine Bewegung: Translation des SP + Rotation um den SP
1.8.5 vektorielle Schreibweise bei Drehbewegungen
!~ : Vektor parallel Drehachse
Richtung gem Rechte-Hand-Regel j~!j = j'_ j
Drehimpuls:
L~ = ~r ~p
~ ? ~r
) L
~ ? ~p
^L
~ j = jrp sin j
^ jL
wobei: =<) (~r! ~p) (Zwischenwinkel zu ~r und p~)
L~ = #~!
Achtung: # ist nur in einfachen Fllen ein Skalar. Im Allgemeinen ist # ein sogenannter Tensor. Die Folge ist, da L~ ! !~ nicht automatisch parallel sind!
Jedoch: Fr jeden noch so komplizierten K
rper existieren 3 Achsen, die sogenannten Haupttrgheitsachsen fr die L~ jj ~! gilt. Fr symmetrische K
rper
entsprechen sie gerade den Symmetrieachsen, die aufeinander senkrecht stehen.
Drehmoment:
M~ = ~r F~
jF?j = F
sin '
r
F0
ϕ
F
F
F~ : zieht nur am Lager der Drehachse
M~ = L~ (aus dem 2. Newtonschen Gesetz)
1.8.6 Der Kreisel
Der krftefreie symmetrische Kreisel
Kreisel: Rotierender K
rper um festgelegte Drehachse
Symmetrischer Kreisel: Bei Verwendung eines K
rpers mit zwei gleichen Haupt-
KAPITEL 1. MECHANIK
36
trgheitsmomenten z.B. ein rotationssymmetrischer Kreisel.
Wirken auf einen Kreisel keine realen ueren Drehmomente, so ist
L~ = const (L~ ES) ein sog. Krftefreier Kreisel
.
Um einen krftefreien Kreisel auf der Erde beobachten zu k
nnen,darf die Gewichtskraft den Kreisel nicht mehr beeinussen. Daher lagern wir ihn auf eine punktf
rmige Auage in seinem Schwerpunkt. So bewirkt die Gewichtskraft kein Drehmoment
mehr.
Haupttrgheitsachsen durch den SP:
Achse mit gr
tem # : A1
Achse mit kleinstem # : A2
Achse senkrecht zu beiden: A3
Um A1 ! A2! A3 ist eine Rotation auch ohne ein Lager m
glich. Daher nennt
man sie Freie Achsen.
Nutation
Wenn ein Kreisel um eine seiner Haupttrgheitsachsen (freie Achsen) rotiert, dann
gilt ~! k L~ und aus L~ = const folgt, da ~! = const. So liegt eine stabile Rotation
um eine feste Drehachse (Fall 1) vor.
Bei einem Kreisel, der nicht um eine seiner Haupttrgheitsachsen rotiert (z.B. Fall
1 + seitl. Schlag auf die Drehachse), gilt ~! nicht k L~ . Da aber trotzdem L~ = const
(wegen M~ = 0) bewegen sich ~! und die Symmetrieachse (sog. Figurenachse) auf
Kegelmnteln um den ortsfesten L~ (Drehimpuls). Dies nennt man Nutation.
L~ = #~!
Nutationskegel
e
momentan
e
Drehachs
ω
DrehimpulsAchse
L
Figurena
chse
Drehmomente am Kreisel Przession
Es sei ~! k Haupttrgheitsachse (also keine Nutation!) und es sei M~ 6= 0.
Experiment: Man hnge ein rotierendes Rad, durch dessen Achse ein Stab fhrt,
an diesem Stab an ein Seil.
1.8. DIE MECHANIK STARRER KRPER
37
Seil
r
. M=r
. SP
x FG
L, ω
FG = m g
!~ k L~ L~ = #~!
M~ = ~r F~G
M~ =L~_ = ddtL~ ) dL~ = M~ dt
L~ k M~ M~ ? F~G
Daraus erkennen wir, da der Kreisel ? zur ausfhrenden Kraft wirkt. Dies nennt
man die Przessionsbewegung.
Dauer TP eines Przessionsumlaufs:
L
dL=M dt
R
1 Umlauf: dL = 2L
R dL = R M dt = M TRP dt = M T
0
2L = M T
TP = 2 ML
!P = T2P = ML = F~ r# !sinr '
1.8.7 Gleichgewicht am starren Krper
Statik: Was mu ich tun, damit ein K
rper im Zustand der Ruhe verbleibt ?!
P F~ = 0
i i
P
2. Vermeidung von Rotation um den SP ) M~ = 0
1. Vermeidung von Translation des SP )
i i
Im statischen Gleichgewicht ist sowohl die Summe aller an einem
Krper angreifenden Krfte als auch die Summe der auf ihn wirkenden
Drehmomente Null.
KAPITEL 1. MECHANIK
38
Arten von Gleichgewicht:
Stabiles Gleichgewicht
Der K
rper kehrt bei kleinen Auslenkungen aus der Ruhelage selbstndig in
diese zurck.
Beispiele:
Pendel
Indifferentes Gleichgewicht
Instabiles Gleichgewicht
Der K
rper verbleibt bei kleiner Auslenkung an einem Ort.
Beispiel: K
rper auf Ebene
Bei innitesimaler Auslenkung erhlt der K
rper eine Position und entfernt
sich um eine makroskope, endliche Auslenkung.
1.8.8 Hooksches Gesetz der Torsion, Drehschwingung
Bei der Torsion eines Drahtes oder dnnen Stabes ist das rckstellende Drehmoment proportional zum Verdrillungswinkel '.
M~ = ;D' ' Hooksches Gesetz der Torsion D' : Torsionsfederkonstante
Bei der Schwingung einer Torsionsfeder folgt aus dem Hookschen Gesetz ein elastisches Moment und eine harmonische Schwingung.
'(t) = '0 sin !t
'(t)
_ = '0 ! cos !t
'(t) = ;!2 '0 sin !t
(1) M = #'(t)
= ;#!2 '(t)
(2) M = ;D' '(t)
q
(1) ^ (2) ) #!2 = Dq' ) ! = D#'
(vgl.: bei Feder: ! = mD ).
1.9. GRAVITATION UND KEPLERSCHE GESETZE
39
1.9 Gravitation und Keplersche Gesetze
1.9.1 Das Newtonsche Gravitationsgesetz
Zwischen zwei Massen m1 und m2 wirkt eine anziehende Kraft, die zu m1 und m2
direkt und zum Quadrat ihres Abstandes indirekt proportional ist.
FG = ; mr1 2m2
Gravitationskonstante
= 6! 673 10;11 Nkgm22
Die Richtung von F~ ist antiparallel zu ~r.
Die Kraft FG auf die Probemasse mP im Einu der Masse M (z.B. die Erde):
FG = ;
r2M mP
Da FG = m g gilt g = ; rM2 , die Gravitationsfeldstrke, die an der Erdoberche
g = 9! 81 sm2 betrgt.
1.9.2 Feldstrke, Potential und potentielle Energie im Gravitationsfeld
Die Gravitationskraft ist eine konservative Kraft. Eine investierte Arbeit bewirkt
Epot.
dW |{z}
= F ds = + mr1 2m2 ds
sei F~ kd~s
Bewegung von m1 im Feld von m2 k zu ~r:
r
m1
m
Rr
2
Rr
2
2
W = F ds = m1 m2 r12 ds
r1
r1
W = ; m1 m2 ( r12 ; r11 ) = Epot
Vorzeichen:
r2 > r1
1
1
gr
erer Abstand = Zuwachs von Epot
r2 < r1
1
1
( r2 ; r1 ) < 0 ;( r12 ; r11 ) > 0
Da F eine konservative Kraft ist, ist Epot unabhngig vom Weg von ~r1 nach ~r2.
Epot ist maximal fr r ;! 1
Setze Epot = 0 fr r ;! 1 (neuer Bezugspunkt), dann ist:
Epot = ; mr1 m2
Dies nennt man die Bindungsenergie, mit der die Massen m1 und m2 aneinander
gebunden sind.
Denition des Gravitationspotentials ':
' = ; m
das Potential im Gravitationsfeld der Masse m.
r !
KAPITEL 1. MECHANIK
40
1.9.3 Bestimmung der Gravitationskonstanten Gravitationsdrehwaage nach Cavandish (1798):
Torsionsfaden
A
m1
m2
B’
Lichtzeiger
Spiegel
∆ϕ
m2
A’
2∆ϕ
m1
B
Kleine Kugeln an einem (beinahe) masselosen Stab an einem Torsionsfaden
q
drehbar. m1 und m2 bekannt. D' aus Schwingungsdauer: 2T = D#' .
Umlagerung der Massen m2
=) Kraft von m2 auf m1 wechselt Vorzeichen.
=) Drehmoment auf den Torsionsfaden wechselt Vorzeichen.
D' =
'
|{z}
Spiegeldrehung
= M =
2
|{z}
2
|{z}
V orzeichenwechsel 2 Kugelpaare
m1r2m2 2l cos '
Anwendung: Bestimmung der Masse der Erde:
g = mrEE ) mE = rE2 g
p
g: z.B. aus ! des mathematischen Pendels: ! = gl
: aus Gravitationsdrehwaage: rE 6370 km g = 9! 81 sm2
=) mE = 5! 97 1024kg
1.9.4 Planetenbahnen und Keplersche Gesetze
Von Johannes Kepler aufgrund empirischer Daten zur Planetenbewegung gefunden:
1. Keplersches Gesetz Die Planeten bewegen sich auf Ellipsen in deren einem
Brennpunkt die Sonne steht.
2. Keplersches Gesetz Der Radiusvektor Sonne-Planet berstreicht in gleichen Zeiten gleiche Flchen.
3. Keplersches Gesetz Die Quadrate der Umlaufzeiten verschiedener Planeten verhalten sich wie die Kuben der groen Bahnachsen.
Die Erklrung folgt aus dem Gravitationsgesetz und dem Drehimpulserhaltungssatz. So folgt das 2. Keplersche Gesetz direkt aus dem L~ ES und das 3. Keplersche
Gesetz aus dem Gravitationsgesetz, wobei hier die Gravitationskraft Zentralkraft
ist.
1.10. DEFORMATION FESTER KRPER
41
Spezialfall: Kreisbahn
mP rP !P2 = mSrP2mP
rP33 4T22 = mS
rP
mS
TP2 = 42 = const fr alle Planeten.
1.9.5 Gebundene und ungebundene Zustnde
Epot = ; m1rm2
E pot
Ept < 0 Epot
Gesamtenergie E:
E = Ekin + Epot
E = m22 v2 ; m1rm2
;!
0 fr r
r
;! 1
E 0 : m2 kann sich von m1 beliebig weit entfernen ! ungebundener Zustand
E < 0 : m2 kann sich nicht beliebig weit von m1 entfernen ! gebundener Zustand
Energie, um das Gravitationsfeld der Erde zu verlassen:
E0
m v 2 ; mE m 0
2
2 P
| {zrE}
g
vE2 2grE
p
Fluchtgeschwindigkeit: v 2grE = 11! 2 km
s
Satellitenbahnen
E < 0 : Ellipsen ;! gebunden (Spezialfall: Kreis)
E = 0 : Parabel ;! ungebunden
E > 0 : Hyperbel ;! ungebunden
1.10 Deformation fester Krper
1.10.1 Dehnung und Zugversuche
Bis jetzt haben wir alle K
rper als starre K
rper behandelt. In Wirklichkeit verndern jedoch feste K
rper ihre Form unter dem Einu von Krften.
Es gibt zwei Flle:
KAPITEL 1. MECHANIK
42
1. Elastische Verformung
Sie verschwindet, sobald die verformende Kraft weggenommen wird. ( Bsp.:
Hooksche Feder)
2. Plastische Verformung
Sie bleibt auch nach Wegfall der verformenden Kraft bestehen. (Bsp.: Blechschaden am Auto nach Unfall)
Spannungs-Dehnungs-Diagramm:
Kraft
Hooksches Gesetz
.
F
E
F
P
.
.
F
.
E
R
P
Längenänderung
Achtung! Der Verlauf der Kurve ist stark materialabhngig!
P: Proportionalittsgrenze
fr F < FP gilt: l F
E: Elastizittsgrenze
fr F < FE Dehnung reversibel
F: Festigkeitsgrenze
R: Reigrenze
1.10.2 Spannung, Dehnung und Hooksches Gesetz
Wir setzen voraus, da ein Faden unter Einwirkung einer Zugkraft gedehnt wird
und da die Kraft noch unterhalb der Proportionalittsgrenze liegt ) l F.
Wovon hngt l ab?
Von der Kraft (siehe oben)
Von der Fadenlnge
Jeder Faden der Lnge l dehnt sich um l
n Fden ) n l ( Serienschaltung!) ! l l
l
l
l
l
l
l
F
F
Serienschalung
Parallelschaltung
l
1.10. DEFORMATION FESTER KRPER
43
Vom Querschnitt
Parallelschaltung!
n Fden: auf jeden Faden wirkt nur noch FnG
) n-facher
Querschnitt: nl
Vom Material des Fadens
l = E1 Al F (1) (masseloser Faden !)
l: Fadenlnge
A: Querschnittsche
F : Zugkraft
E: sog. E-Modul oder Elastizittsmodul (hngt vom Material ab)
Definitionen:
" := l l relative Lngennderung oder Dehnung
:= AF Kraft pro Querschnittsche oder Zugspannung (bzw. bei Druckbelastung
Druckspannung)
Umformung von (1):
l = 1 F ) " = 1 " A
E
l
|{z}
|{z}
"
= E " Hooksches Gesetz
Die Spannung ist proportional zur Dehnung.
Wie verhlt sich ein Balken ?
)
gr. Dehnung
F
kl. Stauchung
Dehnung
Stauchung
neutrale Faser
F
1.10.3 Querkontraktion
Bei der Dehnung eines Fadens oder Stabes nimmt die Dichte in ? Richtung zur
Dehnung ab. Dies nennt man Querkontraktion.
d : relative Dickennderung
d
l : relative Lngennderung
l
d
= j dll j Poisson-Zahl
KAPITEL 1. MECHANIK
44
Volumennderung (quadrat. Querschnitt des Stabes)
V = (d ; d)2(l + d) ; d2l
= (d2 ; 2dd + d2)(l + l) ; d2l
d2l + d2l ; 2ddl ; 2ddl ; d2l
d2l ; 2dld
Das Produkt
zweier kleiner Gr
en ist vernachlssigbar klein.
V = d2 l ; 2dld
V
d2 l
d2 l
2
d
l
= l ; d
d
= l l (1 ; 2 dl l )
V = l (1 ; 2) = "(1 ; 2)
V
l
1.10.4 Kompressibilitt
V
= ;"(1 ; 2)
Druck lngs der x-, der y- und der z-Achse:
V =
V
+Vy + Vz
|{z}x
V
durch Druck in x;Richtg:
=) Isotroper Druck(von allen Seiten gleicher Druck)
V = ;3"(1 ; 2) = ;3 p (1 ; 2)
V
E
V = ;3 p (1 ; 2)
mit
" = Ep
V
E
Im Dreidimensionalen heit Kraft/Flche Druck: p = FA
Kompressibilitt V
= ; p
) = E3 (1 ; 2)
= K1
K heit Kompressionsmodul
V
1.10.5 Scherung und Torsion
Scherung
A
α
Die Kraft Fs wirkt tangential zur Flche A (Scherkraft) und bewirkt eine Scherung um den Winkel .
Scherspannung : := FAs
Es gilt: = G G : Torsions- oder auch Schermodul
1.10. DEFORMATION FESTER KRPER
45
Torsion eines dnnwandigen Rohres
ϕ
d
rϕ
l
α
dnnes Rohr:
Lnge l, Radius r, Torsionswinkel ', Wandstrke d r
Fr kleine Winkel gilt: tan ) = rl' (< 5 )
= G
F = A = |{z}
A G = 2r d G 2r d
= 2rd G r'l
= 2r2 d'l G
Drehmoment M: d ' )
M = Fr = 2r3 l G
D' = 2rl 3 d G
M = D' '
D' : Torsionskonstante eines dnnwandigen Rohres.
Torsion eines Stabes (kreisfrmiger Querschnitt)
Idee: Den Stab kann man als ineinandergeschachtelte dnne Rohre der Dicke d und
der Federkonstanten D' . Die Federkonstanten der einzelnen Rohre addieren
sich zu D' . Der Radius des Vollstabes sei R.
RA
D' = D'
R
RR
= 2rl dr G
0
RR
= 2 G r2 dr
2
l 0
= 2 Gl R44
D' = 2 Rl4 G
R4
D' : Torsionsfederkonstante eines Vollstabes mit kreisf
rmigem Querschnitt.
KAPITEL 1. MECHANIK
46
1.10.6 Elastische Energie und Energiequelle
Dehnung eines Stabes (oder Drahtes)
= "E
F = E l
A
l
F = ElA l
F=
D
l
|{z}
Federkonstante
9
>
= EA
D = l Federkonstante eines Stabes oder Drahtes.
>
Potentielle Energie
Arbeit beim Dehnen:
W = D2 (l)2 = E2lA l2 ll
= 12 E |{z}
A l ( ll )2 = 21 E V "2
V olumen V |
{z }
"
Energiedichte w (elastische Energie pro Volumen)
fr Dehnung.
w = WV = E2 "2
Analog herzuleiten fr Torsion:
w = G2 2
Energiedichte fr Torsion
1.11 Ruhende Flssigkeiten und Gase (Hydrostatik
und Aerostatik)
1.11.1 Druck in ruhenden Flssigkeiten (ohne Gravitation)
Flssigkeiten nehmen jede beliebige Form an. Es gibt keine Scherkrfte in ruhenden
Flssigkeiten.
Eine Flssigkeit bt auf Wnde den Druck p aus.
Kraft = F
p = Flaeche
A
p] = 1 mN2 = 1 pa
1 atm = 1! 013 105pa (1Atmosphre 1 bar)
Pascalsches Prinzip:
Der Druck in einem geschlossenen Gef ist ohne Gravitation an jedem
Ort innerhalb der Flssigkeit in allen Richtungen gleich.
Bemerkungen:
p ist kein Vektor. Da keine Scherkrfte existieren, bewirkt p eine Kraft, die senkrecht
auf der Oberche der Wand steht.
Anwendung ist z.B. die Hydraulik (z.B. Autobremsen)
F1 = A1
F2 A2
1.11. RUHENDE FLSSIGKEITEN UND GASE (HYDROSTATIK UND AEROSTATIK)47
F = p A1
F2= p A 2
1
Α1
Α2
p = const
1.11.2 Gravitation bei Flssigkeiten: der Schweredruck
p=p 0
h
A
Druck auf die Oberche der Flssigkeit: p0
(z.B. der Luftdruck von 1 atm = 105pa)
horizontale Flche A in der Tiefe h:
auf A wirkt p0
auf A wirkt zustzlich die Gewichtskraft der darberliegenden Flssigkeitssule.
F = p0 A + mg
= p0 A + %A |{z}
Vg
V =A h
%A : Dichte in H
he h
F = p0 A + %A h g A
p(h) = p0 +
%| A{zh g}
Schweredruck in der Tiefe h
1.11.3 Auftrieb Prinzip von Archimedes
Ein K
rper in einer Flssigkeit (oder einem Gas) erfhrt durch den Schweredruck
eine nach oben gerichtete Kraft, den sog. Auftrieb.
h1
h2 > h 1
48
Kraft von oben : F1 = (p0 + %A h1 g) A
Kraft von unten : F2 = (p0 + %A h2 g) A
F2 ; F1 = %A (h2 ; h1 )A g = %A V g = mg
FA = mA g
Prinzip von Archimedes
)
KAPITEL 1. MECHANIK
h2 > h1
)
F2 > F1
Kraft auf Krper in Flssigkeit
F~ = |{z}
F~A +
F~G
|{z}
nach oben nach unten
F = |{z}
%Fl V g ;
%K
|{z}
mFl
Masse des Koerpers
Vg
F = (%Fl ; %K ) V g
Flle:
1. %K < %Fl
)
FA > FG =) K
rper steigt auf, schwimmt
2. %K = %Fl
)
FA = FG =) K
rper schwebt
3. %K > %A
)
FA < FG =) K
rper sinkt
Die Folge davon ist, da ein schwimmender K
rper so tief eintaucht, bis das
Gewicht der verdrngten Flssigkeit dem Gewicht des K
rpers gleich ist.
1.11.4 p(h) bei Gasen: die barometrische Hhenformel
Die Dichte % bei Gasen hngt vom Druck ab:
% p! d.h. %p = p%00 = const
fr T = const (T : Temperatur)
%0 : Dichte an der Erdoberche
p0: Druck an der Erdoberche
Drucknderung dp von dh abhngig:
dp = ;% g dh = % p %p00
dp = ;p %p00 g dh
pR(h)
dp
p0 p
Rh
= ; p%00 g dh
0
lnp ; lnp0 = ln pp0 = ; %p00 g h
p
%0
p0 = exp p0 g h]
p = p0 exp(; %p0g h)
Barometrische Hhenformel
1.11. RUHENDE FLSSIGKEITEN UND GASE (HYDROSTATIK UND AEROSTATIK)49
Druck in Flüssigkeiten:
h
0m
p
0,3 bar
Druck in Gasen:
nimmt exponentiell mit der Höhe ab
h
1 bar
p
1.11.5 Oberchenspannung und Kapillaritt
Aufgrund von anziehenden Krften zwischen den Moleklen einer Flssigkeit ben
tigt man die Energie dE, um eine Oberche um dA zu vergr
ern.
dE = dA : Oberchenspannung
dx
F
Flüssigkeitslamelle
l
Filmwaage
bewegliche Barriere mit dem Umfang U
Barriere mit Umfang U:9F = U FG = mg
dE =
2
l dx >
=
|{z}
F = 2 l Die Rckstellkraft ist unabh. von A
2 Oberflaechen
>
dE = F dx
Druck in Flssigkeitskugel
Oberchenenergie: W = 4r
|{z}2 A
dW
dr
= 42r dW = 8r dr (1)
andererseits dW = F dr
dW = p 4r2 dr (2)
(1) = (2) : p 4r2 dr = 2 4r dr
) p = 2r
Folgen:
Tr
pfchenbildung
KAPITEL 1. MECHANIK
50
Vereinigung von Tr
pfchen
Regen
Hpfen von Hg-Tr
pfchen (groes )
Druck in einer Seifenblase
p = 3r
, da 2 Oberchen
Kapillaritt und Grenzchenspannung
Kapillaraszension
Kapillardepression
h
h
H2O
Hg
Erzeugung von zustzlicher Grenzche
setzt Energie frei
erfordert Energie
Gleichgewicht
2 = % h p
r
Kapillardruck
Schweredruck
1.12 Strmende Flssigkeiten und Gase (Hydrodynamik und Aerodynamik)
1.12.1 Die Kontinuittsgleichung (inkompressible Strmung)
A1
A2
Die sog. Flulinien verlaufen an jeder Stelle parallel zum Geschw.vektor ~v.
stationre Strmung: ~v hngt nur vom ~r (Ort) ab und nicht von der Zeit.
=) Stromlinien stimmen mit den Strombahnen berein
1.12. STRMENDE FLSSIGKEITEN UND GASE (HYDRODYNAMIK UND AERODYNAMIK)51
inkompressible Strmung: Dichte % ist konstant. Es gibt sie bei Flssigkeiten
und langsam str
menden Gasen.
Verengung eines Rohres:
Pro Zeiteinheit mu durch jeden Querschnitt des Rohres die gleiche Masse str
men.
Daher mu das Medium bei A2 (Verengung) schneller als bei A1 str
men.
dm1 = % dv1 = % A1 dx1 = %1 A1 v1
dt
dt
dt
dm2 = % dv2 = % A2 dx2 = %2 A2 v2
dt
dt
dt
dm1 = dm2 ) %1 A1 v1 = %2 A2 v2
dt
dt
Speziell fr inkompressible Medien (% = const):
A1 v1 = A2 v2
Kontinuittsgleichung
1.12.2 Potentielle und kinet. Energie in strmenden Medien:
die Bernoulli-Gleichung
A1v1 = A2 v2
) v ndert sich mit A
) Ekin ndert sich mit A
Woher kommt und wohin geht die zustzliche kinet. Energie ?
p1
p2
p3
kein Kapillareffekt !
Durch Unterschiede im statischen Druck ndert sich zugleich die potentielle
Energie des Mediums.
F 1 =A1 p1
F2 = A2 p 2
dW1 = p1 A
| 1{zdx1}
dV1
dW2 = F2 dx2 = p2 A
| 2{zdx2}
dV2
% = const
) dV1 = dV2 =: dV
(1) dW = dW1 ; dW2 = (p1 ; p2)dV = dm
% (p1 ; p2 )
Wenn wir annehmen, da keine Reibung entsteht und da eine ideale! oder reibungsfreie Str
mung vorliegt, k
nnen wir feststellen, da die Arbeit dW zu einer
nderung der kinet. Energie Ekin fhrt.
KAPITEL 1. MECHANIK
52
(2)
dW = dEkin = dm2 2 v22 ; dm2 1 v12
dm (v2 ; v2 )
=
1
2 2
|{z}
dm1 =dm2 =dm
(1) = (2)
% v2 +
2 1
|{z}
dm
2
2
) dm
2 (v2 ; v1 ) = % (p1 ; p2)
p1
|{z}
Staudruck statischer Druck
= %2 v22 + p2 =:
Bernoulli-Gleichung
p0
|{z}
Gesamtdruck
Gesamtdruck = statischer Druck bei v = 0
v 6= 0 ) stat. Druck < Gesamtdruck
Im Gravitationsfall (zustzlich Schweredruck):
p1 + %2 v2 + %hg = p0 = const
% v2 : Staudruck %hg: Schweredruck p0: Gesamtdruck
2
Druckmessung
a) statischer Druck:
Messöffnung
pStau
B) Gesamtdruck: sog. Pitol-Rohr
p Stau
c) dynamischer Druck: sog. Prandelsches Staurohr
Dierenz aus Gesamtdruck und stat. Druck. Aus pStau v2 folgt Geschw.messung.
p Stau
1.12. STRMENDE FLSSIGKEITEN UND GASE (HYDRODYNAMIK UND AERODYNAMIK)53
1.12.3 Viskose Strmung zwischen Platten
Bislang haben wir die Reibung vernachlssigt. Ab jetzt betrachten wir Str
mungen
mit Reibung, d.h. viskose Strmungen. Einfachster Fall: zwei gegeneinander
bewegte Platten, deren Spalt mit #l, Luft etc. gefllt ist.
Platte 2; vx = v
v
Platte 1; v=0
Die Flssigkeitsschichten gleiten aneinander vorbei, wodurch Reibung entsteht.
Die unterste Flssigkeits- oder Gasschicht haftet an Platte 1, die oberste an Platte
2. v nimmt von Platt1 nach Platte 2 zu.
Kraft, um Platte 2 mit v zu bewegen:
dv
F = A dx
Newtonsches Reibungsgesetz
: Viskositt ( Zhigkeit!) ] = 1 mNs2
A: Flche der Platte
1.12.4 Laminare Strmung durch Rohre das Gesetz von HagenPoiseuille
In einem starken Rohr mit dem Radius R betrachten wir ein Strohmr
hrchen mit
dem Radius r.
p
2
A=r π
l
p
F = r2(p1 ; p2)
Antriebskraft!
dv
F = A dv
Reibungskraft
dr = 2r l dr
dv
2
) r (p1 ; p2) = 2r l dr
p1 ;p2 RR r dr = R0 dv
2l
0
v
) v(r) = p14;lp2 (R2 ; r2)
Geschwindigkeit
Parabolisches Geschwindigkeitsprofil im Rohr:
KAPITEL 1. MECHANIK
54
v(r)
Parabel
r
+R
-R
_ bestimmen wir durch einen Zylinderring mit Radius
Die Massenstromstrke (M)
r und der Dicke dr . Dann fhren wir eine Integration ber die Zylinderringe aus.
R
V_ = % R 2rdr dx
=
%
M_ = dm
dt
dt
| {z } dt
0
RR
A
= % 2r dr v(r)
0
RR
= % p14;lp2 2 r(R2 ; r2) dr
0
RR
%
= 2l (p1 ; p2 ) (rR2 ; r3) dr
0
M_ = 8%l (p1 ; p2 ) R4
Gesetz
M_ R4
von Hagen-Poiseuille
1.12.5 Stokesche Reibung einer Kugel
Eine Kugel in #l hat eine konstante Sinkgeschwindigkeit. Daraus kann man eine
Abschtzung der Reibungskraft FR gewinnen.
dv
FR = A dx
2
v = 4 r v
FR 4r
r
|{z}
Kugeloberflaeche
genaue Untersuchungen zeigen:
FR = 6 r v
Stokesches Gesetz fr Kugel
Gleichgewicht: d.h. v = const fr
m g ; jFAj = 6 r v
(Bestimmung von )
1.12.6 Turbulente Strmung und Reynolds-Zahl
Laminare Strmung: Stromlinien
turbulente Strmung: Wirbelbildung Falls die Reynoldszahl einen bestimmten
Grenzwert berschreitet (z.B. 2300 bei Rohrstr
mung), ndet ein Umschlag
von laminar in turbulent statt.
Re = %L v
Re] = 1 ( dimensionslose Zahl!)
v: ab dieser Geschwindigkeit ndet der Umschlag statt
L: charakt. Lnge eines Systems
1.12. STRMENDE FLSSIGKEITEN UND GASE (HYDRODYNAMIK UND AERODYNAMIK)55
1.12.7 Luftwiderstand und cw -Wert
Wir betrachten ein Fahrzeug mit der Querschnittsche A und nehmen an, da
das gesamte vom Fahrzeug verdrngte Luftvolumen auf Fahrzeuggeschwindigkeit v
beschleunigt wird.
dW = F ds = F v dt
2 v2
A
ds
dW = dEkinLuft = dm
2 v = 2%
|{z}
v2 % A v dt
V olumen der Luft
F v dt = 2
F = 2% v2 A
Je nach Formgebung ist F gr
er oder kleiner:
F = cw %2 v2 A cw : sog. cw -Wert
Leistung: P = F v = cw %2 v3 A
Dies bedeutet:
doppelte Endgeschwindigkeit ) 4-facher Energieverbrauch
stung.
)
)
8-fache Motorlei-
56
KAPITEL 1. MECHANIK
Kapitel 2
Schwingungen
Ein physikalischer Vorgang, bei dem sich eine Megr
e periodisch ndert, heit
Schwingung . In Physik und Technik sind Schwingungen von enormer Bedeutung,
da sich viele Vorgnge durch sie beschreiben lassen. An eine Gleichgewichtslage gebundene Teilchen benden sich in einem Potentialminimum. Daher kann das Potential in ihrer Umgebung als Parabel angenhert werden, wodurch sich V (x) 21 kx2
ergibt. Das fhrt zu einer elastischen Kraft F (x) = dV
dx = ;kx . Ein Teilchen, da
einer derartigen Kraft ausgesetzt ist, schwingt harmonisch und sinusf
rmig. Jedoch
fhrt ein Teilchen meist nicht nur eine Schwingung aus, sondern mehrere. Diese
k
nnen sich hinsichtlich Amplitude, Frequenz, Richtung und Phase unterscheiden.
57
KAPITEL 2. SCHWINGUNGEN
58
2.1 Freie und erzwungene Schwingungen
2.1.1 Schwingungsarten
Harmonische Schwingungen Sinusf
rmig und zeitabhngig
freie Schwingung (ohne ueren Erreger)
ungedmpfte Schwingung
Inharmonische Schwingung erzwungene Schwingung (mit periodischem uerem Erreger)
gedmpfte Schwingung, das heit: Energie wird abgefhrt (zum Beispiel durch
Reibung)
2.1.2 Die Bewegungsgleichung
In Vektorschreibweise
In einer Dimension
m~a =
ma =
X~
Fi
X
Fi
Als Beispiel die Bewegungsgleichung der Hook'schen Feder (ohne Gravitation)
mx + Dx = 0
Diese Schreibweise von F = ma beschreibt das physikalische Verhalten der Feder
vollstndig. Es handelt sich hierbei um eine Dierentialgleichung.
2.1.3 Dierentialgleichungen
Gleichungen, die neben einer Funktion auch deren Ableitung enthalten, heien Differentialgleichungen.
v = at , s_ = st
Hat man eine Dierentialgleichung, zum Beispiel die Bewegungsgleichung, so sucht
man die Menge aller Funktionen, die diese Dierentialgleichung l
sen: Die %allgemeine L
sung der Dierentialgleichung. Jede Funktion, die man in die Dierentialgleichung einsetzen kann und die diese erfllt, heit eine %spezielle L
sung
der Dierentialgleichung. Da eine Funktion tatschlich L
sung einer bestimmten
Dierentialgleichung ist, zeigt man durch Einsetzen1 dieser Funktion in die Differentialgleichung. Sucht man die L
sung einer Dierentialgleichung, macht man
einen Ansatz, das heit, man denkt sich eine Funktion aus, von der man vermutet,
da sie die Dierentialgleichung l
t. Wenn dies nicht der Fall ist, mu man weiter
probieren.
1 Einen
eleganteren Beweis gibt es nicht.
2.1. FREIE UND ERZWUNGENE SCHWINGUNGEN
59
2.1.4 Der harmonische Oszillator
Die Hook'sche Feder (ohne Gravitation)
a) Bewegungsgleichung mx + Dx = 0
b) Ansatz x(t) = c1 cos !0t + c2 sin !0t ) x(t) : : :
eingesetzt in a) liefert:
q
c) Kreisfrequenz !0 = mD
das heit, fr c) erfllt der Ansatz die Dierentialgleichung, egal wie c1 , c2 gewhlt
sind! Daher stellt b) die allgemeine L
sung der Dierentialgleichung a) dar. Jedes
Wertepaar (c1 ! c2) liefert eine spezielle L
sung von a) . Wie erhalte ich nun aus der
allgemeinen L
sung eine fr mein System gltige L
sung? Indem die Anfangsbedingungen eingesetzt werden:
x(t = 0) = : : :
x(t
_ = 0) = : : :
Die Anfangsbedingungen legen die Koe&zienten c1 und c2 eindeutig fest.
x(t = 0) x0 = c1
x(t = 0) v0 = c2 !0
wir erhalten die spezielle L
sung:
x(t) = x0 cos !0t + !v00 sin !0t
Das ist die Gleichung des harmonischen Oszillators .
2.1.5 Gegenberstellung verschiedener
harmonischer Schwingungen
Bei diesen freien, ungedmpften Schwingungsarten wird periodisch die Energie zwischen kinetischem und potentiellem Zustand umgewandelt, das heit, es gilt:
Ekin + Epot = Eges = const
Fr Linearbewegungen, wie bei Schwingung a) und c), gilt:
ma+ 'Betrag der Rckstellkraft] = 0
Bei Drehbewegungen, Fall b) und d), gilt entsprechend:
#'+ 'Betrag des rckstellenden Drehmoments] = 0
a) Hooksche Feder
r
2
mx + Dx = 0 =) !0 = D
m = T = 2
b) Drehschwingung
r
#' + D' ' = 0 =) !0 = Dx
#
c) mathemathisches Pendel (Nherung fr kleine Auslenkungen)
ml' + mg' = 0 =) !0 =
rg
l
KAPITEL 2. SCHWINGUNGEN
60
d) physikalisches Pendel (Nherung fr kleine Auslenkungen)
r
#' + mgS' = 0 =) !0 = mgS
#
S stellt den Abstand zwischen Schwerpunkt und Drehpunkt dar.
2.1.6 Der freie, gedmpfte Oszillator
Hug ist die Reibungskraft FR proportional zur Geschwindigkeit, wie zum Beispiel
bei der Stokes-Formel: FR = ;6vr. Daher fhren wir FR = ; x_ ; Dx in die
Bewegungsgleichung ein: ma = ;v ; Dx mit = 6r.
mx + x_ + Dx = 0
Wobei x_ die Reibung und mx + Dx die Hook'sche Feder darstellt.
Als Abkrzung benutzt man
r
!0 := D
m
:= 2m
=) y + 2 y_ + !02 y = 0 Die L
sung dieser Dierentialgleichung fhrt zu
y = y0 e;t sin
q
!02 ; 2 t + '0
wobei hierbei mit der e- Funktion die exponentiell mit der Zeit t abklingende Amplitude
mit der sin - Funktion die Schwingung mit der Kreisfrequenz ! =
p 2 und
2
!0 ; dargestellt wird. Aus den Anfangsbedingungen ergibt sich y0 fr die
Amplitude und '0 fr die Phase bei t = 0 .
Wir unterscheiden drei Flle der gedmpften Schwingung:
a) Schwingfall ! > 0
2.1. FREIE UND ERZWUNGENE SCHWINGUNGEN
61
b) aperiodischer Grenzfall ! = 0
c) Kriechfall ! ist imaginr, da !02 ; 2 < 0
Die Gleichgewichtslage wird bei Fall b) am schnellsten erreicht. Dies ist bei
Zeigermeinstrumenten von Bedeutung.
KAPITEL 2. SCHWINGUNGEN
62
2.1.7 Erzwungene Schwingungen und Resonanz
Erzwungene Schwingungen werden durch eine periodische, anregende Kraft der Frequenz ! erzeugt.
L(t) = L0 sin(!t)
Fext(t) = DL(t) = DL0 sin(!t)
Bewegungsgleichung:
qD
mx + x_ + Dx = DL0 sin(!t)
Mit !0 = m = 2m folgt:
x + 2 x_ + !02 (x ; L0 sin(!t) = 0
Der Ansatz zur L
sung dieser Dierentialgleichung lautet x = x0 sin(!t ; '). Eingesetzt in die Dierentialgleichung ergibt sich folgende L
sung (Rechengang ist etwas
langwierig, deshalb wird hier darauf verzichtet.) :
!02
x0 = p
L0
(!02 ; !2 )2 ; (2!)2
x0 Amplitude der Schwingung
L0 Amplitude des Erregers
!0 Eigenfrequenz der Schwingung
! Frequenz des Erregers
Dmpfung
' Phasenwinkel
tan ' = 2 !02 ;! !2 wirkliche Amplitude
x0
L0
1
ω/ω 0
1
2.2. BERLAGERUNG VON SCHWINGUNGEN
63
ϕ
π
π /2
ω/ω 0
1
Wir unterscheiden drei Flle der Erregung:
a) Erregerfrequenz ist Null ! = 0
x0 = L0 ' = 0 Die Schwingung hat die gleiche Amplitude und Phase, wie der
Erreger.
b) Erreger- 2und Eigenfrequenz sind gleich ! = !0
x0 = L0 2!!0 ' = 2
c) Erregerfrequenz ist bedeutend hher ! ! 1
x0 ! 0 ' ! Die Amplitude geht gegen 0 und ist gegenphasig zum Erreger.
Das Phnomen, da die Amplitude der Schwingung nahe !0 sehr gro wird, heit
Resonanz.
p2 2
x0
L0 ist die Resonanzberh
hung !max = !0 ; 2 ist die Resonanzfrequenz, die
mit gr
erer Dmpfung abnimmt.
2.1.8 Einschwingvorgnge
Da fr das L
sen von linearen Dierentialgleichungen gilt, da die allgemeine L
sung
der inhomogenen Dierentialgleichung gleich die allgemeine L
sung der zugeh
rigen homogenen Dierentialgleichung addiert mit einer L
sung der inhomogenen
Dierentialgleichung ist, k
nnen wir fr Einschwingvorgnge die folgende Formel
aufstellen:
x(t) = e;t (c1 cos (!frei t) + c2 sin (!frei t)) + A cos (!err t ; ')
mit der Kreisfrequenz !frei des freien Oszillators und der Erregerfrequenz !err .
2.2 berlagerung von Schwingungen
2.2.1 berlagerung paralleler Schwingungen
Diese Schwingungsarten treen wir in der Musik an, zum Beispiel bei Klavier und
Geige.
64
KAPITEL 2. SCHWINGUNGEN
berlagerung zweier homogener Teilschwingungen
x(t) = A1 cos(!1 t ; '1) + A2 cos(!2 t ; '2 )
Whle Zeitpunkt t1 so, da '1 = 0 gilt, dann lautet die Bewegungsgleichung x(t) =
A1 cos(!1t) + A2 cos(!2 t ; '), wobei A Die Amplitude und ! die Kreisfrequenz
darstellt. Wir k
nnen nun fr diese Gleichung verschiedene Flle unterscheiden.
a) Gleiche Frequenzen !1 = !2 = !
x (t) = A1 cos (!t) + A2 cos (!t ; ')
Laut Formelsammlung(SinusCosinusstze) ist dies jedoch gerade x(t) = A cos (!t ; 'ges )
p
') . Also k
nnen
2
mit A = A1 + 2A1 A2 cos (') + A22 und tan ('ges) = A1A+2Asin(
2 cos(')
wir sagen: Die berlagerung von zwei oder mehreren harmonischen Schwingungen
gleicher Frequenz ergibt gerade wieder eine harmonische Schwingung dieser Frequenz.
b) Unterschiedliche Frequenzen !1 6= !2
Als Resultat bekommen wir in diesem Fall durch berlagerung eine unharmonische
Schwingung. Falls mn rational ist, das heit, es gilt m!1 = n!2 mit m! n 2 N , dann
erhalten wir als Periodendauer T m!1 = n!2 () nT1 = mT2 = T .
c) Fast gleiche Frequenzen !1 !2
; ; Laut Formelsammlung gilt: cos x + cos y = 2 cos x;2 y cos x+2 y .
Folglich gilt fr uns:
;
;
A cos (!1t) + A cos (!2t) = 2A cos !2 ;2 !1 t cos !2 +2 !1 t .
Fr !1 = !2 mit ! = !2 ; !1 ergibt sich dann
; A cos (!1t) + A cos (!2t) = 2A cos 2! t cos (!t)
;
Die zeitliche Variation der Amplitude wird durch A(t) = 2A cos 2!t ausgedrckt. Die Periode T der Schwebung entspricht dem zeitlichen Abstand benachbarter Minima des obigen Cosinus. =) !T
2 = . Eine Schwebung ist daher eine
Amplitudenmodulation mit der Dierenzfrequenz ! . Wenn beide Amplituden
den selben Wert haben, ist dies eine reine Schwebung mit vollstndiger Ausl
schung im Minimum. Sind die Amplituden jedoch verschieden, dann erhalten wir
eine unreine Schwebung mit A = jA2 ; A1 j > 0 im Minimum.
2.2. BERLAGERUNG VON SCHWINGUNGEN
65
2.2.2 berlagerung orthogonaler Schwingungen
Der besseren bersichtlichkeit wegen betrachten wir den Fall zweier harmonischer
Schwingungen ohne Reibung (Dmpfung), die zueinander senkrecht stehen.
Wir unterscheiden fnf Flle, die bei dieser Kombination auftreten k
nnen.
w1 Schwingungsfrequenz des ersten Schwingers
w2 Schwingungsfrequenz des zweiten Schwingers
' Phasenverschiebung
a) !1 = !2 = ! und ' = 0
Mit x = A cos(!t) und y = B cos(!t) ergibt sich Ax = By
Es gilt daher: y(x) = BA x , also eine Gerade in unserem Bild.
Allgemein gilt: ' = n mit n 2 Z =) y(x) =Gerade.
b) !1 = !2 = ! , ' = 2 und A = B
Durch den Phasenunterschied und A = B ergibt sich eine Kreisbahn.
Allgemein gilt: ' = (2n ; 1) 2 mit A = B und n 2 Z =) y(x) =Kreisbahn.
66
KAPITEL 2. SCHWINGUNGEN
c) !1 = !2 = ! und A! B! ' nicht speziell
Allgemein gilt: !1 = !2 =) y(x) =Eliptische Bahn.
d) !!12 ist rational () m!1 = n!2 mit m! n 2 N
Nach der Zeit mT2 = nT1 ist der Anfangszustand in x und y wieder erreicht. Wir
erhalten eine geschlossene Bahn, eine sogenannte Lissajous Figur.
Allgemein gilt: m!1 = n!2 mit m! n 2 N =) y(x) =Lissajous Figur.
2.2. BERLAGERUNG VON SCHWINGUNGEN
67
e) !!12 nicht rational
Es ergeben sich keine geschlossenen Bahnen.
2.2.3 Fourier-Synthese und Fourier-Analyse
Fourier-Synthese
Beliebige periodische Funktionen mit der Periode T = 2! sind als Summen von
Sinusfunktionen mit ganzzahligen Vielfachen der Grundfrequenz ! darstellbar:
y(t) = y0 +
X
yn sin(n!t + 'n)
Fourier-Analyse
Umgekehrt kann man natrlich auch jede beliebige periodische Funktion in Sinusfunktionen zerlegen. Die Umformung obiger Funktion nach der Formelsammlung
ergibt:
X
X
y(t) = y0 + an cos(n!t) + bn sin(n!t)
wobei gilt:
yn2 = a2n + b2n mit den Fourierkoe&zienten
R
R
T
2
an = T 0 y(t) cos(n!t)dt und bn = T2 0T y(t) sin(n!t)dt
1! ist die Grundschwingung.
2! die erste Oberschwingung, also die zweite Harmonische. . . . n! die (n ; 1)-te
Oberschwingung, also die n-te Harmonische.
Als Beispiel hier nun eine Rechteckfunktion
Y
t
und das dazugeh
rige Fourierspektrum
yn
1
2
3
4
5
6
7
2.2.4 Gekoppelte Schwingungen
Die gekoppelte Federschwingung
Harmonische
KAPITEL 2. SCHWINGUNGEN
68
D
D12
m
D
m
q
Hierbei sind zwei harmonische Oszillatoren mit der Frequenz ! = mD durch
eine Feder mit der Federkonstanten D12 gekoppelt. Durch diese Kopplung wird der
Austausch von Energie zwischen beiden Oszillatoren erm
glicht. Wir unterscheiden
zwei Fundamentalschwingungen, bei denen kein Energieaustausch stattndet.
a) gleichphasige Schwingung
q
Die Kopplungsfeder ist immer entspannt. Es gilt: !1 = mD = !0
D
m
D m
D12
D12
m
m D
D
b) gegenphasige Schwingung
Der Mittelpunkt der Kopplungsfeder bleibt fest. Jede Seite hat eine Hlfte der
Kopplungsfeder,
Lnge,
q D+2D12 also
q Ddie halbe
q 2 daherD12die zweifache Federkonstante.
D
12
!2 =
m = m + 2 m = !0 + 2 m
D
m D12 m
D
2.2. BERLAGERUNG VON SCHWINGUNGEN
D m
D12
69
m D
Jede beliebige Schwingung des Systems lt sich als berlagerung der beiden
Fundamentalschwingungen darstellen.
Spezialfall Schwache Kopplung:
Wenn D12 wesentlich kleiner als D ist, gilt !1 ' !2. Daher fhrt eine berlagerung
von !1 und !2 zu einer Schwebung mit der Frequenz ! = !2 ; !1. Die Energie
im System schwingt dann mit der Schwebungsfrequenz periodisch zwischen dem
Oszillator 1 und dem Oszillator2.
70
KAPITEL 2. SCHWINGUNGEN
Kapitel 3
Wellen
3.1 Von Schwingungen zu Wellen
Jeder Oszillator ist an seinen Nachbarn gekoppelt. Dadurch wird ein rumlicher Transport von Schwingungsenergie erzielt. Jeder Oszillator %hinkt seinem
vorherigen Nachbarn in der Phase hinterher.
y(t! x) = y0 sin(!t ; kx)
Wir sehen, da diese Gleichung von Zeit und Ort abhngt.
Schwingung: y = y(t)
Welle: y = y(t! x)
Eine Welle beschreibt den rumlichen Transport von Schwingungsenergie ohne
Transport von Materie.
Um den Betrag der Wellenlnge zu erhalten, mu man einige berlegungen bezglich der Phase der einzelnen Wellenpunkte anstellen. Fr benachbarte Orte
mit gleicher Phase (also nicht die unmittelbaren Nachbarn) gilt kx = 2 , also
x = 2k . Der Abstand dieser benachbarten Orte betrgt also gerade = 2k und
wird Wellenlnge genannt. k = 2 heit Wellenzahl.
71
KAPITEL 3. WELLEN
72
Die Geschwindigkeit, mit der sich ein Ort bestimmter Phase bewegt (zum Beispiel
der Ort mit dem Amplitudenmaximum), heit Phasengeschwindigkeit c . In der
Zeit T = 2! hat sich der %bestimmte Ort 2um die Wellenlnge bewegt. Daraus
erhalten wir die Geschwindigkeit c = T = 2!k = !k
3.2 Die Wellengleichung
Die Gleichung
u(x! t) = u0 sin(!t ; kx)
beschreibt eine Welle. u(x! t) ist die L
sung der folgenden Dierentialgleichung:
d2u ; 1 d2u = 0
dx2 c2 dt2
!
In vektorieller Schreibweise lauten die Formeln dann (mit ;
k parallel zur Ausbreitungsrichtung der Welle):
u(~r! t) = u0 sin(!t ; ~k ~r)
d2u + d2u + d2u ; 1 d2u = 0
dx2 dy2 dz 2 c2 dt2
3.3 Wellenarten
3.3.1 Longitudinale Wellen
Bei diesen Wellen verluft die Bewegungsrichtung des Oszillators parallel zur Ausbreitungsgeschwindigkeit der Welle.
3.3.2 Transversale Wellen
Die Bewegungsrichtung des Oszillators steht hierbei senkrecht zurAusbreitungsgeschwindigkeit der Welle.
3.3.3 Ebene- und Kugelwellen
Als Wellenfront wird die Menge aller Punkte gleicher Phase bezeichnet. Bei
ebenen Wellen bilden diese Punkte eine Ebene, wobei die Wellenfront bei Kugelwellen eine Kugel oder Halbkugel darstellt. Im zweidimensionalen spricht man jedoch
von Kreiswellen. Als klassisches Beispiel werden hier die Wellen auf der Oberche
von einem Wassergef, in das ein Stein el, genannt.
3.3.4 Beugung und Huygenssches Prinzip
Auf die Frage %Wie gelangt eine Schallwelle um die Ecke? gibt uns das Huggensche
Prinzip Antwort:
3.3. WELLENARTEN
73
Jeder Punkt einer Wellenfront kann als Ausgangspunkt einer Kugelwelle betrachtet
werden als sogennante Huygenssche Elementarwelle.
Die Summe ber diese Kugelwellen ergibt die neue Wellenfront. Eine Welle, die nun
auf ein Hindernis trit, wird daran %gebeugt , das heit, aufgrund des Huygensschen
Prinzips kommt es zu einer Abweichung von der ursprnglichen Ausbreitungsrichtung.
3.3.5 Stehende Wellen
Diese Wellen %leben nur in einem genau abgegrenzten Bereich. An den Enden
(gegeben durch die Ausbreitungsrichtung) von diesem Bereich treten Reexionen
auf. Dadurch entsteht eine berlagerung von der einlaufenden und der reektierten Welle. Bei bestimmten Frequenzen (bestimmt in Bezug auf die Gr
e des %Lebensbereiches ) bilden sich stationre Schwingungsmuster aus, die stehende Wellen
genannt werden.
Reexionen k
nnen an zwei verschiedenartigen Enden auftreten:
a) geschlossenes Ende, Schwingungsknoten
Bei Saitenmusikinstrumenten ist dies der Fall das Saitenende ist eingespannt.
Eine stehende Welle entsteht, falls l = n 2 mit n 2 N gilt. Durch c = f erhalten
wir die Resonanzfrequenz f = nc
2l . l ist hierbei die Lnge des %Lebensbereiches , bei
einem Musikinstrument die Lnge der Saite.
Fr l = 2 erhalten wir die Grundschwingung der Saite l = 2 2 die erste Oberschwingung,. . .
b) oenes Ende, Schwingungsbauch
Hier erhalten wir die Grundschwingung schon bei l = 4 . Folglich gilt fr die
Resonanz- oder Eigenfrequenz f = nc
4l .
Bei Reexionen am geschlossenen Ende tritt ein Phasensprung mit dem Betrag
auf.
KAPITEL 3. WELLEN
74
3.4 Beispiel einer mechanischen Welle
Wir betrachten eine Schallwelle in einem Stab genauer. Durch das Anschlagen mit
einem Hammer erreichen wir eine elastische Deformation. Dadurch breitet sich eine
Lngswelle aus. Die Bedeutung der Variablen:
A Stabquerschnitt
dx Lngenelementchen
(x) Druck (Zugspannung)
Dichte
E Elastizittsmodul
u(x) Auslenkung aus der Ruhelage
Na, dann rechnen wir ein bissele:
F (x) = (x)A
F (x + dx) = (x)A + x dxA
d
du
wobei: = "E = E du
dx =) dx = E dx2
d2u dx
dF = EA dx
2
dm = N = Adx
2
dF = dma = dm ddtu2
du dx = Adx d2u
EA dx
2
dt2
Durch Vergleich mit der Wellengleichung erhalten wir die Schallgeschwindigkeit im
Stab
s
c = E
3.5. ENERGIETRANSPORT DURCH DIE WELLE
75
3.5 Energietransport durch die Welle
Wir betrachten ein Massenelement mit der Masse dm und dem Volumen dV .
Dichte
u0 Amplitude
! = 2f
Fr die kinetische Energie gilt:
2 2 2
dEkin = dm
2 u0! cos (!t ; kx)
Fr die cos2 Funktion erhalten wir den Zeitmittelwert cos2 (!t ; kx) = 21 .
2 2 dV 2 2
dEkin = dm
4 u0! = 4 u0! = dEpot
Die Gesamtenergie betrgt
dE = dEkin + dEpot = 2 u20 !2 dV
Gesamtenergiedichte (Energie pro Volumen):
u2!2
W = dE
=
dV 2 0
Der Energietransport in der Zeit t durch die Querschnittsche A senkrecht der
Ausbreitungsrichtung der Welle betrgt demnach:
E = WV = WAx = WAct
Die Intensitt ist der Energietransport pro Zeit und Durchschnittsche, die Energiestromdichte.
t) = Wc = u2!2 c
I = E(A!
At
2 0
3.6 Der Dopplereekt
Bewegt sich eine Schwingungsquelle relativ zu einem Empfnger verurscht dies eine
Frequenznderung. Wenn ein Auto an einem Fugnger hupend vorbeifhrt, h
rt
dieser die Hupe in drei unterschiedlichen Tonh
hen. Die gesendete Frequenz wir
mit f0 , die empfangene Frequenz mit f 0 bezeichnet.
a) bewegte Quelle
Mit der Geschwindigkeit v > 0 fr die Annherung ndert sich durch die Bewegung des Senders.
0 = 0 ; vT0
Dabei ist vT0 die Strecke, um die sich die Quelle in der Periode T bewegt hat.
0 = cT1 ; vT0 = (c ; v)T0 = c f; v
0
Damit erhalten wir fr die empfangene Frequenz:
f 0 = c0 = ccf;0v = 1 f;0 v
c
KAPITEL 3. WELLEN
76
b) bewegter Beobachter
Auch hier gilt die Geschwindigkeit v > 0 fr die Annherung.
f 0 = T1 = c + v = fc0 (c + v) = f0 (1 + vc )
0
3.7 Kohrenz und Interferenz
Die Amplituden harmonischer Wellen addieren sich zur Gesamtamplitude sogenanntes Superpositionsprinzip. Besteht zwischen zwei Wellen an jedem Ort in einem bestimmten Raumbereich eine feste, das heit eine zeitunabhngige, Phasenbeziehung, so heien die beiden Wellen kohrent. Vorraussetzung ist, da beide
Wellen die gleiche Frequenz haben. berlagert man kohrente Wellen, kommt es
zur Interferenz. Orte mit Phasenverschiebungkommen in zwei Fllen vor:
a) Wellen gleichphasig
Die Amplituden beider Wellen addieren sich. Es entsteht konstruktive Interferenz
mit maximaler Intensitt.
b) Wellen gegenphasig
Die Amplituden subtrahieren sich. Es bilden sich Orte mit minimaler Intensitt,
bis zur Ausl
schung das ist die destruktive Interferenz.
3.8 Dispersion
Wir betrachten ein Wellenpaket, das sich mit konstanter Geschwindigkeit in eine
Richtung ausbreitet. Es besteht aus einer Mischung von Sinuswellen unterschiedlicher Frequenzen. Ist die Phasengeschwindigkeit c frequenzabhngig, so %entwirren
sich die verschiedenen Frequenzen im Laufe der Zeit das ist Dispersion. Das Wellenpaket verbreitert sich dadurch. Die Geschwindigkeit, mit der sich das Maximum
des Wellenpaketes ausbreitet, hei Gruppengeschwindigkeit.
Kapitel 4
Thermodynamik
4.1 Wrmeenergie und Temperatur
4.1.1 Temperatur und der Nullte Hauptsatz
Wir haben bisher potentielle Energie und kinetische Energie (mechanische Energien)
kennengelernt. Neu ist die Wrmeenergie. Durch Reibung werden mechanische
Energieformen in Wrmeenergie umgewandelt
) Erh
hung der Temperatur T.
Zwei K
rper in thermischem Kontakt tauschen so lange Wrmeenergie aus, bis ihre
Temperaturen gleich sind.
)Nullter Hauptsatz: Zwei K
rper im thermischen Gleichgewicht haben die
selbe Temperatur.
4.1.2 Temperaturskala / absoluter Nullpunkt
die Celsius - Skala:
0 C: Schmelzpunkt von Wasser
100C: Siedepunkt von Wasser (bei 1 atm)
Nachteil: Nullpunkt willkrlich gewhlt
das Verhalten idealer Gase
Alle ideale Gase zeigen bei V= const linearen Anstieg des Druckes mit der Temperatur.
77
KAPITEL 4. THERMODYNAMIK
78
P(T)
Gas wird flüssig
=> nicht mehr ideal
-273,15
T [°C]
Extrapolation fr p ! 0 liefert fr alle idealen Gase: -273,15C.
Denition der absoluten Temperatur T (Kelvin - Skala):
'T] = 1 K (1 Kelvin)
Nullpunkt: 0 K = -273,15 C
Temperaturdierenz: 1K entspricht 1C
Das Gasthermometer
Ideales Gas bei V = const.
h
p = % h g
4.1.3 Wrmeausdehnung
Lngenausdehnung
Als Funktion der Temperatur ndern Festk
rper ihre Lnge:
l = T
l
4.1. WRMEENERGIE UND TEMPERATUR
79
l: Lnge
l: Lngennderung
T: Temperaturnderung
: Wrmeausdehnungskoe&zient
'] = K1 ist meistens > 0 bei Gummi und einigen Kunststoen aber < 0
Volumenausdehnung
bei Festk
rpern, Flssigkeiten und Gasen:
V = T
V
: Volumenausdehnungskoe&zient '] = K1
ist meistens > 0 und bei
Flssigkeiten typischerweise ca. 50 gr
er als bei Festk
rpern.
Fr Festk
rper gilt: = 3 4.1.4 Technische Verfahren zur Temperaturmessung
Flssigkeitsthermometer :
nutzen die thermische Ausdehnung einer Flssigkeit (Wasser, Alkohol, ...).
Bimetallthermometer:
Zwei miteinander fest verbundene Metallstreifen mit unterschiedlichem verbiegen sich bei Temperaturnderung.
Widerstandsthermometer:
nderung des elektrischen Widerstandes mit der Temperatur. Beispiel: Platin
- Film als Pt - 100 - Widerstand
Thermoelemente
Strahlungspyrometer:
berhrungslose Messung hoher Temperaturen durch Messung der emitierten
Wrmestrahlung
(Rot- / Weiglut) ! Oberchentemperatur der Sonne = 5700 C.
4.1.5 Wrmeenergie und spezische Wrme
Ben
tigte Wrmeenergie Q, um K
rper der Masse m um T zu erwrmen:
Q = c m T
wobei c die spezische Wrme meint: 'c]= 1 kgJK
C= c m: Wrmekapazitt 'C]= 1 KJ
4.1.6 Phasenumwandlungen und latente Wrme
Umwandlung fest $ ssig
Um einen Festk
rper zu verdampfen, ist Zufuhr von thermischer Energie erforderlich
(sog. Schmelzwrme):
QSchmelz = m cSchmelz (!spezische Schmelzwrme ' kgJ ])
KAPITEL 4. THERMODYNAMIK
80
Umwandlung ssig $gasfrmig Um eine Flssigkeit zu verdampfen, ist
Zufuhr von thermischer Energie erforderlich (sog Verdampfungswrme):
QV erd = m cV erd (!spezische Verdampfungswrme ' kgJ ])
Bei erneuter Kondensation wird QV erd wieder frei (Kondensationswrme).
T
[°C]
H 2O
Dampf
Wasser&
Dampf
100
Wasser
Eis &
Wasser
0
Q
Schmelzwärme
Verdampfungswärme
Eis
sog. "latente Wärmen"
4.1.7 Phasendiagramme
Temperatur der Phasenbergnge ist druckabhngig.
Bsp H2 O:
Bsp.: Wasser
Phasendiagramm
P
Fluessig
Fest
Tripelpunkt
Gasfoermig
T
unter Druck wird Eis ssig.
Wandern von Gletschern
Schlittschuhlaufen
Draht wandert durch das Eis:
4.1. WRMEENERGIE UND TEMPERATUR
81
Temperatur der Phasenbergnge ist abhngig von gelsten Stoen.
Bsp.: Gefrierpunktsreduzierung von H2 O durch Kochsalz bis -21C je nach NaCl Konzentration.
ohne Keime Verzug der Phasenbergnge
unterkhlte Flssigkeiten (reines Wasser bis -10 C)
berhitzte Flssigkeiten (Zur Vermeidung: Siedesteine als Keime)
Die Dichte - Anomalie des Wassers
Wasser dehnt sich beim Gefrieren aus.
maximale Dichte bei 4 C
V(T)
Hg
H 2O
4
T
[°C]
4.1.8 Ideale und reale Gase
Die Stomenge und das Gesetz von Avogadro
Gase enthalten sehr viele Molekle. Statt die Molekle einzeln zu zhlen, whlt
man eine gr
ere Einheit: das sog. mol
.
Ein mol ist die Menge eines Stoes, die 6,022045 1023 Teilchen enthlt.
Basisgr
e 'n]= 1 mol
Avogadro - Konstante: NA = 6,022045 1023 (Teilchen/ mol)
groes N: Anzahl der Teilchen
12 g des Kohlensto&sotops 126 C enthalten 6,022045 1023 Atome.
Massenzahl= Zahl der Protonen und Neutronen zusammen.
Kernladungszahl= Zahl der Protonen im Kern
Die Molmasse mmol ist die Masse von 6,022045 1023 Teilchen (1 mol) eines Stoffes. Die Molmasse betrgt genausoviel Gramm wie die Massenzahl bzw. die rel.
KAPITEL 4. THERMODYNAMIK
82
Moleklmasse angibt. Das Molvolumen (Vmol ) eines idealen Gases betrgt unter
Normalbedingungen (1 atm, 273,15 K):
Vmol = 22,414 10;3m3 = 22,414 l
(Gesetz von Avogadro)
4.1.9 Die Zustandsgleichung fr ideale Gase
Experimentell ndet man bei idealen Gasen:
fr T= const gilt: pV = const
)
p V1
p V T
) pTV
Gesetz von Boyle - Mariotte
= const. Gesetz von Gay - Lussac
V n Volumen Stomenge
ideale Gasgleichung: p V = n R T
Berechnung von R nach dem Gesetz von Avogadro:
p= 1 atm = 1,013 105 mN2 T = 273,15 K n= 1mol Vmol = 22! 4 10;3
) universelle Gaskonstante: R = 8,314 molJK
(R ist fr alle idealen Gase
gleich)
Teilchenzahl N: N = n NA
1023
N
= n 6022
mol )n= NA
Fr die ideale Gasgleichung ergibt sich: p V = n R T = N NRA T = N k T
Boltzmann - Konstante: k = NRA = 1,3807 10;23
)
4.2 Mikroskopische Denition des idealen Gases
Drei Bedingungen:
1. Das Gas besteht aus einer groen Zahl von Teilchen, die untereinander und
mit den Wnden nur elastische St
e ausfhren.
2. Groer Teilchenabstand, d.h. Gefvolumen Eigenvolumen der darin enthaltenen Teilchen.
3. Zwischen den St
en bewegen sich die Teilchen wechselwirkungsfrei.
4.2. MIKROSKOPISCHE DEFINITION DES IDEALEN GASES
83
4.2.1 kinetische Gastheorie
Die Grundidee
Stahlkugeln prasseln in dichter Folge auf die Stahlwand und werden an ihr reektiert.
Mikroskopische Deutung des Gasdruckes und der Temperatur:
Molekle des idealen Gases prasseln auf Gefwnde
+
werden elastisch reektiert
+
bertragen Impuls p = 2mv
+
F =p_ , Kraft auf Wand
Flaeche A
x
N:
V
Anzahldichte, Zahl der Teilchen im Volumen
elastischer Sto mit der rechten Wand (s.o.) mit vx als der Geschwindigkeit in x Richtung:
vx > 0: 2NV Anzahldichte derjenigen Moleke, die auf die Wand zuiegen
Annahme: jvxj fr alle Molekle gleich
Zahl der Molekle, die in t auf die Wand treen:
N(t)= 2NV A |{z}
x Impulsbertrag in t:
vx t
p = N(t)2mvx= 2NV A vx t2mvx2
= NV Amvx2 t
Kraft: F = p=
_ pt = NV Amvx2
Druck: p = AF = NV mvx2
KAPITEL 4. THERMODYNAMIK
84
Nmvx2
vgl.: p V= N R T
(ideale Gasgleichung)
) 21 R T = 12 mvx2
In Wirklichkeit ist 23 kT die mittlere kinetische Energie eines Teilchens bei seiner
statistischen Wrmebewegung.!mikroskopische Deutung der Temperatur.
)pV=
Gleichverteilungssatz (quipartitionstheorem):
Die thermische Energie eines Molekls verteilt sich gleichmig auf alle seine Freiheitsgrade. Jeder Freiheitsgrad hat die mittlere kinetische Energie:
E kini= 12 k T
Oft haben wir es jedoch mit mehr als drei Freiheitsgraden zu tun (z.B. Schwingung
und Rotation von Moleklen).
Atom im Festk
rper: 6 Freiheitsgrade
4.2.2 Maxwellsche Geschwindigkeitsverteilung
Teilchenzahl: N
Temperatur: T
Moleklmasse: m
Betrag der Moleklgeschwindigkeit: v
Sie f(v) dv = Zahl der Molekle mit Geschwindigkeitsbetrag zwischen v und (v+dv)
Man kann zeigen:
m v2
f(v) = const N
4v
|e;{z2 kT}
|{z}2 statisches Gewicht Boltzmann; Faktor e; Energie
kT
f(v)
T1
T2 > T1
VW(T1)
VW(T2)
Flche unter Geschwindigkeitsverteilungsfunktion immer = N!
wahrscheinlichste
Geschwindigkeit:
q
vw =
2kT
m
mittlere Geschwindigkeit:
q
v = p2 vw =
8kT
m
vgl.: quadratisch
gemittelte Geschwindigkeit:
q
vrms =
3kT
m
4.3. PARTIALDRUCK, DAMPFDRUCK, LUFTFEUCHTIGKEIT
85
4.3 Partialdruck, Dampfdruck, Luftfeuchtigkeit
4.3.1 Daltonsches Gesetz der Partialdrcke
Betrachte Gasgemische:
Der Druck, den ein Gasanteil ohne Anwesenheit der brigen gase ausben wrde,
heit Partialdruck dieses Gases.
Beim idealen Gas ist der Gesamtdruck eines Gases gleich der Summe der Partialdrcke seiner komponenten (Daltonsches Partialdruckgesetz).
4.3.2 Dampfdruck
Im Gleichgewicht verlassen pro Zeiteinheit genausoviele Molekle die Flssigkeit,
wie Molekle in sie eintreten.
flüssig
Der Partialdruck der ssigen Komponente, der im Gleichgewicht ber der Flssigkeit herrscht, heit der Dampfdruck der Flssigkeit bei dieser Temperatur.
Die
p
Zahl der Molekle, die die Flssigkeit pro Zeiteinheit verlassen, wchst mit fv2 g
und damit mit T.
) Dampfdruck steigt mit wachsendem T
4.3.3 Siedepunkt
Erreicht der Dampfdruck der Flssigkeit den ueren Gesamtdruck, so ist es m
glich, da sich in der Flssigkeit Gasblasen bilden.
!im sog. Siedepunkt gilt:
Dampfdruck = Gesamtdruck
)Je kleiner der Gesamtdruck, desto niedriger ist der Siedepunkt.
4.3.4 Relative Luftfeuchtigkeit im Taupunkt
Partialdruck H2 O 100%
relativeLuftfeuchtigkeit = Dampfdruck
(T ) H2 O
Taupunkt: Temperatur, bei der (bei gegebenem H2O - Partialdruck) die relative
Luftfeucktigkeit 100 % erreicht.
KAPITEL 4. THERMODYNAMIK
86
4.4 Reale Gase: van der Waalsche Zustandsgleichung
ideale Gase: p V = n R T
ideale
Gasgleichung
van der
reale Gase: (p + aVn22 ) (V - b n) = n RT
Waalsche Zustandsgleichung
2
Binnendruck aVn2 : Zustzlich zum ueren Druck p der Gefwnde auf das Gas
wirken auf das Gas noch innere anziehende Krfte.
van der Waalsches Kovolumen b n: das fr die Gasmolekle verfgbare Volumen
wird durch das Eigenvolumen vermindert.
Beachte: beim realen Gas wird p erh
ht, V dezimiert!
P
reales Gas
C (kritischer Punkt)
T5
T4
T3 = TC
T2
T1
V
4.5 Joule - Thomson - Eekt und Gasverssigung
nach Linde
Joule - Thomson - Eekt:
Unterhalb einer sogenannten Inversionstemperatur khlen Gase beim Expandieren ab, weil sie Arbeit gegen die zwischenmolekularen Anziehungskrfte verrichten mssen.
Die erforderliche Energie wird der Wrmebewegung der Gasmolekle entzogen.
;! Linde - Verfahren zur Luftverssigung:
4.6. ZUSTANDSNDERUNGEN UND KREISPROZESSE IDEALER GASE 87
4.6 Zustandsnderungen und Kreisprozesse idealer
Gase
4.6.1 Der erste Hauptsatz der Thermodynamik
innere Energie: die in einem System gespeicherte Energie (v.a. thermische Ener-
gie)
Die Summe der einem System von auen zugefhrten Wrmeenergei Q und der
zugefhrten (z.B. mechanischen) Arbeit W ist gleich der Zunahme U seiner
inneren Energie:
U = Q + W
Erster Hauptsatz der Thermodynamik (entsprechend dem Energieerhaltungssatz):
Es ist unm
glich, Energie aus dem nichts zu gewinnen.!
ander Formulierung:
Ein perpetuum mobile erster Art ist unm
glich.!
Dieser erste Hauptsatz der Themodynamik ist ein Erfahrungssatz und noch nicht
bewiesen.
speziell fr das ideale Gas:
Es gibt zwei M
glichkeiten der Energiezufuhr / -abfuhr:
mechanische Kompression / Expansion:
dW =F dx = p A dx = -p dW
Wichtig: Vorzeichenkonvention:
dW > 0: dem System wird Energie zugefhrt, d.h. an dem System wird
Arbeit verrichtet (d.h.Kompression ,dV < 0).
dW < 0: System verrichtete Arbeit an seiner Umgebung, d.h. die Energie des
Systems nimmt ab (d.h. Expansion ,dV > 0).
Zufuhr (dQ > 0) bzw. Abfuhr (dQ < 0) von Wrmeenergie dQ
)
dU = dQ + dW = dQ - p dV
(1. Hauptsatz beim idealen Gas)
4.6.2 Die spezischen Molwrmen Cp und Cv idealer Gase
Bezieht man die spezischen Wrmen nicht auf 1 kg (Masse) sondern auf ein Mol
(Stomenge), so spricht man von den spezifischen Molwrmen Cmolar :
Q = n Cv T
J K
mit n als Stomenge und 'Cmolar ] = 1 mol
Bei Gasen mu man dabei zwei Flle unterscheiden: konstanter Druck oder konstantes Volumen.
innere Energie U eines idealen Gases aus N einatomigen Teilchen
U = N fEking = N 23 k T
KAPITEL 4. THERMODYNAMIK
88
= n NA 32 k T
= n 32 R T
) U = n 32 R T T
oder allgemein fr Teilchen mit f Freiheitsgraden:
U = n f2 R T T
Fr die Freiheitsgrade gilt:
einatomiges Gas ) f = 3
zweiatomiges Gas ) f = 5
Spezische Molwrme bei konstanten Volumen
1. HS: U = Q - p V, wobei V = 0, da V = const
)U = n f2 R T T
Q = n Cv T
ergibt: Cv = f2 R
(man erinnere sich: R ist die universelle Gaskonstante)
Spezische Molwrme bei konstantem Druck
Das Gas wird mit Q erwrmt und dehnt sich daher aus. Das Gas verrichtet so
Arbeit anch auen (W < 0) und gibt dadurch einen Teil des zugefhrten Q
in Form von mechanischer Arbeit wieder nach auen ab. Fazit: Es ist hier mehr
Wrme Q erforderlich, um eine bestimmte Temperatur T zu erreichen, als wenn
das Volumen konstant bliebe.
Cp=Cv + R
K = CCpv = f +2
!sog. Adiabatenkoeffizient
f
4.6.3 Zustandsnderungen idealer Gase
Vorbemerkung
Unser System sei (in diesem Abschnitt) eine abgeschlossene Stomenge eines
idealen Gases (n = 1 mol)
Der Zustand! bezeichnet die Gesamtheit der makroskopischen Eigenschaften
des Systems
Alle Zustandsgr
en werden durch den Zustand eindeutig festgelegt
Isochore Prozesse (V = const)
V = 0 ) W = 0
)Q = U = Cv T
= f2 R T
4.6. ZUSTANDSNDERUNGEN UND KREISPROZESSE IDEALER GASE 89
P
Zustand 1
Zustand 2
V
Erwrmen oder Abkhlen des Systems ohne Verrichtung mechanischer Arbeit.
Isobare Prozesse (p = const)
Q = U + p V
= f2 R T + R
| {zT}
| {z }
U
;W
Erwrmen oder Abkhlen unter Verrichtung mechanischer Arbeit aufgrund der
Volumennderung.
P
Zustand 1
Zustand 2
V
Isotherme Prozesse (T = const)
T = const
m
U = 0, d.h. keine nderung der inneren Energie
m (1. Hauptsatz)
Q = - W
P
Zustand 1
T= const
<=> p V = const
Zustand 2
V
KAPITEL 4. THERMODYNAMIK
90
W = RTln vv12 = ;Q
Adiabatische Prozesse (Q = 0)
Kompression oder Expansion ohne Wrmeaustausch mit der Umgebung
)Q
=0
W = U
C
v
T V R = const
T V ;1 = const
Adiabaten - Gleichungen
pV = const
Poisson - Gleichungen oder
P
Zustand 2
Adiabate
Zustand 1
V
Polytrope Zustandsnderungen
isotherm: ideale Ankopplung an Wrmebad mit T = const )p V = const
adiabatisch: keinerlei Wrmeaustausch mit Wrmebad )p V K = const
Adiabaten verlaufen im p - V - Diagramm steiler als Isothermen (da K = CCpv >
1)
polytrop: Zwischenfall (Realfall): unvollstndiger Wrmeaustausch )p V = const
mit 1 < < K
P
isotherm
polytrop
adiabatisch
V
4.6. ZUSTANDSNDERUNGEN UND KREISPROZESSE IDEALER GASE 91
4.6.4 Der Carnotsche Kreisproze
Kreisproze
Eine Abfolge thermodynamischer Prozesse, an deren Ende eine System wieder den Ausgangszustand (gleiche p, V, T wie am Anfang) erreicht, heit
Kreisproze.
Kann ein Kreisproze in beide Richtungen verlaufen, so heit er reversibel.
Ablauf des Carnot - Prozesses
P
1
Isotherme
T1
2
Adiabate
4
T2
3
V
Der Carnot - Proze ist ein Kreisproze aus zwei Isothermen und zwei Adiabaten.
Man braucht dazu drei Dinge:
Das thermodynamische System, das den Proze durchluft (abgeschlossene
Menge idealen Gases), sog. arbeitsgas.
(riesiges) Wrmereservoir der Temperatur T1.
(riesiges) Wrmereservoir der Temperatur T2.
Carnot - Maschine
Waermereservoir
Waermereservoir
mit
mit
T1
Arbeitsgas
T2< T1
Wrmereservoirs sind riesige Wrmespeicher mit (fast) unendlicher Kapazi-
tt und gleichbleibender Temperatur.
KAPITEL 4. THERMODYNAMIK
92
beim Carnot - Proze passiert folgendes:
1 ! 2: isotherme Expansion bei idealer Ankopplung an das Wrmereservoir T1
3 ! 4: isotherme Kompression bei idealer Ankopplung an das Wrmereservoir T2
2 ! 3 und 4 ! 1: adiabatische Expansion bzw. Kompression, d.h. Q = 0 d.h.
Abkopplung von beiden Wrmebdern, kein Wrmeaustausch.
Die vier Teilschritte des Carnot - Prozesses:
1 ! 2: isotherme Expansion bei T1:
T = const ) U = 0
Q1 = -W12=
Das bei T1zugefhrte Q1 wird vollstndig wieder in Form von mechanischer Arbeit
abgegeben.
2 ! 3: adiabatische Expansion von V2 auf V3
Die beim Expandieren nach auen abgegebene oder verrichtete Arbeit entstammt
der inneren Energie des Systems ) abkhlung auf T2
3 ! 4: isotherme Kompression bei T2
Die bei der mechanischen Kompression am System verrichtete mechanische Arbeit
iet vollstndig in das kalte Reservoir ab.
4 ! 1: adiabatische Kompression von V4 auf V1
Q = 0
W41 = U = U (T1) - U(T2 ) > 0
Beachte: W41 + W23 = 0
Adiabatische Kompression erwrmt das Arbeitsgas von T2 auf T1 .
fr die beiden Adiabaten gilt ferner:
2 !3 T1V2K ;1 = T3 V3K ;1
(?)
K
;
1
K
;
1
(? ?)
4 !1 T1V1 = T2 V4
V
V
2
3
(?) : (? ?)
(beim Carnot - Proze) (???)
V1 = V4
4.6. ZUSTANDSNDERUNGEN UND KREISPROZESSE IDEALER GASE 93
4.6.5 Energiebilanz und Wirkungsgrad der Carnot - Maschine
Energiebilanz
(warm)
T1
Q1
=
Wges
+
Q2
Q1
Carnot Wges
Maschine
Q2
T2
(kalt)
Q1 = R T1 ln VV21
(???)
Q1 = R T2 ln VV43 = R T2 ln VV12 ) QQ12 = - TT21
Wges = W12 + W23 + W34 + W41
= - R T1 ln VV21 - R T2 ln VV34
= - R T1 ln VV21 + R T2 ln VV34
Wges = - R (T1 - T2 ) ln VV12 < 0
das heit, es wird vom System Arbeit nach auen abgegeben: pro Umlauf Wges
Wirkungsgrad
Ziel einer Wrmekraftmaschine ist die Umwandlung von Wrmeenergie in mechanische Arbeit. Dies gelingt allerdings auch bei der noch so idealen, reibungsfrei
laufenden Carnot - Maschine nie zu 100%.
Wirkungsgrad einer Carnot - Wrmekraftmaschine:
jWges j
pro Zyklus vom System verrichteteArbeit
= pro Zyklus
dem warmen Reservoir entnommeneWaerme = j Q1 j
fr Carnot - Proze:
V2
max = R(TR1T;1Tln2 )Vln2 V1 = T1 T;1 T2 = 1 - TT21 < 1
V1
nicht - ideale Maschine (Reibung) ) < max
KAPITEL 4. THERMODYNAMIK
94
4.6.6 Die rckwrts laufende Carnot - Maschine
Energiebilanz
Kompression bei hoher Temperatur Expansion bei tiefer Temperatur
P
1
T1
2
4
T2
3
V
Alle Energien wechseln das Vorzeichen:
(warm)
T1
Q1
=
Wges
+
Q2
Q1
Carnot Wges
Maschine
Q2
T2
(kalt)
Unter Verrichtung von mechanischer Arbeit wird Wrmeenergie Q2 dem klteren Reservoir entzogen und in das wrmere Reservoir gepumpt.
Verwendung als Kltemaschine (Khlschrank): Nutzen: unterem Reservoir wird
Q2 entzogen.
Wirkungsgrad als Kltemaschine:
R T2 ln VV21
T2
2j
k = jj WQges
=
j R(T1 ;T2) ln VV12 = T1;T2
k = T1T;2T2
k ist gro, wenn (T1 - T2 ) klein ist.
Verwendung als Wrmepumpe:
Nutzen: Energiezufuhr an das wrmere Reservoir
4.6. ZUSTANDSNDERUNGEN UND KREISPROZESSE IDEALER GASE 95
Wirkungsgrad als Wrmepumpe:
R T1 ln VV21
1j
T1
=
w = jj WQges
j R(T1 ;T2) ln VV21 = T1 ;T2
w = T1T;1T2 = 1;1T2 > 1 (!)
T1
4.6.7 Stirling - Proze und Heiluftmotor
Stirling - Proze: Kreisproze aus zwei Isochoren und zwei Isothermen.
Im Gegensatz zum Carnot - Proze treten noch Q3 und Q4 auf mit:
Q2 = -Q4 = cv (T2 - T1 )
Stirling Carnot
Falls Q2 nicht zwischengespeichert und als Q4 wieder zugefhrt wird, hat die
Stirling - Maschine einen geringeren Wirkungsgrad als die Carnot - Maschine.
Technische Realisierung mit (teilweiser) Zwischenspeicherung von Q2: Heiluft-
motor
(!ist kein Verbrennungsmotor).
4.6.8 Technische Khlschrnke und Wrmepumpe
Kompressor
Q2
Q1
Kühlung durch
Aufnahme
latenter Wärme
beim Verdampfen
Kompression
Abgabe der
Kondensationswaerme
Drosselventil
Verssigung durch Kompression
Verdampfung nach Entspannung beim Drosselventil
KAPITEL 4. THERMODYNAMIK
96
4.6.9 Transport von Wrmeenergie
Man unterscheidet drei Prozesse:
a) Wrmeleitung:
Medium erforderlich
kein Transport von Materie
dQ
dt
= - A dT
dx
wobei:
dQ : Wrmestrom
dt
: Wrmeleitfhigkeit des Materials
A: Querschnittsche
dT : Wrmeunterschied pro Lnge
dx
b) Konvektion:
Medium erforderlich
Transport von Materie wegen = (T)
Beispiel: warme Luft steigt nach oben.
c) Wrmestrahlung:
kein Medium erforderlich
K
rper emittiert umso mehr elektromagnetische Wrmestrahlung, je gr
er
T ist.
Beispiel: Glhen ist Wrmestrahlung im sichtbaren Bereich.
4.7 Entropie und der zweite Hauptsatz
4.7.1 Formulierung des zweiten Hauptsatzes
Es gibt Prozesse, die nach dem ersten Hauptsatz zwar erlaubt wren, die aber
trotzdem nicht beobachtet werden.
(1) Wrmeenergie iet von selbst immer nur vom wrmeren zum klteren K
rper,
nie jedoch umgekehrt.
Der zweite Hauptsatz der Thermodynamik ist ein Erfahrungssatz und nicht
beweisbar (bungsaufgabe).
quivalente Formulierung:
(2a) Es gibt keine periodisch arbeitende Maschine, die nichts anderes tut, als einem
Reservoir Wrmeenergie zu entziehen und diese in mechanische Arbeit umzuwandeln.
oder krzer:
(2b) Ein perpetuum mobile zweiter Art ist unm
glich.
Wieso sind (2a) und (2b) zu (1) quivalent?
4.7. ENTROPIE UND DER ZWEITE HAUPTSATZ
97
Gbe es eine solche Maschine, so k
nnte sie eine Wrmepumpe antreiben, die Energie Q vom Klteren zum Wrmeren pumpt, was (1) wiederspricht.
Es gilt sogar:
Es gibt keine Wrmekraftmaschine, die einen h
heren Wirkungsgrad hat, als die
ideale Carnot - Maschine.
Beweis:
zwei ideale Carnot - Maschinen, eine als Wrmekraftmaschine, die andere als Wrmepumpe werden zusammengeschaltet.
1 heben sich die Ttigkeiten beider Maschinen gerade auf. ErWegen WkM = WP
setzte man nun jede Carnot - Maschine durch eine mit h
herem Wirkungsgrad,
dann wrde mehr Wrme ins obere Reservoir gepumpt als diesem entzogen wrde
) Widerspruch zur Formulierung (1).
4.7.2 Reversible und irreversible Prozesse
Beispiel fr einen reversiblen Proze: die Carnot-Maschine.
Wieso ist dieser Proze reversibel?
Ich kann jederzeit W wieder verwenden, um Q1 und Q2 mit einer Carnotschen
Wrmepumpe ohne Energiebedarf von auen zurckzupumpen!.
Beispiel fr einen irreversiblen Proze ist jede unumkehrbare Abkhlung.
4.7.3 Reduzierte Wrme und Entropie
Gesucht ist ein quantitatives ma fr die Reversibilitt eines Kreisprozesses.
L
sung: reduzierte Wrmemenge dQ
T mit
dQ: ausgetauschte Wrmemenge
T: Temperatur, bei der der Austausch stattfand
deniere dS:= dQ
T bei reversiblen Prozessen
Die Entropie S wird deniert als eine Gr
e, deren nderung dQ
T betrgt.
Folge: falls Qrev: = 0, so ist S = 0
) keine Entropienderung S bei adiabatischen Prozessen.
Adiabaten sind somit Linien konstanter Entropie, sog. Isentropen.
Reduzierte Wrme und Entropie beim Carnot - Proze
Wir fanden:
Q1 = - T1
Q2
T2
, TQ1 1
+ TQ2 2 = 0
, Sc = 0
Die Summe aller Entropienderungen bei einem Zyklus des Carnot - Prozesses ist
Null dies gilt fr beide Verlaufrichtungen.
! Die Entropie S hngt nur vom Zustand ab, nicht aber vom Weg, auf dem dieser
Zustand erreicht wurde Die Entropie ist eine sog. Zustandsgre.
KAPITEL 4. THERMODYNAMIK
98
Entropienderung bei reversiblen und irreversiblen Kreisprozessen
Man ndet allgemein: Bei reversiblen Prozessen ist S = 0.
Beweis:
Jeder Kreisproze lt sich durch berlagerung unendlich vieler innitesimal kleiner
Carnot - Prozesse darstellen.
Ferner gilt: Bei irreversiblen Kreisprozessen nimmt die Entropie zu, d.h. S > 0.
4.7.4 Nullpunkt der Entropie und dritter Hauptsatz
Bis jetzt: immer Berechnung von S, nicht aber von S.
Dritter Hauptsatz der Thermodynamik
Am absoluten Nullpunkt ist die Entropie = 0:
T = 0 ,T S = 0 T
R
R
Mit S(t) = dQTmax = cTv dT fT ! 0g ! 0
0
0
folgt:
cv ! 0 fr T! 0, wobei cv : Wrmekapazitt bei konstantem Volumen
) Es ist prinzipiell unm
glich, den absoluten Temperaturnullpunkt zu erreichen.
4.7.5 Der berstrmversuch von Gay - Lussac
Das Experiment
01
1010
10
1010
1010
1010
000000000
111111111
111111111
000000000
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
V1
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
ideales Gas
Trennwand wird herausgezogen
V2
Vakuum
Ziehen der Trennwand ) Gas str
mt ohne Verrichtung von Arbeit und ohne
Wrmeaustausch mit der Umgebung in V1.
vorher: V = V1
nachher: V = V1 + V2
Die Entropienderung beim berstrmversuch
S = TQ mit Q = 0: daraus folgt nicht S = 0, da es sich hier oensichtlich
um einen irreversiblen Proze handelt.
Wie berechne ich S bei irreversiblen Prozessen?
4.7. ENTROPIE UND DER ZWEITE HAUPTSATZ
99
Trick: Entropie ist Zustandsgr
e ) S ist nur vom Anfangs - und Endzustand
abhngig, nicht aber vom Weg.
Ich denke mir einen Weg von Zustand (1) nach Zustand (2), der nur aus reversiblen
Prozessen besteht.
R
) Jetzt kann ich S ganz normal berechnen: S = dQ
T
Konkret am Beispiel des berstr
mversuches: Betrachte isotherme Expansion (reversibel) von V1 auf
(V1 + V2 ):
01
10
1010
1010
1010
1010
10
111111111
000000000
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
V1
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
V2
dV
V
dS = dQTrev = dU +T pdV = p + nRT
T
R
V
+
V
V1+V2
)S = nR V11 2 dV
V = nR ln( V2 )
= N kln( V1V+2V2 )
Entropie und Wahrscheinlichkeit
V1
11
00
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
00
11
V2
vorher: alle Teilchen in V2
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
nachher: Teilchen in V1 und V2
Wahrscheinlichkeit, ein Teilchen in V1 zu nden:
100
KAPITEL 4. THERMODYNAMIK
w1(V1 ) = V1V+1V2
Wahrscheinlichkeit, alle N Teilchen in V1 zu nden:
wN (V1 ) = ( V1V+1V2 )N
Wahrscheinlichkeit, alle N Teilchen in V1 + V2 zu nden:
wN (V1 + V2 ) = 1
) S = kln(w)
Entropie hat mit der statistischen Wahrscheinlichkeit eines Zustandes und damit
mit der Zahl seiner Realisierungsm
glichkeiten zu tun.
T=0,S=0
(dritter Hauptsatz)
) nur noch eine Realisierungsm
glichkeit bei T = 0. Das System nhme bei
T = 0 (wenn diese Temperatur erreichbar wre) den perfekt geordneten Zustand
ein.
Aber was hat man dann von der ganzen Ordnung? : : :
Index
Adiabate, 90
Adiabatenkoe&zient, 88
quipartitionstheorem, 84
Aktionsprinzip, 14
Anzahldichte, 83
aperiodischer Grenzfall, 61
Arbeit, 31
allgemein, 20
Reibungs-, 17
Auftrieb, 47
Avogadro
Konstante, 81
Avogadro
Gesetz von, 81
Cavandish: Gravitationsdrehwaage, 40
Corioliskraft, 15
Daltonsches Partialdruckgesetz, 85
Dampfdruck, 85
Dehnung, 43
Dierentialgleichung, 58
Dispersion, 76
Dopplereekt, 75
Drehbewegung, 17
Drehimpuls, 29, 31
Drehimpulserhaltungssatz, 31
Drehmoment, 30, 31, 35
Drehschwingung, 59
Druck
Flssigkeitskugel, 49
isotroper, 44
Schwere-, 52
Seifenblase, 50
Stau-, 52
Barometrische H
henformel, 48
Bernoulli-Gleichung, 52
Beschleunigung, 31
allgemein, 11
mittlere, 10
momentane, 10
radial, 18
Winkel-, 31
bewegte Quelle, 75
bewegter Beobachter, 76
Bewegung
gleichf
rmig beschleunigte, 11
Bewegungsgleichung, 58
Bezugssystem, 14
gleichf
rmig rotierendes, 19
Bindungsenergie, 39
Binnendruck, 86
Boltzmann - Konstante, 82
Boltzmann- Faktor, 84
Boyle-Mariotte, 82
E-Modul, 43
Einheitsvektor, 18
Einschwingvorgnge, 63
Elastizittsgrenze, 42
Elastizittsmodul, 43
Elementarwelle, 73
Ende
geschlossenes, 73
oenes, 73
Energie
elastische, 46
innere, 87
kinetische, 23, 31
der Rotation, 29
potentielle, 21
Energiedichte
Carnot, 91
101
INDEX
102
fr Dehnung, 46
fr Torsion, 46
Energieerhaltungssatz (EES), 23
Energiestromdichte, 75
Energietransport durch die Welle, 75
Entropie, 97
Nullpunkt, 98
Entropienderung, 98
Expansion, 90
Feder
Hook'sche, 59
Federkonstante, 15
Federkonstante
eines Stabes, 46
Federwaage, 15
fest, 79
Festigkeitsgrenze, 42
Figurenachse, 36
Fluchtgeschwindigkeit, 41
ssig, 79
Flssigkeitsthermometer, 79
Flulinien, 50
Fourier
Analyse, 67
Koe&zienten, 67
Spektrum, 67
Synthese, 67
freie Achsen, 36
freier Fall, 12
Freiheitsgrade, 84, 88
Fundamentalschwingungen, 68
Gase
ideale, 81
reale, 81, 86
gasf
rmig, 80
Gasgleichung, ideale, 82
Gastheorie
kinetische, 83
Gasverssigung, 86
Gay - Lussac
berstr
mversuch, 98
Gay-Lussac
Gesetz von, 82
Gegenkraft, 16
Geschwindigkeit, 31
mittlere, 9
momentane, 9
Winkel-, 31
Gleichverteilungssatz, 84
Gleitreibungskraft, 16
Gradient, 24
Gravitationsfeldstrke, 39
Gravitationskonstante, 39
Gravitationspotential, 39
Grenzfall
aperiodisch, 61
griechische Buchstaben, 8
Gruppengeschwindigkeit, 76
Haftreibungskonstante, 17
Haftreibungskraft, 16
Hagen-Poiseuille, Gesetz von, 54
harmonischer Oszillator, 59
Hauptsatz
dritter, 98
erster, 87
nullter, 77
zweiter, 96
Haupttrgheitsachsen, 35, 36
Hebelgesetz, 30
Heiluftmotor, 95
Hook'sche Feder, 59
Hooksches Gesetz der Torsion, 38
Hooksches Gesetz, 15, 25, 43
Huygenssche
Elementarwelle, 73
Prinzip, 72
Impuls, 15, 31
Impulserhaltungssatz, 26
Inertialsystem, 14
Interferenz
destruktiv, 76
konstruktiv, 76
Isentropen, 97
INDEX
Joule - Thomson
Eekt von, 86
Kapillardruck, 50
Kapillaritt, 50
Kelvin, absolute Temperatur, 78
Keplersches Gesetz
1., 40
2., 40
3., 40
Kernladungszahl, 81
Kohrenz, 76
Kompressibilitt, 44
Kompression, 90
Kompressionsmodul, 44
Kondensationswrme, 80
Kontinuittsgleichung, 51
Kopplung
schwache, 69
Kraft, 15
elastische, 24
konservative, 23
nicht-konservative, 23
Tangential-, 30
Kraftkonstante, 31
Kreisbewegung, 18
Kreisel, 35
Kreisfrequenz, 18, 25
Kreisproze, 91
Kriechfall, 61
Khlschrank, 94, 95
Lngenausdehnung, 78
Leistung, 21, 31
der Rotation, 29
mechanische, 21
Linde Verfahren, 86
Lissajous Figur, 66
Luftfeuchtigkeit, 85
relative, 85
Masse, 15
schwere, 16
trge, 16
103
Masse der Erde, 40
Massenmittelpunkt, 26
Massentrgheitsmoment, 31
Massenzahl, 81
mathemathisches Pendel, 59
Maxwellsche Geschwindigkeitsverteilung,
84
mol, 81
Molwrmen, spezische, 87
Newtonsches Axiom
1., 14
2., 14
3., 14
Newtonsches Reibungsgesetz, 53
Normalkraft, 17
Nutation, 36
Oberchenspannung, 49
Oszillator
gedmpft, 60
harmonisch, 59
Partialdruck, 85
Pascalsches Prinzip, 46
Pendel
mathematisch, 59
physikalisch, 60
Perpetuum Mobile, 23
Phasengeschwindigkeit, 72
Phasensprung, 73
Phasenumwandlungen, 79
physikalisches Pendel, 60
Pitol-Rohr, 52
Poisson-Zahl, 43
Potential, 23
Przession, 37
Prandelsches Staurohr, 52
Prinzip von Archimedes, 48
Proportionalittsgrenze, 42
Prozesse
adiabatische, 90
irreversible, 97
isobare, 89
INDEX
104
isochore, 88
isotherme, 89
polytrope, 90
reversible, 97
Querkontraktion, 43
Radialbeschleunigung, 19
Reaktionsprinzip, 14
Rechtssystem, 18
Reibungskrfte, 16
Reigrenze, 42
Resonanz, 63
Resonanzfrequenz, 63, 73
Resonanzberh
hung, 63
Reynoldszahl, 54
Rollbedingung, 34
Rotation, 17, 29
Rckstellkraft, 49
Satellitenbahnen, 41
Satz von Steiner, 34
Scheinkrfte, 19
Schermodul, 44
Scherspannung, 44
Scherung, 44
Schmelzwrme, 79
Schwebung
rein, 64
unrein, 64
Schweredruck, 47, 50
Schwerelosigkeit, 16
Schwerpunkt, 26
Schwingfall, 60
Schwingung
harmonische, 24
einer Hookschen Feder, 25
Energieerhaltung, 25
Schwingungen, 57
Dreh- , 59
erzwungen, 62
gegenphasig, 68
gekoppelt, 67
gleichphasig, 68
harmonisch, 58, 59
inharmonisch, 58
berlagerung, 63
orthogonal, 65
parallel, 63
Schwingungsbauch, 73
Schwingungsknoten, 73
Siedepunkt, 85
Skalarprodukt, 21
Spannarbeit, 31
Stirling - Proze, 95
Stomenge, 81
Stokes-Gesetz, 60
Stokesches Gesetz, 54
Sto
elastischer, 27
gerader, zentraler, 27
gerader, zentraler inelastischer, 27
Strahlungspyrometer, 79
Str
mung
stationre, 50
Str
mung
laminare, 54
turbulente, 54
viskose, 53
Superpositionsprinzip, 12
Symmetrieachse, 36
Taupunkt, 85
Temperatur, 77
Thermoelemente, 79
Thomson, 86
Torsion, 45
Torsionskonstante, 45
Torsionsmodul, 44
Trgheitsmoment, 29, 32
Trgheitsprinzip, 14
Translation, 29
berstr
mversuch, 98
Umlaufzeit, 18
universelle Gaskonstante, 82
van der Waals, 86
INDEX
Vektor
axialer, 18
Vektorprodukt, 18
Verdampfungswrme, 80
Verformung
elastische, 42
plastische, 42
Viskositt, 53
Volumenausdehnung, 79
waagrechter Wurf, 12
Waals
van der, 86
Wrme
latente, 79
spezische, 79
Wrmeausdehnungskoe&zient, 79
Wrmeenergie, 77, 79
Wrmepumpe, 95
Wasser, 80
Wasser
Dichteanomalie, 81
Weg, 31
Wellen, 71
ebene, 72
gegenphasig, 76
gleichphasig, 76
Kreis-, 72
Kugel-, 72
longitudinale, 72
stehende, 73
transversale, 72
Wellenarten, 72
Wellenfront, 72
Wellengleichung, 72
Wellenlnge, 71
Wellenzahl, 71
Widerstandsthermometer, 79
Winkel, 29, 31
Winkelbeschleunigung, 19, 29
Winkelgeschwindigkeit, 18, 29
Winkelrichtgr
e, 31
Wirkungsgrad, 21, 93
105
Zehnerpotenzen, 8
Zugspannung, 43
Zustand
gebundener, 41
Zustand
ungebundener, 41
Zustandsnderung, 88
Zustandsgleichung, 82