Kapitel 2
Werbung

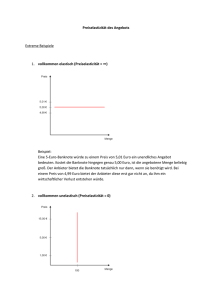
IK Ökonomische Entscheidungen & Märkte LVA-Leiter: Martin Halla Einheit 3 : Produzenten, Konsumenten & Wettbewerbsmärkte (Kapitel 2 - Teil II). IK Ökonomische Entscheidungen & Märkte Einheit 3 -1- Elastizität Die Elastizität E misst die Empfindlichkeit (Reagibilität) einer Variable (y) im Hinblick auf eine marginale Veränderung einer anderen Variable (x). 4y/y ∂y/y x ∂y E = lim = = · 4x→0 4x/x ∂x/x y ∂x • |E| < 1 unelastischer Zusammenhang • |E| = 1 isoelastischer Zusammenhang • |E| > 1 elastischer Zusammenhang IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 -2- Typen von Elastizitäten „Erweiterte Nachfragefunktion“: QD = QD (P, I, Pother )1 • Preiselastizität der Nachfrage EPD = P QD other ) · ∂QD (P,I,P ∂P • Einkommenselastizität der Nachfrage EID = I QD • Kreuzpreiselastizität der Nachfrage EPDother = • Preiselastizität des Angebotes EPS = 1 P QS other ) · ∂QD (P,I,P ∂I Pother QD (P,I,Pother ) · ∂QD∂P other S (P ) · ∂Q∂P P . . . Preis des betrachteten Gutes; I . . . Einkommen und Pother Preis des/r anderen Gutes/Güter. IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 -3- Preiselastizität der Nachfrage. • Preiselastizität der Nachfrage: Wie reagiert die nachgefragte Menge eines Gutes auf eine Preisänderung? EPD = P QD other ) · ∂QD (P,I,P ∂P EPD < 0 −→ gewöhnliches Gut EPD > 0 −→ Giffen Gut IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 -4- Einkommenselastizität der Nachfrage. • Einkommenselastizität der Nachfrage: Wie reagiert die nachgefragte Menge eines Gutes auf eine Änderung des Einkommens? EID = I QD other ) · ∂QD (P,I,P ∂I EID > 0 −→ normales Gut EID < 0 −→ inferiores Gut IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 -5- Kreuzpreiselastizität der Nachfrage. • Kreuzpreiselastizität der Nachfrage: Wie reagiert die nachgefragte Menge eines Gutes auf eine Änderung des Preises eines anderen Gutes? EPDother = Pother QD (P,I,Pother ) · ∂QD∂P other EPDother > 0 −→ Substitut EPDother < 0 −→ Komplement EPDother = 0 −→ abgegrenzte Märkte IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 -6- Preiselastizität des Angebots. • Preiselastizität des Angebots: Wie reagiert die angebotene Menge eines Gutes auf eine Preisänderung? EPS = P QS S (P ) · ∂Q∂P IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 -7- Berechnung der Preiselastizität der Nachfrage EPD P ∂QD (P ) = · QD ∂P Bsp.: QD (P ) = 8 − 4P EPD =? Einzelarbeit: 5 min IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 -8- Berechnung der Preiselastizität der Nachfrage EPD = Bsp.: QD (P ) = 8 − 4P, P ∂QD (P ) · QD ∂P QD ≡ Q P P = Q 8 − 4P ∂Q(P ) = Q0(P ) = −4 ∂P EPD P −P P ∂Q(P ) = · = · −4 = Q ∂P 8 − 4P 2−P bei z. B. P ∗ = 1 (siehe oben) beträgt EPD gleich − 1. IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 -9- Berechnung der Preiselastizität des Angebotes EPS P ∂QS (P ) = · QS ∂P Bsp.: QS (P ) = 2 + 2P EPS =? Einzelarbeit: 5 min IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 10 - Berechnung der Preiselastizität des Angebotes EPS = P ∂QS (P ) · QS ∂P QS ≡ Q Bsp.: QS (P ) = 2 + 2P, P P = Q 2 + 2P ∂Q(P ) = Q0(P ) = 2 ∂P EPS P ∂Q(P ) P 2P = · = ·2= Q ∂P 2 + 2P 2 + 2P bei z. B. P ∗ = 1 (siehe oben) beträgt EPS gleich 1/2. IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 11 - Berechnung der Einkommenselastizität der Nachfrage EID I ∂QD (P, I, Pother ) = · QD ∂I Bsp.: QD (P, I, Pother ) = 20 − 4P + 2I + Pother P =3 I=5 Pother = 2 EID =? Einzelarbeit: 5 min IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 12 - Berechnung der Einkommenselastizität der Nachfrage EID I ∂QD (P, I, Pother ) = · QD ∂I Bsp.: QD (P, I, Pother ) = 20 − 4P + 2I + Pother , P = 3, I = 5, Pother = 2, QD ≡ Q I I = Q 20 − 4P + 2I + Pother ∂Q(·) =2 ∂I EID I 5 = ·2= · 2 = 0, 5 20 − 4P + 2I + Pother 20 − 4 · 3 + 2 · 5 + 2 IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 13 - Berechnung der Kreuzpreiselastizität der Nachfrage EPDother Pother ∂QD (P, I, Pother ) = · QD ∂Pother Bsp.: QD (P, I) = 20 − 4P + 2I + Pother P =3 I=5 Pother = 2 EPDother =? Einzelarbeit: 5 min IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 14 - Berechnung der Kreuzpreiselastizität der Nachfrage EPDother = Pother ∂QD (P, I, Pother ) · QD ∂Pother Bsp.: QD (P, I) = 20 − 4P + 2I + Pother , P = 3, I = 5, Pother = 2, QD ≡ Q Pother Pother = Q 20 − 4P + 2I + Pother ∂Q(·) =1 ∂Pother EPDother Pother 2 = ·1= · 1 = 0, 1 20 − 4P + 2I + Pother 20 − 4 · 3 + 2 · 5 + 2 IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 15 - Preiselastizität der Nachfrage (graphisch) Abbildung 1: Preiselastizität der Nachfrage I IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 16 - Preiselastizität der Nachfrage (graphisch) Abbildung 2: Preiselastizität der Nachfrage II IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 17 - Preiselastizität der Nachfrage (graphisch) Abbildung 3: Preiselastizität der Nachfrage III IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 18 - Preiselastizitäten einer linearen Nachfragekurve Abbildung 4: Preiselastizität entlang einer linearen Nachfragefunktion IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 19 - Zeitliche Dimension der Elastizität Wieviel Zeit vergeht zwischen der Änderung der betrachteten Variable und der Messung? • Bei dauerhaften Konsumgütern (z. B.: PKW’s) ist die kurzfristige Elastizität der Nachfrage dem Betrag nach größer als die langfristige. • Bei kurzlebigen Konsumgütern (z. B.: Benzin) ist die kurzfristige Elastizität der Nachfrage dem Betrag nach kleiner als die langfristige. • Siehe Tabellen 2.1 & 2.2. • Angebotselastizitäten sind idR kurzfristig kleiner als langfristig. IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 20 - Staatliche Intervention. • Auf dem freien Wettbewerbsmarkt bestimmen Angebot und Nachfrage den Preis sowie die abgesetzte Menge eines Gutes. • Die Gesetze von Angebot und Nachfrage führen den freien Markt dabei ins Gleichgewicht, Angebots- oder Nachfrageüberschüsse treten nur temporär auf. • Wie verändert jedoch staatliche Intervention (wirtschaftspolitische Maßnahmen) diese Ergebnisse? IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 21 - Staatliche Intervention: Preisvorschriften. Der Staat hat z. .B. die Möglichkeit Preisvorschriften festzulegen: • Höchstpreis (price ceiling ): Gesetzlich vorgeschriebener Maximalpreis für ein Gut. • Mindestpreis (price floor ): Gesetzlich vorgeschriebener Minimalpreis für ein Gut. Beispiele: Mietpreisbindung, Preisgarantien (z. B. für Milch), Mindestlöhne, . . . IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 22 - Staatliche Intervention: Höchstpreis. Abbildung 5: Preisregulierung durch Höchstpreis. IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 23 - Staatliche Intervention: Mindestpreis. Abbildung 6: Preisregulierung durch Mindestpreis. IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 24 - Staatliche Intervention. • Höchstpreis P H < P ∗ −→ Überschussnachfrage! • Mindestpreis P M > P ∗ −→ Überschussangebot! =⇒ . . . Gewinner & Verlierer; Summe ≶ 0? • Höchstpreis P H > P ∗ −→ Gleichgewicht! • Mindestpreis P M < P ∗ −→ Gleichgewicht! =⇒ . . . kein Effekt. IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 25 - Mindestlöhne — ein Beispiel aus der Praxis. Abbildung 7: Die Wirkung eines bindenden Mindestlohnsatzes. IK Ökonomische Entscheidungen & Märkte c Martin Halla Einheit 3 - 26 - Marktinterventionen mittels Steuern. • Der Staat verfügt über ein weiteres wichtiges Instrument des Markteingriffes: Steuern. • Steuern verändern ähnlich wie Preiskontrollen ebenfalls die freien Marktergebnisse, wobei gilt: Preis der Verkäufer 6= Preis der Käufer • −→ KS & IK Economics IIb. IK Ökonomische Entscheidungen & Märkte c Martin Halla